
湛江海洋大学2005一一 2006学年第一学期 5.求序列x(m)=(n-3)的Z变换及其收敛域。 级 《数字信号处理》课考试(查)试题(A) 使用班级:电子1031-1036,通信1031-1036考试人数: 题 二三四 五六七八九十总分 阅卷教师 各题分数 4810121515 6.利用Z变换法求解差分方程描述系统的系统函数H(z)。 实得分数 n)-0.9n-1)=0.05u(n,tn)=0,n≤-1 姓名, (试卷内容采用4号宋体) 一、简单计算(每题6分,共计48分) 3 1.x(m)=3sin(号m- 5 是否为周期函数,如是请确定其最小 正周期。 7.写出图肿流图的系统函数表达式。 xn)→ y(n) 2.判断系统(n)=x(n)+2x(n-1)+3xr(n-2)是否为线性时不变。 ! 8.已知FIR滤波器的单位脉冲响应为:N=7,h()=[3,-2,1,0,1,-2,3】,说 3.已知线性时不变系统的单位取样响应h()和输入x(n),求输出(n)。 明其相位特性,求群时延。 加 4.已知序x(m)=R(n),求x(n)的8点DFT变换。 第 页共 页
第 页 共 页 湛江海洋大学 2005 —— 2006 学年第 一 学期 《 数字信号处理 》课考试(查)试题(A) 使用班级:电子 1031-1036,通信 1031-1036 考试人数: 题 号 一 二 三 四 五 六 七 八 九 十 总分 阅卷教师 各题分数 48 10 12 15 15 实得分数 (试卷内容采用 4 号宋体) 一、简单计算(每题 6 分,共计 48 分) 1. ) 5 5 3 ( ) 3sin( x n = n − 是否为周期函数,如是请确定其最小 正周期。 2.判断系统 y(n) = x(n) + 2x(n −1) + 3x(n − 2) 是否为线性时不变。 3.已知线性时不变系统的单位取样响应 h(n) 和输入 x(n) ,求输出 y(n)。 4.已知序 ( ) ( ) x n = R5 n ,求 x(n)的 8 点 DFT 变换。 5.求序列 x(n) = (n − 3) 的 Z 变换及其收敛域。 6.利用 Z 变换法求解差分方程描述系统的系统函数 H(z)。 y(n) − 0.9y(n −1) = 0.05u(n), y(n) = 0,n −1 7.写出图肿流图的系统函数表达式。 8.已知 FIR 滤波器的单位脉冲响应为:N=7,h(n)=[3,-2,1,0,1,-2,3] ,说 明其相位特性,求群时延。 班 级 : 姓 名 : 学 号 : 加 白 纸 张 密 封 线 y(n) 1/2 -8 3 1/4 x(n) 2 Z -1 Z -1 Z -1
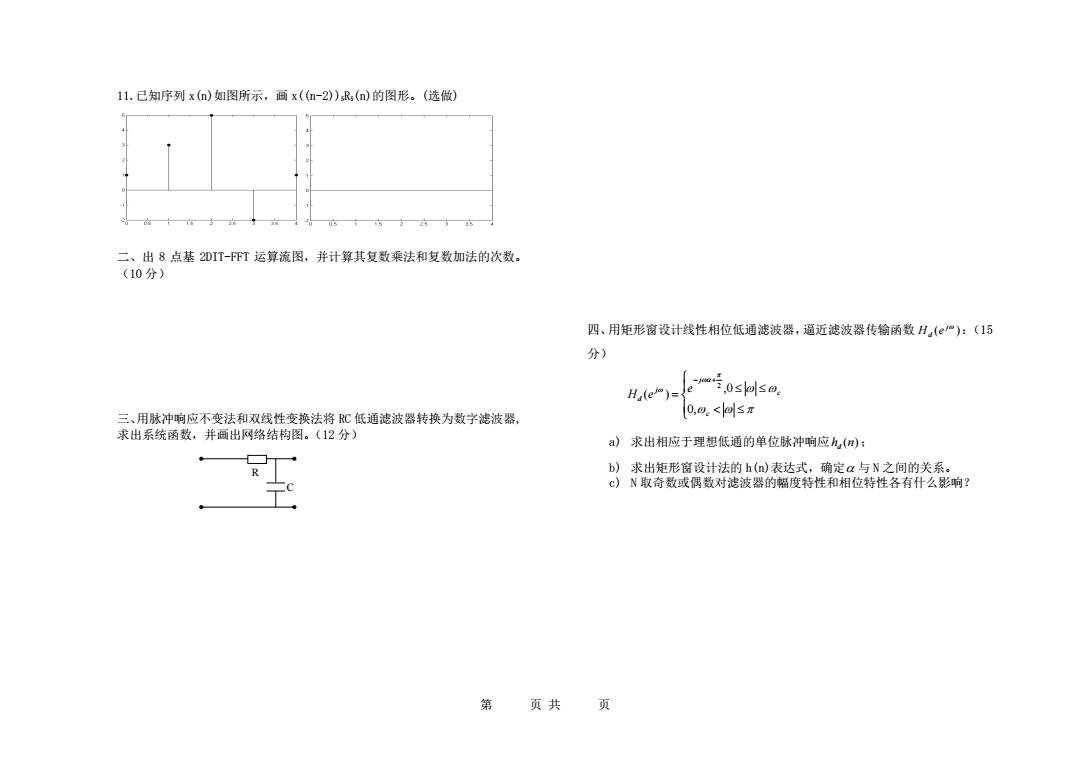
11.已知序列x()如图所示,画x(n-2))R(n)的图形。(选做) 二、出8点基2DIT-FFT运算流图,并计算其复数乘法和复数加法的次数。 (10分) 四、用矩形窗设计线性相位低通滤波器,逼近滤波器传输函数H(m):(15 分) H(e)= rm片0shl5o e 三、用脉冲响应不变法和双线性变换法将C低通滤波器转换为数字滤波器, 0,o.<o≤π 求出系统函数,并画出网络结构图。(12分) a)求出相应于理想低通的单位脉冲响应h(m): b)求出矩形窗设计法的h(n)表达式,确定a与N之间的关系。 C)N取奇数或偶数对滤波器的幅度特性和相位特性各有什么影响? 第 页共 页
第 页 共 页 11.已知序列 x(n)如图所示,画 x((n-2))5R5(n)的图形。(选做) 二、出 8 点基 2DIT-FFT 运算流图,并计算其复数乘法和复数加法的次数。 (10 分) 三、用脉冲响应不变法和双线性变换法将 RC 低通滤波器转换为数字滤波器, 求出系统函数,并画出网络结构图。(12 分) 四、用矩形窗设计线性相位低通滤波器,逼近滤波器传输函数 ( ) j d H e :(15 分) = − + c c j j d e H e 0, ,0 ( ) 2 a) 求出相应于理想低通的单位脉冲响应 h (n) d ; b) 求出矩形窗设计法的 h(n)表达式,确定 与 N 之间的关系。 c) N 取奇数或偶数对滤波器的幅度特性和相位特性各有什么影响? R C

五、己知序列x(m=1,2,3,4,2(m={1,11,1),求两个序列的线性卷积,和 N=5及N=7点的循环卷积。(15分) 第 页共 页
第 页 共 页 五、已知序列 ( ) {1,2,3,4} x1 n = , ( ) {1,1,1,1} x2 n = ,求两个序列的线性卷积,和 N=5 及 N=7 点的循环卷积。(15 分)