广东海洋大学：《数字信号处理 Digital Signal Processing》课程教学资源（作业习题）第四章 有限长单位脉冲响应滤波器的设计方法（习题及答案）

4.1 用矩形窗设计一线性相位高通滤波器 Ha(e/0)= eor)a,n-0。≤0≤π 0,其它 1)写出h(n)的表达式，确定a与N的关系 2)问有几种类型，分别是属于哪一种线性相位滤波器 其幅度特性： H(W) 1 π-0c π )

其幅度特性： 1 H(w)  w 4.1 ）问有几种类型，分别是属于哪一种线性相位滤波器 ）写出 的表达式，确定 与 的关系 其它 用矩形窗设计一线性相位高通滤波器 2 1 ( ) N 0, , H ( ) ( ) h n a e e c j a j d    −   = − −         −c

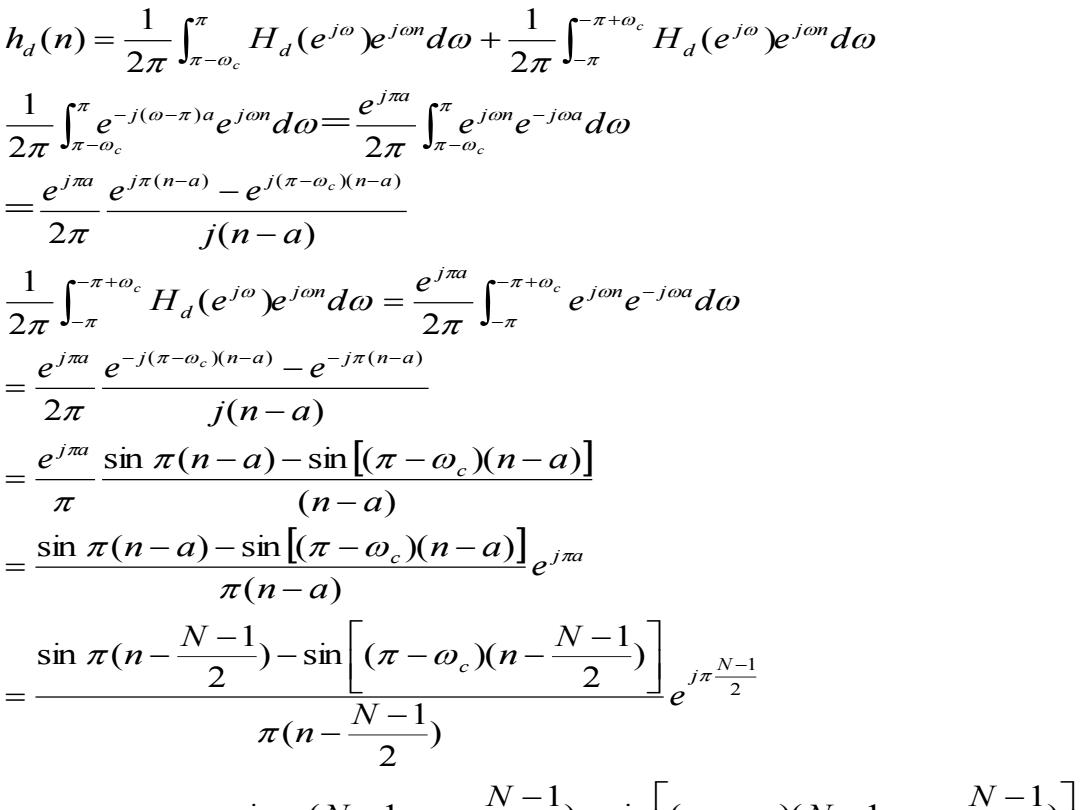
h.(m)=2n了nH,emed加+2nH,do 2元 2 gda=gea加 eln ein(n-a）-ej(π-wen-a) 2元 j(n-a) eim e-iπ-w.Xn-a）-ejπ(n-a） 2π j(n-a) eix sin a(n-a)-sin [(n-0)(n-a) π (n-a) sin (n-a）-sin[【(n-o)n-a】]em π(n-a) sh a(o-N-sm (r-m.Xn- 2 N-1 jπ 2 N-1 2 W-1、 W-1

    ( ) ( ) ( ) N 2 1 ) 2 1 ( ) 2 1 ) sin ( )( 2 1 sin ( ) 2 1 ( 1 ) 2 1 ) sin ( )( 1 2 1 sin ( 1 ( 1 ) ) 2 1 ( ) 2 1 ) sin ( )( 2 1 sin ( ( ) sin ( ) sin ( )( ) ( ) sin ( ) sin ( )( ) 2 ( ) 2 ( ) 2 1 2 ( ) 2 2 1 ( ) 2 1 ( ) 2 1 ( ) 2 1 2 1 2 1 ( )( ) ( ) ( ) ( )( ) ( ) h n h n w n N N a e N n N n N n e N N n N N n N N n h N n e N n N n N n e n a n a n a n a e n a n a j n a e e e e e d e H e e d j n a e e e e e d e e e d h n H e e d H e e d d N j c N j c d N j c c j a c j a j a j n a j n a j n j a j a j j n d j a j n a j n a j n j a j a j a j n j j n d j j n d d c c c c c c c c = − = − −       − − − − − − = − − − −       − − − − − − − − − − − − = − −       − − − − − − = − − − − − = − − − − − = − − = = − − = + − − − − − − − − − + − − − + − − − − − − − − − − + − −       为奇数时 为偶数时 ＝ ＝                                                                                

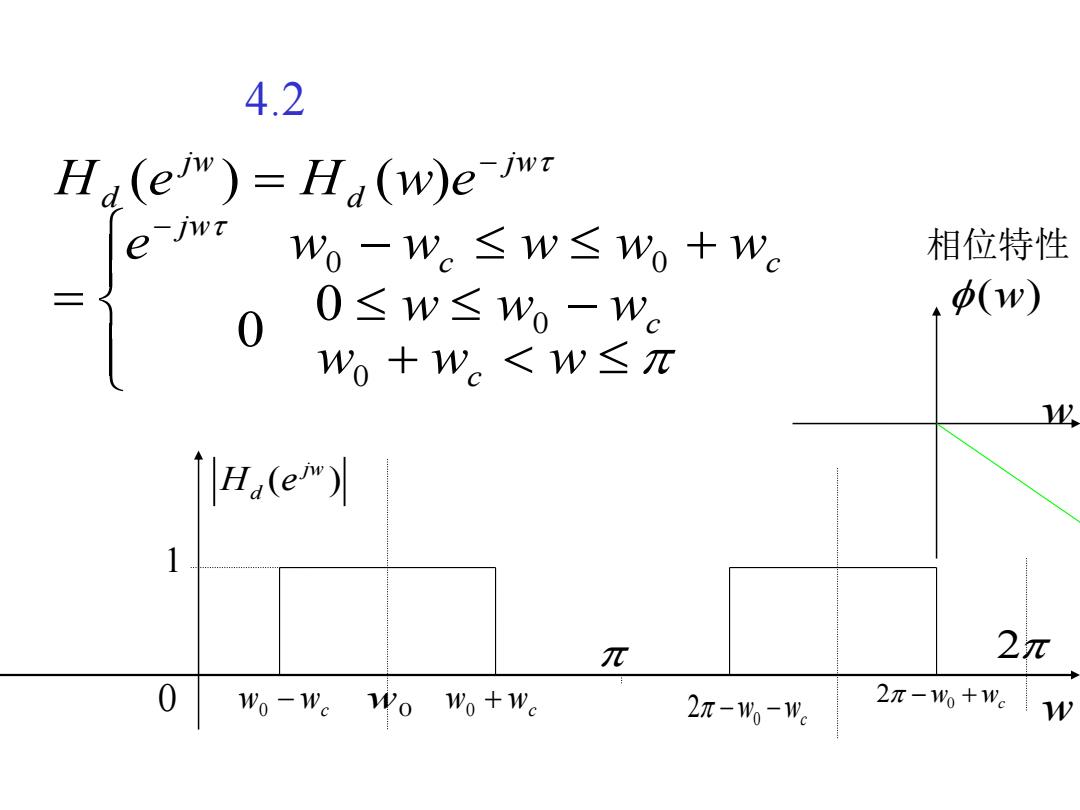
4.2 Ha(em)=Ha(w)eM -JwT Wo-We≤W≤Wo+We 相位特性 二 0≤w≤wo-wc (w) 0 Wo+W。<w≤π 业 H(e 1 元 2π M 0 W0-W。WoWo+Wc 2I-Wo-We 2π-w+w:W

    +     − −   + = = − −    w w w w w w e w w w w w H e H w e c c c c j w j w d j w d 0 0 0 0 0 0 ( ) ( ) (w) 相位特性 w 1 ( ) jw H e d w0 − wc w0 w0 + wc w  2 0 2 w wc 0  − − 0 2 − + w wc 4.2

,a）27,(eed 2ge加+2eemm 1 2n(n-t e wo-Wc 1 十 2(n-t) h() 2π-w0+we =2c0s(w(0m-x sin [we (n-)] 一oO<n<十0 π(n-t)

  −    + − − = − − + − = = + = − + − − − + − − − + − − − + − −    n n w n w n e j n e j n e e dw e e dw h n H e e dw c w w w w j w n w w w w j w n w w w w j w jwn w w w w j w jwn j w jwn d d c c c c c c c c ( ) sin ( ) 2cos( ( )) 2 ( ) 1 2 ( ) 1 2 1 2 1 ( ) 2 1 ( ) 0 2 2 ( ) ( ) 2 0 2 0 2 0 0 0 0 0 0 0 0 0                    

h(n)=ha(n)w(n) =2c0s(w,(n-t sin[w.(n-z)】 π(n-t) n=0,1,2,…N-1 sin [we(n-t) =偶函数 π(n-t) 又W(n)为偶数 ∴.h(n)即为偶对称，h(n)=h(N-1-n) .当N为奇数时， 对应于第一种线性相位带通FR 当N为偶数时， 设计是第二种线性相位带通DF

    DF N FIR N h n h n h N n W n n w n n N n w n w n h n h n W n c c d 设计是第二种线性相位带通 当 为偶数时， 对应于第一种线性相位带通 当 为奇数时， 即为偶对称， 又 为偶数 偶函数   = − − = − − = − − − = − = ( ) ( ) ( 1 ) ( ) ( ) sin ( ) 0,1,2, 1 ( ) sin ( ) 2cos( ( )) ( ) ( ) ( ) 0          

4.4 如果一个线性相位带通滤波器的频率响 应为： Hep(e)=HBp(@)eo) ● ·(1)试证明一个线性相位带阻滤波器可以 表示成 HpR(e)=1-HBp(@)]ei()

4.4 • 如果一个线性相位带通滤波器的频率响 应为： • • (1)试证明一个线性相位带阻滤波器可以 表示成 • ( ) ( ) ( )     j BP j BP H e = H e   ( ) ( ) 1 ( )     j BP j BR H e = − H e

(1)证明： 由于Hp(e)=HBp(o)eo(o),且又是一 线性相位带通滤波器，则： 0,0≤0<0-0.或 HBp(@)= 00+0。<0≤π 1，-0。≤0-00≤0c 且0(o)也是线性相位 1,0≤0<00-0。或 又因为H(eo)=HBR(o)epo）Hm(o)= 00+0。<0≤π 0 ,-0。≤0-00≤0c 因而HBR(O)=1-HBP(D) ·所以带阻滤波器可以表示成： ● HBR(e)=[1-Hpp(@)leio(o)

• • • 所以带阻滤波器可以表示成： • • • 线性相位带通滤波器，则： 由于 且又是一 证明： ( ) ( ) , (1) ( )     j BP j BP H e = H e      −  −  +     − = c c c c HBP             0 0 0 1 , 0 , 0 ( ) 或 且（）也是线性相位 ( ) 又因为 ( ) ( )     j BR j BR H e = H e      −  −  +     − = c c c c HBR             0 0 0 0 , 1 , 0 ( ) 或 () 1 () 因而 HBR = − HBP   ( ) ( ) 1 ( )     j BP j BR H e = − H e

4.6 1,k=0 Hk=0.5,k=1,14 0,2≤k≤13 求采样值的相位e()，并写出及的表达式H(eo)h(r)。 9)=--1o)=-N-1.2rk=- 4r.k 2 2 N 1 14还元 H(k)=Hxe0()=Hxe 15

求采样值的相位 ，并写出 及 的表达式 。 4.6        = = = 0,2 13 0.5, 1,14 1, 0 k k k Hk

h(n)= N k=0 14 15 k=0 15 1网借-列 e2 1-e-joN N k=0 1-eNe-jo 5m2} 0.5 0.5 sin(

          − + −  +      = − − =             = + −       = + +       = = + + = = − − = − − − − − − − = − − = = −     ) 15 14 2 sin( 0.5 ) 2 15 sin( 0.5 ) 2 sin( 1 2 15 sin 15 1 1 1 ( ) 1 ( ) ( 7) 15 2 1 cos 15 1 1 0.5[ ] 15 1 1 0.5 0.5 15 1 15 1 15 1 ( ) 1 ( ) 7 1 0 2 ( 7) 1 5 2 ( 7) 1 5 2 1 4( 7) 1 5 2 ( 7) 1 5 1 4 2 0 ( 7) 1 5 2 1 0 1 4 0 1 5 2 1 5 2 1 4                     j N k N j k j j N j j n j n j n j n k j k n k N k k j ke j kn k kn N j e e e e H k N H e n e e H e e e H k e H e e N h n

4.7 己知图1中的是偶对称序列，图2中的是圆 周移位后的序列。设 N=8,移位数为4，H(k)=DFT[h(n小，H,(k)=DFT[h(n)] 1)H,(k)=H2(k)成立吗？O(k)与0，(k)有何关系？ 2)h(n),h,(n)作为单位脉冲响应，可构成两个低通滤波器，是 3)这两种滤波器的性能是否相同？比较之

4.7 已知图1中的是偶对称序列，图2中的是圆 周移位后的序列。设 ）这两种滤波器的性能是否相同？比较之。 ） 作为单位脉冲响应，可构成两个低通滤波器，是否是线性相位滤波器？时延多少？ 成立吗？ （ 与 （ 有何关系？ 移位数为 ， 3 2 ( ), ( ) 1) ( ) ( ) ) ) 8, 4 ( ) [ ( )], ( ) [ ( )] 1 2 1 2 1 2 1 1 2 2 h n h n H k H k k k N H k DFT h n H k DFT h n =   = = =