
Chapter 5 载波和符号同步
Chapter 5 载波和符号同步

基本概念 为什么要进行载波和符号同步? ●接收端为了恢复发送信息,要对解调器输出周期性抽样。 但接收机对信号的传播时延未知,必须从接收信号中导出符号定时; ●如果采用相干检测,接收机必须估计载波相位的偏移。 精确相位估计的重要性: 例:考查DSB-SC信号 s(t)=A(t)cos(2gt+φ) 接收机参考载波 c(t)cos(2+) 解调器: c0a0=40eos0-+340co41+0- 低通滤波器输出: y0=7A)cos(0-) 相位误差中- 的影响: 以因子cos(-) 降低信号电压 ●以因子cos(-)降低信号功率 10°→功率损失0.13dB 2 30°→功率损失1.25dB
2 基本概念 为什么要进行载波和符号同步 ? ⚫接收端为了恢复发送信息,要对解调器输出周期性抽样。 精确相位估计的重要性: 例:考查DSB-SC信号 接收机参考载波 低通滤波器输出: s(t) = A(t) cos(2f t +) c ) ˆ c(t) = cos(2f c t + ) ˆ ( ) cos(4 2 1 ) ˆ ( )cos( 2 1 c(t)s(t) = A t − + A t f c t + − ) ˆ ( )cos( 2 1 y(t) = A t − 相位误差 − ˆ 的影响: ) ˆ cos( − ) ˆ cos ( 2 − 10o→功率损失0.13dB 30o→功率损失1.25dB ⚫以因子 降低信号电压 ⚫以因子 降低信号功率 但接收机对信号的传播时延未知,必须从接收信号中导出符号定时; ⚫如果采用相干检测,接收机必须估计载波相位的偏移。 解调器:

基本概念 例:QAM和M-PSK信号解调的情况 发送信号: s(t)=A(t)cos(2ft+)-B(t)sin(2+) 接收机解调的正交载波:c.()=cos(2t+) c(t)=-sin(2t+) 解调:(经低通滤波器处理后) 同相支路 y,()=A(t)cos()-B()sin( 正交支路 ()=B()cos)sin( 结论: ●在QAM和M-PSK中,相位误差的影响比PAM信号严重; ●不仅使信号功率减少因子c0$(中一),而且同相和正交支路 之间存在着交互干扰
3 例:QAM和M-PSK信号解调的情况 发送信号: 接收机解调的正交载波: 解调:(经低通滤波器处理后) 同相支路 正交支路 s(t) = A(t) cos(2f t +) − B(t)sin(2f t +) c c ) ˆ cc (t) = cos(2f c t + ) ˆ cs (t) = −sin(2f c t + ) ˆ ( )sin( 2 1 ) ˆ ( ) cos( 2 1 yI (t) = A t − − B t − 结论: ⚫在QAM和M-PSK中,相位误差的影响比PAM信号严重; ⚫不仅使信号功率减少因子 ,而且同相和正交支路 之间存在着交互干扰。 ) ˆ cos ( 2 − ) ˆ ( )sin( 2 1 ) ˆ ( )cos( 2 1 y (t) = B t − + A t − 基本概念

5.1信号参数估计 4
4 5.1 信号参数估计

信号参数估计 载波和符号同步中要估计的信号参数 发送信号 s(t)=Res,(t)e 信号经过高斯噪声信道,并产生x的延迟。 接收信号 r(t)=s(t-t)+n(t) =Re[s,(t-r)e+]e 传播延迟引起的载波相位 0=-2πft 实际中,中除了受x的影响外,还要受到其他因素的影响! 为了解调和相干检测,必须估计两个参数:T, 将接收信号表示为: (t)=s(t,,T)+n(t) ,令0代表向量{中,} 则: s(t,p,t)→s(t,0) 5
5 2 ( ) Re ( ) j f t l s t s t e = π c 2 ( ) ( ) ( ) Re ( ) ( ) j j f t l r t s t n t s t e z t e = − + = − + π c = −2 f c 载波和符号同步中要估计的信号参数 发送信号 接收信号 传播延迟引起的载波相位 为了解调和相干检测,必须估计两个参数:τ, 信号经过高斯噪声信道,并产生 的延迟。 将接收信号表示为: , 令 代表向量 {, } s t s t ( , , ) ( , ) → r(t) = s(t, , ) + n(t) 则: 信号参数估计 实际中, 除了受 的影响外,还要受到其他因素的影响!
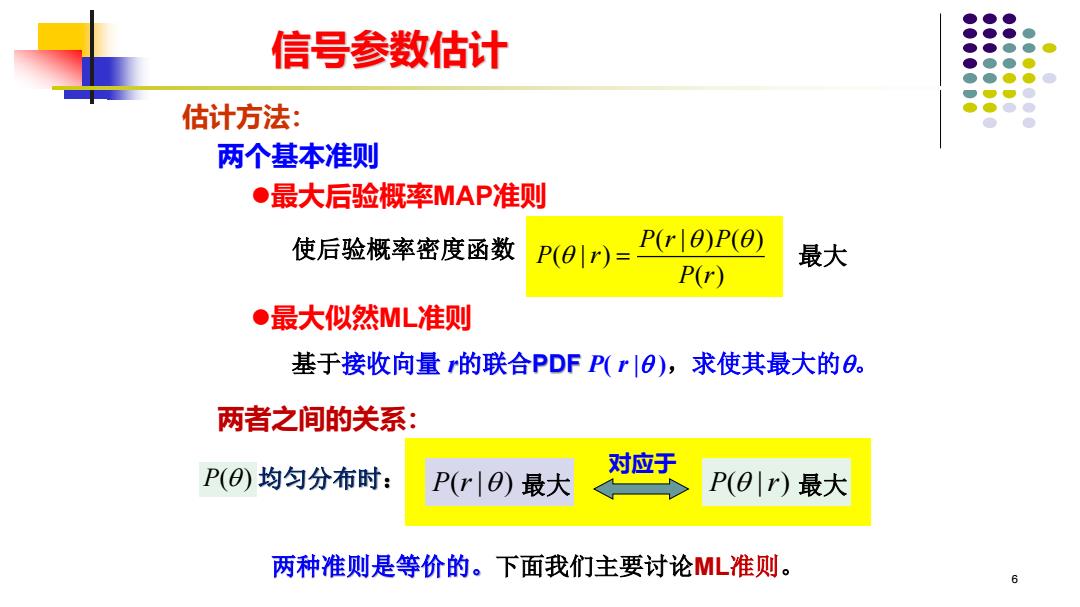
信号参数估计 估计方法: 两个基本准则 ●最大后验概率MAP准则 使后验概率密度函数 P(01r)= P(r 0)P(0) 最大 P(r) ●最大似然ML准则 基于接收向量r的联合PDFP(r|O),求使其最大的O。 两者之间的关系: P()均匀分布时: 对应于 P(r|O)最大 P(0r)最大 两种准则是等价的。下面我们主要讨论ML准则。 6
6 估计方法: 两个基本准则 ⚫最大似然ML准则 ⚫最大后验概率MAP准则 ( | ) ( ) ( | ) ( ) P r P P r P r 使后验概率密度函数 = 最大 P( ) 均匀分布时: P r( | ) 最大 P r ( | ) 最大 对应于 基于接收向量 r的联合PDF P( r | ),求使其最大的。 两者之间的关系: 两种准则是等价的。下面我们主要讨论ML准则。 信号参数估计

信号参数估计 如何获得似然函数,并导出参数估计值? (两条途径) N个标准正 ●由(①的展开式 交函数}根据r代)展开式随机变量[1,r2,…r] 的联合PDF来导出; ●直接处理接收信号波形,从P(r8)的连续时间等效形式中导出. 接收信号: r(t)=s(t,θ)+n(t) 向量表示:r=[,,LLw】 =s,(0)+n n:零均值高 斯白噪声 r的联合PDF: P(r10)= (n-sn(0)月 exp 2o2 其中:=Jr()(0d s(0)=s(t,(1)di 指数项的自变量: m2a2-uJro)-k,o明rdh (用信号波形)和s(t,表示) 7 o2=N/2
7 如何获得似然函数 ,并导出参数估计值? (两条途径) 信号参数估计 ⚫由 r(t) 的展开式 根据r(t)展开式随机变量 [r1 , r2 , … rN ] 的联合PDF来导出; ⚫直接处理接收信号波形,从P(r | )的连续时间等效形式中导出. 0 ( ) ( , ) ( ) n n T s s t t dt = 0 ( ) ( ) n n T r r t t dt = 接收信号: 向量表示: 其中: ( ) n n r s n = + r t s t n t ( ) ( , ) ( ) = + n:零均值高 斯白噪声 2 2 1 1 ( ( )) ( | ) exp 2 2 N N n n n r s P r = − = − r的联合PDF: 指数项的自变量: 0 2 2 2 1 0 1 1 lim [ ( , )] [ ( ) ( , )] 2 N n n N n T r s t r t s t dt N → = − = − (用信号波形r(t)和s(t,)表示) 2 0 = N / 2 1 2 [ , , ] N r r r r = L L N个标准正 交函数{n (t)}

信号参数估计 定义:似然函数 A(0)=exp rwor P(rB)关于信号参数0的最大化问题: P(r)最大 等价于 似然函数人(0) 最大 后面将根据A(B)最大的观点研究参数估计。 估计的参数为:O→{攻} 8
8 似然函数 0 2 0 1 ( ) exp [ ( ) ( , )] T r t s t dt N = − − P r( | ) 最大 似然函数 ( ) 最大 等价于 定义: 信号参数估计 P(r| ) 关于信号参数 的最大化问题: 后面将根据( )最大的观点研究参数估计。 估计的参数为: → { , }
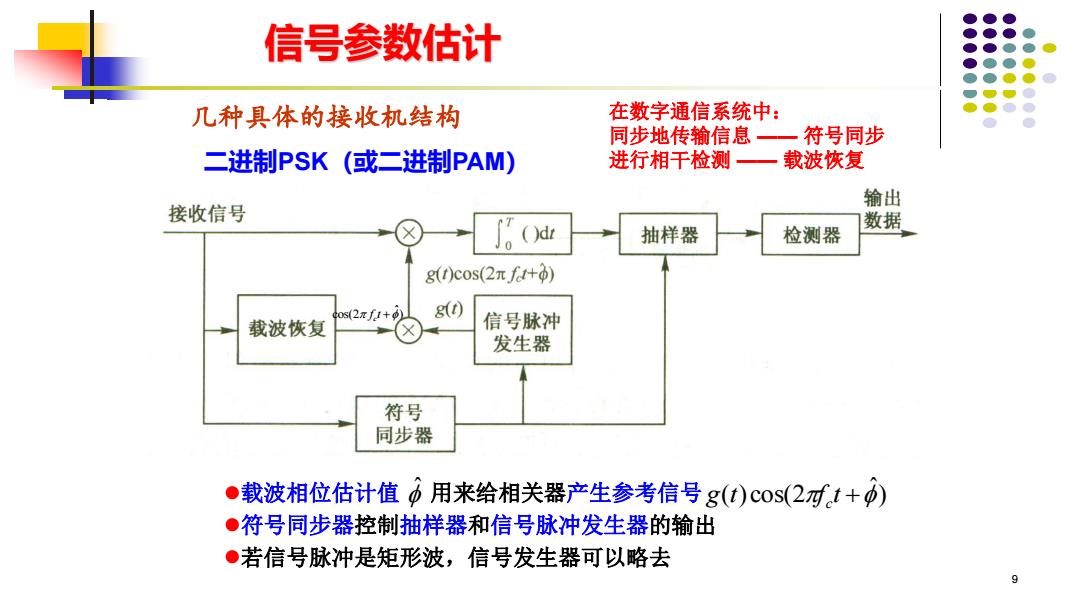
信号参数估计 几种具体的接收机结构 在数字通信系统中: 同步地传输信息—一 符号同步 二进制PSK(或二进制PAM) 进行相干检测—载波恢复 输出 接收信号 ()d 抽样器 检测器 数据 gt)cos(2πf+) 0s(2πf1+ 载波恢复 信号脉冲 发生器 符号 同步器 ●载波相位估计值中用来给相关器产生参考信号g(t)cos(2减t+) ●符号同步器控制抽样器和信号脉冲发生器的输出 ●若信号脉冲是矩形波,信号发生器可以略去 9
9 几种具体的接收机结构 二进制PSK(或二进制PAM) ⚫载波相位估计值 用来给相关器产生参考信号 ⚫符号同步器控制抽样器和信号脉冲发生器的输出 ⚫若信号脉冲是矩形波,信号发生器可以略去 ) ˆ g(t)cos(2f c t + ˆ 信号参数估计 ˆ cos(2 ) c f t + 在数字通信系统中: 同步地传输信息 —— 符号同步 进行相干检测 —— 载波恢复

信号参数估计 M元PSK接收机的方框图 抽样器 c0s(2πf+) 符号 同步器 收 输出 信号 载波恢复 信号脉冲 相位检测 数据 发生器 90° 相移 -sin(2πf+) (灿 抽样器 ●用两个相关器使接收信号与两个正交载波相关 ●检测器是一个相位检测器,它将接收信号相位与可能的发送信号相 位进行比较。 10
10 M元PSK接收机的方框图 ⚫用两个相关器使接收信号与两个正交载波相关 ⚫检测器是一个相位检测器,它将接收信号相位与可能的发送信号相 位进行比较。 信号参数估计