
4.5.3正交信号传输非相干检测 的错误概率 1
1 4.5.3 正交信号传输非相干检测 的错误概率

不确定情况下的最佳检测:非相干检测 M元正交信号包络检测的错误概率 假设:M个信号先验等概、等能量,在0≤tsT内发送信号为s0 判决度量:M个包络 12c 对应于发送信号s) hs=√g,sin中+ns 对应于其余信号sm() Ime =Nme m=2,3K M {nm,{nm}:相互独立的高斯随机变量 每个相关解调器输出的PDF:(前面推导的结果) Pr (nc,s)= oz expl- ++48 2元G 2o2 问题: Pn(Cmc,e)= 2zo2 exp[-. mc +r2 m=2,3K M 包络分布 2o2 的概率? 2
2 不确定情况下的最佳检测:非相干检测 2 2 m mc ms r = r + r = + = + s s s c s c r n r n 1 1 1 1 sin cos 2,3 mc mc ms ms r n m M r n = = = K 1 2 2 2 2 2 1 1 1 1 1 1 0 2 2 2 1 4 ( ) ( , ) exp[ ] [ ] 2 2 c s s s c s r c s r r r r P r r I + + + = − 2 2 2 2 1 ( , ) exp[ ] 2,3 2 2 m mc ms r mc ms r r P r r m M + = − = K 判决度量:M个包络 对应于发送信号s1 (t) 对应于其余信号sm(t) 每个相关解调器输出的PDF:(前面推导的结果) M元正交信号包络检测的错误概率 假设:M个信号先验等概、等能量,在0≤t≤T内发送信号为 s1 (t) {nmc}, {nms}:相互独立的高斯随机变量 问题: 包络分布 的概率?

不确定情况下的最佳检测:非相干检测 变量代换 +r2 Rm= mc s 0 Ime =oRm cosem → tan-I Tios rms =oRm sin em rRa)-会p-G+风1 2 PR,0.)=exp(-2R)) 2元 将变换后的P(RmOm)在日n上平均,即得到r包络的PDF ●R1具有Rice分布, ●Rm(m=2,3,.M)中的每一个都具有Rayleigl分布 3
3 不确定情况下的最佳检测:非相干检测 ms m m mc m m mc ms m mc ms m r R r R r r r r R sin cos tan 1 2 2 = = = + = − 变量代换 1 2 1 1 1 0 1 0 0 2 1 2 2 ( , ) exp[ ( )] [ ] 2 2 1 ( , ) exp( ) 2 2 s s m m m m R P R R I R N N R P R R = − + = − ⚫R1 具有Rice分布, ⚫Rm(m = 2, 3, … M)中的每一个都具有Rayleigh分布 将变换后的 P(Rm, m) 在m 上平均,即得到 r 包络的PDF

不确定情况下的最佳检测:非相干检测 正确判决概率(发送信号为s1()时): P=P(R<R,R3<R,K,Ry<R) -fP(R:<R.R<R.K,Rw<RIR;=x)pr.(x)dk Rm统计独立同分布,联合概率等于M-1个边缘概率的乘积 P.=S[P(R<RIR=x)]M-Pr(x)dk 由于P(R<RIR=x)=PG)d=1-ea 0-eay-3-yfn -exp[- nE (n+1)No E,/N一符号SNR 4
4 不确定情况下的最佳检测:非相干检测 1 2 1 3 1 1 1 0 ( , , , | ) ( ) P R R R R R R R x p x dx M R = = K 正确判决概率(发送信号为 s1 (t) 时): 1 1 2 1 1 0 [ ( | )] ( ) M P P R R R x p x dx c R − = = 2 2 / 2 2 1 1 2 2 0 ( | ) ( ) 1 x x P R R R x P r dr e R − = = = − − = − − − − − = − 1 0 / 2 1 / 2 2 1 2 (1 ) ( 1) M n x M n nx e n M e − = + − + − = − 1 0 0 ] ( 1) exp[ 1 1 1 ( 1) M n n s c n N n n n M P 由于 2 1 3 1 1 ( , , , ) P P R R R R R R c M = K Rm统计独立同分布,联合概率等于M-1个边缘概率的乘积 s N0 — 符号SNR
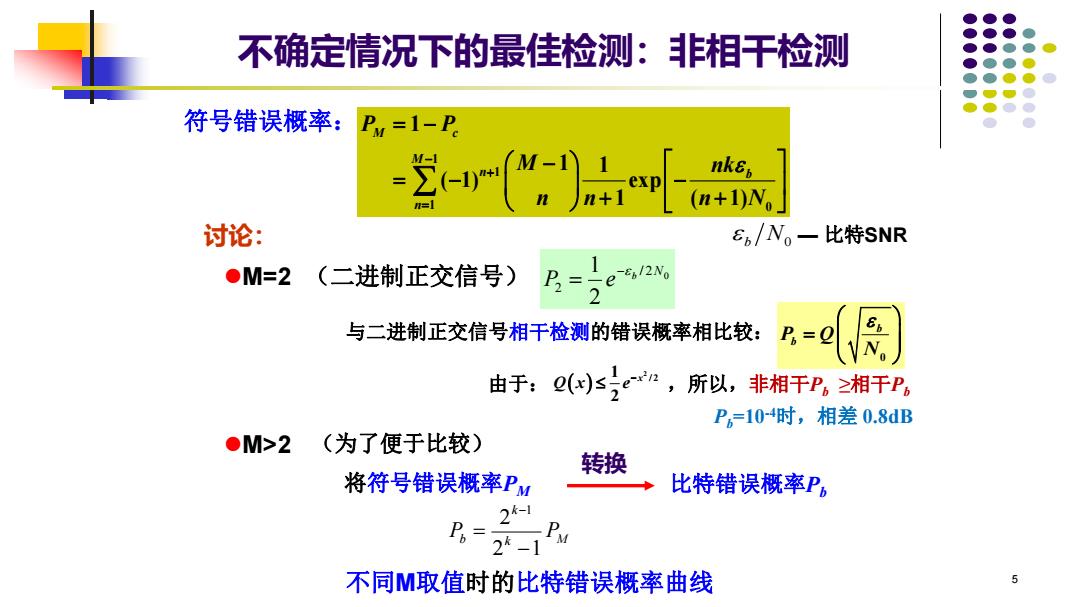
不确定情况下的最佳检测:非相干检测 符号错误概率:P=1-P (n+1)N 讨论: Eb/N。一比特SNR ●M=2 (二进制正交信号) =e12w 2 与二进制正交信号相干检测的错误概率相比较: P,= N 由于:Q()sen,所以,非相干P。≥相干P。 P。=104时,相差0.8dB ●M>2 (为了便于比较) 转换 将符号错误概率PM 比特错误概率P。 2- 27 不同M取值时的比特错误概率曲线 5
5 不确定情况下的最佳检测:非相干检测 2 0 / 2 2 1 b N P e − = 1 1 1 0 1 1 1 ( 1) exp 1 ( 1) M c M n b n P P M nk n n n N − + = = − − = − − + + 符号错误概率: 讨论: ⚫M=2 (二进制正交信号) k M k Pb P 2 1 2 1 − = − ⚫M>2 将符号错误概率PM 比特错误概率Pb 转换 不同M取值时的比特错误概率曲线 (为了便于比较) b N0 — 比特SNR 与二进制正交信号相干检测的错误概率相比较: 0 b P Q b N = ( ) 2 1 / 2 2 x Q x e− 由于: ,所以,非相干Pb ≥相干Pb Pb=10-4时,相差 0.8dB
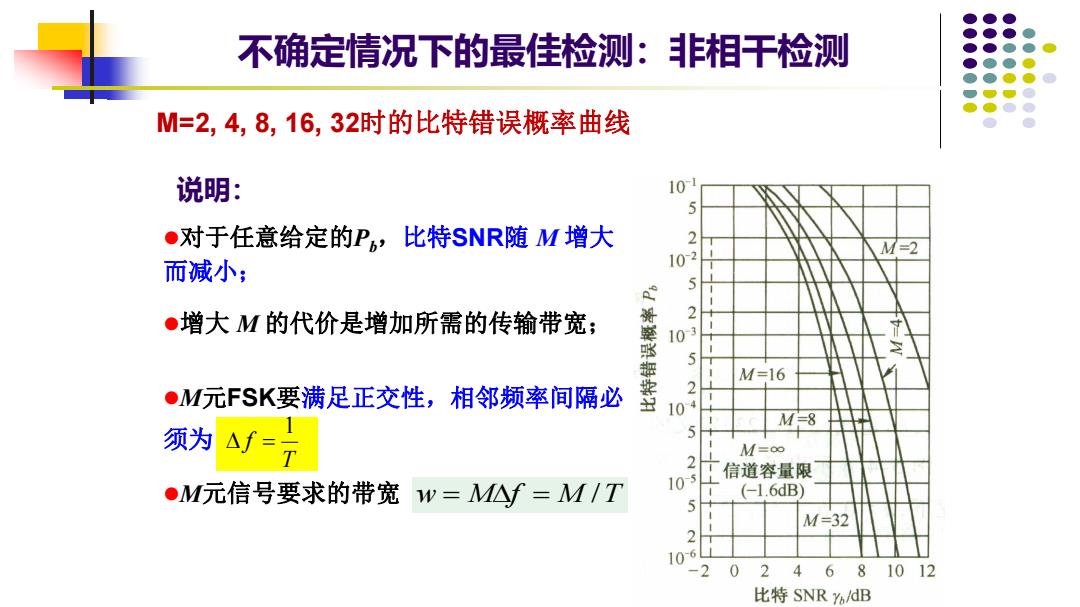
不确定情况下的最佳检测:非相干检测 M=2,4,8,16,32时的比特错误概率曲线 说明: 10- 5 ●对于任意给定的Pb,比特SNR随M增大 2 M=2 而减小; 102 5 ●增大M的代价是增加所需的传输带宽; 2 103 5 M=16 2 ●M元FSK要满足正交性,相邻频率间隔必 104 须为f=月 M=8 5 M=o∞ 2 信道容量限 ●M元信号要求的带宽w=M△f=M/T 105L (-1.6dB) 5 M=32 2 106LL -20 2 4 6 81012 比特SNRY%/dB
⚫对于任意给定的Pb,比特SNR随 M 增大 而减小; ⚫增大 M 的代价是增加所需的传输带宽; 6 不确定情况下的最佳检测:非相干检测 w = Mf = M /T 说明: M=2, 4, 8, 16, 32时的比特错误概率曲线 T f 1 = ⚫M元FSK要满足正交性,相邻频率间隔必 须为 ⚫M元信号要求的带宽

4.5.4相关二进制信号包络检测 的错误概率 7
7 4.5.4 相关二进制信号包络检测 的错误概率

不确定情况下的最佳检测:非相干检测 二进制等能量相关信号包络检测的性能 (p*0) 两个信号相关时,解调器输出: (复随机变量) h=2εcos0+nc+j2εsinp+n,) r2 =28p cos(o-do)+ne+j(28psin(o-a)+ns) 检测器:依据包络R1=、R2=r2进行判决(这两个包络是相关的) 假定发送信号是s),如同前面推导,R1、R2的边缘PDF均服从 Rice分布: R>0 P(R)=28No 0 R<0 其中m=1,2,B,=2s,B2=2Ep 8
8 不确定情况下的最佳检测:非相干检测 2 cos( ) (2 sin( ) ) 2 cos (2 sin ) 2 0 2 0 2 1 1 1 c s c s r n j n r n j n = − + + − + = + + + 2 2 0 0 0 0 exp( ) ( ) 0 ( ) 2 4 2 0 0 m m m m m m m m R R R I R P R N N N R + − = 其中 m =1,2, 1 = 2, 2 = 2 二进制等能量相关信号包络检测的性能 两个信号相关时,解调器输出: (复随机变量) 检测器:依据包络 R1=|r1 |、R2=|r2 | 进行判决(这两个包络是相关的) 假定发送信号是s1 (t),如同前面推导,R1、R2的边缘PDF均服从 Rice分布: ( ≠ 0)

不确定情况下的最佳检测:非相干检测 因p0,信号非正交,R1与R2统计相关,错误概率:(通过计算二重积分得到) B=PR>R)=P心,: R1,R2的联合PDF 方法二: 错误概率: P=P(R>R)=P(R2>R2)=P(R2-R2>0) 包络检波 平方律检波 经推导: (略) P=,(a,b)-e-a+b21(ab) 其中:a= 1-V1-lp) 9
9 不确定情况下的最佳检测:非相干检测 1 2 1 1 2 1 2 0 ( ) ( , ) b x P P R R P x x dx dx = = 错误概率: ( ) ( ) ( 0) 2 1 2 2 2 1 2 Pb = P R2 R1 = P R2 R = P R − R 方法二: ( ) 2 1 ( , ) 0 ( )/ 2 1 2 2 P Q a b e I ab a b b − + = − R1 , R2 的联合PDF 包络检波 平方律检波 其中: 2 0 (1 1 ) 2 b b N (1 1 ) = + + 2 2 0 = − − N a b 经推导: (略) 因 ≠0,信号非正交,R1与R2统计相关,错误概率:(通过计算二重积分得到)
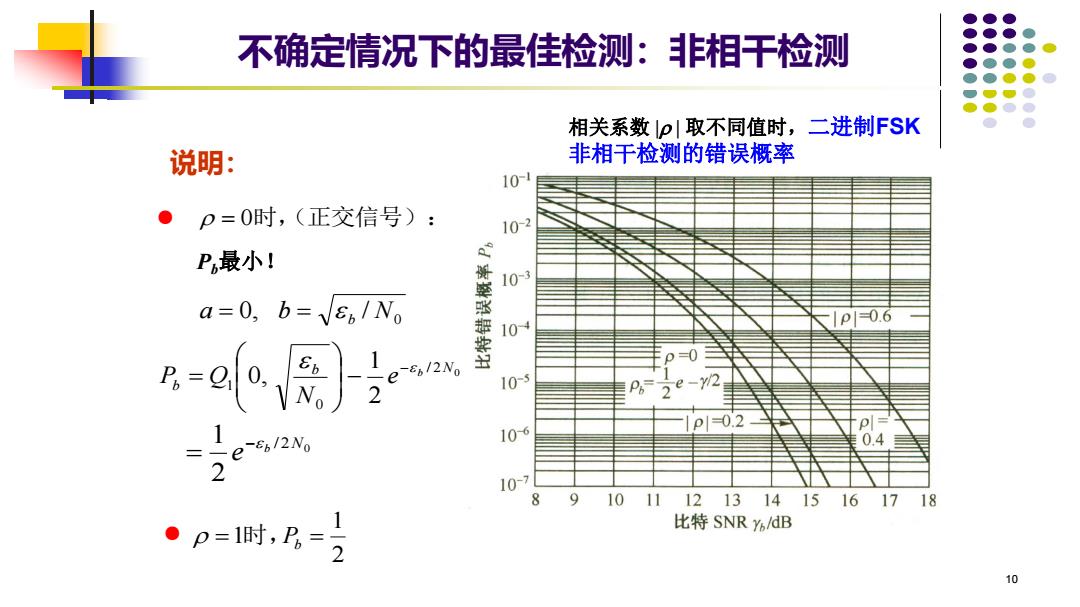
不确定情况下的最佳检测:非相干检测 相关系数p取不同值时,二进制FSK 说明: 非相干检测的错误概率 10 p=0时,(正交信号): ● 10-2 P最小I 10- a=0,b=s/No 104 、1p=0.6 a-alo 0=0 10-3 Po=2e-y2 p|=0.2 2e2 109 0.4 10-7 8 9.1011 12131415161718 0p=1时,P,= 比特SNR Yh/dB 2 10
10 0 a = 0, b = b / N 2 0 / 0 1 2 1 0, b N b b e N P Q − − = = 0时,(正交信号): 2 0 / 2 1 b N e − = 2 1 =1时,Pb = 说明: ● ● 相关系数 | | 取不同值时,二进制FSK 非相干检测的错误概率 不确定情况下的最佳检测:非相干检测 Pb最小!