
第2章交流电路的基本分析方法 学习本章应深入理解正弦量的相量表示 三种基本元件的相量模型;理解阻抗、导纳的 概念;初步理解利用阻抗、导纳来分析简单交 流电路的方法;结合仿真理解无功功率、有功 功率、谐振、功率因素等交流电路基础概念
第2章 交流电路的基本分析方法 学习本章应深入理解正弦量的相量表示、 三种基本元件的相量模型;理解阻抗、导纳的 概念;初步理解利用阻抗、导纳来分析简单交 流电路的方法;结合仿真理解无功功率、有功 功率、谐振、功率因素等交流电路基础概念

第二章第1部分 在本次课中,将介绍正弦量的概念、正 弦量的描述及其相量表示
第二章第1部分 在本次课中,将介绍正弦量的概念、正 弦量的描述及其相量表示

相关知识点与学习目标 本课涉及正弦量的3要素、正弦量的相量表示 方法2个知识点,通过本课学习,应深入理解正 弦量的3要素,掌握正弦量的相量表示方法
相关知识点与学习目标 本课涉及正弦量的3要素、正弦量的相量表示 方法2个知识点,通过本课学习,应深入理解正 弦量的3要素,掌握正弦量的相量表示方法
正弦交流电的引入 上一章我们介绍的 其中的电压、电流的 是直流电路。 大小和方向是不随时 间而变化的 在生产和日常生活中经常涉及的交流电 (如照明电)一般都是正弦交流电。 正弦交流电路是电工电子技术中的一个 重要部分
一.正弦交流电的引入 在生产和日常生活中经常涉及的交流电 (如照明电)一般都是正弦交流电。 上一章我们介绍的 是直流电路。 其中的电压、电流的 大小和方向是不随时 间而变化的 正弦交流电路是电工电子技术中的一个 重要部分
二。 什么是正弦量 随时间按正弦规律变化的电压或电流,称为正 为正弦量 2元 ωt i()=I sin(at+e) r=20ln50t+60口) 对任一正弦量,当其幅值工m(20)、角频率) (5)和初相位日(60°)确定以后,该正弦量就 能完全确定下来。因此,, 幅值、角频率和初相位称 为正弦量的三要素
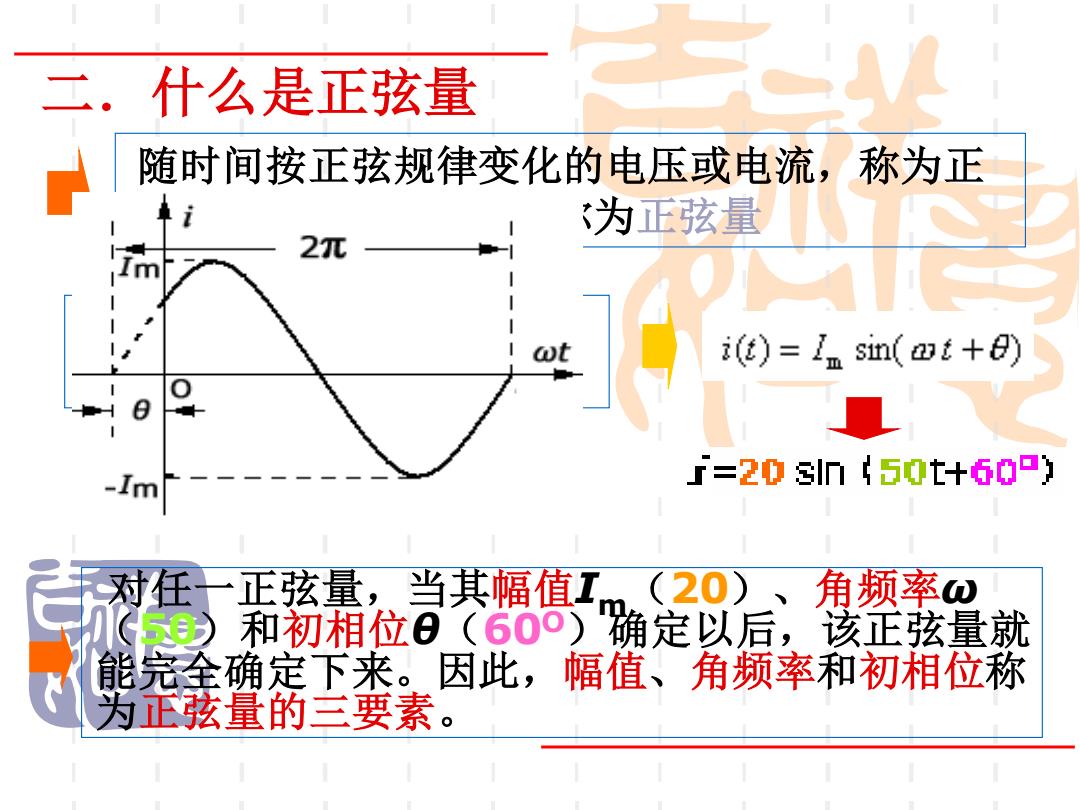
二.什么是正弦量 对任一正弦量,当其幅值Im(20)、角频率ω (50)和初相位θ(60O)确定以后,该正弦量就 能完全确定下来。因此,幅值、角频率和初相位称 为正弦量的三要素。 以电流为例,正弦量的时 间函数定义为 随时间按正弦规律变化的电压或电流,称为正 弦电压或正弦电流,统称为正弦量
三.正弦量的幅值、有效值 i(t)=I sin(at+0) r=20m50t+60) 正弦量在整个振荡过程中达到的最大值称为幅值。它 是瞬时值中的最大值。幅值用下标m表示,如Im表示 电流的幅值。 十幅值、瞬时值都不能 工程中通常采用有 效值表示周期量的 确切反映它们在电路转 换能量方面的效应。 大小
三.正弦量的幅值、有效值 正弦量在整个振荡过程中达到的最大值称为幅值。它 是瞬时值中的最大值。幅值用下标m表示,如Im表示 电流的幅值。 幅值、瞬时值都不能 确切反映它们在电路转 换能量方面的效应。 工程中通常采用有 效值表示周期量的 大小

i(t)=sin(t+θ) r=20ln50t+60口) 将一个周期量在一个周期内作用于电阻产生的热量 换算为热效应与之相等的直流量,以衡量和比较周 期量的效应,这一直流量的大小就称为周期量的有 效值,用相对应的大写字母表示。 周期电流的有效值为 PRdt=P'RT d 式是周期量的有效值的通用公式,有效值又 称为均方根值
将一个周期量在一个周期内作用于电阻产生的热量 换算为热效应与之相等的直流量,以衡量和比较周 期量的效应,这一直流量的大小就称为周期量的有 效值,用相对应的大写字母表示。 周期电流的有效值为 上式是周期量的有效值的通用公式,有效值又 称为均方根值

周期电流的有效值为 i(t)=I sin(t+θ) 计算正 弦电流的 有效值 1-cos2(w1+e) Jo 2 可见,正弦量的有效值等于其幅值乘以0.707。 =20ln50t+60) 有效值等于14.14 天 不加说明, 正弦电压、电流的大小一般皆指其有效值 可通过一个例题理解
周期电流的有效值为 可见,正弦量的有效值等于其幅值乘以0.707。 计算正 弦电流的 有效值 有效值等于14.14 不加说明,正弦电压、电流的大小一般皆指其有效值 可通过一个例题理解

【例附3.1】己知u=Umsinwt.,Um=310V,f=50Hz,试求有效值U和t=1/10s的瞬时值 解: (1) 有效值为 U 310 涵 U=1 =220V 22 秋私 雨 (2)t=1/10s的瞬时值 u (t)=Umsin2 nt ft=310sin 100x-0 10

四.正弦量的角频率、频率与周期 正弦量的角频率ω、频率f 2元 =2死 和周期T三者的关系为 我国电力工业标准频率是50Hz,它的周期为20mS 主角频率为314rad/S 可通过史个例题理解
四.正弦量的角频率、频率与周期 我国电力工业标准频率是50Hz,它的周期为20mS, 角频率为314rad/S 正弦量的角频率ω、频率f 和周期T三者的关系为 可通过一个例题理解