
高等数学川课程教学大纲 (Advanced Mathematics II) 一、课程基本信息 课程编号:10062303-4 课程类别:学科基础课 适用专业:农科类本科各专业 学分:7 总学时:112其中理论学时:112,实验学时:0 先修课程:无 后续课程:无 课程简介: 本课程系统介绍一元函数的极限、连续、导数、微分及其应用、不定积分、定积分及其应用 微分方程及其应用:行列式、矩阵的基本运算、向量组线性相关性的理论、线性方程组的解的理论 和求解方法:概率论的基本概念、事件概率的多种求法、随机变量及其分布的理论、随机变量的数 字特征的求值方法。 主要教学方法与手段: 以讲授为主,辅之以多媒体教学、习题课和课外辅导,注重理论联系实际。 选用教材: 刘金林.高等数学(经济管理类)(第4版)[M].北京:机械工业出版社,2013: 陈建华.线性代数(第4版)[].北京:机械工业出版社,2016: 宗序平概率论与数理统计(第3版)[].北京:机械工业出版社,2011: 必读书目:无 选读书目: [1]杨棋喻主编.高等数学Ⅱ[.北京:高等教育出版社,2010: [2]王玉民杜晓林主编.高等数学[M.北京:中国农业出版社,2013: [3]张良云主编.线性代数(第3版)[M.北京:高等教有出版社,2010: [4)同济大学数学系编.线性代数(第5版)[W.北京:高等教育出版社,2007 [5]张国权刘金山主编.应用概率统计[.北京:中国农业出版社,2015: [6]盛骤谢式千潘承毅主编.概率论与数理统计(第5版)[M0.北京:高等教有出版 社,2010: [7][美]Morris K1ine著.古今数学思想(英文版,1-3)[M.上海:上海科技出版社,2014: [8]A history of mathematics an introduction Victor J.Katz Addison-Wesley, 19982nded: 二、课程总目标 本课程是高等学校农科类本科各专业必修的重要基础课。通过本课程的学习,使学生对高等数 学、线性代数、概率论的基本概念、基本理论、基本方法有比较系统的认识,构建较为宽广的知识 结构。逐步培养学生抽象概括问题的能力、一定的逻辑推理能力、比较熟练的运算能力和自学能力, 提高学生在数学方面的素质和修养,培养学生综合运用所学知识分析问题、解决问题的能力,学会 运用本课程提供的数学思想、数学方法解决简单的应用问题,激发学生的探索与创新意识,为学习 其它基础课程和专业课程打下基础。 三、课程教学内容与教学要求
1 高等数学 II 课程教学大纲 (Advanced Mathematics II) 一、课程基本信息 课程编号:10062303-4 课程类别:学科基础课 适用专业:农科类本科各专业 学 分:7 总 学 时:112 其中理论学时:112, 实验学时:0 先修课程:无 后续课程:无 课程简介: 本课程系统介绍一元函数的极限、连续、导数、微分及其应用、不定积分、定积分及其应用、 微分方程及其应用;行列式、矩阵的基本运算、向量组线性相关性的理论、线性方程组的解的理论 和求解方法;概率论的基本概念、事件概率的多种求法、随机变量及其分布的理论、随机变量的数 字特征的求值方法。 主要教学方法与手段: 以讲授为主,辅之以多媒体教学、习题课和课外辅导,注重理论联系实际。 选用教材: 刘金林.高等数学(经济管理类)(第 4 版)[M].北京:机械工业出版社,2013; 陈建华.线性代数(第 4 版)[M].北京:机械工业出版社,2016; 宗序平.概率论与数理统计(第 3 版)[M].北京:机械工业出版社,2011; 必读书目:无 选读书目: [1] 杨棋喻主编.高等数学Ⅱ[M].北京:高等教育出版社,2010; [2] 王玉民 杜晓林主编.高等数学[M].北京:中国农业出版社,2013; [3] 张良云主编.线性代数(第 3 版)[M].北京:高等教育出版社,2010; [4] 同济大学数学系编.线性代数(第 5 版)[M].北京:高等教育出版社,2007; [5] 张国权 刘金山主编.应用概率统计[M].北京:中国农业出版社,2015; [6] 盛骤 谢式千 潘承毅主编.概率论与数理统计(第 5 版)[M].北京:高等教育出版 社,2010; [7] [美] Morris Kline 著.古今数学思想(英文版,1-3)[M].上海:上海科技出版社,2014; [8] A history of mathematics : an introduction Victor J. Katz Addison-Wesley, 1998 2nd ed ; 二、课程总目标 本课程是高等学校农科类本科各专业必修的重要基础课。通过本课程的学习,使学生对高等数 学、线性代数、概率论的基本概念、基本理论、基本方法有比较系统的认识,构建较为宽广的知识 结构。逐步培养学生抽象概括问题的能力、一定的逻辑推理能力、比较熟练的运算能力和自学能力, 提高学生在数学方面的素质和修养,培养学生综合运用所学知识分析问题、解决问题的能力,学会 运用本课程提供的数学思想、数学方法解决简单的应用问题,激发学生的探索与创新意识,为学习 其它基础课程和专业课程打下基础。 三、课程教学内容与教学要求
1、教学内容与学时分配 课程总学时:112学时,其中讲授学时:112学时:实验(上机)学时:0学时 教学内容与学时分配建议如下 教学章节名称 学时分配 序 教学章节名称 学时分配 号 讲课 实验 号 讲课实验 向量组的线性相关性 预备知识 4 8 与矩阵的秩 6 极限与连续 12 9 线性方程组 4 3 一元函数微分学 20 10机事件与率 8 4 一元函数积分学 20 11 随机变量及其分布 12 微分方程及其应用 12 随机变量的数字特征 4 6 行列式 6 7 矩阵及其运算 8 合计 112 2、教学要 本课程是高等学校农科类本科各专业的一门必修的重要基础课。在课程教学中,以启发式课堂讲 授为主,结合各种教学方法 有意识地增加训练、启发思维、培养能力,通过借助现代化教学工 和教学手段,逐步培养和提高学生的抽象、推理、归纳能力,研究问题、解决问题的能力,自我获 取知识的能力,使学生在今后的学习和工作中能通过自学、分析、研究得以提高。 本课程具体章节的教学目标、教学内容、教学重点、教学难点如下: 第一章预备知识(4学时) 教学目标:理解函数的概念 ,复合函数、分段函数的概念 解函数的有界性、单调性 周期性和奇偶性.掌握函数的表示法、基本初等函数的性质及其图形。 教学内容 第一节函数概念 一、区间和邻域 二、函数概念 第二节函数的几种特性 有界性 二、单调性 三、奇偶性 四、周期性 第二节反函新 第四节 基本初等函数及其图形 第五节 初等函数 第六节极坐标 本章重点:函数的几种特性,复合函数、初等函数。 本章难点:复合函数。 第二章极限与连续(12学时) 教学目标: 了解数列及函数极限的概念,理解左极限与右极限 无穷小量、无穷大量、函数连续性 等概念:会判别函数间断点的类型,理解闭区间上连续函数的性质:掌握极限的性质及 四则运算法则,掌握利用两个重要极限求极限的方法,掌握无穷小量的比较方法,会用 等价无穷小量求极限:了解连续函数的性质和初等函数的连续性。 教学内容: 第一节数列的极限 2
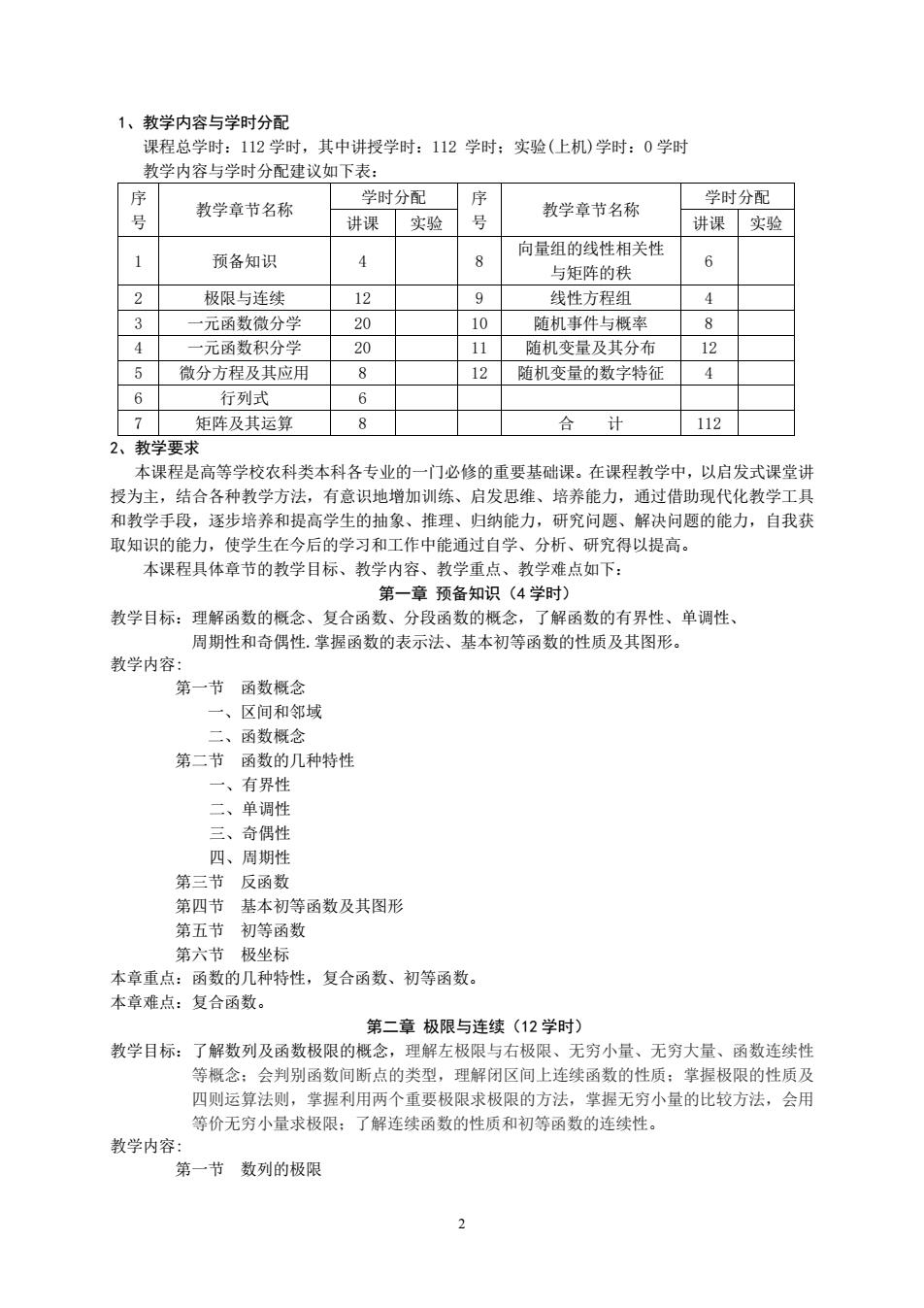
2 1、教学内容与学时分配 课程总学时:112 学时,其中讲授学时:112 学时;实验(上机)学时:0 学时 教学内容与学时分配建议如下表: 序 号 教学章节名称 学时分配 序 号 教学章节名称 学时分配 讲课 实验 讲课 实验 1 预备知识 4 8 向量组的线性相关性 与矩阵的秩 6 2 极限与连续 12 9 线性方程组 4 3 一元函数微分学 20 10 随机事件与概率 8 4 一元函数积分学 20 11 随机变量及其分布 12 5 微分方程及其应用 8 12 随机变量的数字特征 4 6 行列式 6 7 矩阵及其运算 8 合 计 112 2、教学要求 本课程是高等学校农科类本科各专业的一门必修的重要基础课。在课程教学中,以启发式课堂讲 授为主,结合各种教学方法,有意识地增加训练、启发思维、培养能力,通过借助现代化教学工具 和教学手段,逐步培养和提高学生的抽象、推理、归纳能力,研究问题、解决问题的能力,自我获 取知识的能力,使学生在今后的学习和工作中能通过自学、分析、研究得以提高。 本课程具体章节的教学目标、教学内容、教学重点、教学难点如下: 第一章 预备知识(4 学时) 教学目标:理解函数的概念、复合函数、分段函数的概念,了解函数的有界性、单调性、 周期性和奇偶性.掌握函数的表示法、基本初等函数的性质及其图形。 教学内容: 第一节 函数概念 一、区间和邻域 二、函数概念 第二节 函数的几种特性 一、有界性 二、单调性 三、奇偶性 四、周期性 第三节 反函数 第四节 基本初等函数及其图形 第五节 初等函数 第六节 极坐标 本章重点:函数的几种特性,复合函数、初等函数。 本章难点:复合函数。 第二章 极限与连续(12 学时) 教学目标:了解数列及函数极限的概念,理解左极限与右极限、无穷小量、无穷大量、函数连续性 等概念;会判别函数间断点的类型,理解闭区间上连续函数的性质;掌握极限的性质及 四则运算法则,掌握利用两个重要极限求极限的方法,掌握无穷小量的比较方法,会用 等价无穷小量求极限;了解连续函数的性质和初等函数的连续性。 教学内容: 第一节 数列的极限

一、数列极限的定义 二、收敛数列的性历 第二节函数的极限 x 0时函数的极限 二、x→Xo时函数的极限 第三节极限的运算法侧及存在准则 、极跟的四则运算 两个重要极限 第四节 无穷小量与无穷大量 一、无穷小量 一、于穷大量 三、无穷小量与无穷大量的关系 第五节函数的连续性 ,连续概念 二、间断点的分类 三、闭区间上连续函数的性质 本章重点:极限的概念及运算性质,两个重要极限,函数连续的概念。 木意难点:极限的橱令,两个币要极限,闭区间上连续函数的性质及其应用 第三音 元函数微分学(20学时) 教学目标:理解导数和微分的概 、导数的几何意义、函数的可导性与连续性之间的关系,了解高 阶导数的概念,:掌握导数的四则运算法则和复合函数的求导法则,掌握基木初等函数的 导数公式。会求分段函数的导数、隐函数和由参数方程所确定的函数的导数:会求简单 承数的高阶导数及平面曲线的切线方程和法线方程:了解微分的四叫运算法则和一阶微 分形式的不变性,会求函数的微分:理解并会用罗尔定理、拉格朗日中值定理,掌握用 洛必达法则:理解函数的极值概念,掌握用导数判断函数的单调性和求函数极值的方法 函数的最大值和最小值的求法及其应用.会用导数判断函数图形的凹凸性以及求函数图 形的拐点以及水平、铅直渐近线。 教学内容: 第一节导数概念 一、导数定义及几何意义 、可导性与连续性关系 第二节求导法则 一、函数和、差、积、商的求导法则 二、反函数的导数 三、复合函数求导公式 四、基本求导法则与公式 第三节高阶导数 一、高阶导数定义 一、高阶导数的计算方法 第四节隐函数与参数方程确定的函数的导数 、隐函数求导法则 、参数方程确定的函数的导数 第五节微分
3 一、数列极限的定义 二、收敛数列的性质 第二节 函数的极限 一、 x → 时函数的极限 二、 0 x → x 时函数的极限 第三节 极限的运算法则及存在准则 一、极限的四则运算 二、两个重要极限 第四节 无穷小量与无穷大量 一、无穷小量 二、无穷大量 三、无穷小量与无穷大量的关系 第五节 函数的连续性 一、连续概念 二、间断点的分类 三、闭区间上连续函数的性质 本章重点:极限的概念及运算性质,两个重要极限,函数连续的概念。 本章难点:极限的概念,两个重要极限,闭区间上连续函数的性质及其应用。 第三章 一元函数微分学(20 学时) 教学目标:理解导数和微分的概念、导数的几何意义、函数的可导性与连续性之间的关系,了解高 阶导数的概念,;掌握导数的四则运算法则和复合函数的求导法则,掌握基本初等函数的 导数公式. 会求分段函数的导数、隐函数和由参数方程所确定的函数的导数;会求简单 函数的高阶导数及平面曲线的切线方程和法线方程;了解微分的四则运算法则和一阶微 分形式的不变性,会求函数的微分;理解并会用罗尔定理、拉格朗日中值定理,掌握用 洛必达法则;理解函数的极值概念,掌握用导数判断函数的单调性和求函数极值的方法, 函数的最大值和最小值的求法及其应用.会用导数判断函数图形的凹凸性以及求函数图 形的拐点以及水平、铅直渐近线。 教学内容: 第一节 导数概念 一、导数定义及几何意义 二、可导性与连续性关系 第二节 求导法则 一、函数和、差、积、商的求导法则 二、反函数的导数 三、复合函数求导公式 四、基本求导法则与公式 第三节 高阶导数 一、高阶导数定义 二、高阶导数的计算方法 第四节 隐函数与参数方程确定的函数的导数 一、隐函数求导法则 二、参数方程确定的函数的导数 第五节 微分

一、微分定义 二、微分基本公式与运算法则 第六节微分中值定理 罗尔定理 二、拉格朗日中值定理 三、柯西中值定理 第七节罗必达法则 第八节函数的单调性判别法 一、单调性判别法 、利 单调性证明不等式 第九节函数的极值与最大(小)值 一、函数的极值和求法 二、函数的最大(小)值 第十节曲线的凸性、拐点与渐近线 函数的作图 本章重点:导数概念,求导法则,微分的概念及运算法则,中值定理及其应用,洛必达法则,函数 的单调性与曲线的四凸性,函数的极值与最值。 本章难点:导数与微分概念,复合函数、隐函数求导法则,中值定理及其应用。 第四章一元函数积分学(20学时) 教学目标:理解原函数、不定积分和定积分的概念,掌握不定积分的基本公式、不定积分和定积分 的性质及定积分中值定理 :掌握换元积分法与分部积分法,会求有理函数、 理式和简单无理函数的积分:理解积分上限的函数,会求它的导数:掌握牛倾菜布尼茨 公式:了解反常积分的概念,会计算反常积分:掌握用定积分表达和计算一些几何量。 教学内容: 第一节原函数与不定积分的杨今 一、不定积分的概念与性质 不定积分的基本公式 第二节 换元积 一、第一类换元法 、第二类换元法 第三节分部积分法 第四 简单有理函数的积分法 、有理真分式的 、部分分式的积分 第五节定积分概念与性质 一、曲边梯形的面积 定积分的定义和性质 第六节微积分基本定理 第七节定积分的: 一、定积分的换元积分法 、定积分的分步积分法 第八节定积分的应用 ·、定积分的微元法 、定积分 几何上的应用 第九节反常积分
4 一、微分定义 二、微分基本公式与运算法则 第六节 微分中值定理 一、罗尔定理 二、拉格朗日中值定理 三、柯西中值定理 第七节 罗必达法则 第八节 函数的单调性判别法 一、单调性判别法 二、利用单调性证明不等式 第九节 函数的极值与最大(小)值 一、函数的极值和求法 二、函数的最大(小)值 第十节 曲线的凸性、拐点与渐近线 第十一节 函数的作图 本章重点:导数概念,求导法则,微分的概念及运算法则,中值定理及其应用,洛必达法则,函数 的单调性与曲线的凹凸性,函数的极值与最值。 本章难点:导数与微分概念,复合函数、隐函数求导法则,中值定理及其应用。 第四章 一元函数积分学(20 学时) 教学目标:理解原函数、不定积分和定积分的概念,掌握不定积分的基本公式、不定积分和定积分 的性质及定积分中值定理;掌握换元积分法与分部积分法,会求有理函数、三角函数有 理式和简单无理函数的积分;理解积分上限的函数,会求它的导数;掌握牛顿-莱布尼茨 公式;了解反常积分的概念,会计算反常积分;掌握用定积分表达和计算一些几何量。 教学内容: 第一节 原函数与不定积分的概念 一、不定积分的概念与性质 二、不定积分的基本公式 第二节 换元积分法 一、第一类换元法 二、第二类换元法 第三节 分部积分法 第四节 简单有理函数的积分法 一、有理真分式的分解 二、部分分式的积分 第五节 定积分概念与性质 一、曲边梯形的面积 二、定积分的定义和性质 第六节 微积分基本定理 第七节 定积分的计算 一、定积分的换元积分法 二、定积分的分步积分法 第八节 定积分的应用 一、定积分的微元法 二、定积分在几何上的应用 第九节 反常积分

一、无穷限的反常积分 二、无界函数的反常积分 本章重点:不定积分的概念、性质与积分方法,定积分的概念与性质,微积分学基本公式,定积分 的微元法, 定积分在几何中的应用 本章难点:基本积分法,变上限定积分的性质及应用,定积分的微元法。 第五竟微分方程初步(8学时) 教学目标:了解微分方程及其阶、解、通解、初始条件和特解等概念:掌握变量可分离 的微分方程及一阶线性微分方程的解法,会解齐次微分方程:会用降阶法解可降阶的高 阶微分方程:理解二阶线性微分方程解的性质及解的结构定理握二阶常系数线性微 分方程的解法:会用微分方程解决一些简单的应用问题, 教学内容: 第一节微分方程的基木概今 第二节 一阶微分方程 可分离变量的微分方程 三、齐次微分方 一阶线性微分方程 第三节高阶微分方程 一、可降阶的高阶微分方程 二、线性微分方程解的结构 阶常系数齐次线性微分方程 二阶常系数非齐次线性微分方程 第四节微分方程的应用 本章重点:可分离变量的微分方程,一阶线性微分方程,二阶常系数线性微分方程。 本竞难点:一阶线性微分方程 一阶常系数非齐次线性微分方程。 六章行列式(6学时) 教学目标: 了解行列式的概念 掌握行列式的性质及用行列式的性质和行列式按行(列, 展开定理计算行列式。 教学内容: 第一节行列式的定义 二阶行列式 二、排列 三、n阶行列式的定义 第二节行列式的性质 第三节行列式的展开定理 一、金子式和代数余子式 、行列式按行(列)展开定理 第四节n阶行列式的计算 三角行列式 二、对称行列式、反对称行列式 三、行列式按行(列)展开 、范德蒙行列式 第五 克莱姆法 一、克莱姆法则 二、当=即时,线性齐次方程组有非零解的条件
5 一、无穷限的反常积分 二、无界函数的反常积分 本章重点:不定积分的概念、性质与积分方法,定积分的概念与性质,微积分学基本公式,定积分 的微元法,定积分在几何中的应用。 本章难点:基本积分法,变上限定积分的性质及应用,定积分的微元法。 第五章 微分方程初步(8 学时) 教学目标:了解微分方程及其阶、解、通解、初始条件和特解等概念;掌握变量可分离 的微分方程及一阶线性微分方程的解法,会解齐次微分方程;会用降阶法解可降阶的高 阶微分方程;理解二阶线性微分方程解的性质及解的结构定理.掌握二阶常系数线性微 分方程的解法;会用微分方程解决一些简单的应用问题. 教学内容: 第一节 微分方程的基本概念 第二节 一阶微分方程 一、可分离变量的微分方程 二、齐次微分方程 三、一阶线性微分方程 第三节 高阶微分方程 一、可降阶的高阶微分方程 二、线性微分方程解的结构 三、二阶常系数齐次线性微分方程 四、二阶常系数非齐次线性微分方程 第四节 微分方程的应用 本章重点:可分离变量的微分方程,一阶线性微分方程,二阶常系数线性微分方程。 本章难点:一阶线性微分方程,二阶常系数非齐次线性微分方程。 第六章 行列式(6 学时) 教学目标:了解行列式的概念,掌握行列式的性质及用行列式的性质和行列式按行(列) 展开定理计算行列式。 教学内容: 第一节 行列式的定义 一、二、三阶行列式 二、排列 三、n 阶行列式的定义 第二节 行列式的性质 第三节 行列式的展开定理 一、余子式和代数余子式 二、行列式按行(列)展开定理 第四节 n 阶行列式的计算 一、三角行列式 二、对称行列式、反对称行列式 三、行列式按行(列)展开 四、范德蒙行列式 第五节 克莱姆法则 一、克莱姆法则 二、当 m=n 时,线性齐次方程组有非零解的条件

本章重点:行列式的性质,行列式按行(列)展开,克莱姆法则。 本章难点:行列式的性质,行列式按行(列)展开。 第七音矩阵(8学时) 教学目标:理解矩阵、逆矩阵、矩阵的秩的概念 了解矩阵初等变换、初等矩阵的性质 矩阵等价的概念 了解分块矩阵及其运算:掌握矩阵的运算、逆矩阵的性质、矩阵可逆 的充分必要条件,掌握用初等变换求矩阵的秩和逆矩阵的方法。 教学内容: 第一节矩阵概念 第二节矩阵的运算 一、矩阵的加法 数与矩阵相乘,矩阵与矩阵相乘 二、矩阵的转置、方阵的行列式、方阵的幂、共轭矩阵 三、几种特殊类型的矩阵 第三节逆阵 、逆阵的定义、求法 可逆方阵的充要条件 第四节 矩阵的分块 本章重点:矩阵的运算,逆阵,矩阵分块法。 本章难点:矩阵的运算,逆阵。 第八竟向量组的线性相关性与矩阵的秩(6学时) 教学目标:理解维向量、向量的线性组合与线性表示、向量组线性相关、线性无关的概念:掌握 向量组线性相关 线性无关的有关性质及判别法 了解向量组的极大线性无关组和向量 组的秩的概念,会求向量组的极大线性无关组及秩。 教学内容: 第一节n维向量 一、n维向量 n维向量的运算 第二节 线性相关与线性无关 ·、线性组合、线性相关、线性无关的概 二、线性相关、线性无关的有关定理 三、向量组的笑价 第三节线性相关性的判别定理 第四节 矩阵的秩与向量组的 一、矩阵的秩、向量组的# 二、最大线性无关向量组 三、有关秩的相关定理 第五节矩阵的初等变换与初等矩阵 ,矩阵的初等变换 二、初等矩阵 三、初等矩阵与初等变换的关系 本章重点:维向量,线性相关与线性无关,矩阵的秩与向量组的秩,矩阵的初等变换。 本章难点:线性相关与线性无关,矩阵的秩与向量组的秩,矩阵的初等变换 九 章 求法,会用制等行变换解隆的 方得 的基解 6
6 本章重点:行列式的性质,行列式按行(列)展开,克莱姆法则。 本章难点:行列式的性质,行列式按行(列)展开。 第七章 矩阵(8 学时) 教学目标:理解矩阵、逆矩阵、矩阵的秩的概念;了解矩阵初等变换、初等矩阵的性质、 矩阵等价的概念,了解分块矩阵及其运算;掌握矩阵的运算、逆矩阵的性质、矩阵可逆 的充分必要条件,掌握用初等变换求矩阵的秩和逆矩阵的方法。 教学内容: 第一节 矩阵概念 第二节 矩阵的运算 一、矩阵的加法,数与矩阵相乘,矩阵与矩阵相乘 二、矩阵的转置、方阵的行列式、方阵的幂、共轭矩阵 三、几种特殊类型的矩阵 第三节 逆阵 一、逆阵的定义、求法 二、可逆方阵的充要条件 第四节 矩阵的分块 本章重点:矩阵的运算,逆阵,矩阵分块法。 本章难点:矩阵的运算,逆阵。 第八章 向量组的线性相关性与矩阵的秩(6 学时) 教学目标:理解 n 维向量、向量的线性组合与线性表示、向量组线性相关、线性无关的概念;掌握 向量组线性相关、线性无关的有关性质及判别法;了解向量组的极大线性无关组和向量 组的秩的概念,会求向量组的极大线性无关组及秩。 教学内容: 第一节 n 维向量 一、n 维向量 二、n 维向量的运算 第二节 线性相关与线性无关 一、线性组合、线性相关、线性无关的概念 二、线性相关、线性无关的有关定理 三、向量组的等价 第三节 线性相关性的判别定理 第四节 矩阵的秩与向量组的秩 一、矩阵的秩、向量组的秩 二、最大线性无关向量组 三、有关秩的相关定理 第五节 矩阵的初等变换与初等矩阵 一、矩阵的初等变换 二、初等矩阵 三、初等矩阵与初等变换的关系 本章重点:n 维向量,线性相关与线性无关,矩阵的秩与向量组的秩,矩阵的初等变换。 本章难点:线性相关与线性无关,矩阵的秩与向量组的秩,矩阵的初等变换。 第九章 线性方程组(4 学时) 教学目标:理解齐次线性方程组有非零解的充分必要条件及非齐次线性方程组有解的充分必要条件, 理解齐次线性方程组的基础解系及通解的概念;掌握齐次线性方程组的基础解系和通解的 求法,会用初等行变换求解非线性方程组

教学内容 第一节齐次线性方程组 一、方程组的解向量及性质,基础解系 二、求解齐次线性方程组 第二节非齐次线性方程组 方程组的相容、不相容:增广矩阵 解向量的性质、 求解非齐次线性方程组 本章重点:方程组的解向量,基础解系,方程组的求解方法。 本章难点:基础解系,方程组的求解方法。 第十章随机事件与概率(8学时) 教学目标:理解随机事件和样本空间的概念:熟练掌握事件之间的关系与基本运算。理解事件频率 的概念:了解随机现象的统计规律性。理解古典概率的概念:掌握概率的基本性质:理 解条件概率的概念:掌握乘法定理、全概率公式和贝叶斯公式:理解事件独立性的概念: 会应用事件的独立性进行概率计算」 教学内容 第一节随机事件 一、随机试验与随机事件 二、事件之间的关系与及运算 第二节事件的概率 ,概率的统计定义 二、古典概型 第三节概率的一般定义与性质 “、概率的一般定义 二橱率的性质 第四节条件概率与事件的独立性 一、系件概率 二、乘法公式 一、事件的独立性 四、独立试哈序列模型 第五节全概率公式与贝叶斯(Bayes)公式 ,全概率公式 、Baves公式 本章重点:随机事件,概率,条件概率与独立性,全概率公式与贝叶斯(Bayes)公式。 本章难点:条件概率与独立性,全概率公式与贝叶斯(ayes)公式。 第 一音随机弯量乃其分在(12学日时) 教学目标: 了解随机恋量的 理解分布函 掌握 弯量的描述方法 理解分布律 布密度的概念和性 布、泊松分布、 均 匀分布、指数分布和正态分布:会利用概率分布计算有关事件的概率。 教学内容 第一节随机变量的概念 第二节离散型随机变量及其概率分布 ,离散型随机变量及其概率分布 二、几种常见的离散分和 第三节随机变量的分布函数 一、分布函数的定义 二、分布函数的性质
7 教学内容: 第一节 齐次线性方程组 一、方程组的解向量及性质,基础解系 二、求解齐次线性方程组 第二节 非齐次线性方程组 一、方程组的相容、不相容;增广矩阵 二、解向量的性质、求解非齐次线性方程组 本章重点:方程组的解向量,基础解系,方程组的求解方法。 本章难点:基础解系,方程组的求解方法。 第十章 随机事件与概率(8 学时) 教学目标:理解随机事件和样本空间的概念;熟练掌握事件之间的关系与基本运算。理解事件频率 的概念;了解随机现象的统计规律性。理解古典概率的概念;掌握概率的基本性质;理 解条件概率的概念;掌握乘法定理、全概率公式和贝叶斯公式;理解事件独立性的概念; 会应用事件的独立性进行概率计算。 教学内容: 第一节 随机事件 一、随机试验与随机事件 二、事件之间的关系与及运算 第二节 事件的概率 一、概率的统计定义 二、古典概型 第三节 概率的一般定义与性质 一、概率的一般定义 二、概率的性质 第四节 条件概率与事件的独立性 一、条件概率 二、乘法公式 三、事件的独立性 四、独立试验序列模型 第五节 全概率公式与贝叶斯(Bayes)公式 一、全概率公式 二、Bayes 公式 本章重点:随机事件,概率,条件概率与独立性,全概率公式与贝叶斯(Bayes)公式 。 本章难点:条件概率与独立性,全概率公式与贝叶斯(Bayes)公式。 第十一章 随机变量及其分布(12 学时) 教学目标:了解随机变量的概念;理解分布函数的概念和性质;掌握离散型随机变量和连续型随机 变量的描述方法;理解分布律与分布密度的概念和性质。掌握二项分布、泊松分布、均 匀分布、指数分布和正态分布;会利用概率分布计算有关事件的概率。 教学内容: 第一节 随机变量的概念 第二节 离散型随机变量及其概率分布 一、离散型随机变量及其概率分布 二、几种常见的离散分布 第三节 随机变量的分布函数 一、分布函数的定义 二、分布函数的性质

第四节连续型随机变量及其分布 一、连续型随机变量及其概率密度 一、几种常见的车续型随机变量的分布 第五节随机变量的函数的分布 、离散型情开 二、连续型情形 本章重点:随机变量及其分布,随机变量函数的分布,几种重要的离散型、连续型分布。 本章难点:随机变量的函数的分布。 第十二章随机变量的数字特征(4学时) 教学目标:理解数学期望、方差的概念 ,掌握它们的性质与计算:会计算随机变量函数的数学期望 熟记二项分布、泊松分布、均匀分布、指数分布和正态分布的数学期望与方差。 教学内容 第一节数学期望 一、数学期望的定义 二、随机变量承数的数学期翅 第二节方差 方差的定义 、方差的性质 本章重点:数学期望、方差的概念,常见分布的期望和方差。 本章难点:二项分布、泊松分布、正态分布的期望和方差。 四、课程老核 考核方式:本课程考试均采取闭卷考试形式(包括期中考试与期末考试) 成绩评定:本课程采用百分制评定学习,记分方法如下:平时成绩(包括期中考试、上课 出勤、平时作业等)占30%,期末考试成绩占70%。 执笔人:孟国明 审定人:季新华 二零一五年二月 普通化学课程教学大纲 (General Chemistry) 一、课程基本信息 课程编号:10082053- 课程类别:学科基础课 适用专 农字专业 发展专业 业专业、动物医学专业、动物实验专业、动物检验专业 打物利 物科学专业、物技术专业、生物工君 专 总学时:80其中理论学时:80,实验学时:0 先修课程:无
8 第四节 连续型随机变量及其分布 一、连续型随机变量及其概率密度 二、几种常见的连续型随机变量的分布 第五节 随机变量的函数的分布 一、离散型情形 二、连续型情形 本章重点:随机变量及其分布,随机变量函数的分布,几种重要的离散型、连续型分布。 本章难点:随机变量的函数的分布。 第十二章 随机变量的数字特征(4 学时) 教学目标:理解数学期望、方差的概念,掌握它们的性质与计算;会计算随机变量函数的数学期望; 熟记二项分布、泊松分布、均匀分布、指数分布和正态分布的数学期望与方差。 教学内容: 第一节 数学期望 一、数学期望的定义 二、随机变量函数的数学期望 第二节 方差 一、方差的定义 二、方差的性质 本章重点:数学期望、方差的概念,常见分布的期望和方差。 本章难点:二项分布、泊松分布、正态分布的期望和方差。 四、课程考核 考核方式:本课程考试均采取闭卷考试形式(包括期中考试与期末考试)。 成绩评定:本课程采用百分制评定学习,记分方法如下 :平时成绩(包括期中考试、上课 出勤、平时作业等)占 30%,期末考试成绩占 70%。 执笔人:孟国明 审定人:季新华 二零一五年二月 普通化学课程教学大纲 (General Chemistry) 一、课程基本信息 课程编号:10082053-4 课程类别:学科基础课 适用专业:农学专业、农学(农业信息技术)专业、农业资源与环境专业、种子科学与工程专业、 农村区域发展专业、植物保护专业、园艺专业、园林专业、生态专业、 动物科学专业、水产专业、 草业专业、动物医学专业、动物实验专业、动物检验专业、生物科学专业、物技术专业、生物工程 专业 学 分:5 总 学 时:80 其中理论学时:80, 实验学时:0 先修课程:无
后续课程:有机化学 课程简介: 普通化学是高等农业院校教学计划中的一门基础课,是农科一年级学生的必修课。本课程以培 养高素质农业人才的目标为依据,对农科学生必须掌握的有关无机化学、分析化学、有机化学、生 物化学的基础理论、基本知识、基本技能进行了精选和整合,突出了化学与农业、植物、动物等学 科的有机联系,强化化学在农业上的应用。主婴讲授溶液、 胶体、 化学热力学、化学动力学、化学 平衡等有 化 反应的基本概 基本规律和原子 子结构基础知识 介绍滴定分析理论及名 种滴定分析方法和部分仪器分析方法。随着当前化学学科领域发展,要求在普通化学教学中既要耳 视基础理论的阐述,又要适当介绍现代化学中的新的发展,以使学生通过该课程的学习,不但掌挥 普通化学的基本内容,又适当了解现代化学的前沿研究领域,在教学中积极采用研究型教学法,充 分地发挥学生学习能动性,提高学生学习普通化学的兴趣。培养和训练学生科学的思维方法,引导 他们运用辩证唯物主义的认识论和方法论分析和解决普通化学问题。培养学生独立地进行化学计算、 自主学习和检阅参考资料等方面的能力。 主要教学方法与手段: 课堂多媒体课件结合黑板板书 选用教材: 董元意.无机及分析化学(第三版)[0.北京:科学出版社、2011 必读书目: 揭念芹.基础化学:无机及分析化学(第二版)[.北京:科学出版社、2010 选读书 华形文.普通化学原理(第四版).北京:北京大学出版社、2013 普通化等 二、 本课程教学目标是使学生通过课程学习,熟悉普通化学基本原理,掌握基本的化学知识,为今 后在专业课的学习研究中具备必要的化学基础,能够在实践或工作过程中具备必要的化学知识及技 能,并能够在分子层面作进一步深入的研究奠定基础。 三、课程教学内容与教学要求 1、教学内容与学时分配 课程总学时:80 学时 学时 序号 教学章节名称 序号 教学章节名称 验 1绪言 7第六章酸碱平衡和酸碱滴定 12 2第一章溶液和胶体 5 8第七章沉淀溶解平衡和沉淀滴定6 3第二章化学热力学基础 6 9第八章配位平衡和配位滴定 10 4第三章化学反应速率和化学平衡 8 10 第九章氧化还原平衡和氧化还原 滴定 10 5第四章原子结构、分子结构 12 11第十章吸光光度法 6 6第五章化学分析 4 12 合计 80 2、教学要求 绪论(1学时) 教学目标:了解本课程概况、学科分类、学习特点 9
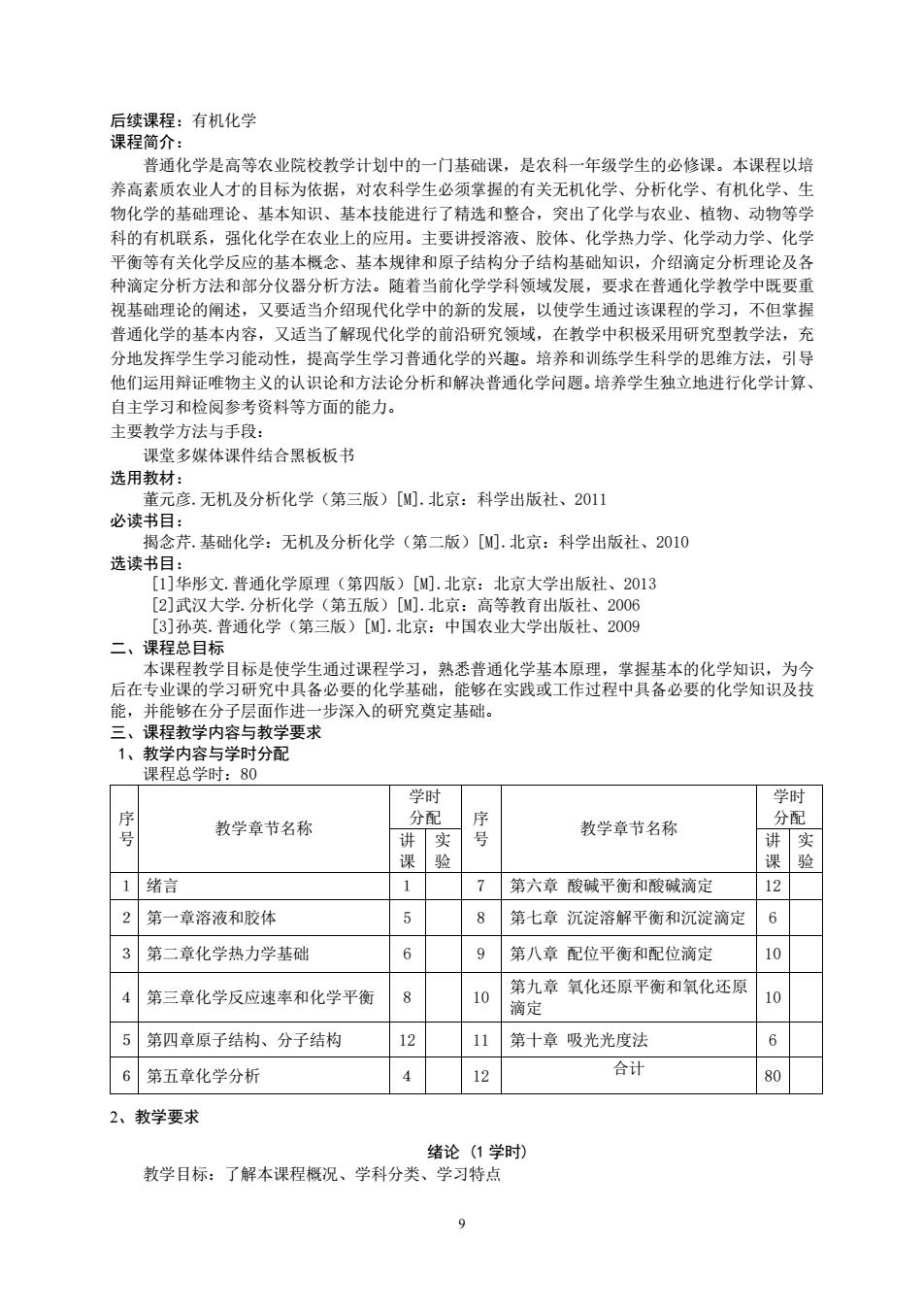
9 后续课程:有机化学 课程简介: 普通化学是高等农业院校教学计划中的一门基础课,是农科一年级学生的必修课。本课程以培 养高素质农业人才的目标为依据,对农科学生必须掌握的有关无机化学、分析化学、有机化学、生 物化学的基础理论、基本知识、基本技能进行了精选和整合,突出了化学与农业、植物、动物等学 科的有机联系,强化化学在农业上的应用。主要讲授溶液、胶体、化学热力学、化学动力学、化学 平衡等有关化学反应的基本概念、基本规律和原子结构分子结构基础知识,介绍滴定分析理论及各 种滴定分析方法和部分仪器分析方法。随着当前化学学科领域发展,要求在普通化学教学中既要重 视基础理论的阐述,又要适当介绍现代化学中的新的发展,以使学生通过该课程的学习,不但掌握 普通化学的基本内容,又适当了解现代化学的前沿研究领域,在教学中积极采用研究型教学法,充 分地发挥学生学习能动性,提高学生学习普通化学的兴趣。培养和训练学生科学的思维方法,引导 他们运用辩证唯物主义的认识论和方法论分析和解决普通化学问题。培养学生独立地进行化学计算、 自主学习和检阅参考资料等方面的能力。 主要教学方法与手段: 课堂多媒体课件结合黑板板书 选用教材: 董元彦.无机及分析化学(第三版)[M].北京:科学出版社、2011 必读书目: 揭念芹.基础化学:无机及分析化学(第二版)[M].北京:科学出版社、2010 选读书目: [1]华彤文.普通化学原理(第四版)[M].北京:北京大学出版社、2013 [2]武汉大学.分析化学(第五版)[M].北京:高等教育出版社、2006 [3]孙英.普通化学(第三版)[M].北京:中国农业大学出版社、2009 二、课程总目标 本课程教学目标是使学生通过课程学习,熟悉普通化学基本原理,掌握基本的化学知识,为今 后在专业课的学习研究中具备必要的化学基础,能够在实践或工作过程中具备必要的化学知识及技 能,并能够在分子层面作进一步深入的研究奠定基础。 三、课程教学内容与教学要求 1、教学内容与学时分配 课程总学时:80 序 号 教学章节名称 学时 分配 序 号 教学章节名称 学时 分配 讲 课 实 验 讲 课 实 验 1 绪言 1 7 第六章 酸碱平衡和酸碱滴定 12 2 第一章溶液和胶体 5 8 第七章 沉淀溶解平衡和沉淀滴定 6 3 第二章化学热力学基础 6 9 第八章 配位平衡和配位滴定 10 4 第三章化学反应速率和化学平衡 8 10 第九章 氧化还原平衡和氧化还原 滴定 10 5 第四章原子结构、分子结构 12 11 第十章 吸光光度法 6 6 第五章化学分析 4 12 合计 80 2、教学要求 绪论 (1 学时) 教学目标:了解本课程概况、学科分类、学习特点

教学内容 农业科学的关 学课程的内容 第一章分散体系5学时 教学目标:了解分散体系定义,稀溶液依数性及胶体 教学内容: 第一节溶液 一、溶液浓度的表示法 二、非电解质稀溶液的依数性 第二节胶体 一、分散体系 三、溶胶的制备和净化 第三节表面活性物质和乳状液 本章重点:稀溶液的依数性及溶胶的性质 点:溶胶的胶团结构 第二章化学热力学基础(6学时) 教学目标:初步掌握化学热力学原理、基本概念及计算 教学内容: 第一节热力学第一定律 二、基本概念 二、热力学第一定律 第二节化学反应的热效应 一、格和变 三、化学反应的格变 第三节熵变 第四节吉布斯自由能变 、吉布斯自由角 布斯自由能 能变与反 本喜直布晰服名种状态函数等基本服念:热练应用盖斯定律及热力学数指,进行常温 应的方向 下反应的标准焓变、熵变和自由能变等的计算:掌握利用自由能变化判断化学反应 方向的原理,并正确应用吉布斯一赫姆霍兹公式分析温度、格变、嫡变对化学反应自 发性的影响 难点:格变、熵变概念的理解 第三章化学反应速率和化学平衡(8学时)
10 教学内容: 一、化学与农业科学的关系 二、化学的分类及普通化学课程的内容 三、有关学习普通化学课的几个问题 第一章 分散体系(5 学时) 教学目标:了解分散体系定义,稀溶液依数性及胶体 教学内容: 第一节 溶液 一、溶液浓度的表示法 二、非电解质稀溶液的依数性 第二节 胶体 一、分散体系 二、溶胶的制备和净化 三、溶胶的性质 四、胶团结构 五、溶胶的稳定性和聚沉 六、高分子溶液 第三节 表面活性物质和乳状液 一、表面活性物质 二、乳状液 本章重点:稀溶液的依数性及溶胶的性质 难 点: 溶胶的胶团结构 第二章 化学热力学基础(6 学时) 教学目标:初步掌握化学热力学原理、基本概念及计算 教学内容: 第一节 热力学第一定律 一、基本概念 二、热力学第一定律 第二节 化学反应的热效应 一、焓和焓变 二、盖斯定律 三、化学反应的焓变 第三节 熵变 一、混乱度 二、熵和熵变 第四节 吉布斯自由能变 一、吉布斯自由能 二、标准生成吉布斯自由能 三、吉布斯自由能变与反应的方向 本章重点:掌握和区分各种状态函数等基本概念;熟练应用盖斯定律及热力学数据,进行常温 下反应的标准焓变、熵变和自由能变等的计算;掌握利用自由能变化判断化学反应 方向的原理,并正确应用吉布斯-赫姆霍兹公式分析温度、焓变、熵变对化学反应自 发性的影响 难 点:焓变、熵变概念的理解 第三章 化学反应速率和化学平衡(8 学时)