第7章偏心受压构件的正截面承载力计算 当轴向压力N的作用线偏离受压构件的轴线时[图7-1a)门,称为偏心受压构件。压力N 的作用点离构件截面形心的距离,称为偏心距。截面上同时承受轴心压力和弯矩的构件[图 7-1b)门,称为压弯构件。根据力的平移法则,截面承受偏心距为e,的偏心压力N相当于承 受轴心压力N和弯矩M(=N。)的共同作用,故压弯构件与偏心受压构件的基本受力特性 是一致的。 图71偏心受压构件与压弯构件 )偏心受压构件b)压弯构件 钢筋混凝土偏心受压(或压弯)构件是实际工程中应用较广泛的受力构件之一,例如, 拱桥的钢筋混凝士拱肋,桁架的上弦杆、刚架的立柱、柱式墩(台)的墩(台)柱等均属偏 心受压构件,在荷载作用下,构件截面上同时存在轴心压力和弯矩。 钢筋混凝土偏心受压构件的截面型式如图7-2所示。矩形截面为最常用的截面型式,截 面高度h大于600mm的偏心受压构件多采用工字形或箱形截面。圆形截面主要用于柱式墩 台、桩基础中 图7-2偏心受压构件截面型式 a矩形截面b)工字形截面c)箱形截面d圆形截面 在钢筋混凝土偏心受压构件的截面上,布置有纵向受力钢筋和箍筋。纵向受力钢筋在截 面中最常见的配置方式是将纵向钢筋集中放置在偏心方向的两对面[图7-3)],其数量通过 正截面承载力计算确定。对于圆形截面,则采用沿截面周边均匀配筋的方式[图7-3b)门。 箍筋的作用与轴心受压构件中普通箍筋的作用基本相同。此外,偏心受压构件中还存在若 定的剪力,可由箍筋负担。但因剪力的数值一般较小,故一般不予计算。箍筋数量及间距按 11
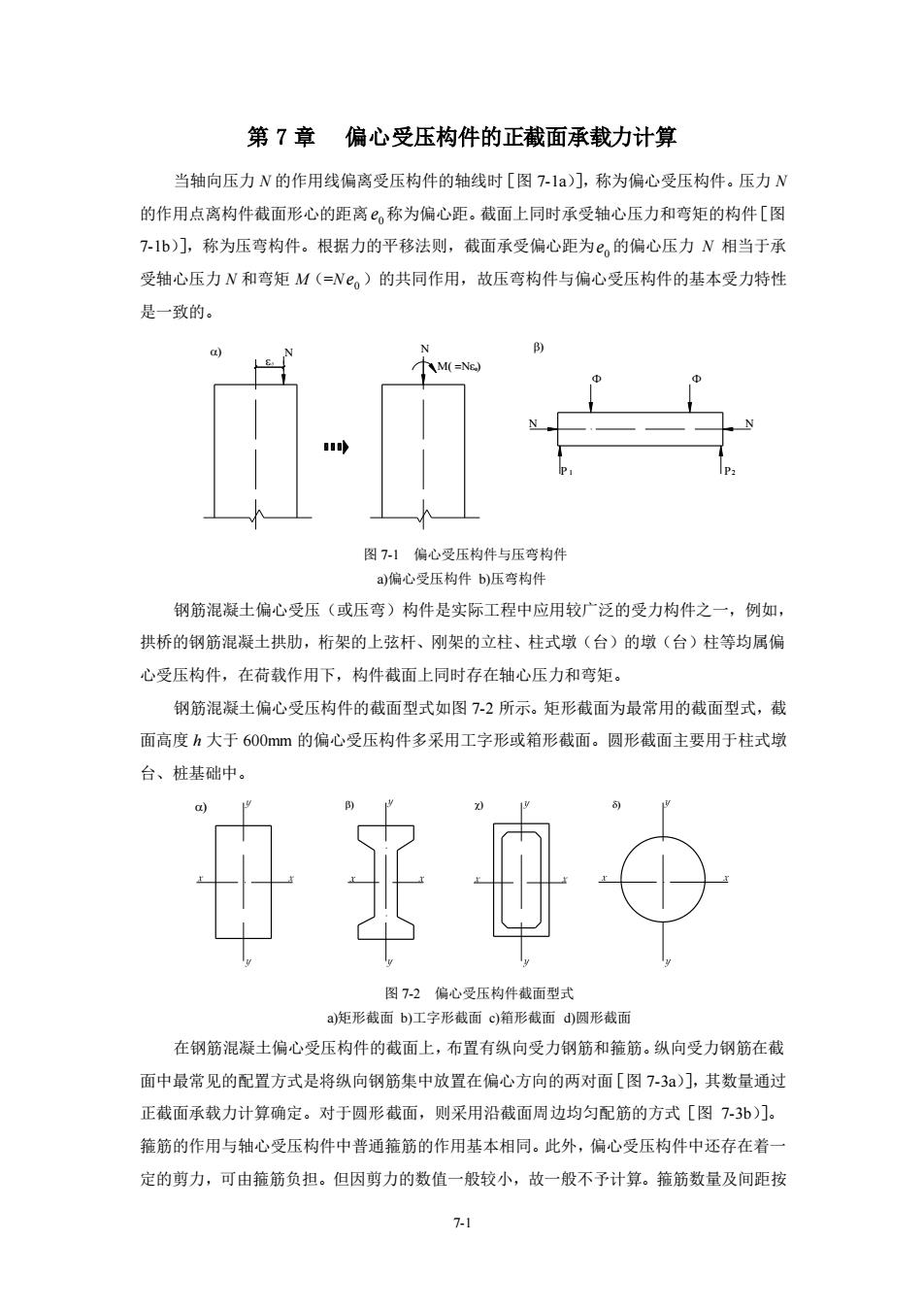
7-1 第 7 章 偏心受压构件的正截面承载力计算 当轴向压力 N 的作用线偏离受压构件的轴线时[图 7-1a)],称为偏心受压构件。压力 N 的作用点离构件截面形心的距离 0 e 称为偏心距。截面上同时承受轴心压力和弯矩的构件[图 7-1b)],称为压弯构件。根据力的平移法则,截面承受偏心距为 0 e 的偏心压力 N 相当于承 受轴心压力 N 和弯矩 M(=N 0 e )的共同作用,故压弯构件与偏心受压构件的基本受力特性 是一致的。 ) ) ( =) 图 7-1 偏心受压构件与压弯构件 a)偏心受压构件 b)压弯构件 钢筋混凝土偏心受压(或压弯)构件是实际工程中应用较广泛的受力构件之一,例如, 拱桥的钢筋混凝土拱肋,桁架的上弦杆、刚架的立柱、柱式墩(台)的墩(台)柱等均属偏 心受压构件,在荷载作用下,构件截面上同时存在轴心压力和弯矩。 钢筋混凝土偏心受压构件的截面型式如图 7-2 所示。矩形截面为最常用的截面型式,截 面高度 h 大于 600mm 的偏心受压构件多采用工字形或箱形截面。圆形截面主要用于柱式墩 台、桩基础中。 ) ) ) ) 图 7-2 偏心受压构件截面型式 a)矩形截面 b)工字形截面 c)箱形截面 d)圆形截面 在钢筋混凝土偏心受压构件的截面上,布置有纵向受力钢筋和箍筋。纵向受力钢筋在截 面中最常见的配置方式是将纵向钢筋集中放置在偏心方向的两对面[图 7-3a)],其数量通过 正截面承载力计算确定。对于圆形截面,则采用沿截面周边均匀配筋的方式[图 7-3b)]。 箍筋的作用与轴心受压构件中普通箍筋的作用基本相同。此外,偏心受压构件中还存在着一 定的剪力,可由箍筋负担。但因剪力的数值一般较小,故一般不予计算。箍筋数量及间距按

普通箍筋柱的构造要求确定。 向钢 图73偏心受压构件截面钢筋布置形式 a)飘筋集中配筋布置b)纵筋沿截面周边均匀布置 7.1偏心受压构件正截面受力特点和破坏形态 钢筋混凝土偏心受压构件也有短柱和长柱之分。本节以矩形截面的偏心受压短柱的试验 结果,介绍截面集中配筋情况下偏心受压构件的受力特点和破坏形态。 7.1.1偏心受压构件的破坏形态 钢筋混凝土偏心受压构件随着偏心距的大小及纵向钢筋配筋情况不同,有以下两种主要 破坏形态。 1)受拉破坏一大偏心受压破坏 在相对偏心距。h较大,且受拉钢筋配置得不太多时,会发生这种破坏形态。图74 为矩形截面大偏心受压短柱试件在试验荷载N作用下截面混凝土应变、应力及柱侧向变位 的发展情况。短柱受力后,截面靠近偏心压力N的一侧(钢筋为A,)受压,另一侧(钢 筋为A,)受拉。随着荷载增大,受拉区混凝土先出现横向裂缝,裂缝的开展使受拉钢筋A, 的应力增长较快,首先达到屈服。中和轴向受压边移动,受压区混凝土压应变迅速增大,最 后,受压区钢筋A屈服,混凝土达到极限压应变而压碎(图7-5)。其破坏形成与双筋矩形 截面梁的破坏形态相似, 许多大偏心受压短柱试验都表明,当偏心距较大,且受拉钢筋配筋率不高时,偏心受压 构件的破坏是受拉钢筋首先到达屈服强度然后受压混凝士土压坏。临近破坏时有明显的预兆, 裂缝显著开展,称为受拉破坏。构件的承载能力取决于受拉钢筋的强度和数量
7-2 普通箍筋柱的构造要求确定。 纵向钢筋 箍筋 纵向钢筋 箍筋 纵向钢筋 纵向钢筋 箍筋 箍筋 ) ) 图 7-3 偏心受压构件截面钢筋布置形式 a)纵筋集中配筋布置 b)纵筋沿截面周边均匀布置 7.1 偏心受压构件正截面受力特点和破坏形态 钢筋混凝土偏心受压构件也有短柱和长柱之分。本节以矩形截面的偏心受压短柱的试验 结果,介绍截面集中配筋情况下偏心受压构件的受力特点和破坏形态。 7.1.1 偏心受压构件的破坏形态 钢筋混凝土偏心受压构件随着偏心距的大小及纵向钢筋配筋情况不同,有以下两种主要 破坏形态。 1)受拉破坏——大偏心受压破坏 在相对偏心距 0 e /h 较大,且受拉钢筋配置得不太多时,会发生这种破坏形态。图 7-4 为矩形截面大偏心受压短柱试件在试验荷载 N 作用下截面混凝土应变、应力及柱侧向变位 的发展情况。短柱受力后,截面靠近偏心压力 N 的一侧(钢筋为 ' As )受压,另一侧(钢 筋为 As )受拉。随着荷载增大,受拉区混凝土先出现横向裂缝,裂缝的开展使受拉钢筋 As 的应力增长较快,首先达到屈服。中和轴向受压边移动,受压区混凝土压应变迅速增大,最 后,受压区钢筋 ' As 屈服,混凝土达到极限压应变而压碎(图 7-5)。其破坏形成与双筋矩形 截面梁的破坏形态相似。 许多大偏心受压短柱试验都表明,当偏心距较大,且受拉钢筋配筋率不高时,偏心受压 构件的破坏是受拉钢筋首先到达屈服强度然后受压混凝土压坏。临近破坏时有明显的预兆, 裂缝显著开展,称为受拉破坏。构件的承载能力取决于受拉钢筋的强度和数量
图& 为图 贺翅 柱半高度侧向李农出归) 图74大偏心受压短柱试件(尺寸单位:mm 0) B) 图75大偏心受压短柱的破坏形态(尺寸单位:mm) a破坏形态b)局部放大 2)受压破坏一小偏心受压破坏 小偏心受压就是压力N的初始偏心距,较小的情况。图7-6为矩形截面小偏心受压短 柱试件的试验结果。该试件的截面尺寸,配筋均与图74所示试件相同,但偏心距较小, e,=25mm。由图7-6可见,短柱受力后,截面全部受压,其中,靠近偏心压力N的一侧(钢 筋为A,)受到的压应力较大,另一侧(钢筋为A,)压应力较小。随着偏心压力N的逐渐增 加,混凝土应力也增大。当靠近N一侧的混凝土压应变达到其极限压应变时,压区边缘混 凝土压碎,同时,该侧的受压钢筋A也达到屈服:但是,破坏时另一侧的混凝土和钢筋A 的应力都很小,在临近破坏时,受拉一侧才出现短而小的裂缝(图7-7)。 根据以上试验以及其它短柱的试验结果,依偏心距,的大小及受拉区纵向钢筋A,数 量,小偏心受压短柱破坏时的截面应力分布,可分为图7-8所示的几种情况。 入3
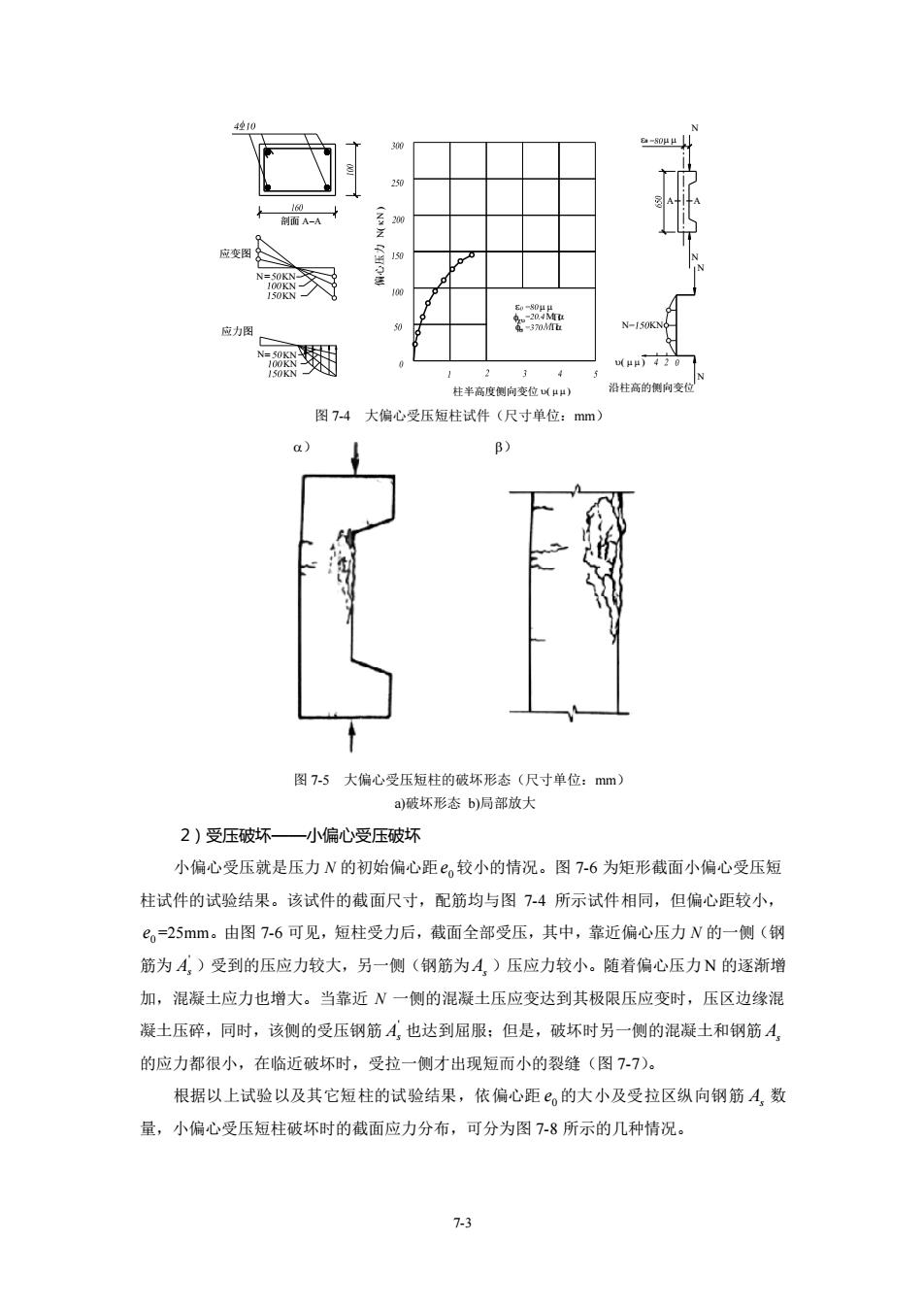
7-3 = 应力图 应变图 = 剖面 − 柱半高度侧向变位 ( ) 沿柱高的侧向变位 ( ) 偏心压力 ( ) 图 7-4 大偏心受压短柱试件(尺寸单位:mm) 图 7-5 大偏心受压短柱的破坏形态(尺寸单位:mm) a)破坏形态 b)局部放大 2)受压破坏——小偏心受压破坏 小偏心受压就是压力 N 的初始偏心距 0 e 较小的情况。图 7-6 为矩形截面小偏心受压短 柱试件的试验结果。该试件的截面尺寸,配筋均与图 7-4 所示试件相同,但偏心距较小, 0 e =25mm。由图 7-6 可见,短柱受力后,截面全部受压,其中,靠近偏心压力 N 的一侧(钢 筋为 ' As )受到的压应力较大,另一侧(钢筋为 As )压应力较小。随着偏心压力 N 的逐渐增 加,混凝土应力也增大。当靠近 N 一侧的混凝土压应变达到其极限压应变时,压区边缘混 凝土压碎,同时,该侧的受压钢筋 ' As 也达到屈服;但是,破坏时另一侧的混凝土和钢筋 As 的应力都很小,在临近破坏时,受拉一侧才出现短而小的裂缝(图 7-7)。 根据以上试验以及其它短柱的试验结果,依偏心距 0 e 的大小及受拉区纵向钢筋 As 数 量,小偏心受压短柱破坏时的截面应力分布,可分为图 7-8 所示的几种情况。 ) )
应变图 力图 N-2KN 沿柱高的侧向变 图7-6小偏心受压短柱试验 B) 图7-7小偏心受压短柱破坏形态 a被坏形态b)局部放大 (1)当纵向偏心压力偏心距很小时,构件截面将全部受压,中和轴位于截面以外[图 7-8a)门。破坏时,靠近压力N一侧混凝土应变达到极限压应变,钢筋A达到屈服强度,而 离纵向压力较远一侧的混凝士和受压钢筋均未达到其抗压强度。 (2)纵向压力偏心距很小,但是离纵向压力较远一侧钢筋A数量少而靠近纵向力N 一侧钢筋A,较多时,则藏面的实际重心轴就不在混凝土截面形心轴0-0处[图7-8c)]而向 右偏移至11轴。这样,截面靠近纵向力N的一侧,即原来压应力较小而A布置得过少的 一侧,将负担较大的压应力。于是,尽管仍是全截面受压,但远离纵向力N一侧的钢筋A, 将由于混凝土的应变达到极限压应变而屈服,但靠近纵向力N一侧的钢筋A,的应力有可能 达不到屈服强度。 (3)当纵向力偏心距较小时,或偏心距较大而受拉钢筋A,较多时,截面大部分受压而 小部分受拉[图7-8b)]。中和轴距受拉钢筋A,很近,钢筋A,中的拉应力很小,达不到屈服 强度
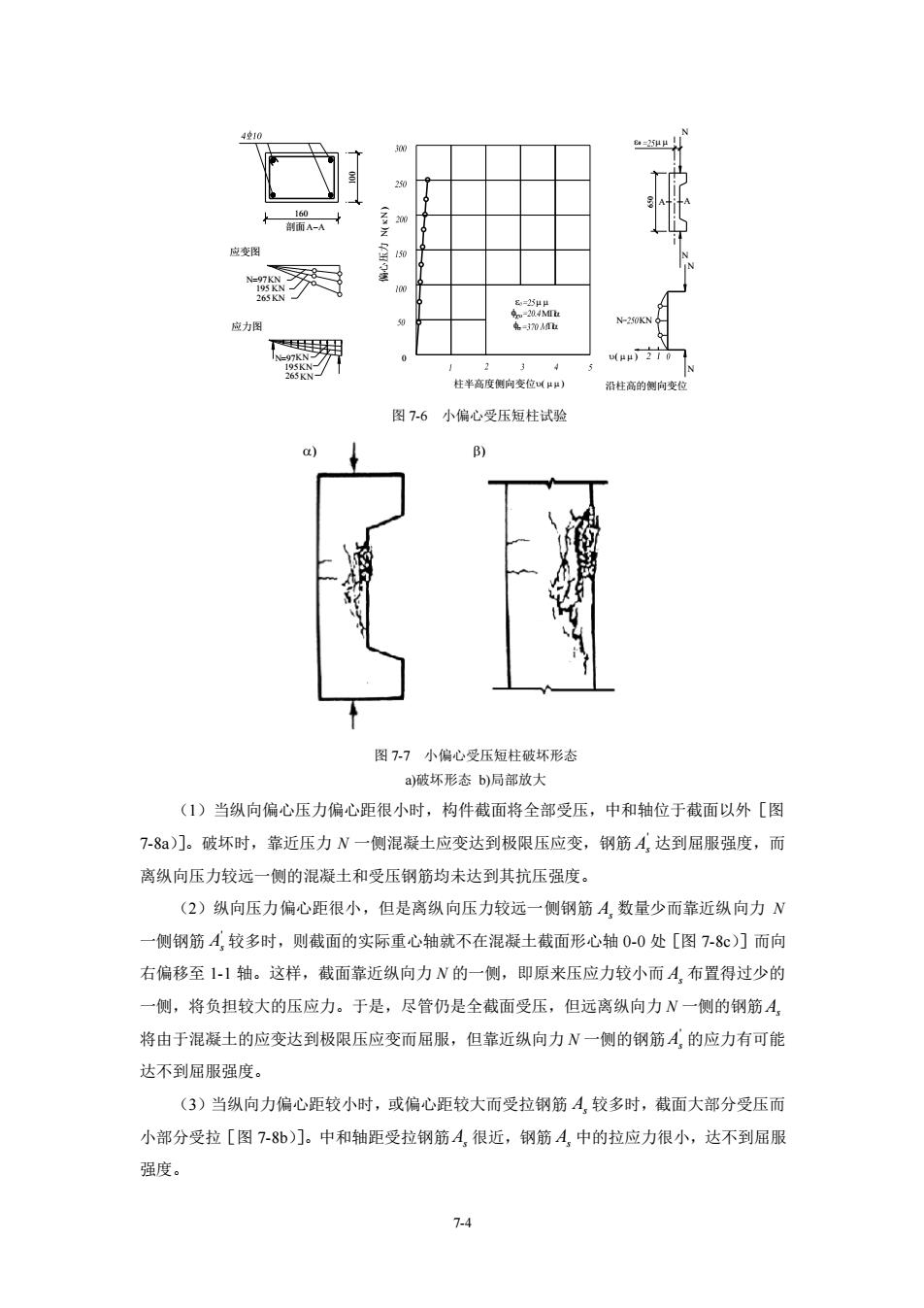
7-4 = 应力图 应变图 = 剖面 − 柱半高度侧向变位 ( ) 沿柱高的侧向变位 ( ) 偏心压力 ( ) 图 7-6 小偏心受压短柱试验 图 7-7 小偏心受压短柱破坏形态 a)破坏形态 b)局部放大 (1)当纵向偏心压力偏心距很小时,构件截面将全部受压,中和轴位于截面以外[图 7-8a)]。破坏时,靠近压力 N 一侧混凝土应变达到极限压应变,钢筋 ' As 达到屈服强度,而 离纵向压力较远一侧的混凝土和受压钢筋均未达到其抗压强度。 (2)纵向压力偏心距很小,但是离纵向压力较远一侧钢筋 As 数量少而靠近纵向力 N 一侧钢筋 ' As 较多时,则截面的实际重心轴就不在混凝土截面形心轴 0-0 处[图 7-8c)]而向 右偏移至 1-1 轴。这样,截面靠近纵向力 N 的一侧,即原来压应力较小而 As 布置得过少的 一侧,将负担较大的压应力。于是,尽管仍是全截面受压,但远离纵向力 N 一侧的钢筋 As 将由于混凝土的应变达到极限压应变而屈服,但靠近纵向力 N 一侧的钢筋 ' As 的应力有可能 达不到屈服强度。 (3)当纵向力偏心距较小时,或偏心距较大而受拉钢筋 As 较多时,截面大部分受压而 小部分受拉[图 7-8b)]。中和轴距受拉钢筋 As 很近,钢筋 As 中的拉应力很小,达不到屈服 强度。 ) )

B) 图7-8小偏心受压短柱酸面受力的几种情况 a)藏面全部受压的应力图b)截面大部受压的应力图©A,太少时的应力图 总而言之,小偏心受压构件的破坏一般是受压区边缘混凝士的应变达到极限压应变,受 压区混凝土被压碎:同一侧的钢筋压应力达到屈服强度,而另一侧的钢筋,不论受拉还是受 压,其应力均达不到屈服强度,破坏前构件横向变形无明显的急剧增长,这种破坏被称为“受 压破坏”,其正截面承载力取决于受压区混凝土抗压强度和受压钢筋强度。 7.1.2大、小偏心受压的界限 图7-9表示矩形截面偏心受压构件的混凝土应变分布图形,图中b、线表示在大偏 心受压状态下的截面应变状态。随者纵向压力的偏心距减小或受拉钢筋配筋率的增加,在破 坏时形成斜线d所示的应变分布状态,即当受拉钢筋达到屈服应变£,时,受压边缘混凝士 也刚好达到极限压应变值6,这就是界限状态。若纵向压力的偏心距进一步减小或受拉钢 筋配筋量进一步增大,则截面破坏时将形成斜线所示的受拉钢筋达不到屈服的小偏心受 压状态。 当进入全截面受压状态后,混凝土受压较大一侧的边缘极限压应变将随着纵向压力N 偏心距的减小而逐步有所下降,其截面应变分布如斜线叭ag和垂直线ah所示顺序变化, 在变化的过程中,受压边缘的极限压应变将由6逐步下降到接近轴心受压时的0.002。 上述偏心受压构件截面部分受压、部分受拉时的应变变化规律与受弯构件截面应变变化 是相似的,因此,与受弯构件正截面承载力计算相同,可用受压区界限高度x或相对界限 受压区高度5。来判别两种不同偏心受压破坏形态:当:≤5时,截面为大偏心受压破坏: 当5>5时,截面为小偏心受压破坏。乐值可由表3-2查得
7-5 ) ) ) 图 7-8 小偏心受压短柱截面受力的几种情况 a)截面全部受压的应力图 b)截面大部受压的应力图 c)As太少时的应力图 总而言之,小偏心受压构件的破坏一般是受压区边缘混凝土的应变达到极限压应变,受 压区混凝土被压碎;同一侧的钢筋压应力达到屈服强度,而另一侧的钢筋,不论受拉还是受 压,其应力均达不到屈服强度,破坏前构件横向变形无明显的急剧增长,这种破坏被称为“受 压破坏”,其正截面承载力取决于 受压区混凝土抗压强度和受压钢筋强度。 7.1.2 大、小偏心受压的界限 图 7-9 表示矩形截面偏心受压构件的混凝土应变分布图形,图中 ab、ac 线表示在大偏 心受压状态下的截面应变状态。随着纵向压力的偏心距减小或受拉钢筋配筋率的增加,在破 坏时形成斜线 ad 所示的应变分布状态,即当受拉钢筋达到屈服应变 y 时,受压边缘混凝土 也刚好达到极限压应变值 cu ,这就是界限状态。若纵向压力的偏心距进一步减小或受拉钢 筋配筋量进一步增大,则截面破坏时将形成斜线 ae 所示的受拉钢筋达不到屈服的小偏心受 压状态。 当进入全截面受压状态后,混凝土受压较大一侧的边缘极限压应变将随着纵向压力 N 偏心距的减小而逐步有所下降,其截面应变分布如斜线 af、a g ' 和垂直线 a h '' 所示顺序变化, 在变化的过程中,受压边缘的极限压应变将由 cu 逐步下降到接近轴心受压时的 0.002。 上述偏心受压构件截面部分受压、部分受拉时的应变变化规律与受弯构件截面应变变化 是相似的,因此,与受弯构件正截面承载力计算相同,可用受压区界限高度 b x 或相对界限 受压区高度 b 来判别两种不同偏心受压破坏形态:当 ≤ b 时,截面为大偏心受压破坏; 当 > b 时,截面为小偏心受压破坏。 b 值可由表 3-2 查得

儿何鞋 68◆Yn 色w 图7.9偏心受压构件的截面应变分布 7.1.3偏心受压构件的M-N相关曲线 偏心受压构件是弯矩和轴力共同作用的构件,轴力与弯矩对于构件的作用效应存在着叠 加和制约的关系,亦即当给定轴力N时,有其唯一对应的弯矩M,或者说构件可以在不同 的N和M的组合下达到其极限承载能力。 对于偏心受压短柱,由其截面承载力的计算分析可以得到图7-10所示的偏心受压构件 MN相关曲线图。在图70中,动段表示大偏心受压时的MN相关曲线,为二次抛物线。 随着轴向压力N的增大,截面能承担的弯矩也相应提高。 b点为钢筋与受压混凝土同时达到其强度极限值的界限状态。此时,偏心受压构件承受 的弯矩M最大。 图7-10偏心受压构件的N曲线图 cb段表示小偏心受压时的MN相关曲线,是一条接近于直线的二次函数曲线。由曲线 走向可以看出,在小偏心受压情况下,随者轴向压力的增大,截面所能承担的弯矩反而降低。 在图7-10中,c点表示轴心受压的情况,a点表示受弯构件的情况。图中曲线上的任 点d的坐标就代表截面强度的一种M和V的组合。若任意点d位于曲线ac的内侧,说明 截面在该点坐标给出的M和N的组合未达到承载能力极限状态:若d点位于图中曲线b 的外侧则表明截面的承载力不足
7-6 几何轴线 图 7-9 偏心受压构件的截面应变分布 7.1.3 偏心受压构件的 M-N 相关曲线 偏心受压构件是弯矩和轴力共同作用的构件,轴力与弯矩对于构件的作用效应存在着叠 加和制约的关系,亦即当给定轴力 N 时,有其唯一对应的弯矩 M,或者说构件可以在不同 的 N 和 M 的组合下达到其极限承载能力。 对于偏心受压短柱,由其截面承载力的计算分析可以得到图 7-10 所示的偏心受压构件 M-N 相关曲线图。在图 7-10 中,ab 段表示大偏心受压时的 M-N 相关曲线,为二次抛物线。 随着轴向压力 N 的增大,截面能承担的弯矩也相应提高。 b 点为钢筋与受压混凝土同时达到其强度极限值的界限状态。此时,偏心受压构件承受 的弯矩 M 最大。 ( ) 受 压 破 坏 受 拉 破 坏 图 7-10 偏心受压构件的 M-N 曲线图 cb 段表示小偏心受压时的 M-N 相关曲线,是一条接近于直线的二次函数曲线。由曲线 走向可以看出,在小偏心受压情况下,随着轴向压力的增大,截面所能承担的弯矩反而降低。 在图 7-10 中,c 点表示轴心受压的情况,a 点表示受弯构件的情况。图中曲线上的任一 点 d 的坐标就代表截面强度的一种 M 和 N 的组合。若任意点 d 位于曲线 abc 的内侧,说明 截面在该点坐标给出的 M 和 N 的组合未达到承载能力极限状态;若 d 点位于图中曲线 abc 的外侧则表明截面的承载力不足

72偏心受压构件的纵向弯曲 钢筋混凝土受压构件在承受偏心力作用后,将产生纵向弯曲变形,即会产生侧向变形(变 位)。对于长细比小的短柱,侧向挠度小,计算时一般可忽略其影响。而对长细比较大的长 柱,由于侧向变形的影响,各截面所受的弯矩不再是We,而变成N(。+y)(图7I1),y 为构件任意点的水平侧向变形。在柱高度中点处,侧向变形最大,截面上的弯矩为N(,+W)。 ▣随着荷载的增大而不断加大,因而弯矩的增长也越来越快。一般把偏心受压构件截面弯矩 中的N,称为初始弯矩或一阶弯矩(不考虑构件侧向变形时的弯矩),将Mu或My称为附 加弯矩或二阶弯矩。由于二阶弯矩的影响,将造成偏心受压构件不同的破坏类型。 N() 图-1偏心受压构件的受力图式 7.2.1偏心受压构件的破坏类型 钢筋混凝士偏心受压构件按长细比可分为短柱、长柱和细长柱。 1)短柱偏心受压短柱中,虽然偏心力作用将产生一定的侧向变形,但其值很小 一般可忽略不计。即可以不考虑二阶弯矩,各截面中的弯矩均可认为等于N。,弯矩M与 轴向力N呈线性关系。 随着荷载的增大,当短柱达到极限承载能力时,柱的截面由于材料达到其极限强度而破 坏。在MN相关图中,从加载到破坏的路径为直线,当直线与截面承载力线相交于B点时 就发生材料破坏,即图7-12中的OB直线。 2)长柱矩形截面柱,当8<h≤30时即为长柱。长柱受偏心力作用时的侧向变形u 较大,二阶弯矩影响已不可忽视,因此,实际偏心距是随荷载的增大而非线性增加,构件控 制截面最终仍然是由于截面中材料达到其强度极限而破坏,属材料破坏。图-3为偏心受 压长柱的试验结果。其截面尺寸、配筋与图7-6所示短柱相同,但其长细比为h=15.6,最 终破坏形态仍为小偏心受压,但偏心距已随N值的增加而变大。 偏心受压长柱在MN相关图上从加荷到破坏的受力路径为曲线,与截面承载力曲线相 交于C点而发生材料破坏,即图7-12中0C曲线。 7.7
7-7 7.2 偏心受压构件的纵向弯曲 钢筋混凝土受压构件在承受偏心力作用后,将产生纵向弯曲变形,即会产生侧向变形(变 位)。对于长细比小的短柱,侧向挠度小,计算时一般可忽略其影响。而对长细比较大的长 柱,由于侧向变形的影响,各截面所受的弯矩不再是 Ne0 ,而变成 0 N e y ( ) + (图 7-11),y 为构件任意点的水平侧向变形。在柱高度中点处,侧向变形最大,截面上的弯矩为 0 N e u ( ) + 。 u 随着荷载的增大而不断加大,因而弯矩的增长也越来越快。一般把偏心受压构件截面弯矩 中的 Ne0 称为初始弯矩或一阶弯矩(不考虑构件侧向变形时的弯矩),将 Nu 或 Ny 称为附 加弯矩或二阶弯矩。由于二阶弯矩的影响,将造成偏心受压构件不同的破坏类型。 =( +) 图 7-11 偏心受压构件的受力图式 7.2.1 偏心受压构件的破坏类型 钢筋混凝土偏心受压构件按长细比可分为短柱、长柱和细长柱。 1)短柱 偏心受压短柱中,虽然偏心力作用将产生一定的侧向变形,但其 u 值很小, 一般可忽略不计。即可以不考虑二阶弯矩,各截面中的弯矩均可认为等于 Ne0 ,弯矩 M 与 轴向力 N 呈线性关系。 随着荷载的增大,当短柱达到极限承载能力时,柱的截面由于材料达到其极限强度而破 坏。在 M-N 相关图中,从加载到破坏的路径为直线,当直线与截面承载力线相交于 B 点时 就发生材料破坏,即图 7-12 中的 OB 直线。 2)长柱 矩形截面柱,当 8<l0/h≤30 时即为长柱。长柱受偏心力作用时的侧向变形 u 较大,二阶弯矩影响已不可忽视,因此,实际偏心距是随荷载的增大而非线性增加,构件控 制截面最终仍然是由于截面中材料达到其强度极限而破坏,属材料破坏。图 7-13 为偏心受 压长柱的试验结果。其截面尺寸、配筋与图 7-6 所示短柱相同,但其长细比为 l0/h =15.6,最 终破坏形态仍为小偏心受压,但偏心距已随 N 值的增加而变大。 偏心受压长柱在 M-N 相关图上从加荷到破坏的受力路径为曲线,与截面承载力曲线相 交于 C 点而发生材料破坏,即图 7-12 中 OC 曲线
短柱《材料环 长柱〔材料被坏 长柱(失稳破 图7-12构件长细比的影响 3)细长柱长细比很大的柱。当偏心压力N达到最大值时(图7-12中E点),侧向变 形突然剧增,此时,偏心受压构件截面上钢筋和混凝士的应变均未达到材料破坏时的极限 值,即压杆达到最大承载能力是发生在其控制截面材料强度还未达到其破坏强度,这种破坏 类型称为失稳破坏。在构件失稳后,若控制作用在构件上的压力逐渐减小以保持构件继续变 形,则随着增大到一定值及相应的荷载下,截面也可达到材料破坏点(点E)。但这时的 承载能力已明显低于失稳时的破坏荷载。由于失稳破坏与材料破坏有本质的区别,设计中 般尽量不采用细长柱。 在图712中,短柱、长柱和细长柱的初始偏心距是相同的,但破坏类型不同:短柱利 长柱分别为OB和OC受力路径,为材料破坏:细长柱为OE受力路径,失稳破坏。随者长 细比的增大,其承载力N值也不同,其值分别为N。、N和N2,而N。>N>N N 柱半高度侧向变位】 N 图7-13偏心受压长柱的试验与破坏(尺寸单位:mm)
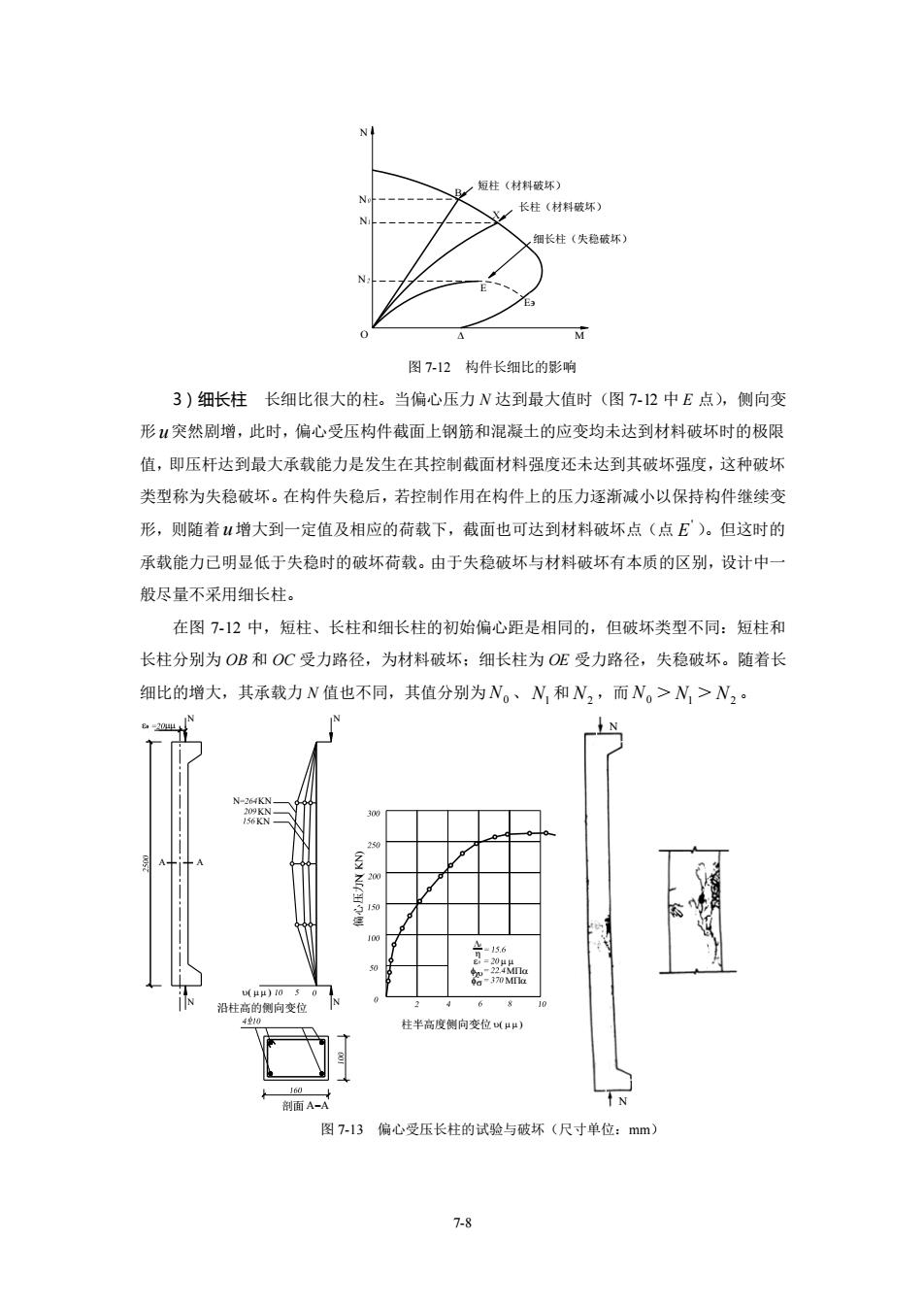
7-8 长柱(材料破坏) 细长柱(失稳破坏) 短柱(材料破坏) 图 7-12 构件长细比的影响 3)细长柱 长细比很大的柱。当偏心压力 N 达到最大值时(图 7-12 中 E 点),侧向变 形 u 突然剧增,此时,偏心受压构件截面上钢筋和混凝土的应变均未达到材料破坏时的极限 值,即压杆达到最大承载能力是发生在其控制截面材料强度还未达到其破坏强度,这种破坏 类型称为失稳破坏。在构件失稳后,若控制作用在构件上的压力逐渐减小以保持构件继续变 形,则随着 u 增大到一定值及相应的荷载下,截面也可达到材料破坏点(点 ' E )。但这时的 承载能力已明显低于失稳时的破坏荷载。由于失稳破坏与材料破坏有本质的区别,设计中一 般尽量不采用细长柱。 在图 7-12 中,短柱、长柱和细长柱的初始偏心距是相同的,但破坏类型不同:短柱和 长柱分别为 OB 和 OC 受力路径,为材料破坏;细长柱为 OE 受力路径,失稳破坏。随着长 细比的增大,其承载力 N 值也不同,其值分别为 N0 、 N1 和 N2 ,而 N0 > N1 > N2 。 偏心压力 ( ) 剖面 − 柱半高度侧向变位 ( ) 沿柱高的侧向变位 ( ) 图 7-13 偏心受压长柱的试验与破坏(尺寸单位:mm)

7.2.2偏心距增大系数 实际工程中最常遇到的是长柱,由于最终破坏是材料破坏,因此,在设计计算中需考虑 由于构件侧向变形(变位)而引起的二阶弯矩的影响。 偏心受压构件控制截面的实际弯矩应为 M=N(e+u)=N +u e 令 刀=6+”=1+“ (7-1) M=N.neo 刀称为偏心受压构件考虑纵向挠曲影响(二阶效应)的轴向力偏心距增大系数。 由式(7-1)可见,n越大表明二阶弯矩的影响越大,则藏面所承担的一阶弯矩N,在 总弯矩中所占比例就相对越小。应该指出的是,当,=0时,式(?)是无意义的。当偏心 受压构件为短柱时,则7=1。 《公路桥规》根据偏心压杆的极限曲率理论分析,规定偏心距增大系数计算表达式为 (7-2) 51=02+272≤10 (7-3a) 6=15-001≤10 (7-3b) 式中一一构件的计算长度,可参照表6-1或按工程经验确定 ,一—轴向力对截面重心轴的偏心距: 么一一截面的有效高度。对圆形截面取=r+,r及意义详见7.5节: h一截面的高度。对圆形截面取h=d,d,为圆形截面直径: 一一荷载偏心率对截面曲率的影响系数: 52—构件长细比对截面曲率的影响系数。 《公路桥规》规定,计算偏心受压构件正截面承载力时,对长细比L。>17.5(1为构 件裁面回转半径)的构件或长细比,h(矩形截面)>5、长细比,/d,(圆形截面)>4.4的构件 应考虑构件在弯矩作用平面内的变形(变位)对轴向力偏心距的影响。此时,应将轴向力对 截面重心轴的偏心距e,乘以偏心距增大系数)。 偏心受压构件的弯矩作用平面的意义见图-14的示意图。应该指出的,前述偏心受 压构件的破坏类型及破坏形态,均指在弯矩作用平面的受力情况。 7.9
7-9 7.2.2 偏心距增大系数 实际工程中最常遇到的是长柱,由于最终破坏是材料破坏,因此,在设计计算中需考虑 由于构件侧向变形(变位)而引起的二阶弯矩的影响。 偏心受压构件控制截面的实际弯矩应为 0 0 0 0 ( ) e u M N e u N e e + = + = 令 0 0 0 1 e u u e e + = = + (7-1) 则 0 M = N e 称为偏心受压构件考虑纵向挠曲影响(二阶效应)的轴向力偏心距增大系数。 由式(7-1)可见, 越大表明二阶弯矩的影响越大,则截面所承担的一阶弯矩 Ne0 在 总弯矩中所占比例就相对越小。应该指出的是,当 0 e =0 时,式(7-1)是无意义的。当偏心 受压构件为短柱时,则 = 1。 《公路桥规》根据偏心压杆的极限曲率理论分析,规定偏心距增大系数 计算表达式为 0 2 1 2 0 0 1 1 ( ) 1400( ) l e h h = + (7-2) 0 1 0 0.2 2.7 e h = + ≤1.0 (7-3a) h l 0 2 =1.15 − 0.01 ≤1.0 (7-3b) 式中 0 l ——构件的计算长度,可参照表 6-1 或按工程经验确定; 0 e ——轴向力对截面重心轴的偏心距; 0 h ——截面的有效高度。对圆形截面取 s h = r + r 0 , r 及 s r 意义详见 7.5 节; h ——截面的高度。对圆形截面取 h = d1, 1 d 为圆形截面直径; 1 ——荷载偏心率对截面曲率的影响系数; 2 ——构件长细比对截面曲率的影响系数。 《公路桥规》规定,计算偏心受压构件正截面承载力时,对长细比 o l i >17.5( i 为构 件截面回转半径)的构件或长细比 0 l h (矩形截面)>5、长细比 0 1 l d (圆形截面)>4.4 的构件, 应考虑构件在弯矩作用平面内的变形(变位)对轴向力偏心距的影响。此时,应将轴向力对 截面重心轴的偏心距 0 e 乘以偏心距增大系数 。 偏心受压构件的弯矩作用平面的意义见图 7-14 的示意图。应该指出的,前述偏心受 压构件的破坏类型及破坏形态,均指在弯矩作用平面的受力情况

矩作用平面 直于弯矩作用平面 图7-14矩形截面偏心受压构件的弯矩作用平面示意图 7.3矩形截面偏心受压构件 钢筋混凝士矩形截面偏心受压构件是工程中应用最广泛的构件,其截面长边为,短边 为b。在设计中,应该以长边方向的截面主轴面xx为弯矩作用平面(图7-14)。 矩形偏心受压构件的纵向钢筋一般集中布置在弯矩作用方向的截面两对边位置上,以 A,和A,来分别代表离偏心压力较远一侧和较近一侧的钢筋面积。当A,≠A,时,称为非对 称布筋:当A,=A,时,称为对称布筋。 7.3.1矩形截面偏心受压构件正截面承载力计算的基本公式 与受弯构件相似,偏心受压构件的正截面承载力计算采用下列基本假定: (1)截面应变分布符合平截面假定: (2)不考虑混凝土的抗拉强度: (3)受压混凝土的极限压应变6=0.0033~0.003,详见3.3.2节: (4)混凝土的压应力图形为矩形,应力集度为∫。,矩形应力图的高度x取等于按平 截面确定的受压区高度x乘以系数B,即x=。 矩形截面偏心受压构件正截面承载力计算图式如图7-15。 对于矩形截面偏心受压构件,用,表示纵向弯曲的影响,只要是材料破坏类型,无论 是大偏心受压破坏,还是小偏心受压破坏,受压区边缘混凝土都达到极限压应变,同一侧的 受压钢筋A,一般都能达到抗压强度设计值∫,而对面一侧的钢筋A,的应力,可能受拉 (达到或未达到抗拉强度设计值∫),也可能受压,故在图-15中以。,表示A,钢筋中的 应力,从而可以建立一种包括大、小偏心受压情况的统一正截面承载力计算图式。 7-10
7-10 弯矩作用平面 垂直于弯矩作用平面 图 7-14 矩形截面偏心受压构件的弯矩作用平面示意图 7.3 矩形截面偏心受压构件 钢筋混凝土矩形截面偏心受压构件是工程中应用最广泛的构件,其截面长边为 h,短边 为 b。在设计中,应该以长边方向的截面主轴面 x-x 为弯矩作用平面(图 7-14)。 矩形偏心受压构件的纵向钢筋一般集中布置在弯矩作用方向的截面两对边位置上,以 As 和 ' As 来分别代表离偏心压力较远一侧和较近一侧的钢筋面积。当 As ≠ ' As 时,称为非对 称布筋;当 As = ' As 时,称为对称布筋。 7.3.1 矩形截面偏心受压构件正截面承载力计算的基本公式 与受弯构件相似,偏心受压构件的正截面承载力计算采用下列基本假定: (1)截面应变分布符合平截面假定; (2)不考虑混凝土的抗拉强度; (3)受压混凝土的极限压应变 0.0033 ~ 0.003 cu = ,详见 3.3.2 节; (4)混凝土的压应力图形为矩形,应力集度为 cd f ,矩形应力图的高度 x 取等于按平 截面确定的受压区高度 c x 乘以系数 ,即 c x = x 。 矩形截面偏心受压构件正截面承载力计算图式如图 7-15。 对于矩形截面偏心受压构件,用 0 e 表示纵向弯曲的影响,只要是材料破坏类型,无论 是大偏心受压破坏,还是小偏心受压破坏,受压区边缘混凝土都达到极限压应变,同一侧的 受压钢筋 ' As ,一般都能达到抗压强度设计值 ' sd f ,而对面一侧的钢筋 As 的应力,可能受拉 (达到或未达到抗拉强度设计值 sd f ),也可能受压,故在图 7-15 中以 s 表示 As 钢筋中的 应力,从而可以建立一种包括大、小偏心受压情况的统一正截面承载力计算图式