
第4章受弯构件斜截面承载力计算 受弯构件在荷截作用下,各截面上除产生弯矩外,一般同时还有剪力。在受弯构件设 计中,首先应使构件的截面具有足够的抗弯承载力,即必须进行正截面抗弯承载力计算,这 在第3章中己介绍过。此外,在剪力和弯矩共同作用的区段,有可能发生沿斜截面的破坏, 故受弯构件还必须进行斜截面承载力计算。 本章主要讨论斜截面承载力的计算。 4.1受弯构件斜截面的受力特点和破坏形态 在第3章受湾构件的构造中,介绍过钢筋混凝土梁设置的箍筋和弯起(斜)钢筋都起 抗剪作用。一般把箍筋和弯起(斜)钢筋统称为梁的腹筋。把配有纵向受力钢筋和腹筋的梁 称为有腹梁筋:而把仅有纵向受力钢筋而不设腹筋的梁称为无腹筋梁。在对受弯构件斜截面 受力分析中,为了便于探讨剪切破坏的特性,常以无腹筋梁为基础,再引伸到有腹筋梁。 4.1.1无腹筋简支梁斜裂缝出现前后的受力状态 图41为一无腹筋简支梁,作用有两个对称的集中荷载。CD段称为纯弯段:AC段和 DB段内的截面上既有弯矩M又有剪力,故称为剪弯段。 当梁上荷载较小时,裂缝尚未出现,钢筋和混凝土的应力-应变关系都处在弹性阶段 所以,把梁近似看作匀质弹性体,可用材料力学方法来分析它的应力状态。 在剪弯区段截面上任一点都有剪应力和正应力存在,由单元体应力状态可知,它们的 共同作用将产生主拉应力σm和主压应力σ。,图41即为这种情况下无腹筋简支梁的主应 力轨迹线。 一主拉应力 回 一一一一主压应力 图41无腹筋梁的主应力分布 从主应力轨迹线可以看出,剪弯区段主拉应力方向是倾斜的,与梁轴线的交角约为45°, 而在梁的下边缘主拉应力方向接近于水平。在矩形截面梁中,主拉应力的数值是沿者某一条 主拉应力轨迹线自上向下逐步增大的。 混凝土的抗压强度较高,但其抗拉强度较低。在梁的剪弯段中,当主拉应力超过混凝 土的极限抗拉强度时,就会出现斜裂缝
4-1 第 4 章 受弯构件斜截面承载力计算 受弯构件在荷载作用下,各截面上除产生弯矩外,一般同时还有剪力。在受弯构件设 计中,首先应使构件的截面具有足够的抗弯承载力,即必须进行正截面抗弯承载力计算,这 在第 3 章中已介绍过。此外,在剪力和弯矩共同作用的区段,有可能发生沿斜截面的破坏, 故受弯构件还必须进行斜截面承载力计算。 本章主要讨论斜截面承载力的计算。 4.1 受弯构件斜截面的受力特点和破坏形态 在第 3 章受弯构件的构造中,介绍过钢筋混凝土梁设置的箍筋和弯起(斜)钢筋都起 抗剪作用。一般把箍筋和弯起(斜)钢筋统称为梁的腹筋。把配有纵向受力钢筋和腹筋的梁 称为有腹梁筋;而把仅有纵向受力钢筋而不设腹筋的梁称为无腹筋梁。在对受弯构件斜截面 受力分析中,为了便于探讨剪切破坏的特性,常以无腹筋梁为基础,再引伸到有腹筋梁。 4.1.1 无腹筋简支梁斜裂缝出现前后的受力状态 图 4-1 为一无腹筋简支梁,作用有两个对称的集中荷载。CD 段称为纯弯段;AC 段和 DB 段内的截面上既有弯矩 M 又有剪力 V,故称为剪弯段。 当梁上荷载较小时,裂缝尚未出现,钢筋和混凝土的应力-应变关系都处在弹性阶段, 所以,把梁近似看作匀质弹性体,可用材料力学方法来分析它的应力状态。 在剪弯区段截面上任一点都有剪应力和正应力存在,由单元体应力状态可知,它们的 共同作用将产生主拉应力 tp 和主压应力 cp ,图 4-1 即为这种情况下无腹筋简支梁的主应 力轨迹线。 ° ° ° 主拉应力 主压应力 图 4-1 无腹筋梁的主应力分布 从主应力轨迹线可以看出,剪弯区段主拉应力方向是倾斜的,与梁轴线的交角约为 45 , 而在梁的下边缘主拉应力方向接近于水平。在矩形截面梁中,主拉应力的数值是沿着某一条 主拉应力轨迹线自上向下逐步增大的。 混凝土的抗压强度较高,但其抗拉强度较低。在梁的剪弯段中,当主拉应力超过混凝 土的极限抗拉强度时,就会出现斜裂缝

梁的剪弯段出现斜裂缝后,截面的应力状态发生了质变,或者说发生了应力重分布。 这时,不能用材料力学公式来计算梁截面上的正应力和剪应力,因为这时梁已不再是完整的 匀质弹性梁了。 图4-2为一根出现斜裂缝后的无腹筋梁。现取左边五边形AA BCD隔离体[图4-2b)] 来分析它的平衡状态。在隔离体上,外荷载在斜截面AAB上引起的弯矩为M、剪力为VA, 而斜截面上的抵抗力则有:(1)斜截面上端混凝士剪压面(4A)上压力D和剪力C:(2) 纵向钢筋拉力T,:(3)在梁的变形过程中,斜裂缝的两边将发生相对剪切位移,使斜裂缝 面上产生摩擦力以及骨料凹凸不平相互间的骨料咬合力,它们的合力为S:(4)由于斜裂缝 两边有相对的上下错动,从而使纵向受拉钢筋受剪,通常称其为纵筋的销栓力 图42无腹筋梁出现斜裂缝后的隔离体图 a斜向裂缝b)隔离体 骨料咬合力和销栓力都难以定量估计,而且随斜裂缝的开展不断变化。为简化分析, S和a都不子考虑,根据平衡条件可写出: x=0 D =T Y=0 'a='c (4-1) ΣM=0 Va=T..: 由式(41)可以看出,斜裂缝出现后,梁内的应力状态有如下变化 (I)斜裂缝出现前,剪力a由梁全截面抵抗。但斜裂缝出现后,剪力V仅由截面AA (称剪压面或剪压区截面)抵抗,后者的面积远小于前者。所以,斜裂缝出现后,剪压区的 剪应力π显著增大:同时,剪压区的压应力σ也要增大。这是斜裂缝出现后应力重分布的一 个表现。 (2)斜裂缝出现前,截面BB处纵筋拉应力由截面BB处的弯矩M所决定,其值较 小。在斜裂缝出现后,截面BB处的纵筋拉应力则由截面AA处弯矩M决定。因M从远大 于,故纵筋拉应力显著增大,这是应力重分布的另一个表现。 4-2
4-2 梁的剪弯段出现斜裂缝后,截面的应力状态发生了质变,或者说发生了应力重分布。 这时,不能用材料力学公式来计算梁截面上的正应力和剪应力,因为这时梁已不再是完整的 匀质弹性梁了。 图 4-2 为一根出现斜裂缝后的无腹筋梁。现取左边五边形 AA ' BCD 隔离体[图 4-2b)] 来分析它的平衡状态。在隔离体上,外荷载在斜截面 AA ' B 上引起的弯矩为 MA、剪力为 VA, 而斜截面上的抵抗力则有:(1)斜截面上端混凝土剪压面(AA ' )上压力 DC和剪力 VC;(2) 纵向钢筋拉力 Ts ;(3)在梁的变形过程中,斜裂缝的两边将发生相对剪切位移,使斜裂缝 面上产生摩擦力以及骨料凹凸不平相互间的骨料咬合力,它们的合力为 Sa;(4)由于斜裂缝 两边有相对的上下错动,从而使纵向受拉钢筋受剪,通常称其为纵筋的销栓力 Vd。 ) ) 图 4-2 无腹筋梁出现斜裂缝后的隔离体图 a)斜向裂缝 b)隔离体 骨料咬合力和销栓力都难以定量估计,而且随斜裂缝的开展不断变化。为简化分析, Sa和 Vd 都不予考虑,根据平衡条件可写出: 0 0 0 = = = M Y x V a T z V V D T A s A C c s = = = (4-1) 由式(4-1)可以看出,斜裂缝出现后,梁内的应力状态有如下变化 (1)斜裂缝出现前,剪力 VA 由梁全截面抵抗。但斜裂缝出现后,剪力 VA 仅由截面 AA ' (称剪压面或剪压区截面)抵抗,后者的面积远小于前者。所以,斜裂缝出现后,剪压区的 剪应力 显著增大;同时,剪压区的压应力σ也要增大。这是斜裂缝出现后应力重分布的一 个表现。 (2)斜裂缝出现前,截面 BB ' 处纵筋拉应力由截面 BB ' 处的弯矩 MB 所决定,其值较 小。在斜裂缝出现后,截面 BB ' 处的纵筋拉应力则由截面 AA ' 处弯矩 MA 决定。因 MA 远大 于 MB,故纵筋拉应力显著增大,这是应力重分布的另一个表现

无腹筋梁相继出现斜裂缝后,斜裂缝的走向基本上是沿者主压应力轨迹线,主压应力 还能继续沿者斜裂缝之间的混凝土块传递(图43)。但是斜裂缝下部的拱形混凝士块体Ⅱ 图4-3无腹粱沿斜截面破坏的拱机理示意 所传递的主压应力,不能直接传递到支座上,它需通过纵向钢筋的销栓作用才能传递到支座 上。然而,纵筋所受的前力稍大就会使混凝土沿纵筋撕裂破坏,故纵筋销栓作用并不能充分 发挥,因此块体Ⅱ所传的力很小 主要依靠块体来传递主压应力。 这时 的受力状态可看 作 个设拉杆的拱结构,斜裂缝顶部的残余截面为拱顶,纵筋为拉杆拱顶至支座间的斜面 向受压混凝土为拱体。当拱顶的强度或拱体的抗压强度不足时,就会发生梁的截面破坏。这 就是无腹筋梁沿斜截面破坏的拱机理。 4.1.2无胺筋简支粱斜截面破坏形态 在讨论无腹筋简支梁斜截面破坏形态之前,有必要引出“剪跨比”的概念。剪跨比是 一个无量纲常数,用m= F亿来表示,此处M和V分别为剪弯区段中某个竖直截面的弯矩 和剪力,加为截面有效高度。一般把m的这个表达式称为“广义剪跨比”。对于集中荷载 作用下的简支梁(图41),则可用更为简便的形式来表达,例如图41中CC截面的剪跨比 m一,美中。为中力作用点支梁量近的支座之州的离,为 有时称m=行为“狭义剪跨比”。 试脸研究表明,随着剪跨比m的变化,无腹筋简支梁沿斜截面破坏的主要形态有以下 二种。 1)斜拉破坏[图4-4a)】 在荷载作用下,梁柔的剪跨段产生由梁底竖向的裂缝沿主压应力轨迹线向上延伸发展而 成的斜裂缝。其中有一条主要斜裂缝(又称临界斜裂缝)很快形成,并迅速伸展至荷载垫板 边缘而使梁体混凝土裂通,梁被撕裂成两部分而丧失承载力,同时,沿纵向钢筋往往伴随产 生水平撕裂裂缝。这种破坏称为斜拉破坏。这种破坏发生突然,破坏荷载等于或咯高于主要 斜裂缝出现时的荷载,破坏面较整齐,无混凝土压碎现象。 这种破坏往往发生于剪骑比较大(m>3)时 2)剪压破坏[图4-46)】 梁在剪弯区段内出现斜裂缝。随若荷载的增大,陆续出现几条斜裂缝,其中一条发展 成为临界斜裂缝。临界斜裂缝出现后,梁还能继续被增加荷载,而斜裂缝伸展至荷载垫板下
4-3 无腹筋梁相继出现斜裂缝后,斜裂缝的走向基本上是沿着主压应力轨迹线,主压应力 还能继续沿着斜裂缝之间的混凝土块传递(图 4-3)。但是斜裂缝下部的拱形混凝土块体 II 图 4-3 无腹梁沿斜截面破坏的拱机理示意 所传递的主压应力,不能直接传递到支座上,它需通过纵向钢筋的销栓作用才能传递到支座 上。然而,纵筋所受的剪力稍大就会使混凝土沿纵筋撕裂破坏,故纵筋销栓作用并不能充分 发挥,因此块体 II 所传的力很小,主要依靠块体 I 来传递主压应力。这时梁的受力状态可看 作是一个设拉杆的拱结构,斜裂缝顶部的残余截面为拱顶,纵筋为拉杆拱顶至支座间的斜面 向受压混凝土为拱体。当拱顶的强度或拱体的抗压强度不足时,就会发生梁的截面破坏。这 就是无腹筋梁沿斜截面破坏的拱机理。 4.1.2 无腹筋简支梁斜截面破坏形态 在讨论无腹筋简支梁斜截面破坏形态之前,有必要引出“剪跨比”的概念。剪跨比是 一个无量纲常数,用 Vh0 M m = 来表示,此处 M 和 V 分别为剪弯区段中某个竖直截面的弯矩 和剪力, h0 为截面有效高度。一般把 m 的这个表达式称为“广义剪跨比”。对于集中荷载 作用下的简支梁(图 4-1),则可用更为简便的形式来表达,例如图 4-1 中 CC ' 截面的剪跨比 0 h0 a V h M m C C = = ,其中 a 为集中力作用点至简支梁最近的支座之间的距离,称为“剪跨”。 有时称 h0 a m = 为“狭义剪跨比”。 试验研究表明,随着剪跨比 m 的变化,无腹筋简支梁沿斜截面破坏的主要形态有以下 三种。 1)斜拉破坏[图 4-4a)] 在荷载作用下,梁的剪跨段产生由梁底竖向的裂缝沿主压应力轨迹线向上延伸发展而 成的斜裂缝。其中有一条主要斜裂缝(又称临界斜裂缝)很快形成,并迅速伸展至荷载垫板 边缘而使梁体混凝土裂通,梁被撕裂成两部分而丧失承载力,同时,沿纵向钢筋往往伴随产 生水平撕裂裂缝。这种破坏称为斜拉破坏。这种破坏发生突然,破坏荷载等于或略高于主要 斜裂缝出现时的荷载,破坏面较整齐,无混凝土压碎现象。 这种破坏往往发生于剪跨比较大(m>3)时。 2)剪压破坏[图 4-4b)] 梁在剪弯区段内出现斜裂缝。随着荷载的增大,陆续出现几条斜裂缝,其中一条发展 成为临界斜裂缝。临界斜裂缝出现后,梁还能继续被增加荷载,而斜裂缝伸展至荷载垫板下, F
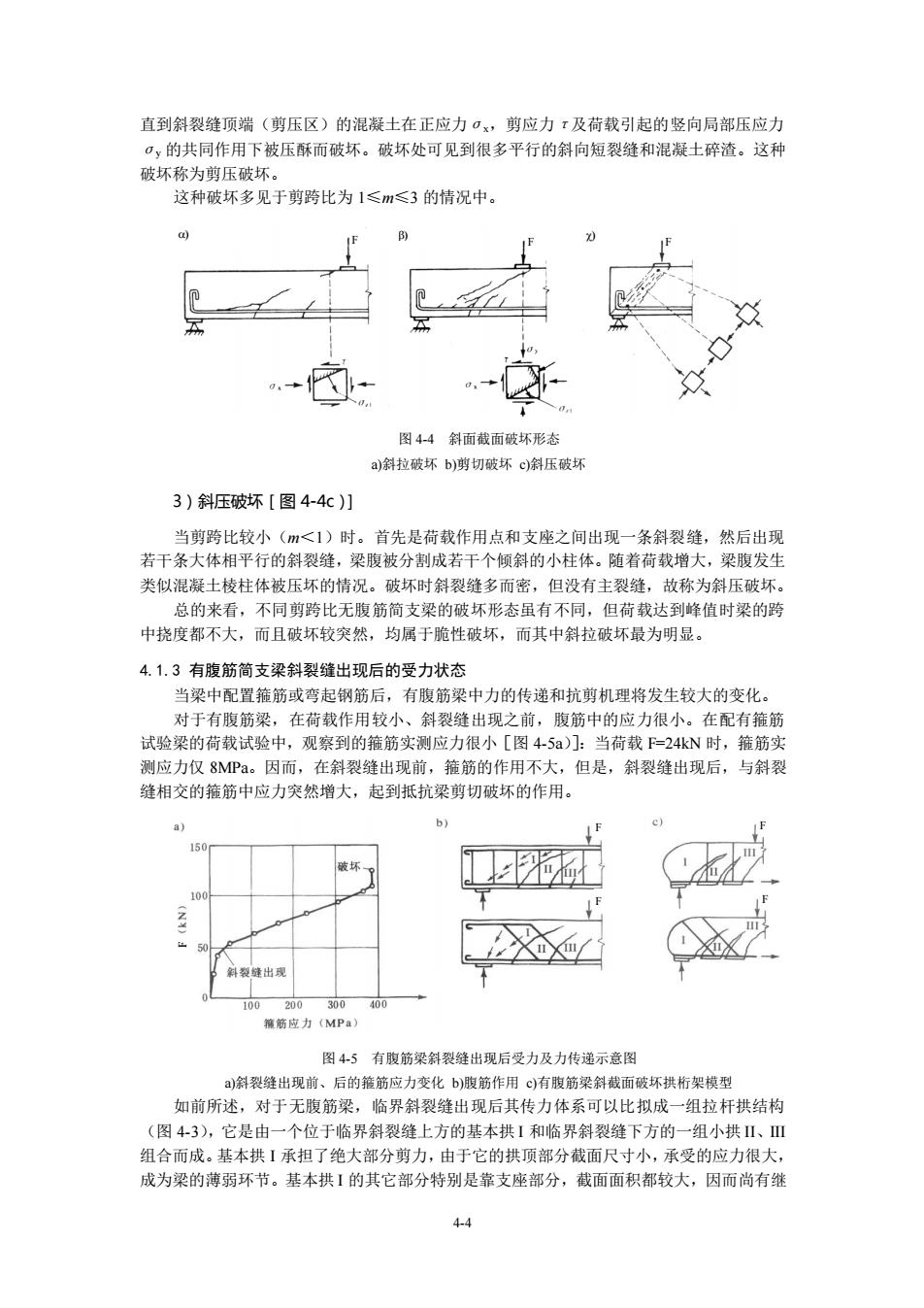
直到斜裂缝顶端(剪压区)的混凝土在正应力·,剪应力ī及荷载引起的竖向局部压应力 ·,的共同作用下被压酥而破坏。破坏处可见到很多平行的斜向短裂缝和混凝土碎渣。这种 破坏称为剪压破 这种破坏多见于剪跨比为1≤m≤3的情况中。 图44斜面截面破坏形态 )斜拉破坏b)谫切破坏c)斜压破坏 3)斜压破坏[图4-4c)】 当前跨比较小(<1)时。首先是荷载作用点和支座之间出现一条斜裂缝,然后出现 若干条大体相平行的斜裂缝,梁腹被分割成若干个倾斜的小柱体。随着荷载增大,梁腹发生 类似混凝土棱柱体被压坏的情况。破坏时斜裂缝多而密,但没有主裂缝,故称为斜压破坏 总的来看,不同剪跨比无腹筋简支梁的破坏形态虽有不同,但荷载达到峰值时梁的跨 中挠度都不大,而且破坏较突然,均属于脆性破坏,而其中斜拉破坏最为明显。 4.1.3有腹筋简支粱斜裂缝出现后的受力状态 当梁中配置箍筋或弯起钢筋后, 有腹筋梁中力的传递和抗剪机理将发生较大的变化, 对于有腹筋梁,在荷载作用较小、斜裂缝出现之前,腹筋中的应力很小。在配有箍筋 试验梁的荷载试验中,观察到的箍筋实测应力很小[图45a)]:当荷载F=24kN时,箍筋实 测应力仅8MP。因而,在斜裂缝出现前,箍筋的作用不大,但是,斜裂缝出现后,与斜裂 缝相交的箍筋中应力突然增大,起到抵抗梁剪切破坏的作用。 b) e) 藏筋应力(MPa) 图45有煦筋梁斜裂缝出现后受力及力传递示意图 )斜裂缝出现前、后的籍筋应力变化b)腹筋作用©有腹筋梁斜截面破坏拱桁架模型 如前所述,对于无腹筋梁,临界斜裂缝出现后其传力体系可以比拟成一组拉杆拱结构 (图43),它是由一个位于临界斜裂缝上方的基本拱1和临界斜裂缝下方的一组小拱Ⅱ、Ⅲ 组合而成。基本拱【承担了绝大部分剪力,由于它的拱顶部分截面尺寸小,承受的应力很大, 成为梁的黄弱环节。基本拱】的其它部分特别是靠支座部分,截面面积都较大,因而尚有 4.4
4-4 直到斜裂缝顶端(剪压区)的混凝土在正应力σx,剪应力τ及荷载引起的竖向局部压应力 σy 的共同作用下被压酥而破坏。破坏处可见到很多平行的斜向短裂缝和混凝土碎渣。这种 破坏称为剪压破坏。 这种破坏多见于剪跨比为 1≤m≤3 的情况中。 图 4-4 斜面截面破坏形态 a)斜拉破坏 b)剪切破坏 c)斜压破坏 3)斜压破坏[图 4-4c)] 当剪跨比较小(m<1)时。首先是荷载作用点和支座之间出现一条斜裂缝,然后出现 若干条大体相平行的斜裂缝,梁腹被分割成若干个倾斜的小柱体。随着荷载增大,梁腹发生 类似混凝土棱柱体被压坏的情况。破坏时斜裂缝多而密,但没有主裂缝,故称为斜压破坏。 总的来看,不同剪跨比无腹筋简支梁的破坏形态虽有不同,但荷载达到峰值时梁的跨 中挠度都不大,而且破坏较突然,均属于脆性破坏,而其中斜拉破坏最为明显。 4.1.3 有腹筋简支梁斜裂缝出现后的受力状态 当梁中配置箍筋或弯起钢筋后,有腹筋梁中力的传递和抗剪机理将发生较大的变化。 对于有腹筋梁,在荷载作用较小、斜裂缝出现之前,腹筋中的应力很小。在配有箍筋 试验梁的荷载试验中,观察到的箍筋实测应力很小[图 4-5a)]:当荷载 F=24kN 时,箍筋实 测应力仅 8MPa。因而,在斜裂缝出现前,箍筋的作用不大,但是,斜裂缝出现后,与斜裂 缝相交的箍筋中应力突然增大,起到抵抗梁剪切破坏的作用。 图 4-5 有腹筋梁斜裂缝出现后受力及力传递示意图 a)斜裂缝出现前、后的箍筋应力变化 b)腹筋作用 c)有腹筋梁斜截面破坏拱桁架模型 如前所述,对于无腹筋梁,临界斜裂缝出现后其传力体系可以比拟成一组拉杆拱结构 (图 4-3),它是由一个位于临界斜裂缝上方的基本拱 I 和临界斜裂缝下方的一组小拱 II、III 组合而成。基本拱 I 承担了绝大部分剪力,由于它的拱顶部分截面尺寸小,承受的应力很大, 成为梁的薄弱环节。基本拱 I 的其它部分特别是靠支座部分,截面面积都较大,因而尚有继 ) ) ) F F F F F F F F

续承载的潜力。其它小拱Ⅱ、Ⅲ所能传递的剪力很小,其实际具有的抗力并未得到充分发 挥。箍筋和斜筋的作用改变了这种情况,特别是箍筋的作用。在斜裂缝出现后,腹筋的作用 表现在(D把小拱体、Ⅲ向上拉住[图45b,使沿纵向钢筋的裂裂缝不发生,从 而使纵筋的销栓作用得以发挥,这样,小拱体川、就能更多地传递主压应力:(2)腹筋将 拱体Ⅱ、Ⅲ传递过来的主压应力,传到基本拱体1上断面尺寸较大的还有潜力的部位上去, 这就减轻了基本拱体I拱顶处所承压的应力,从而提高了梁的抗剪承载力:(3)腹筋能有效 地减小斜裂缝开展宽度,从而提高了斜截面上混凝土骨料咬合力。 腹筋将被斜裂缝分割的拱形混凝土块体牢固地连接在一起,但箍筋本身并不能把剪力 直接传递到支座上。在有腹筋梁中,筘筋、斜筋或弯起钢筋和斜裂缝之间的混凝土块体可比 拟成一个拱形桁架[图45)]。在拱形桁架模型中,基本拱体1视为拱形桁架的上弦压杆 拱体Ⅱ、Ⅲ是受压腹杆,纵向钢筋是下弦拉杆,箍筋等腹筋是受拉腹杆。 由上述有腹筋梁的抗剪机理分析可见,配置箍筋是提高梁抗剪承载力的有效措施。筛 筋一般是沿梁剪跨布置的,在梁的剪跨范围内只要出现斜裂缝,相应部位的箍筋就发挥作用。 弯起钢筋或斜筋只有与临界斜裂缝相交后才能发挥作用,可以提高梁的抗剪承载力。试验证 明,梁的抗剪承载力随弯筋面积的加大而提高,两者呈线性关系。弯筋仅在穿越斜裂缝的部 位才可能屈服。当弯筋恰好从斜裂缝顶端越过时,因接近受压区,弯筋有可能达不到屈服强 度,计算时要考虑这个因素。弯起钢筋虽能提高梁的抗剪承载力,但数量少而面积集中,对 限制大范围内的斜裂缝宽度的作用不大,所以,弯筋不宜单独使用,而总是与箍筋联合使用。 设置腹筋的简支梁斜截面剪切破坏形态与无腹筋简支梁一样,也概括为斜拉破坏、斜 压破坏和剪压破坏。但是,箍筋的配置数量对有腹筋梁的破坏形态有一定的影响,这在下节 详述。 4.2影响受弯构件斜截面抗剪能力的主要因素 试验研究表明,影响有腹筋梁斜截面抗剪能力的主要因素是剪跨比,混凝士强度、纵 向受拉钢筋配筋率和箍筋数量及强度等。 1)剪跨比m 前骑比m是影向受弯构件斜截面破坏形态和抗煎能力的主要因素。前骑比m实质上反 映了梁内正应力σ与剪应力t的相对比值。对弹性匀质材料的矩形截面简支梁,口和r可定 义为 a=a bhto M t=a bho 其中,a=%,/a,m=Mh。显然,m不同,则σ/r也不同,梁内主压应力迹线和主 拉应力迹线也是不同的(图46)。 5
4-5 续承载的潜力。其它小拱 II、III 所能传递的剪力很小,其实际具有的抗力并未得到充分发 挥。箍筋和斜筋的作用改变了这种情况,特别是箍筋的作用。在斜裂缝出现后,腹筋的作用 表现在:(1)把小拱体 II、III 向上拉住[图 4-5b)],使沿纵向钢筋的撕裂裂缝不发生,从 而使纵筋的销栓作用得以发挥,这样,小拱体 II、III 就能更多地传递主压应力;(2)腹筋 将 拱体 II、III 传递过来的主压应力,传到基本拱体 I 上断面尺寸较大的还有潜力的部位上去, 这就减轻了基本拱体 I 拱顶处所承压的应力,从而提高了梁的抗剪承载力;(3)腹筋能有效 地减小斜裂缝开展宽度,从而提高了斜截面上混凝土骨料咬合力。 腹筋将被斜裂缝分割的拱形混凝土块体牢固地连接在一起,但箍筋本身并不能把剪力 直接传递到支座上。在有腹筋梁中,箍筋、斜筋或弯起钢筋和斜裂缝之间的混凝土块体可比 拟成一个拱形桁架[图 4-5c)]。在拱形桁架模型中,基本拱体 I 视为拱形桁架的上弦压杆, 拱体 II、III 是受压腹杆,纵向钢筋是下弦拉杆,箍筋等腹筋是受拉腹杆。 由上述有腹筋梁的抗剪机理分析可见,配置箍筋是提高梁抗剪承载力的有效措施。箍 筋一般是沿梁剪跨布置的,在梁的剪跨范围内只要出现斜裂缝,相应部位的箍筋就发挥作用。 弯起钢筋或斜筋只有与临界斜裂缝相交后才能发挥作用,可以提高梁的抗剪承载力。试验证 明,梁的抗剪承载力随弯筋面积的加大而提高,两者呈线性关系。弯筋仅在穿越斜裂缝的部 位才可能屈服。当弯筋恰好从斜裂缝顶端越过时,因接近受压区,弯筋有可能达不到屈服强 度,计算时要考虑这个因素。弯起钢筋虽能提高梁的抗剪承载力,但数量少而面积集中,对 限制大范围内的斜裂缝宽度的作用不大,所以,弯筋不宜单独使用,而总是与箍筋联合使用。 设置腹筋的简支梁斜截面剪切破坏形态与无腹筋简支梁一样,也概括为斜拉破坏、斜 压破坏和剪压破坏。但是,箍筋的配置数量对有腹筋梁的破坏形态有一定的影响,这在下节 详述。 4.2 影响受弯构件斜截面抗剪能力的主要因素 试验研究表明,影响有腹筋梁斜截面抗剪能力的主要因素是剪跨比,混凝土强度、纵 向受拉钢筋配筋率和箍筋数量及强度等。 1)剪跨比 m 剪跨比 m 是影响受弯构件斜截面破坏形态和抗剪能力的主要因素。剪跨比 m 实质上反 映了梁内正应力σ与剪应力τ的相对比值。对弹性匀质材料的矩形截面简支梁,σ和τ可定 义为 0 2 2 0 1 bh V bh M = , = 3m = 其中, 3 1 2 = , m M Vh = 0 。显然,m 不同,则σ/τ也不同,梁内主压应力迹线和主 拉应力迹线也是不同的(图 4-6)
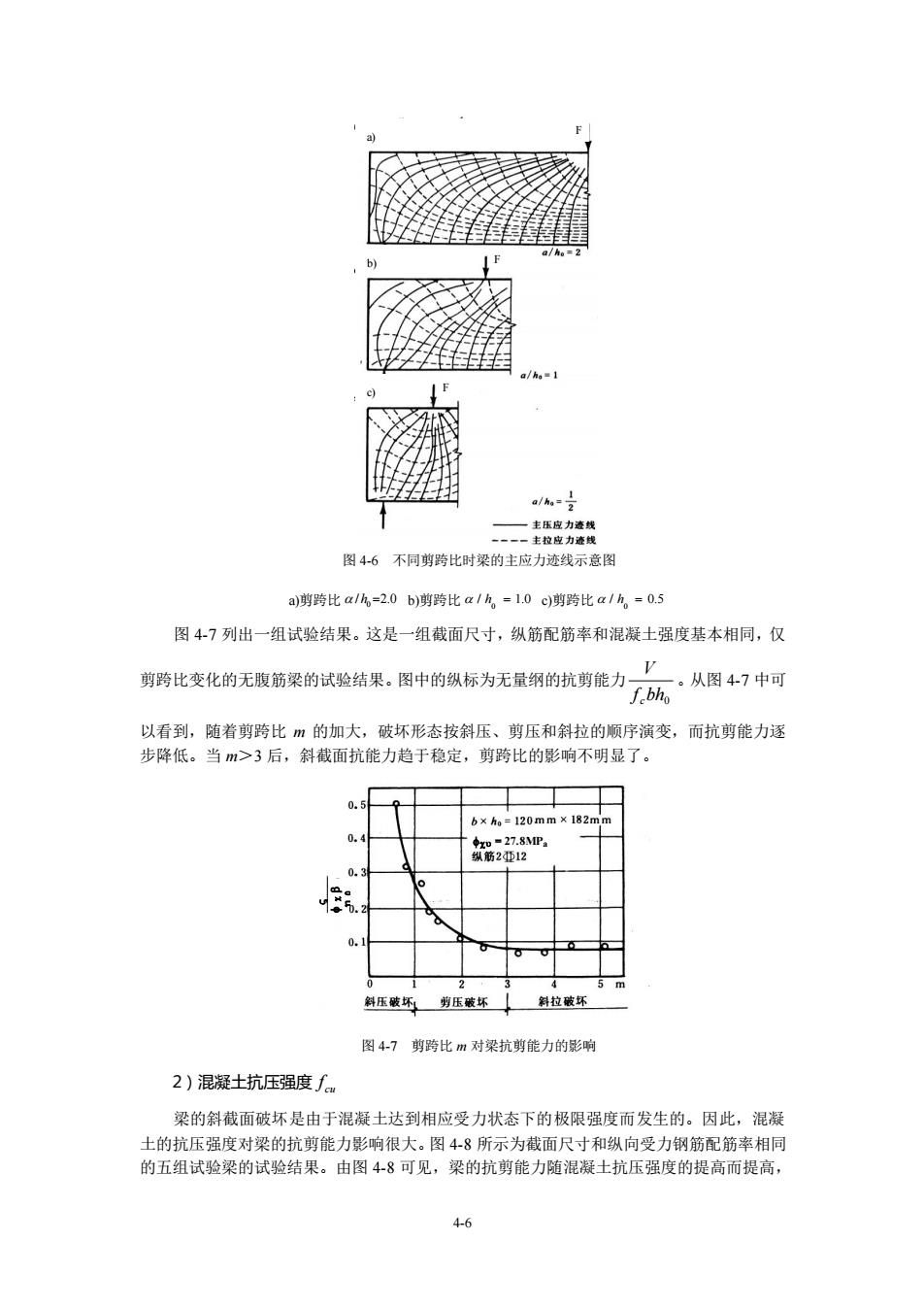
图46不同剪比时梁的主应力迹线示意图 a)蹲跨比a/%-20b)剪跨比a/%,-1.0c剪跨比a/%-0.5 图47列出一组试验结果。这是一组截面尺寸,纵筋配筋率和混凝土强度基本相同,仅 V 剪跨比变化的无腹筋梁的试验结果。图中的纵标为无量纲的抗剪能力 。从图47中可 以看到,随者剪跨比m的加大,破坏形态按斜压、剪压和斜拉的顺序演变,而抗剪能力逐 步降低。当m>3后,斜截面抗能力趋于稳定,剪跨比的影响不明显了。 b×h。=120 2 压乐剪压坏斜拉破坏 图4-7剪跨比m对梁抗剪能力的影响 2)混凝土抗压强度∫ 梁的斜截面破坏是由于混凝土达到相应受力状态下的极限强度而发生的。因此,混凝 土的抗压强度对梁的抗剪能力影响很大。图48所示为截面尺寸和纵向受力钢筋配筋率相同 的五组试验梁的试验结果。由图48可见,梁的抗剪能力随混凝土抗压强度的提高而提高, 4-6
4-6 图 4-6 不同剪跨比时梁的主应力迹线示意图 a)剪跨比 0 / 2.0 h = b)剪跨比 0 / 1.0 h = c)剪跨比 0 / 0.5 h = 图 4-7 列出一组试验结果。这是一组截面尺寸,纵筋配筋率和混凝土强度基本相同,仅 剪跨比变化的无腹筋梁的试验结果。图中的纵标为无量纲的抗剪能力 bh0 f V c 。从图 4-7 中可 以看到,随着剪跨比 m 的加大,破坏形态按斜压、剪压和斜拉的顺序演变,而抗剪能力逐 步降低。当 m>3 后,斜截面抗能力趋于稳定,剪跨比的影响不明显了。 图 4-7 剪跨比 m 对梁抗剪能力的影响 2)混凝土抗压强度 cu f 梁的斜截面破坏是由于混凝土达到相应受力状态下的极限强度而发生的。因此,混凝 土的抗压强度对梁的抗剪能力影响很大。图 4-8 所示为截面尺寸和纵向受力钢筋配筋率相同 的五组试验梁的试验结果。由图 4-8 可见,梁的抗剪能力随混凝土抗压强度的提高而提高, a) b) c) = 27.8MPa F F F
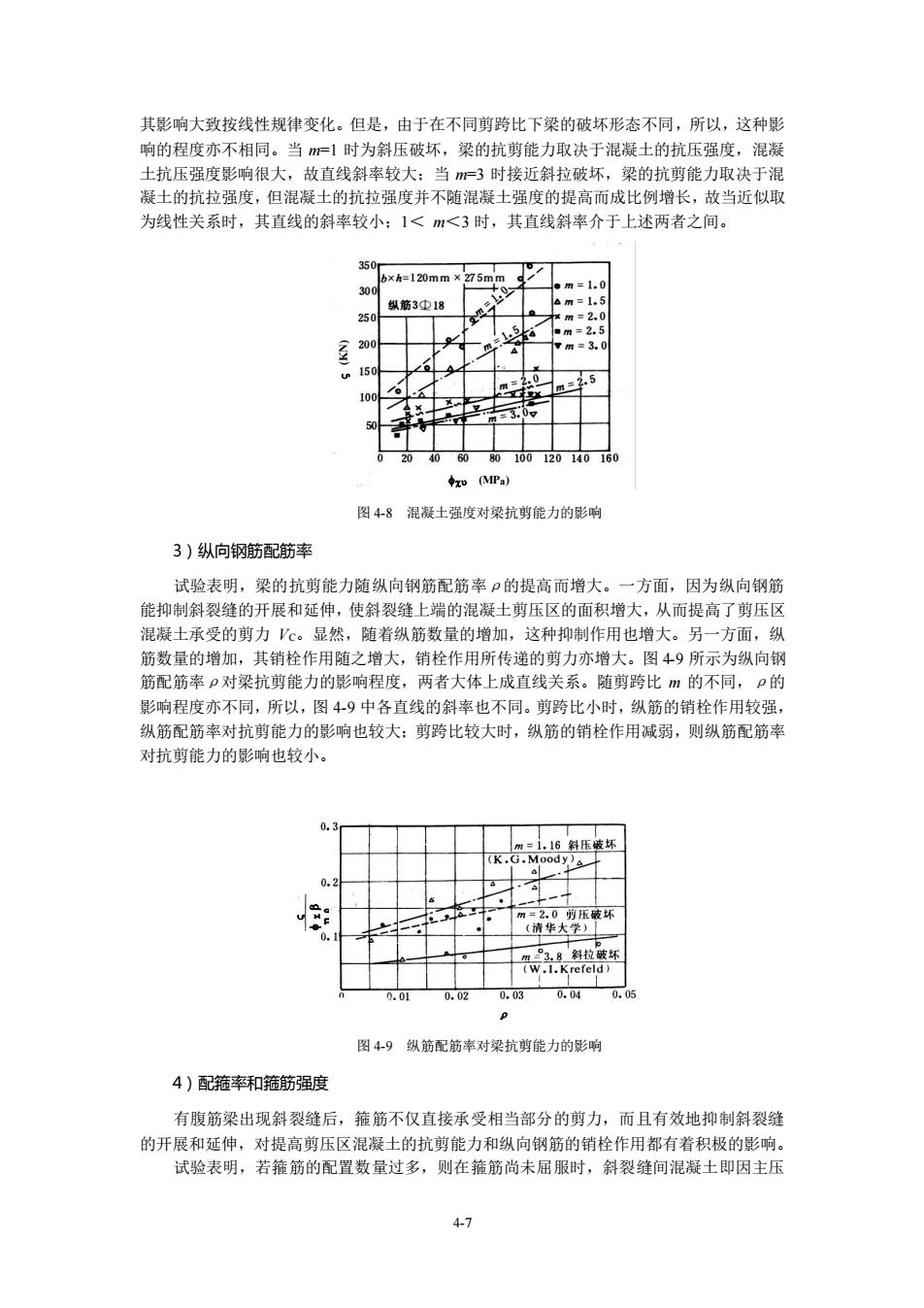
其影响大致按线性规律变化。但是,由于在不同剪跨比下梁的破坏形态不同,所以,这种影形 响的程度亦不相同。当1时为斜压破坏,梁的抗剪能力取决于混凝士的抗压强度,混 士抗压强度影响很大 故直线斜率较大:当m3时接近斜拉破坏,梁的抗剪能力取决于混 凝土的抗拉强度,但混凝士的抗拉强度并不随混凝士强度的提高而成比例增长,故当近似取 为线性关系时,其直线的斜*较小:1<m<3时,其直线斜率介于上述两者之间。 50 b×h=120mm×275mn 000204010 图48混凝土强度对梁抗剪能力的影响 3)纵向钢筋配筋率 试验表明,梁的抗剪能力随纵向钢筋配筋率ρ的提高而增大。一方面,因为纵向钢筋 能抑制斜裂缝的开展和延伸,使斜裂缝上端的混凝土剪压区的面积增大,从而提高了剪压区 混凝土承受的剪力。显然,随着纵筋数量的增加,这种抑制作用也增大。另一方面,纵 饰勒量的增加,其销栓作用随之瑞大,销栓作用所估递的前力亦增大。图49所示为纵向钢 筋配筋率P对梁抗剪能力的影响程度,两者大体上成直线关系。 随剪跨比m的不同, P的 影响程度亦不同,所以,图49中各直线的斜率也不同。剪跨比小时,纵筋的销栓作用较强 纵筋配筋率对抗剪能力的影响也较大:剪跨比较大时,纵筋的销栓作用减弱,则纵筋配筋率 对抗剪能力的影响也较小。 1.16斜压坏 请华大 8 .01 0.03 0, 图49纵筋配筋率对梁抗剪能力的影响 4)配籍率和箍筋强度 有腹筋梁出现斜裂缝后,箍筋不仅直接承受相当部分的剪力,而且有效地抑制斜裂缝 的开展和延伸,对提高剪压区混凝土的抗剪能力和纵向钢筋的销栓作用都有着积极的影响。 试验表明,若箍筋的配置数量过多,则在箍筋尚未屈服时,斜裂缝间混凝士即因主压 41
4-7 其影响大致按线性规律变化。但是,由于在不同剪跨比下梁的破坏形态不同,所以,这种影 响的程度亦不相同。当 m=1 时为斜压破坏,梁的抗剪能力取决于混凝土的抗压强度,混凝 土抗压强度影响很大,故直线斜率较大;当 m=3 时接近斜拉破坏,梁的抗剪能力取决于混 凝土的抗拉强度,但混凝土的抗拉强度并不随混凝土强度的提高而成比例增长,故当近似取 为线性关系时,其直线的斜率较小;1< m<3 时,其直线斜率介于上述两者之间。 图 4-8 混凝土强度对梁抗剪能力的影响 3)纵向钢筋配筋率 试验表明,梁的抗剪能力随纵向钢筋配筋率ρ的提高而增大。一方面,因为纵向钢筋 能抑制斜裂缝的开展和延伸,使斜裂缝上端的混凝土剪压区的面积增大,从而提高了剪压区 混凝土承受的剪力 VC。显然,随着纵筋数量的增加,这种抑制作用也增大。另一方面,纵 筋数量的增加,其销栓作用随之增大,销栓作用所传递的剪力亦增大。图 4-9 所示为纵向钢 筋配筋率ρ对梁抗剪能力的影响程度,两者大体上成直线关系。随剪跨比 m 的不同,ρ的 影响程度亦不同,所以,图 4-9 中各直线的斜率也不同。剪跨比小时,纵筋的销栓作用较强, 纵筋配筋率对抗剪能力的影响也较大;剪跨比较大时,纵筋的销栓作用减弱,则纵筋配筋率 对抗剪能力的影响也较小。 图 4-9 纵筋配筋率对梁抗剪能力的影响 4)配箍率和箍筋强度 有腹筋梁出现斜裂缝后,箍筋不仅直接承受相当部分的剪力,而且有效地抑制斜裂缝 的开展和延伸,对提高剪压区混凝土的抗剪能力和纵向钢筋的销栓作用都有着积极的影响。 试验表明,若箍筋的配置数量过多,则在箍筋尚未屈服时,斜裂缝间混凝土即因主压 (KN) (MPa) ρ

应力过大而发生斜压破坏。此时梁的抗剪能力取决于构件的截面尺寸和混凝士强度,并与无 腹筋梁斜压破坏时的抗剪能力相接近。 若箍筋的配置数量远 斜裂缝出现后,原来由混凝土承受的拉力转由与斜裂缝相 交的箍筋承受,在箍筋尚未屈服时,由于箍筋的作用,延缓和限制了斜裂缝的开展和延伸 承载力尚能有较大的增长。当箍筋屈服后,其变形迅速增大,不再能有效地抑制斜裂缝的开 展和延伸,最后,斜裂缝上端的混凝土在剪、压复合应力作用下达到极限强度,发生剪压破 坏。此时,梁的抗剪能力主要与混凝土强度和箍筋配置数量有关,而剪跨比和纵筋配筋率等 因素的影响相对较 若箍筋配置数量过少,则斜裂缝一出现,截面即发生急剧的应力重分布 原来由混凝 土承受的拉力转由箍筋承受,使箍筋很快达到屈服,变形剧增,不能抑制斜裂缝的开展,此 时梁的破坏形态与无腹筋梁相似。当剪跨比较大时,也将产生脆性的斜拉破坏。 箍筋用量一般用箍筋配筋率(工程上习惯称配箍率)P(%)表示,即 (4-2) 式中A。一一斜截面内配置在沿梁长度方向一个箍筋间矩3,范围内的箍筋各肢总截面积: b一一截面宽度,对T形裁面梁取b为肋宽: S,一一沿梁长度方向箍筋的间距 图410表示配箍率与箍筋抗拉强度的乘积对梁抗剪能力的影响。当其它条件相同时, 两者大体成线性关系。 由于梁斜截面破坏属于脆性破坏,为了提高斜截面延性,不宜采用高强钢筋作箍筋。 (MPa) 图410配箍率对梁抗剪能力的影响 4.3受弯构件的斜截面抗剪承载力 加前所述,钢筋混土梁沿斜截面的主要破坏形态有斜压破坏、斜拉破坏和前压破坏 面抗剪承载力 的计算。《公路桥规》的基本公式就是针对这种破坏形态的受力特征而建立的。 4.3.1斜截面抗剪承载力计算的基本公式及适用条件 4-8
4-8 应力过大而发生斜压破坏。此时梁的抗剪能力取决于构件的截面尺寸和混凝土强度,并与无 腹筋梁斜压破坏时的抗剪能力相接近。 若箍筋的配置数量适当,则斜裂缝出现后,原来由混凝土承受的拉力转由与斜裂缝相 交的箍筋承受,在箍筋尚未屈服时,由于箍筋的作用,延缓和限制了斜裂缝的开展和延伸, 承载力尚能有较大的增长。当箍筋屈服后,其变形迅速增大,不再能有效地抑制斜裂缝的开 展和延伸,最后,斜裂缝上端的混凝土在剪、压复合应力作用下达到极限强度,发生剪压破 坏。此时,梁的抗剪能力主要与混凝土强度和箍筋配置数量有关,而剪跨比和纵筋配筋率等 因素的影响相对较小。 若箍筋配置数量过少,则斜裂缝一出现,截面即发生急剧的应力重分布,原来由混凝 土承受的拉力转由箍筋承受,使箍筋很快达到屈服,变形剧增,不能抑制斜裂缝的开展,此 时梁的破坏形态与无腹筋梁相似。当剪跨比较大时,也将产生脆性的斜拉破坏。 箍筋用量一般用箍筋配筋率(工程上习惯称配箍率) sv (%)表示,即 v sv sv bS A = (4-2) 式中 Asv ——斜截面内配置在沿梁长度方向一个箍筋间矩 v s 范围内的箍筋各肢总截面积; b ——截面宽度,对 T 形截面梁取 b 为肋宽; v S ——沿梁长度方向箍筋的间距。 图 4-10 表示配箍率与箍筋抗拉强度的乘积对梁抗剪能力的影响。当其它条件相同时, 两者大体成线性关系。 由于梁斜截面破坏属于脆性破坏,为了提高斜截面延性,不宜采用高强钢筋作箍筋。 图 4-10 配箍率对梁抗剪能力的影响 4.3 受弯构件的斜截面抗剪承载力 如前所述,钢筋混凝土梁沿斜截面的主要破坏形态有斜压破坏、斜拉破坏和剪压破坏 等。在设计时,对于斜压和斜拉破坏,一般是采用截面限制条件和一定的构造措施予以避免。 对于常见的剪压破坏形态,梁的斜截面抗剪力变化幅度较大,故必须进行斜截面抗剪承载力 的计算。《公路桥规》的基本公式就是针对这种破坏形态的受力特征而建立的。 4.3.1 斜截面抗剪承载力计算的基本公式及适用条件 =34MPa ρ

配有箍筋和弯起钢筋的钢筋混凝土梁,当发生剪压破坏时,其抗剪承载力人。是由剪压 区混凝土抗剪力,箍筋所能承受的剪力V和弯起钢筋所能承受的剪力V。所组成(图 411),即 V=V+V+Vs (43) 飞nfV an v da 图4+1斜面抗剪承载力计算图式 在有腹筋梁中,箍筋的存在抑制了斜裂缝的开展,使剪压区面积增大,导致了剪压区 混凝土抗剪能力的提高,其提高程度与箍筋的抗拉强度和配箍率有关。因而,式(4-3)中 的V。与V,是紧密相关的,但两者目前尚无法分别予以精确定量,而只能用V来表达混凝 土和箍筋的综合抗剪承载力,即 (4-4) 《公路桥规》根据国内外的有关试验资料,对配有腹筋的钢筋混凝土梁斜截面抗剪承 载力的计算采用下述半经验半理论的公式: YoVV=aaza(0.45x10)bh(2+0.6p)fpf +0.75x10-3)fΣAsn6, (45) 式中 V。一一斜截面受压端正截面上由作用(或荷载)效应所产生的最大剪力组合 设计值(kN): Y。一一桥梁结构的重要性系数 一一异号弯矩影响系数。计算简支梁和连续梁近边支点梁段的抗剪承载力时, =1.0:计算连续梁和悬臂梁近中间支点梁段的抗剪承载力时,0.9: 一一预应力提高系数(详见第13章)。对钢筋混凝土受弯构件,,=1: a -一受压翼缘的影响系数。对具有受压翼缘的截面,取心,=1.1: b 斜截面受压区顶端截面处矩形截面宽度(mm),或T形和I形裁面腹板究 度(mm: h,一一斜截面受压端正截面上的有效高度,自纵向受拉钢筋合力点到受压边缘的 距离(mm): 4-9
4-9 配有箍筋和弯起钢筋的钢筋混凝土梁,当发生剪压破坏时,其抗剪承载力 Vu 是由剪压 区混凝土抗剪力 Vc,箍筋所能承受的剪力 Vsv 和弯起钢筋所能承受的剪力 Vsb 所组成(图 4-11),即 Vu =Vc +Vsv +Vsb (4-3) 图 4-11 斜截面抗剪承载力计算图式 在有腹筋梁中,箍筋的存在抑制了斜裂缝的开展,使剪压区面积增大,导致了剪压区 混凝土抗剪能力的提高,其提高程度与箍筋的抗拉强度和配箍率有关。因而,式(4-3)中 的 Vc与 Vsv是紧密相关的,但两者目前尚无法分别予以精确定量,而只能用 Vcs 来表达混凝 土和箍筋的综合抗剪承载力,即 Vu =Vcs +Vsb (4-4) 《公路桥规》根据国内外的有关试验资料,对配有腹筋的钢筋混凝土梁斜截面抗剪承 载力的计算采用下述半经验半理论的公式: 0Vd ≤ ( ) ( ) 3 1 2 3 0 , 0.45 10 2 0.6 V bh p f f u cu k sv sv − = + ( ) sd Asb s 0.75 10 f sin 3 + − (4-5) 式中 V d ——斜截面受压端正截面上由作用(或荷载)效应所产生的最大剪力组合 设计值(kN); 0 ——桥梁结构的重要性系数; 1 ——异号弯矩影响系数。计算简支梁和连续梁近边支点梁段的抗剪承载力时, 1 =1.0;计算连续梁和悬臂梁近中间支点梁段的抗剪承载力时, 1 =0.9; 2 ——预应力提高系数(详见第 13 章)。对钢筋混凝土受弯构件, 2 =1; 3 ——受压翼缘的影响系数。对具有受压翼缘的截面,取 3 =1.1; b ——斜截面受压区顶端截面处矩形截面宽度(mm),或 T 形和 I 形截面腹板宽 度(mm); 0 h ——斜截面受压端正截面上的有效高度,自纵向受拉钢筋合力点到受压边缘的 距离(mm);

p一一斜截面内纵向受拉钢筋的配筋率,p=100p,p=A/bh,当p>2.5 时,取p=2.5: ∫一一混凝土立方体抗压强度标准值(MPa): P,—箍筋配筋率,见式(4-2): 厂—箍筋抗拉强度设计值(MPa): ∫a一一弯起钢筋的抗拉强度设计值(MPa): A,。一斜截面内在同一个弯起钢筋平面内的弯起钢筋总截面面积(mm): 日,一一弯起钢筋的切线与构件水平纵向轴线的夹角。 这里要指出以下几点: (1)式(45)所表达的斜截面抗剪承载力中,混凝土和箍筋提供的综合抗剪承载力为 V。=aa,a,(0.45×10)(2+0.6p)V厂Pnfn,弯起钢筋提供的抗剪承载力为 V=0.75×103)/aΣ4,sn0,。当不设弯起钢筋时,梁的斜截面抗剪力Y,等于V。。 (2)式(45)是一个半经验半理论公式,使用时必须按规定的单位代入数值,而计算 得到的斜截面抗剪承载力V的单位为kN。 式(45)是根据剪压破坏形态发生时的受力特征和试验资料而制定的,仅在一定的条 件下才适用,因而必须限定其适用范围,称为计算公式的上、下限值。 1)上限值—截面最小尺寸 当梁的截面尺寸较小而剪力过大时,就可能在梁的肋部产生过大的主压应力,使梁发生 斜压破坏(或梁肋板压坏)。这种梁的抗剪承载力取决于混凝士的抗压强度及梁的截面尺寸 不能用增加腹筋数量来提高抗剪承载力。《公路桥规》规定了截面最小尺寸的限制条件,这 种限制,同时也为了防止梁在使用阶段斜裂缝开展过大,特别是薄腹梁。截面尺寸应满足: y'a≤0.51×10-fnxbh (kN) (4-6) 式中V。一一验算截面处由作用(或荷载)产生的剪力组合设计值(kN): ∫一一混凝土立方体抗压强度标准值(MPa): b一一相应于剪力组合设计值处矩形截面的宽度(mm),或T形和1形截面腹板宽 度(mm): 么一一相应于剪力组合设计值处截面的有效高度(mm)。 若式(4-6)不满足,则应加大截面尺寸或提高混凝土强度等级。 2)下限值—按构造要求配置箍筋 4.10
4-10 p ——斜截面内纵向受拉钢筋的配筋率, p =100 , = A bh s 0 ,当 p >2.5 时,取 p =2.5; cu k f , ——混凝土立方体抗压强度标准值(MPa); sv ——箍筋配筋率,见式(4-2); sv f ——箍筋抗拉强度设计值(MPa); sd f ——弯起钢筋的抗拉强度设计值(MPa); Asb ——斜截面内在同一个弯起钢筋平面内的弯起钢筋总截面面积(mm2); s ——弯起钢筋的切线与构件水平纵向轴线的夹角。 这里要指出以下几点: (1)式(4-5)所表达的斜截面抗剪承载力中,混凝土和箍筋提供的综合抗剪承载力为 ( ) ( ) 3 1 2 3 , 0.45 10 2 0.6 V p f f cs cu k sv sv − = + ,弯起钢筋 提 供的 抗 剪 承 载力 为 ( ) sb sd Asb s V 0.75 10 f sin 3 = − 。当不设弯起钢筋时,梁的斜截面抗剪力 Vu 等于 Vcs 。 (2)式(4-5)是一个半经验半理论公式,使用时必须按规定的单位代入数值,而计算 得到的斜截面抗剪承载力 Vu 的单位为 kN。 式(4-5)是根据剪压破坏形态发生时的受力特征和试验资料而制定的,仅在一定的条 件下才适用,因而必须限定其适用范围,称为计算公式的上、下限值。 1)上限值——截面最小尺寸 当梁的截面尺寸较小而剪力过大时,就可能在梁的肋部产生过大的主压应力,使梁发生 斜压破坏(或梁肋板压坏)。这种梁的抗剪承载力取决于混凝土的抗压强度及梁的截面尺寸, 不能用增加腹筋数量来提高抗剪承载力。《公路桥规》规定了截面最小尺寸的限制条件,这 种限制,同时也为了防止梁在使用阶段斜裂缝开展过大,特别是薄腹梁。截面尺寸应满足: 0Vd ≤ ( ) , 0 3 0.51 10 f cu k bh − (kN) (4-6) 式中 Vd ——验算截面处由作用(或荷载)产生的剪力组合设计值(kN); cu k f , ——混凝土立方体抗压强度标准值(MPa); b ——相应于剪力组合设计值处矩形截面的宽度(mm),或 T 形和 I 形截面腹板宽 度(mm); 0 h ——相应于剪力组合设计值处截面的有效高度(mm)。 若式(4-6)不满足,则应加大截面尺寸或提高混凝土强度等级。 2)下限值——按构造要求配置箍筋