
第5章受扭构件承载力计算 弯梁桥和斜梁(板)桥是高等公路和城市道路常用的桥梁。钢筋混凝士弯柔、斜梁(板), 即使不考虑活荷载,仅在恒载作用下,梁的截面上除有弯矩M、剪力V外,还存在若扭矩T (图5.1)。 图51曲线梁示意图 由于扭矩、弯矩和剪力的作用,构件的截面上将产生相应的主拉应力。当主拉应力超过 混凝土的抗拉强度时,构件便会开裂。因此,必须配置适量的钢筋(纵筋和箍筋)来限制裂 缝的开展和提高钢筋混凝土构件的承载能力 在实际工程中,纯扭构件并不常见,较多出现的是弯矩、扭矩和剪力共同作用的构件 由于弯、扭、剪共同作用的相互影响,使得构件的受力状况非常复杂。而纯扭是研究弯扭构 件受力的基础,只有对纯扭构件有深入的了解,才能对弯、扭、剪共同作用下结构的破坏机 理作进一步的分析和研究,也才能对构件进行比较合理的配筋。因此,本章的介绍将从纯扭 构件开始。 5.1纯扭构件的破坏特征和承载力计算 图5-2为配置箍筋和纵筋的钢筋混凝土受扭构件,从加载直到破环全过程的扭矩T和扭 转角日的关系曲线。由图5-2可见,加载初期截面扭转变形很小,其性能与素混凝土受扭构 件相似。当斜裂缝出现以后,由于混凝土部分卸载,钢筋应力明品增大,扭转角加大,扭转 刚度明显降低,在T-日曲线上出现水平段。当扭转角增加到一定值后,钢筋应变趋于稳定 形成新的受力状态。当继续施加荷载时,变形增长较快,裂缝的数量逐步增多,裂缝宽度逐 T 图5-2钢筋混凝士受扭构件的下0曲线 渐加大,构件的四个面上形成连续的或不连续的与构件纵轴线成某个角度的螺旋形裂缝(图 5-3)。这时T-日关系大体还是呈直线变化 当荷载接近极限扭转矩时,在构件截面长边 的斜裂缝中,有一条发展为临界裂缝,与这条空间斜裂缝相交的部分箍筋(长肢)或部分纵 筋将首先屈服,产生较大的非弹性变形,这时T-日曲线趋于水平。到达极限扭矩时,和临 界斜裂缝相交的箍筋短肢及纵向钢筋相继屈服,但没有与临界斜裂缝相交的箍筋和纵筋并没 5-1
5-1 第 5 章 受扭构件承载力计算 弯梁桥和斜梁(板)桥是高等公路和城市道路常用的桥梁。钢筋混凝土弯梁、斜梁(板), 即使不考虑活荷载,仅在恒载作用下,梁的截面上除有弯矩 M、剪力 V 外,还存在着扭矩 T (图 5-1)。 图 5-1 曲线梁示意图 由于扭矩、弯矩和剪力的作用,构件的截面上将产生相应的主拉应力。当主拉应力超过 混凝土的抗拉强度时,构件便会开裂。因此,必须配置适量的钢筋(纵筋和箍筋)来限制裂 缝的开展和提高钢筋混凝土构件的承载能力。 在实际工程中,纯扭构件并不常见,较多出现的是弯矩、扭矩和剪力共同作用的构件。 由于弯、扭、剪共同作用的相互影响,使得构件的受力状况非常复杂。而纯扭是研究弯扭构 件受力的基础,只有对纯扭构件有深入的了解,才能对弯、扭、剪共同作用下结构的破坏机 理作进一步的分析和研究,也才能对构件进行比较合理的配筋。因此,本章的介绍将从纯扭 构件开始。 5.1 纯扭构件的破坏特征和承载力计算 图 5-2 为配置箍筋和纵筋的钢筋混凝土受扭构件,从加载直到破坏全过程的扭矩 T 和扭 转角 的关系曲线。由图 5-2 可见,加载初期截面扭转变形很小,其性能与素混凝土受扭构 件相似。当斜裂缝出现以后,由于混凝土部分卸载,钢筋应力明显增大,扭转角加大,扭转 刚度明显降低,在 T - 曲线上出现水平段。当扭转角增加到一定值后,钢筋应变趋于稳定 形成新的受力状态。当继续施加荷载时,变形增长较快,裂缝的数量逐步增多,裂缝宽度逐 开裂 纵筋或箍筋屈服 纵筋和箍筋全屈服 混凝土破坏 图 5-2 钢筋混凝土受扭构件的 T-θ曲线 渐加大,构件的四个面上形成连续的或不连续的与构件纵轴线成某个角度的螺旋形裂缝(图 5-3)。这时 T - 关系大体还是呈直线变化。当荷载接近极限扭转矩时,在构件截面长边上 的斜裂缝中,有一条发展为临界裂缝,与这条空间斜裂缝相交的部分箍筋(长肢)或部分纵 筋将首先屈服,产生较大的非弹性变形,这时 T - 曲线趋于水平。到达极限扭矩时,和临 界斜裂缝相交的箍筋短肢及纵向钢筋相继屈服,但没有与临界斜裂缝相交的箍筋和纵筋并没

有屈服。由于这时斜裂缝宽度已很大,混凝土在逐步退出工作,故构件的抵抗扭矩开始逐步 下降,最后在构件的另一长边出现了压区塑性铰线或出现两个裂缝间混凝士被压碎的现象时 构件破坏 图53扭转裂缝分布图 综上所述,钢筋混凝士构件抗扭性能的两个重要衡量指标是:(1)构件的开裂扭矩:(2) 构件的破坏扭矩。 5.1.1矩形截面纯扭构件的开裂扭矩 钢筋混凝土受扭构件开裂前钢筋中的应力很小,钢筋对开裂扭矩的影响不大,因此,可 以忽路钢筋对开裂扭矩的影响,将构件作为纯混疑土受扭构件来处理开裂扭矩的问题。 图5钜形雄面纯知构件 图54为矩形截面的纯扭构件。在扭矩作用下,由材料力学可知,匀质弹性材料的矩形 截面构件截面的剪应力分布如图5-5),截面长边中点的剪应力最大。根据力的平衡可知主 拉应力0,。=T,主拉应力的方向与构件轴线成0=45°角。当主拉应力o超过混凝土的 抗拉强度∫时,混凝土将在垂直于主拉应力的方向开裂,在纯扭作用下,构件裂缝总是沿 与构件纵轴成0=45°方向发展且开裂扭矩即为主拉应力p=t=∫,时的扭矩。因为混凝 土不是理想的弹性材料,故按上述计算图式来计算混凝士构件的开裂扭矩是偏低的。 假设为理想塑性材料的矩形截面构件,截面上某一点应力达到材料的屈服强度时,只意 味若局部材料开始进入塑性状态,此时构件仍能珠续承担荷载。直到截面上的应力全部达到 材料的屈服强度时,构件才能达到其极限承载能力,此时,截面上剪应力的分布如图5-5b): 现按图5b)所示理想塑性材料的剪应力分布求其抵抗扭矩。假定钢筋 牛矩开 截面进入全塑性状态时,出现与截面各边成45”的剪应力界限分布区,形成的剪应力达到 极限值t,t=t=∫a,剪力流对截面的扭矩中心取矩,由平衡条件可得到 T-2-创+42-创 -(6h-6r=形 (5-1) 52
5-2 有屈服。由于这时斜裂缝宽度已很大,混凝土在逐步退出工作,故构件的抵抗扭矩开始逐步 下降,最后在构件的另一长边出现了压区塑性铰线或出现两个裂缝间混凝土被压碎的现象时 构件破坏。 裂缝 图 5-3 扭转裂缝分布图 综上所述,钢筋混凝土构件抗扭性能的两个重要衡量指标是:(1)构件的开裂扭矩;(2) 构件的破坏扭矩。 5.1.1 矩形截面纯扭构件的开裂扭矩 钢筋混凝土受扭构件开裂前钢筋中的应力很小,钢筋对开裂扭矩的影响不大,因此,可 以忽略钢筋对开裂扭矩的影响,将构件作为纯混凝土受扭构件来处理开裂扭矩的问题。 图 5-4 矩形截面纯扭构件 图 5-4 为矩形截面的纯扭构件。在扭矩作用下,由材料力学可知,匀质弹性材料的矩形 截面构件截面的剪应力分布如图 5-5a),截面长边中点的剪应力最大。根据力的平衡可知主 拉应力 t p = ,主拉应力的方向与构件轴线成 = 45°角。当主拉应力 tp 超过混凝土的 抗拉强度 t f 时,混凝土将在垂直于主拉应力的方向开裂,在纯扭作用下,构件裂缝总是沿 与构件纵轴成 = 45°方向发展且开裂扭矩即为主拉应力 t p = = t f 时的扭矩。因为混凝 土不是理想的弹性材料,故按上述计算图式来计算混凝土构件的开裂扭矩是偏低的。 假设为理想塑性材料的矩形截面构件,截面上某一点应力达到材料的屈服强度时,只意 味着局部材料开始进入塑性状态,此时构件仍能继续承担荷载。直到截面上的应力全部达到 材料的屈服强度时,构件才能达到其极限承载能力,此时,截面上剪应力的分布如图 5-5b)。 现按图 5-5b)所示理想塑性材料的剪应力分布求其抵抗扭矩。假定钢筋混凝土构件矩形 截面进入全塑性状态时,出现与截面各边成 45°的剪应力界限分布区,形成的剪应力达到 极限值 max , td = = f max ,剪力流对截面的扭矩中心取矩,由平衡条件可得到 ( ) ( ) max 1 2 1 2 4 2 2 4 2 2 2 3 2 2 3 2 2 b b b b b b b b T h b h b = − + + + − ( ) 2 max max 3 6 t b = − = h b W (5-1)

图55矩形截而纯扭构件剪应力分布 弹性状态剪应力分布b)塑性状态剪应力分布 但是混凝土既非弹性材料,又非理想塑性材料,而是介于二者之间的弹塑性材料。对于 低强度混凝士米说,塑性性能好 对高强度混凝士来说,其性 更接刘 弹性。当按 论计算纯扭构件的剪应力分布时,则低估了构件的抗扭开裂能力。此外,构件内除了作用有 主拉应力外,还有与主拉应力成正交方向的主压应力。在拉、压复合应力状态下,混凝土的 抗拉强度要低于单向受拉的抗拉强度,而且混凝土内的微裂缝、裂隙和局部缺陷又会引起应 力集中而降低构件的承载能力。 综上所述,矩形截面钢筋混凝土受扭构件的开裂扭矩,只能近似地采用理想塑性材料的 剪应力图形进行计算,同时通过试验来加以校正,乘以一个折减系数0.7。于是,开裂扭矩 的计算式为 T。=0.7Wf (5-2) 式中T。一一矩形截面纯扭构件的开裂扭矩: 厂a一一混凝土抗拉强度设计值: W,一一矩形截面的抗扭塑性抵抗矩。 5.1.2矩形截面纯扭构件的破坏特征 扭矩在构件中引起的主拉应力轨迹线与构件轴线成45°角,因此理论上讲在纯扭构件 中配置抗扭钢筋的最理想方案是沿45°方向布置螺旋形箍筋,使其与主拉应力方向一致, 以期取得较好的受力效果。然而,螺旋箍筋在受力上只能适应一个方向的扭矩,而在桥梁工 程中,由于活载作用,扭矩将不断变换方向,如果扭矩改变方向,则螺旋箍筋也必须相应地 改变方向,这在构适上是复杂的。因此 ,实际工 程中通常都采用由箍筋和纵 钢筋组成的 间骨架来承担扭矩,并尽可能地在保证必要的混凝土保护层厚度下,沿截面周边布置钢筋以 增强抗扭能力。 在抗扭钢筋骨架中,箍筋的作用是直接抵抗主拉应力,限制裂缝的发展:纵筋用来平衡 构件中的纵向分力,且在斜裂缝处纵筋可产生销栓作用,抵抗部分扭矩并可抑制斜裂缝的开 展。 抗扭钢筋的配置对矩形截面构件的抗扭能力有很大的影响。图5-6为不同抗扭配筋率的 受扭构件的T-0关系试验曲线。图5-6中P,为纵筋与箍筋的配筋率之和。由图5-6可知, 抗扭钢筋越少,裂缝出现引起的钢筋的应力突变就越大,水平段相对较长。当配筋很少时, 5-3
5-3 式中 Wt 称为矩形截面的抗扭塑性抵抗矩, Wt = ( h b) b 3 − 6 2 。 ) ) 图 5-5 矩形截面纯扭构件剪应力分布 a)弹性状态剪应力分布 b)塑性状态剪应力分布 但是混凝土既非弹性材料,又非理想塑性材料,而是介于二者之间的弹塑性材料。对于 低强度混凝土来说,塑性性能好一些;对高强度混凝土来说,其性能更接近于弹性。当按理 论计算纯扭构件的剪应力分布时,则低估了构件的抗扭开裂能力。此外,构件内除了作用有 主拉应力外,还有与主拉应力成正交方向的主压应力。在拉、压复合应力状态下,混凝土的 抗拉强度要低于单向受拉的抗拉强度,而且混凝土内的微裂缝、裂隙和局部缺陷又会引起应 力集中而降低构件的承载能力。 综上所述,矩形截面钢筋混凝土受扭构件的开裂扭矩,只能近似地采用理想塑性材料的 剪应力图形进行计算,同时通过试验来加以校正,乘以一个折减系数 0.7。于是,开裂扭矩 的计算式为 cr t td T = 0.7W f (5-2) 式中 Tcr ——矩形截面纯扭构件的开裂扭矩; td f ——混凝土抗拉强度设计值; Wt ——矩形截面的抗扭塑性抵抗矩。 5.1.2 矩形截面纯扭构件的破坏特征 扭矩在构件中引起的主拉应力轨迹线与构件轴线成 45°角,因此理论上讲在纯扭构件 中配置抗扭钢筋的最理想方案是沿 45°方向布置螺旋形箍筋,使其与主拉应力方向一致, 以期取得较好的受力效果。然而,螺旋箍筋在受力上只能适应一个方向的扭矩,而在桥梁工 程中,由于活载作用,扭矩将不断变换方向,如果扭矩改变方向,则螺旋箍筋也必须相应地 改变方向,这在构造上是复杂的。因此,实际工程中通常都采用由箍筋和纵向钢筋组成的空 间骨架来承担扭矩,并尽可能地在保证必要的混凝土保护层厚度下,沿截面周边布置钢筋以 增强抗扭能力。 在抗扭钢筋骨架中,箍筋的作用是直接抵抗主拉应力,限制裂缝的发展;纵筋用来平衡 构件中的纵向分力,且在斜裂缝处纵筋可产生销栓作用,抵抗部分扭矩并可抑制斜裂缝的开 展。 抗扭钢筋的配置对矩形截面构件的抗扭能力有很大的影响。图 5-6 为不同抗扭配筋率的 受扭构件的 T − 关系试验曲线。图 5-6 中 v 为纵筋与箍筋的配筋率之和。由图 5-6 可知, 抗扭钢筋越少,裂缝出现引起的钢筋的应力突变就越大,水平段相对较长。当配筋很少时
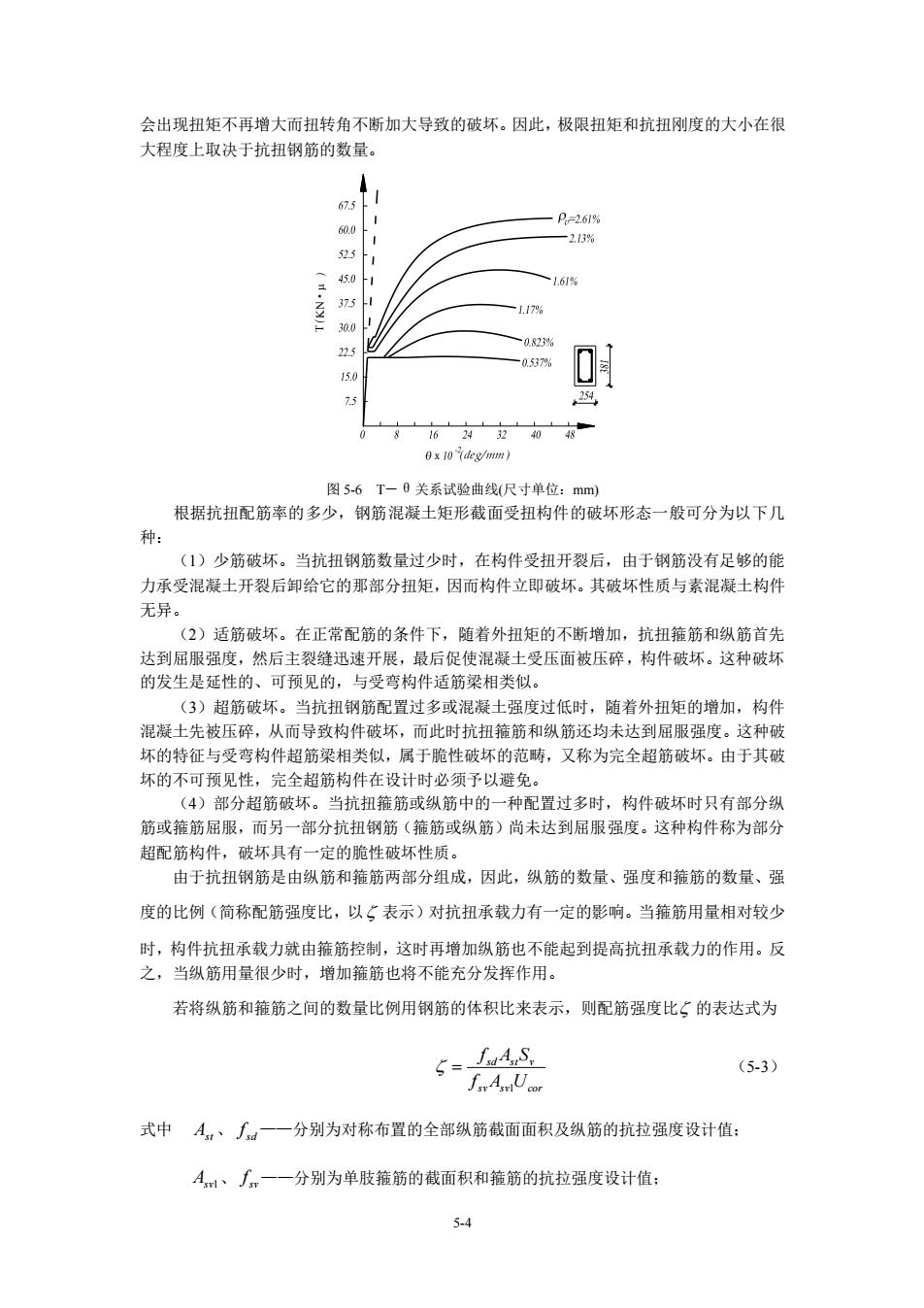
会出现扭矩不再增大而扭转角不断加大导致的破坏。因此,极限扭矩和抗扭刚度的大小在很 大程度上取决于抗扭钢筋的数量。 .0 52.5 450上 37.5 17 75 ,254 0 0x10deg/mn) 图5-6T一0关系试哈曲线尺寸单位:mm 根据抗扭配筋率的多少,钢筋混凝土矩形截面受扭构件的破坏形态一般可分为以下几 种: (1)少筋破坏。当抗扭钢筋数量过少时,在构件受扭开裂后,由于钢筋没有足够的能 力承受混凝土开裂后卸给它的那部分扭矩,因而构件立即破坏。其破坏性质与素混凝土构件 无异。 2)适筋破坏。在正常配筋的条件下,随着外扭矩的不断增加,抗扭箍筋和纵筋首先 达到屈服强度,然后主裂缝迅速开展,最后促使混凝土受压面被压碎,构件破坏。这种破坏 的发生是延性的、可预见的,与受弯构件适筋梁相类似。 (3)超筋破坏。当抗扭钢筋配置过多或混凝士强度过低时,随着外扭矩的增加,构件 混凝士先被压碎,从而导致构件破坏,而此时抗扭箍筋和纵筋还均未达到屈服强度。这种破 坏的特征与受弯构件超筋梁相类似,属于脆性破坏的范畴,又称为完全超筋破坏。由于其破 坏的不可预见性,完全超筋构件在设计时必须子以辟免。 (4)部分超筋破坏。当抗扭箍筋或纵筋中的一种配置过多时,构件破坏时只有部分纵 筋或箍筋屈服, 而另 部分抗扭钢筋(箍筋或纵筋)尚未达到屈服强度。这种构件称为部分 超配筋构件,破坏具有一定的脆性破坏性质。 由于抗扭钢筋是由纵筋和箍筋两部分组成,因此,纵筋的数量、强度和箍筋的数量、强 度的比例(简称配筋强度比,以5表示)对抗扭承载力有一定的影响。当箍筋用量相对较少 时,构件抗扭承载力就由箍筋控制,这时再增加纵筋也不能起到提高抗扭承载力的作用。反 之,当纵筋用量很少时,增加箍筋也将不能充分发挥作用。 若将纵筋和箍筋之间的数量比例用钢筋的体积比来表示,则配筋强度比5的表达式为 fAS. 5= (3) 式中A,、∫如一一分别为对称布置的全部纵筋截面面积及纵筋的抗拉强度设计值: A、∫,一一分别为单肢箍筋的截面积和箍筋的抗拉强度设计值: 5-4
5-4 会出现扭矩不再增大而扭转角不断加大导致的破坏。因此,极限扭矩和抗扭刚度的大小在很 大程度上取决于抗扭钢筋的数量。 x · 图 5-6 T-θ关系试验曲线(尺寸单位:mm) 根据抗扭配筋率的多少,钢筋混凝土矩形截面受扭构件的破坏形态一般可分为以下几 种: (1)少筋破坏。当抗扭钢筋数量过少时,在构件受扭开裂后,由于钢筋没有足够的能 力承受混凝土开裂后卸给它的那部分扭矩,因而构件立即破坏。其破坏性质与素混凝土构件 无异。 (2)适筋破坏。在正常配筋的条件下,随着外扭矩的不断增加,抗扭箍筋和纵筋首先 达到屈服强度,然后主裂缝迅速开展,最后促使混凝土受压面被压碎,构件破坏。这种破坏 的发生是延性的、可预见的,与受弯构件适筋梁相类似。 (3)超筋破坏。当抗扭钢筋配置过多或混凝土强度过低时,随着外扭矩的增加,构件 混凝土先被压碎,从而导致构件破坏,而此时抗扭箍筋和纵筋还均未达到屈服强度。这种破 坏的特征与受弯构件超筋梁相类似,属于脆性破坏的范畴,又称为完全超筋破坏。由于其破 坏的不可预见性,完全超筋构件在设计时必须予以避免。 (4)部分超筋破坏。当抗扭箍筋或纵筋中的一种配置过多时,构件破坏时只有部分纵 筋或箍筋屈服,而另一部分抗扭钢筋(箍筋或纵筋)尚未达到屈服强度。这种构件称为部分 超配筋构件,破坏具有一定的脆性破坏性质。 由于抗扭钢筋是由纵筋和箍筋两部分组成,因此,纵筋的数量、强度和箍筋的数量、强 度的比例(简称配筋强度比,以 表示)对抗扭承载力有一定的影响。当箍筋用量相对较少 时,构件抗扭承载力就由箍筋控制,这时再增加纵筋也不能起到提高抗扭承载力的作用。反 之,当纵筋用量很少时,增加箍筋也将不能充分发挥作用。 若将纵筋和箍筋之间的数量比例用钢筋的体积比来表示,则配筋强度比 的表达式为 sv sv cor sd st v f A U f A S 1 = (5-3) 式中 Ast 、 sd f ——分别为对称布置的全部纵筋截面面积及纵筋的抗拉强度设计值; Asv1、 sv f ——分别为单肢箍筋的截面积和箍筋的抗拉强度设计值;
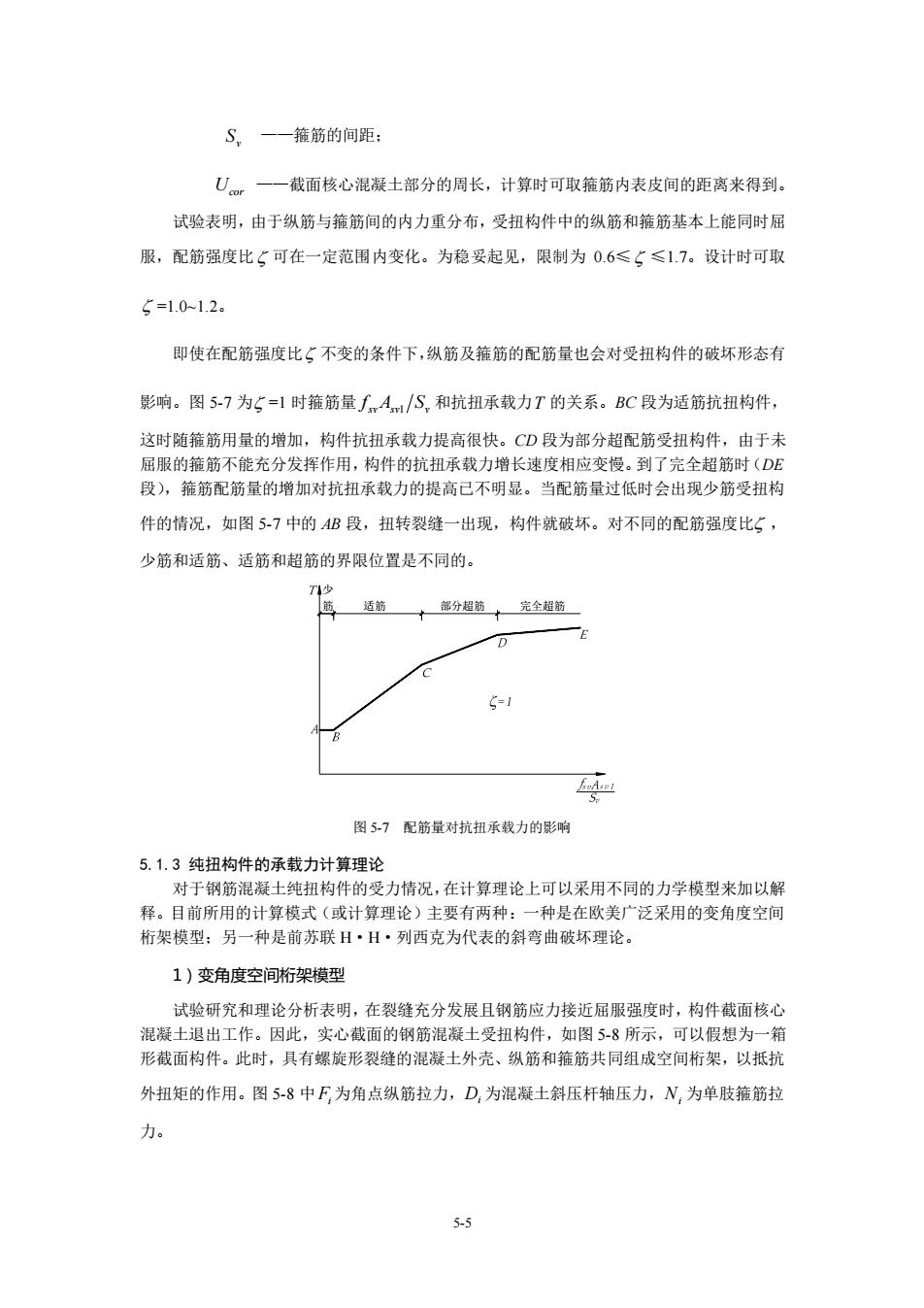
S.一一箍筋的间距 U。一一截面核心混凝士土部分的周长,计算时可取箍筋内表皮间的距离来得到。 试验表明,由于纵筋与箍筋间的内力重分布,受扭构件中的纵筋和箍筋基本上能同时屈 服,配筋强度比5可在一定范围内变化。为稳妥起见,限制为0.6≤(≤1.7。设计时可取 5=1.0-12。 即使在配筋强度比(不变的条件下,纵筋及箍筋的配筋量也会对受扭构件的破坏形态有 影响。图5-7为5=1时箍筋量,A/S,和抗扭承载力T的关系。BC段为适筋抗扭构件, 这时随箍筋用量的增加,构件抗扭承载力提高很快。CD段为部分超配筋受扭构件,由于未 屈服的推筋不能充分发挥作用,构件的抗扭承载力增长速度相应变慢。到了完全超筋时(D 段),箍筋配筋量的增加对抗扭承载力的提高已不明显。当配筋量过低时会出现少筋受扭构 件的情况,如图57中的AB段,扭转裂缝一出现,构件就破坏。对不同的配筋强度比5, 少筋和适筋、适筋和超筋的界限位置是不同的。 十部分超简十完全超 D 51 图5-7配筋量对抗扭承载力的影响 5.1.3纯扭构件的承载力计算理论 对于钢筋混凝土纯扭构件的受力情况,在计算理论上可以采用不同的力学模型来加以解 释。目前所用的计算模式(或计算理论)主要有两种:一种是在欧美广泛采用的变角度空间 桁架模型:另一种是前苏联H·H·列西克为代表的斜弯曲破坏理论。 1)变角度空间桁架模型 试验研究和理论分析表明,在裂缝充分发展且钢筋应力接近屈服强度时,构件截面核心 混凝土退出工作。因此,实心截面的钢筋混凝土受扭构件,如图5-8所示,可以假想为一箱 形截面构件。此时,具有螺旋形裂缝的混凝土外壳、纵筋和箍筋共同组成空间桁架,以抵抗 外扭矩的作用。图5-8中F为角点纵筋拉力,D,为混凝土斜压杆轴压力,N,为单肢箍筋拉 力
5-5 v S ——箍筋的间距; Ucor ——截面核心混凝土部分的周长,计算时可取箍筋内表皮间的距离来得到。 试验表明,由于纵筋与箍筋间的内力重分布,受扭构件中的纵筋和箍筋基本上能同时屈 服,配筋强度比 可在一定范围内变化。为稳妥起见,限制为 0.6≤ ≤1.7。设计时可取 =1.0~1.2。 即使在配筋强度比 不变的条件下,纵筋及箍筋的配筋量也会对受扭构件的破坏形态有 影响。图 5-7 为 =1 时箍筋量 svAsv Sv f 1 和抗扭承载力 T 的关系。BC 段为适筋抗扭构件, 这时随箍筋用量的增加,构件抗扭承载力提高很快。CD 段为部分超配筋受扭构件,由于未 屈服的箍筋不能充分发挥作用,构件的抗扭承载力增长速度相应变慢。到了完全超筋时(DE 段),箍筋配筋量的增加对抗扭承载力的提高已不明显。当配筋量过低时会出现少筋受扭构 件的情况,如图 5-7 中的 AB 段,扭转裂缝一出现,构件就破坏。对不同的配筋强度比 , 少筋和适筋、适筋和超筋的界限位置是不同的。 少 筋 适筋 部分超筋 完全超筋 图 5-7 配筋量对抗扭承载力的影响 5.1.3 纯扭构件的承载力计算理论 对于钢筋混凝土纯扭构件的受力情况,在计算理论上可以采用不同的力学模型来加以解 释。目前所用的计算模式(或计算理论)主要有两种:一种是在欧美广泛采用的变角度空间 桁架模型;另一种是前苏联 H·H·列西克为代表的斜弯曲破坏理论。 1)变角度空间桁架模型 试验研究和理论分析表明,在裂缝充分发展且钢筋应力接近屈服强度时,构件截面核心 混凝土退出工作。因此,实心截面的钢筋混凝土受扭构件,如图 5-8 所示,可以假想为一箱 形截面构件。此时,具有螺旋形裂缝的混凝土外壳、纵筋和箍筋共同组成空间桁架,以抵抗 外扭矩的作用。图 5-8 中 Fi 为角点纵筋拉力, Di 为混凝土斜压杆轴压力, Ni 为单肢箍筋拉 力

图58变角度空间桁架模型 a计算模型示意图b)环向剪力流©)内力平衡图 变角度空间桁架模型的基本假定有: (1)混凝土只承受压力,具有螺旋形裂缝的混凝土外壳组成桁架的斜压杆,其倾角为α: (2)纵筋和箍筋只承受拉力,分别构成桁架的弦杆和煦杆: (3)忽略核心混凝土的抗扭作用和钢筋的销栓作用 在上述假定中,忽略核心混凝士的抗扭作用的假定更为重要。这样,实心截面构件可以 看作为一箱形截面构件或一薄壁管构件,从而在受扭承载力计算中,可应用薄壁管理论。 由薄壁管理论,在扭矩T作用下,沿箱形截面侧壁中将产生大小相同的环向剪力流q, 如图5-8b)所示,且由图可得到 q=1=2 (5-4) 式中A一一剪力流路线所围成的面积,此处取为构件核心截面积即箍筋内表面所围成的 面积: T 一扭矩产生的剪应力: 箱形碱面侧壁厚度。 图5-8c)所示为作用于侧壁的剪力流g引起的桁架各杆件的内力图,其中α为斜压杆的 倾角,为单肢箍筋拉力总和,F为纵筋拉力总和,D为混凝土斜压杆轴压力之和。由图 示力学平衡条件可得到 N=F.tand (5-5) 在极限状态下: N=24mh cota24bo cota Am2(+)cota 6
5-6 ) ) ) 图 5-8 变角度空间桁架模型 a)计算模型示意图 b)环向剪力流 c)内力平衡图 变角度空间桁架模型的基本假定有: (1)混凝土只承受压力,具有螺旋形裂缝的混凝土外壳组成桁架的斜压杆,其倾角为 ; (2)纵筋和箍筋只承受拉力,分别构成桁架的弦杆和腹杆; (3)忽略核心混凝土的抗扭作用和钢筋的销栓作用。 在上述假定中,忽略核心混凝土的抗扭作用的假定更为重要。这样,实心截面构件可以 看作为一箱形截面构件或一薄壁管构件,从而在受扭承载力计算中,可应用薄壁管理论。 由薄壁管理论,在扭矩 Tu 作用下,沿箱形截面侧壁中将产生大小相同的环向剪力流 q , 如图 5-8b)所示,且由图可得到 2 u cor T q t A = = (5-4) 式中 Acor ——剪力流路线所围成的面积,此处取为构件核心截面积,即箍筋内表面所围成的 面积; ——扭矩产生的剪应力; t ——箱形截面侧壁厚度。 图 5-8c)所示为作用于侧壁的剪力流 q 引起的桁架各杆件的内力图,其中 为斜压杆的 倾角, N 为单肢箍筋拉力总和, F 为纵筋拉力总和,D为混凝土斜压杆轴压力之和。由图 示力学平衡条件可得到 N F= tan (5-5) 在极限状态下: ( ) 1 1 1 cot cot 2 2 2 cot sv sv cor sv sv cor v v sv sv cor cor v A f h A f b N S S A f h b S = + + =
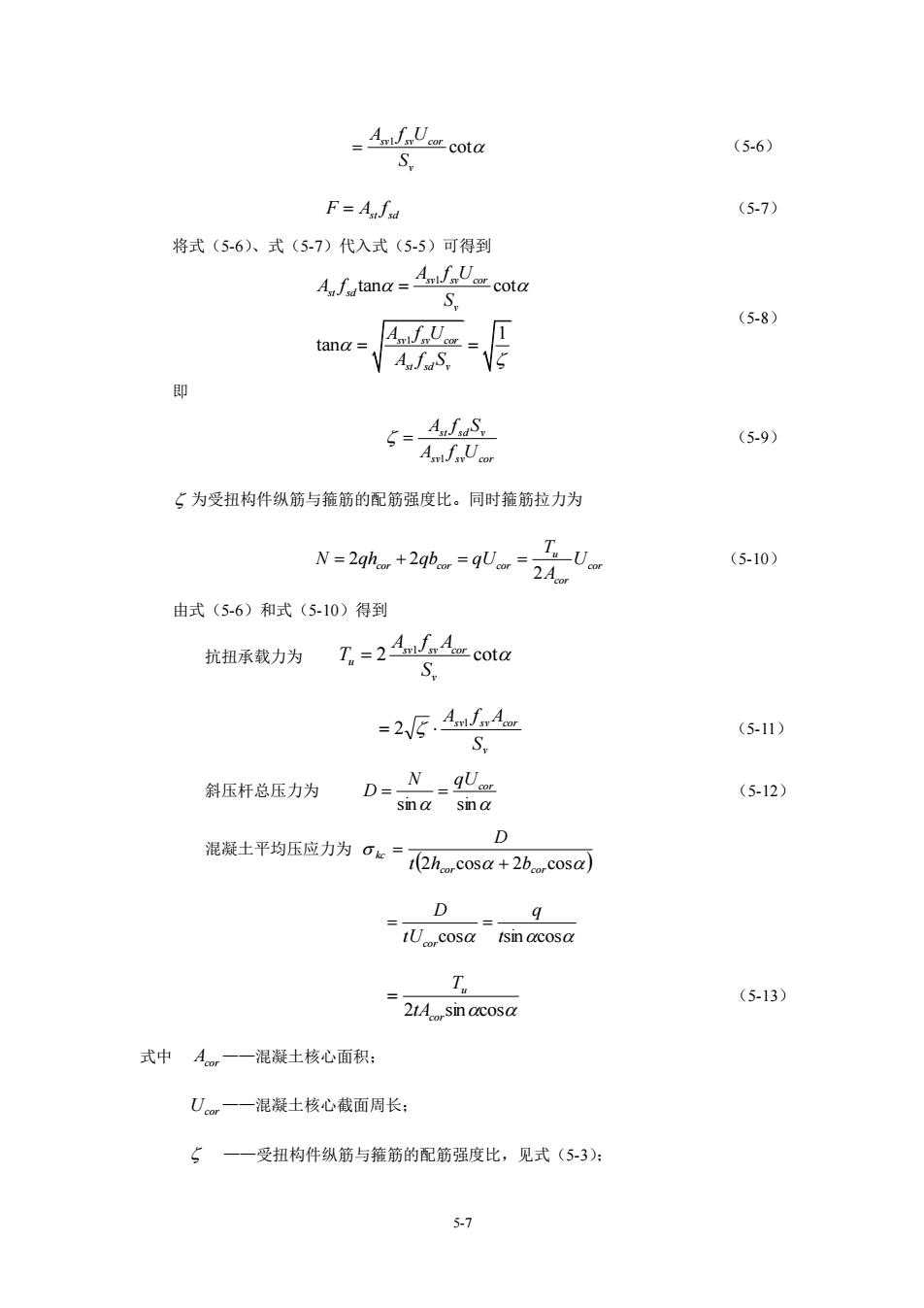
Amf.U cota (5-6) F=A∫a 5 将式(5-6)、式(5-7)代入式(5-5)可得到 A/aamw=4a人L_cota 恶 50 AmfUcor 二为受扭构件纵筋与箍筋的配筋强度比。同时箍筋拉力为 T N=2g+2g0.=g02元 (5.10) 由式(5-6)和式(5-10)得到 抗扭承载力为T.=24m人4cota S -2VE.AA s, 斜压杆总压力为 D= 混凝士平均压应力为0s-亿hc0sa+2hc0sa D cos sin acosa T 21Asin ccosa 式中A一一混凝土核心面积: U一一混凝士核心截面周长 5一—受扭构件纵筋与箍筋的配筋强度比,见式(5-3): 5-7
5-7 1 cot sv sv cor v A f U S = (5-6) st sd F = A f (5-7) 将式(5-6)、式(5-7)代入式(5-5)可得到 1 1 tan cot 1 tan sv sv cor st sd v sv sv cor st sd v A f U A f S A f U A f S = = = (5-8) 即 sv sv cor st sd v A f U A f S 1 = (5-9) 为受扭构件纵筋与箍筋的配筋强度比。同时箍筋拉力为 2 2 2 u cor cor cor cor cor T N qh qb qU U A = + = = (5-10) 由式(5-6)和式(5-10)得到 抗扭承载力为 1 2 cot sv sv cor u v A f A T S = v sv sv cor S A 1 f A = 2 (5-11) 斜压杆总压力为 sin sin N qUcor D = = (5-12) 混凝土平均压应力为 ( ) 2 cos 2 cos cor cor kc t h b D + = cos tsincos q tU D cor = = 2 corsincos u tA T = (5-13) 式中 Acor ——混凝土核心面积; Ucor ——混凝土核心截面周长; ——受扭构件纵筋与箍筋的配筋强度比,见式(5-3);

A,—纯扭计算中沿截面周边对称配置的全部纵向钢筋截面积: A一一箍筋单肢面积: S,一抗扭箍筋间距: ∫。一抗扭纵筋抗拉强度设计值: ∫,一一抗扭筘筋抗拉强度设计值。 由式(5-11)可以看出,构件的扭矩承载力T,主要与钢筋骨架尺寸、箍筋用量及其强度, 以及表征纵筋与箍筋的相对用量的参数5有关。按照变角度空间桁架模型,不仅有如式 (5-9)的物理意义,而且有如公式(58)所示表征斜压杆倾角α的大小,因而在计算模 型中还具有一定的几何意义。 式(51)为低配筋受扭构件扭矩承载力的计算公式。为了保证钢筋应力达到屈服强度 前不发生混凝士压坏,即避免出现超筋构件的脆性破坏,必须限制按公式(5-13)计算得到 的斜压杆平均应力σ的大小。 2)斜弯曲破坏理论(亦称扭曲破坏面极限平衡理论) 斜弯曲破坏理论是以实验为基础的。对于纯扭的钢筋混凝土构件,在扭矩作用下,构件 总是在己经形成螺旋形裂缝的某一最薄弱的空间曲面发生破坏。如图5-9所示,AB、BC、 CD、为三段连续的斜向破坏裂缝,其与构件纵轴线方向的夹角为α。AD段为倾斜压区。斜 弯曲破坏理论乃是截取实际的破坏面作为隔离体,从而直接导出与纵筋、箍筋用量有关的抗 扭承载力计算公式的。 斜弯曲计算理论的基本假定为: (1)假定通过扭曲裂面的纵向钢筋、箍筋在构件破坏时均已达到其屈服强度: (2)受压区高度近似地取为两倍的保护层厚度,即受压区重心正位于箍筋处。假定受 压区的合力近似地作用于受压区的形心: (3)混凝土的抗扭能力忽略不计,扭矩全部由抗扭纵筋和箍筋承担: (4)假定抗扭纵筋沿构件核心周边对称、均匀布置,抗扭箍筋沿构件轴线方向等距离 布置,且均错固可靠。 根据以上基本假定,令通过受压区形心而平行于构件纵向中心轴x的轴为H轴,由对 该轴的内外扭矩的静力平衡条件可得到 58
5-8 Ast ——纯扭计算中沿截面周边对称配置的全部纵向钢筋截面积; Asv1——箍筋单肢面积; v S ——抗扭箍筋间距; sd f ——抗扭纵筋抗拉强度设计值; sv f ——抗扭箍筋抗拉强度设计值。 由式(5-11)可以看出,构件的扭矩承载力 Tu 主要与钢筋骨架尺寸、箍筋用量及其强度, 以及表征纵筋与箍筋的相对用量的参数 有关。按照变角度空间桁架模型, 不仅有如式 (5-9)的物理意义,而且有如公式(5- 8 )所示表征斜压杆倾角 的大小,因而在计算模 型中还具有一定的几何意义。 式(5-11)为低配筋受扭构件扭矩承载力的计算公式。为了保证钢筋应力达到屈服强度 前不发生混凝土压坏,即避免出现超筋构件的脆性破坏,必须限制按公式(5-13)计算得到 的斜压杆平均应力 kc 的大小。 2)斜弯曲破坏理论(亦称扭曲破坏面极限平衡理论) 斜弯曲破坏理论是以实验为基础的。对于纯扭的钢筋混凝土构件,在扭矩作用下,构件 总是在已经形成螺旋形裂缝的某一最薄弱的空间曲面发生破坏。如图 5-9 所示,AB、BC、 CD、为三段连续的斜向破坏裂缝,其与构件纵轴线方向的夹角为 。AD 段为倾斜压区。斜 弯曲破坏理论乃是截取实际的破坏面作为隔离体,从而直接导出与纵筋、箍筋用量有关的抗 扭承载力计算公式的。 斜弯曲计算理论的基本假定为: (1)假定通过扭曲裂面的纵向钢筋、箍筋在构件破坏时均已达到其屈服强度; (2)受压区高度近似地取为两倍的保护层厚度,即受压区重心正位于箍筋处。假定受 压区的合力近似地作用于受压区的形心; (3)混凝土的抗扭能力忽略不计,扭矩全部由抗扭纵筋和箍筋承担; (4)假定抗扭纵筋沿构件核心周边对称、均匀布置,抗扭箍筋沿构件轴线方向等距离 布置,且均锚固可靠。 根据以上基本假定,令通过受压区形心而平行于构件纵向中心轴 x 的轴为 I-I 轴,由对 该轴的内外扭矩的静力平衡条件可得到

图5-9斜弯曲理论计算示意图 (5-14) 再令通过受压区形心而平行于y轴的轴为Ⅱ轴,则由对该轴的内力矩为零的条件, 可得到 dyb.cota(h_coia+b.cota)-h 解之可得到 tana=, Af Uor (5-15) 将式(5-15)代入式(5-14),可得到 7=2F44 (5-16) S 由此可知,在上述近似假定的条件,按斜弯曲理论得出的扭矩承载力计算式(5-16)与 按变角度空间桁架理论所得的计算式(511)完全相同。 5.1.4《公路桥规》对矩形截面纯扭构件的承载力计算 由空间桁架计算模型或斜弯理论导出的受扭构件承载力计算公式充分反映了抗扭钢筋 的作用。但试验表明在低配筋时偏于保守,在高配筋时,由于纵向钢筋和箍筋不能同时屈服, 计算值又偏高。试验观测还表明,受扭构件开裂以后,由于钢筋对混凝土的约束,裂缝开展 受到 一定的限市 斜裂缝间混凝土的骨料咬合力还较大 使得混 凝土仍具有 定的 同时,受扭裂缝往往是许多分布在四个侧面上相互平行、断断续续、前后交错的斜裂缝,这 些斜裂缝只从表面向内延伸到一定的深度而不会贯穿整个截面,最终也不完全形成连续的、 通长的螺旋形裂缝,混凝土本身没有被分割成可动机构,在开裂后仍然能承担一部分扭矩。 因此,在外扭矩作用下,钢筋混凝土受扭构件实际上是由钢筋(纵筋和箍筋)和混凝土共同 提供构件的抗扭承载力T。,即由钢筋承担的扭矩T,和混凝土承担的扭矩T组成: T.=I.+r. 基于变角度空间桁架的计算模型,并通过受扭构件的室内试验且使总的抗扭能力取试验
5-9 受压区 Ι Ι ΙΙ ΙΙ 图 5-9 斜弯曲理论计算示意图 1 1 1 cot cot 2 cot sv sv sv sv sv sv u cor cor cor cor cor cor v v v A f A f A f T h b b h h b S S S = + = (5-14) 再令通过受压区形心而平行于 y 轴的轴为 II-II 轴,则由对该轴的内力矩为零的条件, 可得到 ( ) 1 1 cot cot cot 2 sv sv cor cor cor st sd cor v A f b h b A f b S + = 解之可得到 1 1 tan sv sv cor st sd v A f U A f S = = (5-15) 将式(5-15)代入式(5-14),可得到 1 2 sv sv cor u v A f A T S = (5-16) 由此可知,在上述近似假定的条件,按斜弯曲理论得出的扭矩承载力计算式(5-16)与 按变角度空间桁架理论所得的计算式(5-11)完全相同。 5.1.4 《公路桥规》对矩形截面纯扭构件的承载力计算 由空间桁架计算模型或斜弯理论导出的受扭构件承载力计算公式充分反映了抗扭钢筋 的作用。但试验表明在低配筋时偏于保守,在高配筋时,由于纵向钢筋和箍筋不能同时屈服, 计算值又偏高。试验观测还表明,受扭构件开裂以后,由于钢筋对混凝土的约束,裂缝开展 受到一定的限制,斜裂缝间混凝土的骨料咬合力还较大,使得混凝土仍具有一定的咬合力。 同时,受扭裂缝往往是许多分布在四个侧面上相互平行、断断续续、前后交错的斜裂缝,这 些斜裂缝只从表面向内延伸到一定的深度而不会贯穿整个截面,最终也不完全形成连续的、 通长的螺旋形裂缝,混凝土本身没有被分割成可动机构,在开裂后仍然能承担一部分扭矩。 因此,在外扭矩作用下,钢筋混凝土受扭构件实际上是由钢筋(纵筋和箍筋)和混凝土共同 提供构件的抗扭承载力 Tu ,即由钢筋承担的扭矩 TS 和混凝土承担的扭矩 Tc 组成: Tu = Tc + Ts 基于变角度空间桁架的计算模型,并通过受扭构件的室内试验且使总的抗扭能力取试验

数据的偏下值,得到《公路桥规》中采用的矩形截面构件抗扭承载力计算公式并应满足: ≤7。=035/m+1.2544 (5-17) S 式中T.一一扭矩组合设计值(N·mm): T一一抗扭承载力: 用一凭形黄面受扣塑性抵抗矩(mm所一名公G助-小: A一一箍筋单肢截面面积(mm2) Aor一一箍筋内表面所围成的混凝土核心面积,Aor=baho,此处b和h,分别 为核心面积的短边和长边边长。 S,一一抗扭箍筋间距(mm): ∫a一混凝土抽心抗拉强度设计值(MPa)为 ∫,一一抗扭箍筋抗拉强度设计值(MPa)。 5为纯扭构件纵向钢筋与箍筋的配筋强度比,按公式(5-3)计算:对钢筋混凝士构件,《公 路桥规》规定5值应符合0.6≤5≤1.7,当5>1.7时,取5=1.7。 应用式(5-17)计算构件的抗扭承载力时,必须满足《公路桥规》提出的限制条件。 1)抗扭配筋的上限值 当抗扭钢筋配量过多时,受扭构件可能在抗扭钢筋屈服以前便由于混凝土被压碎而破 坏。这时,即使进一步增加钢筋,构件所能承担的破坏扭矩几乎不再增长,也就是说,其破 坏扭矩取决于混凝土的强度和截面尺寸。因此,《公路桥规》规定钢筋混凝土矩形截面纯扭 构件的截面尺寸应符合式(5-18)要求: YL≤0.51x103VTa (kN/mm) (5.18) 式中工,一一扭矩组合设计值(W,m): 用,一一矩形截面受扭塑性抵抗矩(mm): 厂一一混凝土立方体抗压强度标准值(MPa)。 2)抗扭配筋的下限值 5-10
5-10 数据的偏下值,得到《公路桥规》中采用的矩形截面构件抗扭承载力计算公式并应满足: 0Td ≤ Tu = v sv sv cor td t S f A A f W 1 0.35 +1.2 (5-17) 式中 Td ——扭矩组合设计值( N mm ); Tu ——抗扭承载力; Wt ——矩形截面受扭塑性抵抗矩( 3 mm ), (3 ) 6 2 h b b Wt = − ; Asv1——箍筋单肢截面面积( 2 mm ); Acor ——箍筋内表面所围成的混凝土核心面积, Acor = bcorhcor ,此处 bcor和hcor 分别 为核心面积的短边和长边边长。 v S ——抗扭箍筋间距( mm ); td f ——混凝土轴心抗拉强度设计值( MPa ); sv f ——抗扭箍筋抗拉强度设计值( MPa )。 为纯扭构件纵向钢筋与箍筋的配筋强度比,按公式(5-3)计算;对钢筋混凝土构件,《公 路桥规》规定 值应符合 0.6≤ ≤1.7,当 >1.7 时,取 =1.7。 应用式(5-17)计算构件的抗扭承载力时,必须满足《公路桥规》提出的限制条件。 1)抗扭配筋的上限值 当抗扭钢筋配量过多时,受扭构件可能在抗扭钢筋屈服以前便由于混凝土被压碎而破 坏。这时,即使进一步增加钢筋,构件所能承担的破坏扭矩几乎不再增长,也就是说,其破 坏扭矩取决于混凝土的强度和截面尺寸。因此,《公路桥规》规定钢筋混凝土矩形截面纯扭 构件的截面尺寸应符合式(5-18)要求: 0 3 , 0.51 10 d cu k t T f W − 2 ( ) kN mm (5-18) 式中 Td ——扭矩组合设计值( kN mm ); Wt ——矩形截面受扭塑性抵抗矩( 3 mm ); cu k, f ——混凝土立方体抗压强度标准值( MPa )。 2)抗扭配筋的下限值