
第一篇钢筋混凝土结构 第1章钢筋混凝土结构的基本概念及 材料的物理力学性能 1.1钢筋混凝土结构的基本概念 钢筋混凝士结构是由配置受力的普通钢筋或钢筋骨架的混凝士制成的结构。 混凝土是一种人造石料,其抗压能力很高,而抗拉能力很弱。采用素混凝土制成的构件 (指无筋或不配置受力钢筋的混凝土构件),例如素混凝土梁,当它承受竖向荷载作用时图 1-1)],在梁的垂直截面(正截面)上受到弯矩作用,截面中和轴以上受压,以下受拉 当荷载达到某 数值F时,梁截面的受拉边缘 土的拉应变达到极限拉应变,即出现雪 向弯曲裂缝,这时,裂缝处截面的受拉区混凝土退出工作,该截面处受压高度减小,即使荷 载不增加,竖向弯曲裂缝也会急速向上发展,导致梁骤然断裂[图11b)]。这种破坏是很突 然的。也就是说,当荷载达到F。的瞬间,梁立即发生破坏。F。为素混凝士梁受拉区出现裂 缝的荷我,一般称为素混凝土梁的抗寥荷载,也是素混凝土梁的破坏荷载。由此可见,素混 凝土梁的承载能力是由混凝土的抗拉强度控制的,而受压混凝土的抗压强度远未被充分利 用。在制造混凝土梁时,徜若在梁的受拉区配置适量的纵向受力钢筋,就构成钢筋混凝土梁 试验表明,和素混凝士梁有相同截面尺寸的钢筋混凝土梁承受竖向荷载作用时,荷载略大于 F。时的受拉区混凝土仍会出现裂缝。在出现裂缝的藏面处,受拉区混凝土虽退出工作,但 配置在受拉区的钢筋将可承担几乎全部的拉力。这时,钢筋混凝土梁不会像素混凝土梁那样 立即裂断,而能继续承受荷载作用图11c),直至受拉钢筋的应力达到屈服强度,继而截 面受压区的混凝士也被压碎,梁才破坏。因此,混凝士的抗压强度和钢筋的抗拉强度都能得 到充分的利用,钢筋混凝土梁的承载能力可较素混凝土梁提高很多。 图 受拉区 中性 图1一1素混凝土梁和枫筋湿凝士梁 )受竖向力作用的混凝土梁b)素混凝土梁的新裂c)钢筋混凝土梁的开裂 混凝土的抗压强度高,常用于受压构件。若在构件中配置钢筋来构成钢筋混凝土受压构 件,试验表明,和素混凝土受压构件截面尺寸及长细比相同的钢筋混凝士受压构件,不仅承 载能力大为提高,而且受力性能得到改善(图12)。在这种情况下,钢筋的作用主要是协 1-1
1-1 第一篇 钢筋混凝土结构 第 1 章 钢筋混凝土结构的基本概念及 材料的物理力学性能 1.1 钢筋混凝土结构的基本概念 钢筋混凝土结构是由配置受力的普通钢筋或钢筋骨架的混凝土制成的结构。 混凝土是一种人造石料,其抗压能力很高,而抗拉能力很弱。采用素混凝土制成的构件 (指无筋或不配置受力钢筋的混凝土构件),例如素混凝土梁,当它承受竖向荷载作用时[图 1-1a)],在梁的垂直截面(正截面)上受到弯矩作用,截面中和轴以上受压,以下受拉。 当荷载达到某一数值 Fc 时,梁截面的受拉边缘混凝土的拉应变达到极限拉应变,即出现竖 向弯曲裂缝,这时,裂缝处截面的受拉区混凝土退出工作,该截面处受压高度减小,即使荷 载不增加,竖向弯曲裂缝也会急速向上发展,导致梁骤然断裂[图 1-1b)]。这种破坏是很突 然的。也就是说,当荷载达到 Fc 的瞬间,梁立即发生破坏。Fc 为素混凝土梁受拉区出现裂 缝的荷载,一般称为素混凝土梁的抗裂荷载,也是素混凝土梁的破坏荷载。由此可见,素混 凝土梁的承载能力是由混凝土的抗拉强度控制的,而受压混凝土的抗压强度远未被充分利 用。在制造混凝土梁时,倘若在梁的受拉区配置适量的纵向受力钢筋,就构成钢筋混凝土梁。 试验表明,和素混凝土梁有相同截面尺寸的钢筋混凝土梁承受竖向荷载作用时,荷载略大于 Fc 时的受拉区混凝土仍会出现裂缝。在出现裂缝的截面处,受拉区混凝土虽退出工作,但 配置在受拉区的钢筋将可承担几乎全部的拉力。这时,钢筋混凝土梁不会像素混凝土梁那样 立即裂断,而能继续承受荷载作用[图 1-1c)],直至受拉钢筋的应力达到屈服强度,继而截 面受压区的混凝土也被压碎,梁才破坏。因此,混凝土的抗压强度和钢筋的抗拉强度都能得 到充分的利用,钢筋混凝土梁的承载能力可较素混凝土梁提高很多。 1 1 受拉区 1 1= 1 1 裂缝 ) ) ) 受拉区 中性轴 中性轴 图 1-1 素混凝土梁和钢筋混凝土梁 a)受竖向力作用的混凝土梁 b)素混凝土梁的断裂 c)钢筋混凝土梁的开裂 混凝土的抗压强度高,常用于受压构件。若在构件中配置钢筋来构成钢筋混凝土受压构 件,试验表明,和素混凝土受压构件截面尺寸及长细比相同的钢筋混凝土受压构件,不仅承 载能力大为提高,而且受力性能得到改善(图 1-2)。在这种情况下,钢筋的作用主要是协
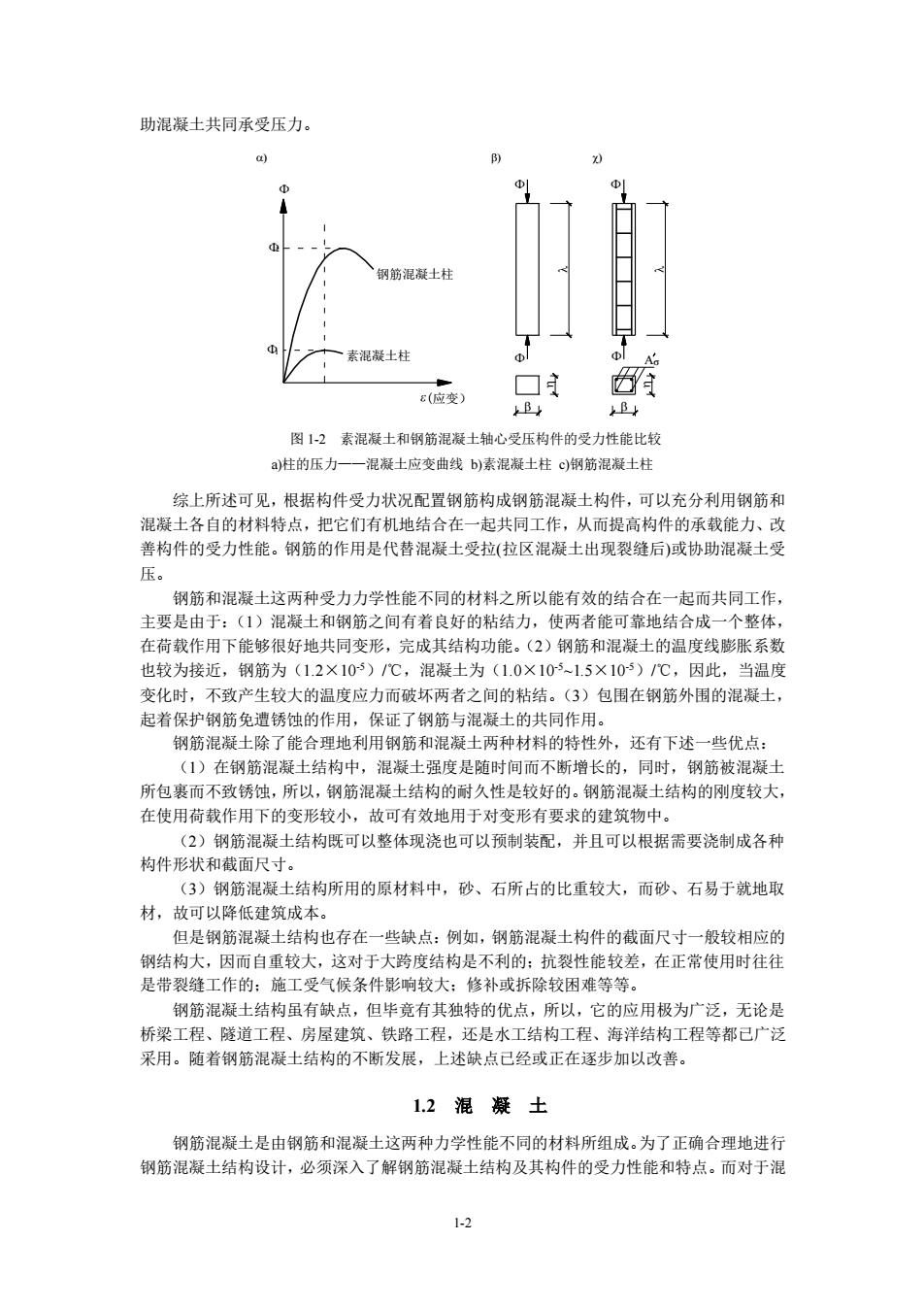
助混凝土共同承受压力。 素混凝土柱 应变) B 图12素混凝土和钢筋混凝士轴心受压构件的受力性能比较 a柱的压力一一混凝土应变曲线b)索混凝士柱c)钢筋混凝士柱 综上所述可见,根据构件受力状况配置钢筋构成钢筋混凝土构件,可以充分利用钢筋和 混凝土各自的材料特点,把它们有机地结合在一起共同工作,从而提高构件的承载能力、改 善构件的受力性能。钢筋的作用是代替混凝土受拉(拉区混凝士出现裂缝后)或协助混凝土受 压。 钢筋和混凝土这两种受力力学性能不同的材料之所以能有效的结合在一起而共同工作, 主要是由于:(1)混凝土和钢筋之间有者良好的粘结力,使两者能可靠地结合成一个整体, 在荷载作用下能够很好地共同变形,完成其结构功能。(2)钢筋和混凝土的温度线膨胀系数 也较为接近,钢筋为(1.2×10)/℃,混凝土为(1.0×1051.5×10)℃,因此,当温度 变化时,不致产生较大的温度应力而破坏两者之间的粘结。(3)包围在钢筋外围的混凝土, 起着保护钢筋免遭锈蚀的作用,保证了钢筋与混凝士的共同作用。 钢筋混凝土除了能合理地利用钢筋和混凝士两种材料的特性外,还有下述一些优点: (1)在钢筋混凝士结构中,混凝土强度是随时间而不晰增长的,同时,钢筋被混凝士 所包裹而不致锈蚀,所以,钢筋混凝土结构的耐久性是较好的。钢筋混凝土结构的刚度较大, 在使用荷载作用下的变形较小,故可有效地用于对变形有要求的建筑物中。 (2)钢筋混凝土结构既可以整体现浇也可以预制装配,并且可以根据需要浇制成各种 构件形状和截面尺寸。 (3)钢筋混凝土结构所用的原材料中,砂、石所占的比重较大,而砂、石易于就地取 材,故可以降低律筑成本 但是钢筋混凝士结构也存在一些缺点:例如,钢筋混凝土构件的截面尺寸一般较相应的 钢结构大,因而自重较大 这对于大跨度结构是 不利的:抗裂性能较差,在正常使用时往往 是带裂缝工作的:施工受气候条件影响较大:修补或拆除较困难等等。 钢筋混凝土结构虽有缺点,但毕竟有其独特的优点,所以,它的应用极为广泛,无论是 桥梁工程、隧道工程、房屋建筑、铁路工程,还是水工结构工程、海洋结构工程等都已广泛 采用。随着钢筋混凝土结构的不发展,上述缺点已经或正在逐步加以改善。 1.2混凝土 钢筋混凝土是由钢筋和混凝土这两种力学性能不同的材料所组成。为了正确合理地进行 钢筋混凝土结构设计,必须深入了解钢筋混凝土结构及其构件的受力性能和特点。而对于混 人
1-2 助混凝土共同承受压力。 ) ) ) 钢筋混凝土柱 素混凝土柱 (应变) 图 1-2 素混凝土和钢筋混凝土轴心受压构件的受力性能比较 a)柱的压力——混凝土应变曲线 b)素混凝土柱 c)钢筋混凝土柱 综上所述可见,根据构件受力状况配置钢筋构成钢筋混凝土构件,可以充分利用钢筋和 混凝土各自的材料特点,把它们有机地结合在一起共同工作,从而提高构件的承载能力、改 善构件的受力性能。钢筋的作用是代替混凝土受拉(拉区混凝土出现裂缝后)或协助混凝土受 压。 钢筋和混凝土这两种受力力学性能不同的材料之所以能有效的结合在一起而共同工作, 主要是由于:(1)混凝土和钢筋之间有着良好的粘结力,使两者能可靠地结合成一个整体, 在荷载作用下能够很好地共同变形,完成其结构功能。(2)钢筋和混凝土的温度线膨胀系数 也较为接近,钢筋为(1.2×10-5)/℃,混凝土为(1.0×10-5~1.5×10-5)/℃,因此,当温度 变化时,不致产生较大的温度应力而破坏两者之间的粘结。(3)包围在钢筋外围的混凝土, 起着保护钢筋免遭锈蚀的作用,保证了钢筋与混凝土的共同作用。 钢筋混凝土除了能合理地利用钢筋和混凝土两种材料的特性外,还有下述一些优点: (1)在钢筋混凝土结构中,混凝土强度是随时间而不断增长的,同时,钢筋被混凝土 所包裹而不致锈蚀,所以,钢筋混凝土结构的耐久性是较好的。钢筋混凝土结构的刚度较大, 在使用荷载作用下的变形较小,故可有效地用于对变形有要求的建筑物中。 (2)钢筋混凝土结构既可以整体现浇也可以预制装配,并且可以根据需要浇制成各种 构件形状和截面尺寸。 (3)钢筋混凝土结构所用的原材料中,砂、石所占的比重较大,而砂、石易于就地取 材,故可以降低建筑成本。 但是钢筋混凝土结构也存在一些缺点:例如,钢筋混凝土构件的截面尺寸一般较相应的 钢结构大,因而自重较大,这对于大跨度结构是不利的;抗裂性能较差,在正常使用时往往 是带裂缝工作的;施工受气候条件影响较大;修补或拆除较困难等等。 钢筋混凝土结构虽有缺点,但毕竟有其独特的优点,所以,它的应用极为广泛,无论是 桥梁工程、隧道工程、房屋建筑、铁路工程,还是水工结构工程、海洋结构工程等都已广泛 采用。随着钢筋混凝土结构的不断发展,上述缺点已经或正在逐步加以改善。 1.2 混 凝 土 钢筋混凝土是由钢筋和混凝土这两种力学性能不同的材料所组成。为了正确合理地进行 钢筋混凝土结构设计,必须深入了解钢筋混凝土结构及其构件的受力性能和特点。而对于混

凝土和钢筋材料的物理力学性能(强度和变形的变化规律)的了解,则是掌握钢筋混凝土结 构的构件性能、分析和设计的基础。 1.2.1混凝土的强度 1)混凝土立方体抗压强度 混凝土的立方体抗压强度是规定的标准试件和标准试验方法得到的混凝土强度基本代 表值。我国取用的标准试件为边长相等的混凝土立方体,这种试件的制作和试验均比较简便 而且离散性较小。 我国国家标准《普通混凝土力学性能试验方法标准》(GB/T50081-2002)规定以每边边 长为150mm的立方体为标准试件,在(20士2)℃的温度和相对湿度在95%以上的潮湿空 气中养护28天 依照标准制作 方法和试验方法测得的抗压强度值(以Nmm为单位)作为 混凝土的立方体抗压强度,用符号表示。按这样的规定,就可以排除不同制作方法、养 护环境等因素对混凝士立方体强度的影响。 混凝土立方体抗压强度与试验方法有着密切的关系。在通常情况下,试件的上下表面与 试验机承压板之间将产生阻止试件向外自由变形的摩阻力,阻滞了裂缝的发展[图1-3)], 从而提高了试块的抗压强度。破坏时,远离承压板的试件中部混凝士所受的约束最少,混凝 土也剥落得最多,形成两个对顶叠置的截头方锥体[图1-3b)]。要是在承压板和试件上下 表面之间涂以油脂润滑剂,则试验加压时摩阻力将大为减少,所测得的抗压强度较低,其破 坏形态如图1-3沁)所示的开裂破坏。规定采用的方法是不加油脂润滑剂的试验方法。 承压板 均匀压应力 拉应力线 压应力线 拉 图1一3立方体抗压强度试件 )立方体试件的受力b)承压板与试件表面之间未涂润滑剂时©)承压板与试件表面之间涂润滑剂时 混凝土的抗压强度还与试件尺寸有关。试验表明 ,立方体试件尺寸愈小,摩阻力的影 愈大,测得的强度也愈高。在实际工程中也有采用边长为200mm和边长为100mm的混凝 土立方体试件,则所测得的立方体强度应分别乘以换算系数1.05和0.95来折算成边长为 150mm的混凝土立方体抗压强度。 2)混凝土轴心抗压强度(棱柱体抗压强度 通常钢筋混凝土构件的长度比它的截面边长要大得多,因此棱柱体试件(高度大于截面 边长的试件)的受力状态更接近于实际构件中混凝土的受力情况。按照与立方体试件相同条 件下制作和试验方法所得的棱柱体试件的抗压强度值,称为混凝土轴心抗压强度,用符号 表示。 试验表明,棱柱体试件的抗压强度较立方体试块的抗压强度低。棱柱体试件高度h与边 长6之比愈大 则强度愈 当hb由1增至2时,混凝土强度降低很快。但是当h/b由2 增至4时,其抗压强度变化不大(图1-4)。因为在此范围内,既可消除垫板与试件接触直 3
1-3 凝土和钢筋材料的物理力学性能(强度和变形的变化规律)的了解,则是掌握钢筋混凝土结 构的构件性能、分析和设计的基础。 1.2.1 混凝土的强度 1)混凝土立方体抗压强度 混凝土的立方体抗压强度是规定的标准试件和标准试验方法得到的混凝土强度基本代 表值。我国取用的标准试件为边长相等的混凝土立方体。这种试件的制作和试验均比较简便, 而且离散性较小。 我国国家标准《普通混凝土力学性能试验方法标准》(GB/T50081-2002)规定以每边边 长为 150mm 的立方体为标准试件,在(20±2)℃的温度和相对湿度在 95%以上的潮湿空 气中养护 28 天,依照标准制作方法和试验方法测得的抗压强度值(以 N/mm2 为单位)作为 混凝土的立方体抗压强度,用符号 fcu 表示。按这样的规定,就可以排除不同制作方法、养 护环境等因素对混凝土立方体强度的影响。 混凝土立方体抗压强度与试验方法有着密切的关系。在通常情况下,试件的上下表面与 试验机承压板之间将产生阻止试件向外自由变形的摩阻力,阻滞了裂缝的发展[图 1-3a)], 从而提高了试块的抗压强度。破坏时,远离承压板的试件中部混凝土所受的约束最少,混凝 土也剥落得最多,形成两个对顶叠置的截头方锥体[图 1-3b)]。要是在承压板和试件上下 表面之间涂以油脂润滑剂,则试验加压时摩阻力将大为减少,所测得的抗压强度较低,其破 坏形态如图 1-3c)所示的开裂破坏。规定采用的方法是不加油脂润滑剂的试验方法。 压应力线 拉应力线 摩擦力 横 向 变 形 实际压应力 上承压板 假定均匀压应力 拉 压 水平应力 ) ) ) 图 1-3 立方体抗压强度试件 a)立方体试件的受力 b)承压板与试件表面之间未涂润滑剂时 c)承压板与试件表面之间涂润滑剂时 混凝土的抗压强度还与试件尺寸有关。试验表明,立方体试件尺寸愈小,摩阻力的影响 愈大,测得的强度也愈高。在实际工程中也有采用边长为 200mm 和边长为 100mm 的混凝 土立方体试件,则所测得的立方体强度应分别乘以换算系数 1.05 和 0.95 来折算成边长为 150mm 的混凝土立方体抗压强度。 2)混凝土轴心抗压强度(棱柱体抗压强度) 通常钢筋混凝土构件的长度比它的截面边长要大得多,因此棱柱体试件(高度大于截面 边长的试件)的受力状态更接近于实际构件中混凝土的受力情况。按照与立方体试件相同条 件下制作和试验方法所得的棱柱体试件的抗压强度值,称为混凝土轴心抗压强度,用符号 fc 表示。 试验表明,棱柱体试件的抗压强度较立方体试块的抗压强度低。棱柱体试件高度 h 与边 长 b 之比愈大,则强度愈低。当 h/b 由 1 增至 2 时,混凝土强度降低很快。但是当 h/b 由 2 增至 4 时,其抗压强度变化不大(图 1-4)。因为在此范围内,既可消除垫板与试件接触面

间摩阻力对抗压强度的影响,又可以避免试件因纵向初弯曲而产生的附加偏心距对抗压强度 的影响,故所测得的棱柱体抗压强度较稳定。因此,国家标准《普通混凝土力学性能试验方 法标准》 (GB/T50081-2002)规定,混凝士的轴心抗压强度试验以150mm×150mm×300mm 的试件为标淮试件。 0051.01.52.0 3.0 4.0 n/B 图1一4/b对抗压强度的影响 3)混凝土抗拉强度 混凝士抗拉强度(用符号万表示)和抗压强度一样,都是混凝土的基本强度指标。但是 混凝土的抗拉强度比抗压强度低得多,它与同龄期混凝土抗压强度的比值大约在1/8-118。 这项比值随混凝土抗压强度等级的增大而减少,即混凝土抗拉强度的增加慢于抗压强度的增 加。 混凝土轴心受拉试验的试件可采用在两端预埋钢筋的混凝土棱柱体(图15)。试验时 用试验机的夹具夹紧试件两端外伸的钢筋能加拉力,破坏时试件在没有钢筋的中部截面被拉 断,其平均拉应力即为混凝土的轴心抗拉强度。 在用上述方法测定混凝土的轴心抗拉强度时,保持试件轴心受拉是很重要的,也是不容 易完全做到的。因为混凝士内部结构不均匀,钢筋的预埋和试件的安装都难以对中,而偏心 又对混凝土抗拉强度测试有很大的干扰,因此,目前国内外常采用立方体或圆柱体的劈裂试 验来测定混凝土的轴心抗拉强度。 · 图1一5混凝士抗拉强度试验试件(尺寸单位:mm) 劈裂试验是在卧置的立方体(或圆柱体)试件与压力机压板之间放置钢垫条及三合板(或 纤维板)垫层(图16),压力机通过垫条对试件中心面施加均匀的条形分布荷载。这样, 人
1-4 间摩阻力对抗压强度的影响,又可以避免试件因纵向初弯曲而产生的附加偏心距对抗压强度 的影响,故所测得的棱柱体抗压强度较稳定。因此,国家标准《普通混凝土力学性能试验方 法标准》(GB/T50081-2002)规定,混凝土的轴心抗压强度试验以 150mm×150mm×300mm 的试件为标准试件。 立 方 体 图 1-4 hb 对抗压强度的影响 3)混凝土抗拉强度 混凝土抗拉强度(用符号 ft 表示)和抗压强度一样,都是混凝土的基本强度指标。但是 混凝土的抗拉强度比抗压强度低得多,它与同龄期混凝土抗压强度的比值大约在 1/8~1/18。 这项比值随混凝土抗压强度等级的增大而减少,即混凝土抗拉强度的增加慢于抗压强度的增 加。 混凝土轴心受拉试验的试件可采用在两端预埋钢筋的混凝土棱柱体(图 1-5)。试验时 用试验机的夹具夹紧试件两端外伸的钢筋施加拉力,破坏时试件在没有钢筋的中部截面被拉 断,其平均拉应力即为混凝土的轴心抗拉强度。 在用上述方法测定混凝土的轴心抗拉强度时,保持试件轴心受拉是很重要的,也是不容 易完全做到的。因为混凝土内部结构不均匀,钢筋的预埋和试件的安装都难以对中,而偏心 又对混凝土抗拉强度测试有很大的干扰,因此,目前国内外常采用立方体或圆柱体的劈裂试 验来测定混凝土的轴心抗拉强度。 钢筋 钢筋 图 1-5 混凝土抗拉强度试验试件(尺寸单位:mm) 劈裂试验是在卧置的立方体(或圆柱体)试件与压力机压板之间放置钢垫条及三合板(或 纤维板)垫层(图 1-6),压力机通过垫条对试件中心面施加均匀的条形分布荷载。这样

图16劈裂试验 除垫条附近外,在试件中间垂直面上就产生了拉应力,它的方向与加载方向垂直,并且基本 上是均匀的。当拉应力达到混凝土的抗拉强度时,试件即被劈裂成两半。我国交通部部颁标 准《公路工程水泥混凝土试验规程》(JT053-94)规定,采用150mm立方块作为标准试件 进行混凝土劈裂抗拉强度测定,按照规定的试验方法操作,则混凝土劈裂抗拉强度:按下 式计算: 6、3F 0637E (1-1) 式中∫。一混凝土劈裂抗拉强度(MPa): F一劈裂破坏荷载: A一试件劈裂面面积(mm2)。 采用上述试验方法测得的混凝土劈裂抗拉强度值换算成轴心抗拉强度时,应乘以换算系 数0.9,即f=0.9fn。 4)复合应力状态下的混凝士强度 在钢筋混凝土结构中,构件通常受到轴力、弯矩、剪力及扭矩等不同组合情况的作用。 因此,混凝土更多的是处于双向或三向受力状态。在复合应力状态下,混凝土的强度有明显 变化。 对于双向正应力状态,例如,在两个互相垂直的平面上,作用着法向应力,和 ,第 三个平面上的法向应力为零。双向应力状态下混凝士强度的变化曲线如图17所示,其强度 变化特点如下: (1)当双向受压时(图17中第三象限),一向的混凝土强度随着另一向压应力的增加 雨指,/,的等于2或05时,其器度比单向抗压强度销加的为25%左右,面在“么 时,其强度增加仅为16%左右 (2)当双向受拉时(图17中第一象限),无论应力比值/,如何,实测破坏强度基 本不变,双向受拉的混凝土抗拉强度均接近于单向抗拉强度
1-5 拉 压 + 图 1-6 劈裂试验 除垫条附近外,在试件中间垂直面上就产生了拉应力,它的方向与加载方向垂直,并且基本 上是均匀的。当拉应力达到混凝土的抗拉强度时,试件即被劈裂成两半。我国交通部部颁标 准《公路工程水泥混凝土试验规程》(JTJ053-94)规定,采用 150mm 立方块作为标准试件 进行混凝土劈裂抗拉强度测定,按照规定的试验方法操作,则混凝土劈裂抗拉强度 fts 按下 式计算: 2 0.637 ts F F f A A = = (1-1) 式中 ts f —混凝土劈裂抗拉强度(MPa); F—劈裂破坏荷载; A—试件劈裂面面积(mm2)。 采用上述试验方法测得的混凝土劈裂抗拉强度值换算成轴心抗拉强度时,应乘以换算系 数 0.9,即 0.9 t ts f f = 。 4)复合应力状态下的混凝土强度 在钢筋混凝土结构中,构件通常受到轴力、弯矩、剪力及扭矩等不同组合情况的作用, 因此,混凝土更多的是处于双向或三向受力状态。在复合应力状态下,混凝土的强度有明显 变化。 对于双向正应力状态,例如,在两个互相垂直的平面上,作用着法向应力σ1 和σ2,第 三个平面上的法向应力为零。双向应力状态下混凝土强度的变化曲线如图 1-7 所示,其强度 变化特点如下: (1)当双向受压时(图 1-7 中第三象限),一向的混凝土强度随着另一向压应力的增加 而增加,σ1/σ2 约等于 2 或 0.5 时,其强度比单向抗压强度增加约为 25%左右,而在 1 2 =1 时,其强度增加仅为 16%左右。 (2)当双向受拉时(图 1-7 中第一象限),无论应力比值σ1/σ2 如何,实测破坏强度基 本不变,双向受拉的混凝土抗拉强度均接近于单向抗拉强度
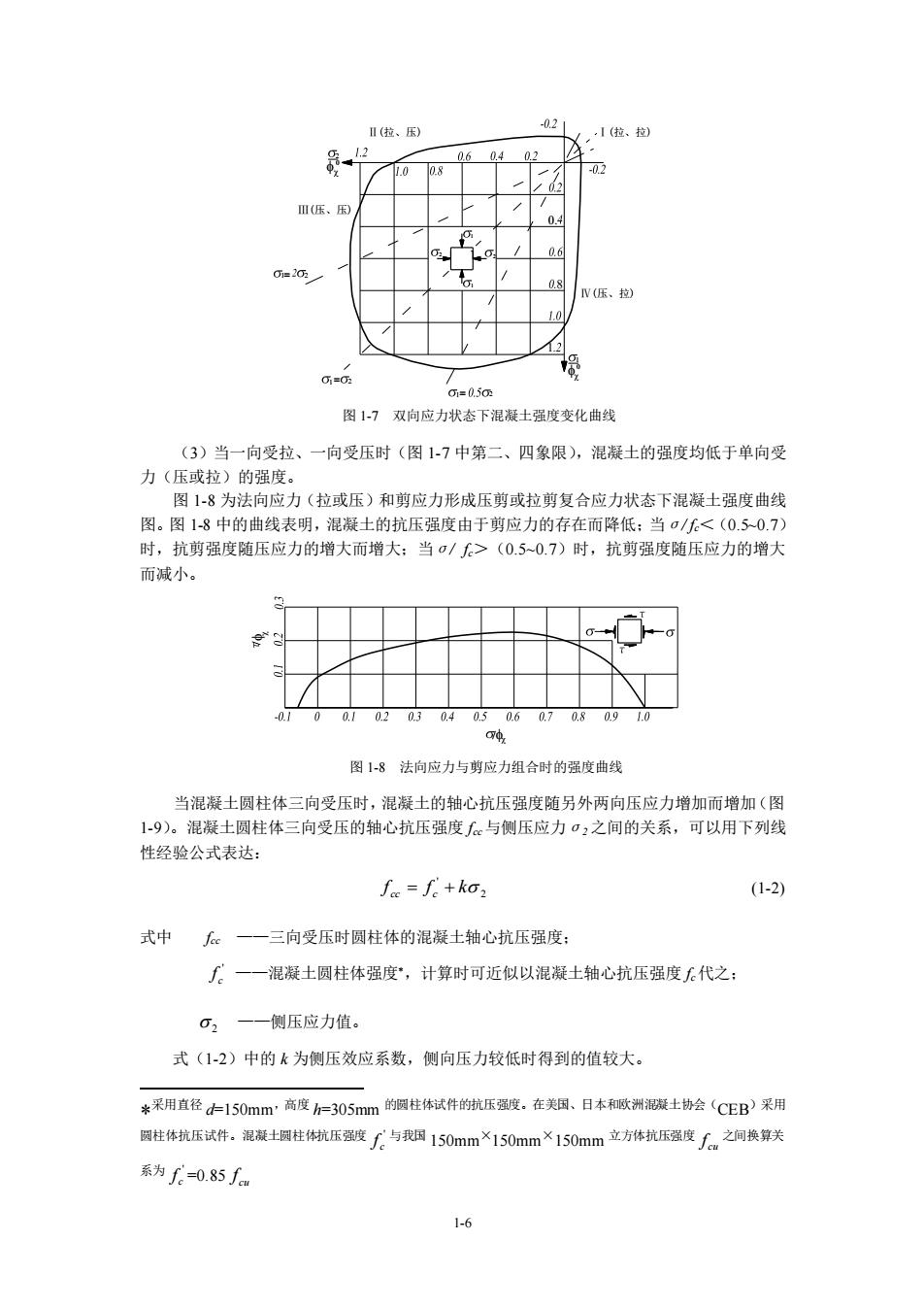
.02 拉,压) ,1(拉、拉) 压压 =050 图17双向应力状态下混凝士强度变化曲线 (3)当一向受拉、一向受压时(图17中第二、四象限),混凝土的强度均低于单向受 力(压或拉)的强度。 图1-8为法向应力(拉或压)和剪应力形成压剪或拉剪复合应力状态下混凝士强度曲线 图。图18中的曲线表明,混凝士的抗压强度由于剪应力的存在而降低:当0/C(0.50.7)时,抗剪强度随压应力的增大 而减小。 图1-8法向应力与剪应力组合时的强度曲线 当混凝土圆柱体三向受压时,混凝土的轴心抗压强度随另外两向压应力增加而增加(图 1-9。混凝土圆柱 三向受压的轴心抗压强度与侧压应力,之间的关系,可以用下列 性经验公式表达: foc=fc+ko2 (1-2) 式中 一一三向受压时圆柱体的混凝土轴心抗压强度 一一混凝土圆柱体强度·,计算时可近似以混凝土轴心抗压强度代之: 02一—侧压应力值。 式(1-2)中的k为侧压效应系数,侧向压力较低时得到的值较大。 *采用直径150mm,高度h=305mm的圆柱体试件的抗压强度.在关国、日本欧洲混凝土协会(CEB)采用 圆柱体抗压试件.混凝士柱体抗压度厂与我国150mm×150mm×150mm立方体抗压强度之间换算关 系为f=0.85∫m
1-6 = = = Ⅱ(拉、压) Ⅰ(拉、拉) Ⅲ(压、压) Ⅳ(压、拉) 图 1-7 双向应力状态下混凝土强度变化曲线 (3)当一向受拉、一向受压时(图 1-7 中第二、四象限),混凝土的强度均低于单向受 力(压或拉)的强度。 图 1-8 为法向应力(拉或压)和剪应力形成压剪或拉剪复合应力状态下混凝土强度曲线 图。图 1-8 中的曲线表明,混凝土的抗压强度由于剪应力的存在而降低;当σ/ fc<(0.5~0.7) 时,抗剪强度随压应力的增大而增大;当σ/ fc>(0.5~0.7)时,抗剪强度随压应力的增大 而减小。 图 1-8 法向应力与剪应力组合时的强度曲线 当混凝土圆柱体三向受压时,混凝土的轴心抗压强度随另外两向压应力增加而增加(图 1-9)。混凝土圆柱体三向受压的轴心抗压强度 fcc与侧压应力σ2 之间的关系,可以用下列线 性经验公式表达: 2 ' f cc = f c + k (1-2) 式中 fcc ——三向受压时圆柱体的混凝土轴心抗压强度; ' c f ——混凝土圆柱体强度,计算时可近似以混凝土轴心抗压强度 fc代之; 2 ——侧压应力值。 式(1-2)中的 k 为侧压效应系数,侧向压力较低时得到的值较大。 * 采用直径 d=150mm,高度 h=305mm 的圆柱体试件的抗压强度。在美国、日本和欧洲混凝土协会(CEB)采用 圆柱体抗压试件。混凝土圆柱体抗压强度 ' c f 与我国 150mm×150mm×150mm 立方体抗压强度 cu f 之间换算关 系为 ' c f =0.85 cu f
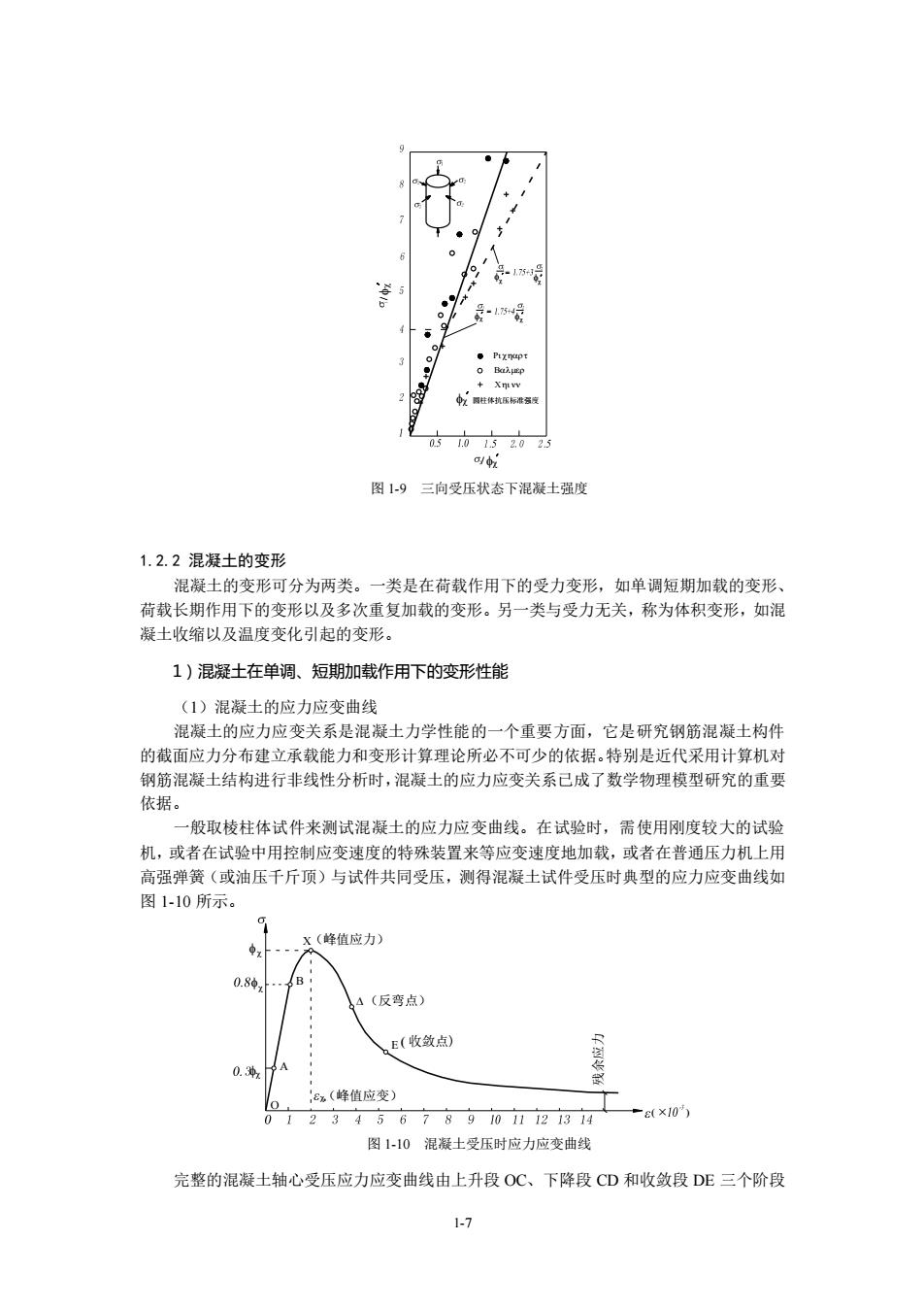
图19三向受压状态下混凝土强度 1.2.2混凝土的变形 混凝土的变形可分为两类 一类是在荷载作用下的受力变形,如单调短期加载的变形 荷载长期作用下的变形以及多次重复加载的变形。另一类与受力无关,称为体积变形,如混 凝土收缩以及温度变化引起的变形。 1)混凝土在单调、短期加载作用下的变形性能 (1)混凝土的应力应变曲线 混凝土的应力应变关系是混凝土力学性能的一个重要方面,它是研究钢筋混凝土构件 的截面应力分布建立承载能力和变形计算理论所必不可少的依据。特别是近代采用计算机对 钢筋混凝士结构进行非线性分析时,混凝土的应力应变关系己成了数学物理模型研完的重要 依据。 一般取棱柱体试件来测试混凝土的应力应变曲线。在试验时,需使用刚度较大的试验 机,或者在试验中用控制应变速度的特殊装置来等应变速度地加载,或者在普通压力机上用 高强弹簧(或油压千斤顶)与试件共同受压,测得混凝土试件受压时典型的应力应变曲线如 图1-10所示。 X(峰值应力) 4(反弯点) E(收点) (峰值应变) 1234567891011121314 图1-10混凝土受压时应力应变曲线 完整的混凝土轴心受压应力应变曲线由上升段OC、下降段CD和收敛段DE三个阶段 1.7
1-7 圆柱体抗压标准强度 = = 图 1-9 三向受压状态下混凝土强度 1.2.2 混凝土的变形 混凝土的变形可分为两类。一类是在荷载作用下的受力变形,如单调短期加载的变形、 荷载长期作用下的变形以及多次重复加载的变形。另一类与受力无关,称为体积变形,如混 凝土收缩以及温度变化引起的变形。 1)混凝土在单调、短期加载作用下的变形性能 (1)混凝土的应力应变曲线 混凝土的应力应变关系是混凝土力学性能的一个重要方面,它是研究钢筋混凝土构件 的截面应力分布建立承载能力和变形计算理论所必不可少的依据。特别是近代采用计算机对 钢筋混凝土结构进行非线性分析时,混凝土的应力应变关系已成了数学物理模型研究的重要 依据。 一般取棱柱体试件来测试混凝土的应力应变曲线。在试验时,需使用刚度较大的试验 机,或者在试验中用控制应变速度的特殊装置来等应变速度地加载,或者在普通压力机上用 高强弹簧(或油压千斤顶)与试件共同受压,测得混凝土试件受压时典型的应力应变曲线如 图 1-10 所示。 残余应力 (峰值应力) (反弯点) ( 收敛点) (峰值应变) ( × ) 图 1-10 混凝土受压时应力应变曲线 完整的混凝土轴心受压应力应变曲线由上升段 OC、下降段 CD 和收敛段 DE 三个阶段

组成。 上升段:当压应力a<0.3左右时,应力应变关系接近直线变化(O4段),混凝土处 于弹性阶段工作。在压应力口≥0.3后,随着压应力的增大,应力应变关系愈来愈偏离直线, 任一点的应变£可分为弹性应变£和塑性应变£两部分。原有的混凝土内部微裂缝发展, 并在孔隙等薄弱处产生新的个别的微裂锋。当应力法到08B点)左右后,混凝土塑性变 形显若增大 内部裂缝不断延伸扩展,并有几条贳通,应力应变曲线斜率急剧减小,如果不 继续加载,裂缝也会发展,即内部裂缝处于非稳定发展阶段。当应力达到最大应力=时 (C点),应力应变曲线的斜率己接近于水平,试件表面出现不连续的可见裂缝。 下降段:到达峰值应力点C后,混凝土的强度并不完全消失,随若应力σ的减少(氧 载),应变仍然增加,曲线下降坡度较陡,混凝土表面裂缝逐渐贯通。 收敛段:在反弯点D之后,应力下降的速率诚慢,趋于稳定的残余应力。表面纵向裂 缝把混凝土棱柱体分成若干个小柱,外载力由裂缝处的摩擦咬合力及小柱体的残余强度所承 受。 对于没有侧向约束的混凝土,收敛段没有实际意义,所以通常只注意混凝土轴心受压 应力应变曲线的上升段OC和下降段CD,而最大应力值及相应的应变值cm以及D点的 应变值(称极限压应变值:)成为曲线的三个特征值。对于均匀受压的棱柱体试件,其压 应力达到时,混凝土就不能承受更大的压力,成为结构构件计算时混凝土强度的主要指标 与£相比对应的应变随混凝土强度等级而异,约在(15、25)X103间变动,通常取 平均值为:2.0×10。应力应变曲线中相应于D的混凝士极限压应变:m约为(3.050 X103。 影响混凝土轴心受压应力应变曲线的主要因素是: ①混凝土强度。试验表明,混凝土强度对其应力应变曲线有一定影响,如图1-11所示 对于上升段,混凝土强度的影响较小,与应力峰值点相应的应变大致为0.002。随着混凝士 强度增大,则峰值点处的应变也稍大些, 对 下降段 混凝士强度则有较大影响。混凝土强 度愈高,应力应变曲线下降愈剧烈,延性就愈差(延性是材料承受变形的能力)。 0 Q00 图11强度等级不同的混凝士的应力应变曲线 ②应变速率。应变速率小,峰值应力降低,£。增大,下降段曲线坡度显著地减缓 ③测试技术和试验条件。应该采用等应变加载。如果采用等应力加载,则很难测得下 降段曲线。试验机的刚度对下降段的影响很大。如果试验机的刚度不足,在加载过程中积蓄 在压力机内的应变能立即释放所产生的压缩量,当其大于试件可能产生的变形时,结果形成 压力机的回弹对试件的冲击,使试件突然破坏,以至无法测出应力应变曲线的下降段。应变 测量的标距也有影响,应变量测的标距愈大,曲线坡度陡:标距愈小,坡度愈缓。试件端部 的约束条件对应力应变曲线下降段也有影响。例如在试件与支承垫板间垫以橡胶薄板并涂以 油脂,则与正常条件情况相比,不仅强度降低,而且没有下降段
1-8 组成。 上升段:当压应力σ<0.3fc 左右时,应力应变关系接近直线变化(OA 段),混凝土处 于弹性阶段工作。在压应力σ≥0.3fc后,随着压应力的增大,应力应变关系愈来愈偏离直线, 任一点的应变ε可分为弹性应变εce和塑性应变εcp 两部分。原有的混凝土内部微裂缝发展, 并在孔隙等薄弱处产生新的个别的微裂缝。当应力达到 0.8 fc(B 点) 左右后,混凝土塑性变 形显著增大,内部裂缝不断延伸扩展,并有几条贯通,应力应变曲线斜率急剧减小,如果不 继续加载,裂缝也会发展,即内部裂缝处于非稳定发展阶段。当应力达到最大应力σ=fc 时 (C 点),应力应变曲线的斜率已接近于水平,试件表面出现不连续的可见裂缝。 下降段:到达峰值应力点 C 后,混凝土的强度并不完全消失,随着应力σ的减少(卸 载),应变仍然增加,曲线下降坡度较陡,混凝土表面裂缝逐渐贯通。 收敛段:在反弯点 D 之后,应力下降的速率减慢,趋于稳定的残余应力。表面纵向裂 缝把混凝土棱柱体分成若干个小柱,外载力由裂缝处的摩擦咬合力及小柱体的残余强度所承 受。 对于没有侧向约束的混凝土,收敛段没有实际意义,所以通常只注意混凝土轴心受压 应力应变曲线的上升段 OC 和下降段 CD,而最大应力值 fc及相应的应变值εco 以及 D 点的 应变值(称极限压应变值εcu)成为曲线的三个特征值。对于均匀受压的棱柱体试件,其压 应力达到 fc时,混凝土就不能承受更大的压力,成为结构构件计算时混凝土强度的主要指标。 与 fc相比对应的应变εco 随混凝土强度等级而异,约在(1.5~2.5)×10-3 间变动,通常取其 平均值为εco=2.0×10-3。应力应变曲线中相应于 D 的混凝土极限压应变εcu 约为(3.0~5.0) ×10-3。 影响混凝土轴心受压应力应变曲线的主要因素是: ①混凝土强度。试验表明,混凝土强度对其应力应变曲线有一定影响,如图 1-11 所示。 对于上升段,混凝土强度的影响较小,与应力峰值点相应的应变大致为 0.002。随着混凝土 强度增大,则峰值点处的应变也稍大些。对于下降段,混凝土强度则有较大影响。混凝土强 度愈高,应力应变曲线下降愈剧烈,延性就愈差(延性是材料承受变形的能力)。 = ( ) 图 1-11 强度等级不同的混凝土的应力应变曲线 ②应变速率。应变速率小,峰值应力 fc降低,εco 增大,下降段曲线坡度显著地减缓。 ③测试技术和试验条件。应该采用等应变加载。如果采用等应力加载,则很难测得下 降段曲线。试验机的刚度对下降段的影响很大。如果试验机的刚度不足,在加载过程中积蓄 在压力机内的应变能立即释放所产生的压缩量,当其大于试件可能产生的变形时,结果形成 压力机的回弹对试件的冲击,使试件突然破坏,以至无法测出应力应变曲线的下降段。应变 测量的标距也有影响,应变量测的标距愈大,曲线坡度陡;标距愈小,坡度愈缓。试件端部 的约束条件对应力应变曲线下降段也有影响。例如在试件与支承垫板间垫以橡胶薄板并涂以 油脂,则与正常条件情况相比,不仅强度降低,而且没有下降段

(2)混凝土的弹性模量、变形模量 在实际工程中,为了计算结构的变形,必须要求一个材料常数一一弹性模量。而混凝 土的 ]应变的比值并非一个常数,是随着混凝士的应力变化而变化,所以混凝土弹性模量 的取值比钢材复杂得多 混凝土的弹性模量有三种表示方法(图1-12) 图1-2混凝土变形模量的表示方注 ①原点弹性模 在混凝土受压应力应变曲线图的原点作切线,该切线的斜率即为原点弹性模量。即 Er==tan do (1-3) ②切线模量 在混凝土应力应变曲线上某一应力。处作一切线,该切线的斜率即为相应于应力 时的切线模量,即 E.=do de (14) ③变形模量 连接混凝土应力应变曲线的原点O及曲线上某一点K作割线,K点混凝土应力为· (0.5),则该割线(O水)的斜率即为变形模量,也称割线模量或弹塑性模量,即 B.tana-c (1-5) 在某一应力e 下,混凝土应变:由弹性应变和塑性应变e组成,于是混凝士的 变形模量与原点弹性模量的关系为 B:-de=.d= (1-6) 8e6.8x 式中的为弹性特征系数,即yy么。弹性特征系数7与应力值有关,当0,≤05时, 1.9
1-9 (2)混凝土的弹性模量、变形模量 在实际工程中,为了计算结构的变形,必须要求一个材料常数——弹性模量。而混凝 土的应力应变的比值并非一个常数,是随着混凝土的应力变化而变化,所以混凝土弹性模量 的取值比钢材复杂得多。 混凝土的弹性模量有三种表示方法(图 1-12) = = 图 1-12 混凝土变形模量的表示方法 ①原点弹性模量 在混凝土受压应力应变曲线图的原点作切线,该切线的斜率即为原点弹性模量。即 0 ' tan = = ce Ec (1-3) ②切线模量 在混凝土应力应变曲线上某一应力σc 处作一切线,该切线的斜率即为相应于应力σc 时的切线模量,即 d E d c = '' (1-4) ③变形模量 连接混凝土应力应变曲线的原点 O 及曲线上某一点 K 作割线,K 点混凝土应力为σc (=0.5 fc),则该割线(OK)的斜率即为变形模量,也称割线模量或弹塑性模量,即 c c Ec = 1 = ''' tan (1-5) 在某一应力σc下,混凝土应变εc由弹性应变εce和塑性应变εcp 组成,于是混凝土的 变形模量与原点弹性模量的关系为 ''' ' c ce c c ce c c Ec E = = = (1-6) 式中的 为弹性特征系数,即 = c ce 。弹性特征系数 与应力值有关,当σc≤0.5 fc时
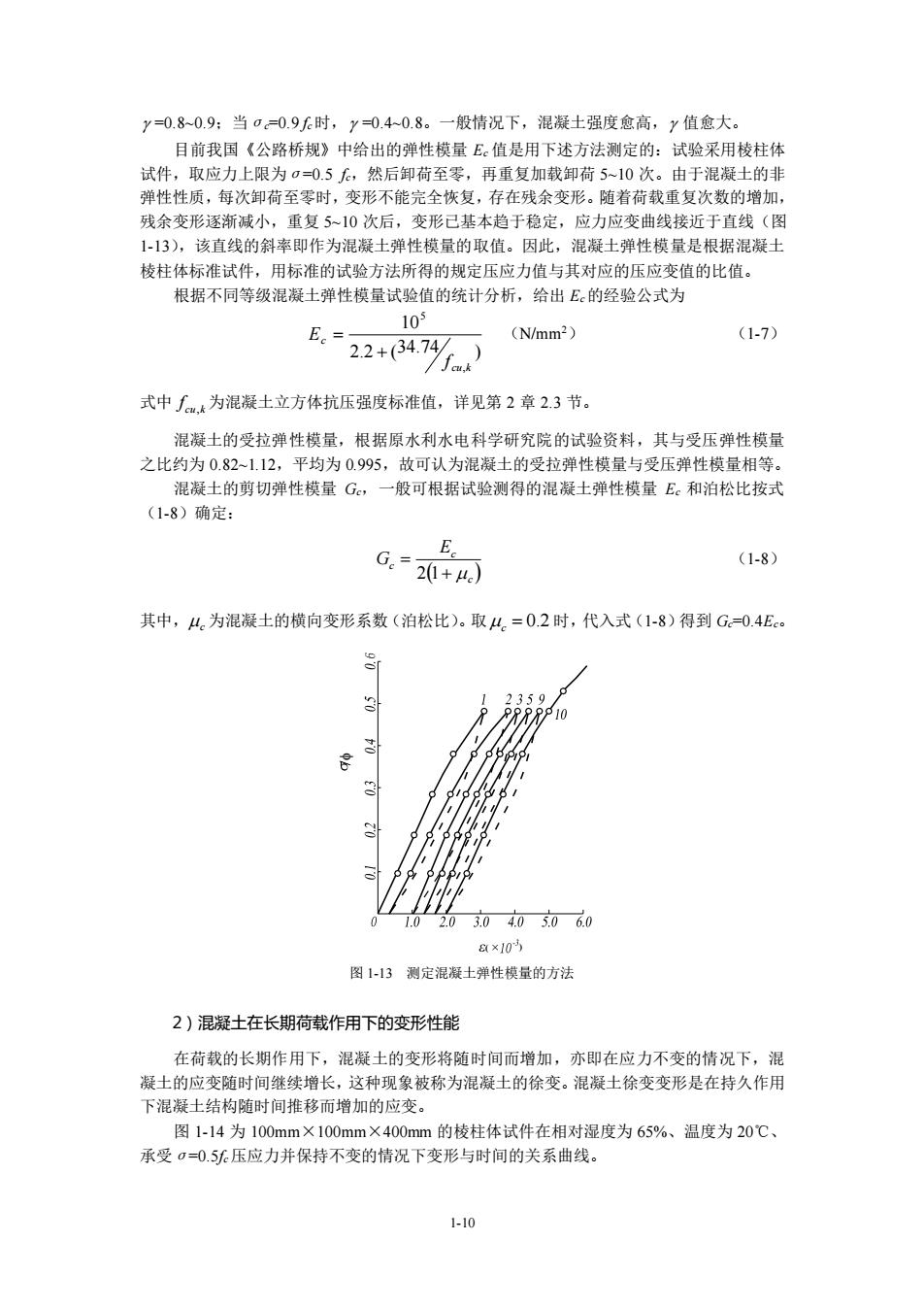
y=0.80.9:当0=0.9时,y0.40.8。一般情况下,混凝土强度愈高,y值愈大。 目前我国《公路桥规》中给出的弹性模量E。值是用下述方法测定的:试验采用棱柱体 试件,取应力上限为05,然后卸荷至零,再重复加载卸荷510次。由于混凝土的 弹性性质,每次卸荷至零时,变形不能完全恢复,存在残余变形。随着荷截重复次数的增加 残余变形逐渐减小,重复5~10次后,变形已基本趋于稳定,应力应变曲线接近于直线(图 1-13),该直线的斜率即作为混凝土弹性模量的取值。因此,混凝士弹性模量是根据混凝士 棱柱体标准试件,用标准的试验方法所得的规定压应力值与其对应的压应变值的比值。 根据不同等级混凝土弹性模量试验值的统计分析,给出E的经验公式为 105 Ec= (N/mm2) (1-7) 2.2+(34.74 6 式中厂为混凝土立方体抗压强度标准值,详见第2章2.3节。 混凝土的受拉弹性模量,根据原水利水电科学研究院的试验资料,其与受压弹性模量 之比约为0.82-1.12,平均为0995,故可认为混凝士的受拉弹性模量与受压弹性模量相等。 混凝土的剪切弹性模量G,一般可根据试验测得的混凝土弹性模量E。和泊松比按式 (1-8)确定: G.=20+4.) (1-8) 其中,4.为混凝土的横向变形系数(泊松比)。取4=02时,代入式(1-8)得到G0.4E 359 .0 200405060 8×10 图113测定混凝土弹性模量的方法 2)混凝土在长期荷载作用下的变形性能 凝士的应变随时间继续增长 下混凝土结构随时间推移而增加的应变。 图1-14为100mm×100mm×400mm的棱柱体试件在相对湿度为65%、温度为20℃、 承受σ=0.5水压应力并保持不变的情况下变形与时间的关系曲线。 1-10
1-10 =0.8~0.9;当σc=0.9 fc时, =0.4~0.8。一般情况下,混凝土强度愈高, 值愈大。 目前我国《公路桥规》中给出的弹性模量 Ec 值是用下述方法测定的:试验采用棱柱体 试件,取应力上限为σ=0.5 fc,然后卸荷至零,再重复加载卸荷 5~10 次。由于混凝土的非 弹性性质,每次卸荷至零时,变形不能完全恢复,存在残余变形。随着荷载重复次数的增加, 残余变形逐渐减小,重复 5~10 次后,变形已基本趋于稳定,应力应变曲线接近于直线(图 1-13),该直线的斜率即作为混凝土弹性模量的取值。因此,混凝土弹性模量是根据混凝土 棱柱体标准试件,用标准的试验方法所得的规定压应力值与其对应的压应变值的比值。 根据不同等级混凝土弹性模量试验值的统计分析,给出 Ec的经验公式为 ) 34.74 2.2 ( 10 , 5 cu k c f E + = (N/mm2) (1-7) 式中 cu k f , 为混凝土立方体抗压强度标准值,详见第 2 章 2.3 节。 混凝土的受拉弹性模量,根据原水利水电科学研究院的试验资料,其与受压弹性模量 之比约为 0.82~1.12,平均为 0.995,故可认为混凝土的受拉弹性模量与受压弹性模量相等。 混凝土的剪切弹性模量 Gc,一般可根据试验测得的混凝土弹性模量 Ec 和泊松比按式 (1-8)确定: ( ) c c c E G + = 2 1 (1-8) 其中, c 为混凝土的横向变形系数(泊松比)。取 c = 0.2 时,代入式(1-8)得到 Gc=0.4Ec。 ( × ) 图 1-13 测定混凝土弹性模量的方法 2)混凝土在长期荷载作用下的变形性能 在荷载的长期作用下,混凝土的变形将随时间而增加,亦即在应力不变的情况下,混 凝土的应变随时间继续增长,这种现象被称为混凝土的徐变。混凝土徐变变形是在持久作用 下混凝土结构随时间推移而增加的应变。 图 1-14 为 100mm×100mm×400mm 的棱柱体试件在相对湿度为 65%、温度为 20℃、 承受σ=0.5fc压应力并保持不变的情况下变形与时间的关系曲线