
§3.2连续型随机变量 在第二章里,己经对离散型随机变量作了一些研究,下面将要研究另一类十分重要而且常 见的随机变量 连续型随机变量 定义3.2若5()是随机变量,F(x)是它的分布函数,如果存在函数px),使对任意的x有 F(x)=p(y)dy (3.12) 则称(o)对连续型随机变量,相应的Fx)为连续型分布函数,同时称P(x)是F(x)的橛率密度 函数或简称为密度 由分布函数的性质即可验证任一连续型分布的密度函数(x)必具有下述性质: ()px)≥0 (3.13) (2)广px)t=l (3.14) 反过来,任意一个R上的函数P(x,如果具有以上的两个性质,即可由(3.12)式定义一个分 布函数Fx) 如果随机变量(@)的密度函数x,则对任意的x,x(<x)有 p(xs(@)<x2)=F(x2)-F(x) ="p(y)dy (3.15) 这一结果有很简单的几何意义:5(@)落在[xx2)中的概率,恰好等于在区间[xx2)上由曲 线y=p(x)形成的曲边梯形的面积 由(3.15)式还可以证明,连续型随机变量(@)取单点值的概率为零,也就是说对任意的 xp5(o)=x)=0于是有 px≤5(o)sx2)=px1≤5(o)<x2)+p(5(o)=x2) p(x 5(@)<x:)=[p(y)dy (3,16)
§ 3.2 连续型随机变量 在第二章里,已经对离散型随机变量作了一些研究,下面将要研究另一类十分重要而且常 见的随机变量-----连续型随机变量. 定义 3.2 若 () 是随机变量,F(x)是它的分布函数,如果存在函数 p(x),使对任意的 x 有 − = x F(x) p(y)dy (3.12) 则称 () 对连续型随机变量,相应的 F(x)为连续型分布函数,同时称 P(x)是 F(x)的概率密度 函数或简称为密度. 由分布函数的性质即可验证任一连续型分布的密度函数 p(x)必具有下述性质: (1) p(x) 0; (3.13) (2) − p(x)dx =1 (3.14) 反过来,任意一个 R 上的函数 P(x),如果具有以上的两个性质,即可由(3.12)式定义一个分 布函数 F(x), 如 果 随 机 变 量 () 的 密 度 函 数 P(x), 则 对 任 意 的 , ( ) 1 2 1 2 x x x x 有 ( ( ) ) ( ) ( ) 1 2 2 1 p x x = F x − F x = 2 1 ( ) x x p y dy (3.15) 这一结果有很简单的几何意义: () 落在[ ) 1 2 x x 中的概率,恰好等于在区间[ ) 1 2 x x 上由曲 线 y = p(x) 形成的曲边梯形的面积, 由(3.15)式还可以证明,连续型随机变量 () 取单点值的概率为零,也就是说对任意的 x, p( () = x) = 0 于是有 ( ( ) ) 1 2 p x x ( ( ) ) ( ( ) ) 1 2 2 = p x x + p = x = 2 1 ( ( ) ) ( ) 1 2 x x p x x p y dy (3.16)
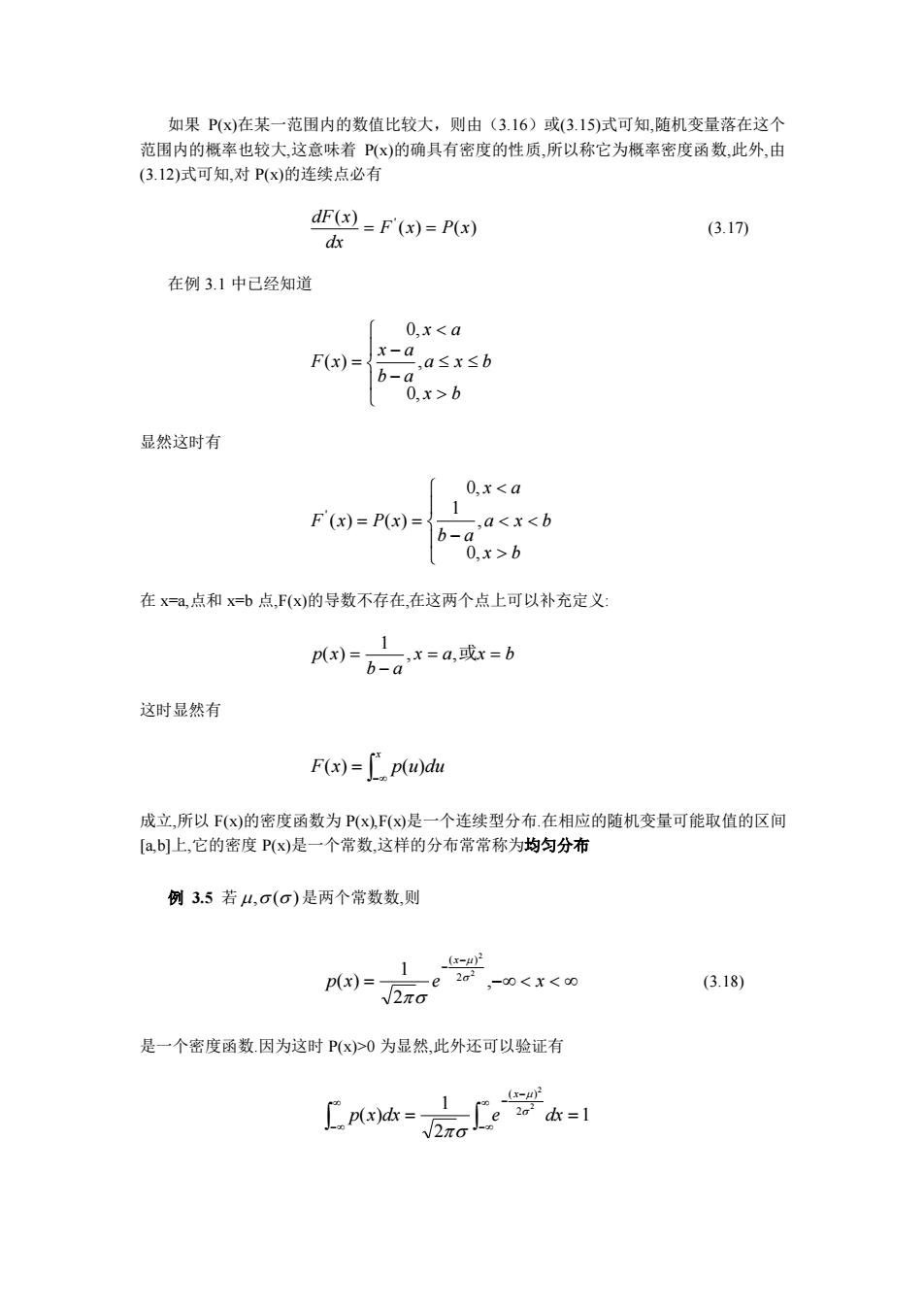
如果P(x)在某一范围内的数值比较大,则由(3.16)或(3.15)式可知,随机变量落在这个 范围内的概率也较大,这意味者(x)的确具有密度的性质,所以称它为概率密度函数,此外,庄 (3.12)式可知,对P(x)的连续点必有 dF(x)=F(x)=P(x) (3.17 dx 在例3.1中己经知道 0,xb 显然这时有 ,xb 在x=a点和x=b点,F(x)的导数不存在,在这两个点上可以补充定义: p代)=b-ax=a,或x=b 这时显然有 Fx)=广pw)du 成立,所以F(x)的密度函数为P(x,F(x)是一个连续型分布在相应的随机变量可能取值的区间 [a,b]上,它的密度P(x)是一个常数,这样的分布常常称为均匀分布 例3.5若4,o(o)是两个常数数,则 -00为显然此外还可以验证有
如果 P(x)在某一范围内的数值比较大,则由(3.16)或(3.15)式可知,随机变量落在这个 范围内的概率也较大,这意味着 P(x)的确具有密度的性质,所以称它为概率密度函数,此外,由 (3.12)式可知,对 P(x)的连续点必有 ( ) ( ) ( ) ' F x P x dx dF x = = (3.17) 在例 3.1 中已经知道 − − = x b a x b b a x a x a F x 0, , 0, ( ) 显然这时有 − = = x b a x b b a x a F x P x 0, , 1 0, ( ) ( ) ' 在 x=a,点和 x=b 点,F(x)的导数不存在,在这两个点上可以补充定义: x a x b b a p x = = − = , ,或 1 ( ) 这时显然有 − = x F(x) p(u)du 成立,所以 F(x)的密度函数为 P(x),F(x)是一个连续型分布.在相应的随机变量可能取值的区间 [a,b]上,它的密度 P(x)是一个常数,这样的分布常常称为均匀分布 例 3.5 若 , ( ) 是两个常数数,则 = − − − p x e x x , 2 1 ( ) 2 2 2 ( ) (3.18) 是一个密度函数.因为这时 P(x)>0 为显然,此外还可以验证有 1 2 1 ( ) 2 2 2 ( ) = = − − − − p x dx e dx x

为t可号=y测 上学片 这时有 HL-iLwEw 品工re等h 现在作坐标变换,令 y=rsme 所以有 2-eo1 于是 [p(xyx=1 这个函数称为正态密度,相应的分布函数为 (3.19) 并称Fx)为正态分布,常常简单地记作N(4,G2)如果一个随机变量(O)的分布函数是正态 分布.也称(回)是一个正态变量.N(0,1)分布常常称为是标准下态分布,其密度函数通常 以(x)表示,相应的分布函数则记作(x),所以
为此,可令 y x = − ,则 e dx e dy x y − − − − − = 2 2 ( ) 2 2 2 2 1 2 1 这时有 − − − − − − = • e dy e dx e dy y x y 2 2 2 2 2 2 2 2 1 2 1 − − + − = e dxdy x y 2 2 2 2 2 现在作坐标变换,令 = = sin cos y r x r 所以有 1 2 1 2 1 2 0 0 2 2 2 2 2 = == − − − e dy e rdr d y r 于是 ( ) =1 − p x dx 这个函数称为正态密度,相应的分布函数为 − − − = − x y F x e dy, x 2 1 ( ) 2 2 2 ( ) (3.19) 并称 F(x)为正态分布,常常简单地记作 ( , ) 2 N 如果一个随机变量 () 的分布函数是正态 分布.也称 () 是一个正态变量.N(0,1)分布常常称为是标准下态分布,其密度函数通常 以 (x) 表示,相应的分布函数则记作 (x) ,所以

-L0ww-ze5本 (3.23) 设E是N(4,σ2)分布的随机变量,则 =aLe 这时令 7=4 (3.24 则)也是一个随机变量,并且有 0<=。<5<+川 对上选风作支量提令加=名每烟 pg<方上e加=w 由此可见,刀服从N(O,1)分布的标准态态随机变量.于是,要查F(x)=P(5<x,只要查 0,其中y=一上这时只要查N0,1)表,因为这时有 =5<=。<号) 两边求导还有
− − − = = x y x x y dy e dy 2 2 2 1 ( ) ( ) (3.23) 设 是 ( , ) 2 N 分布的随机变量,则 − − − = x y p x e dy 2 2 2 ( ) 2 1 ( ) 这时令 − = (3.24) 则 也是一个随机变量,并且有 ( ) ( ) = + − p x = p x p x + − − − = x dy y e 2 2 2 ( ) 2 1 对上述积分作变量替换,令 − = y 即得 − − = = x p x e du (x) 2 1 ( ) 2 2 由此可见, 服从 N(0,1)分布的标准态态随机变量.于是,要查 F(x) = p( x), 只要查 ( y),其中 − = x y 这时只要查 N(0,1)表,因为这时有 − − = = x F(x) p( x) p − = − x x p 两边求导还有

=F=2) 所以一张N(0,1)长解决了所有N(4,c2)分布的查表问题
− = = x p x F x ( 1 ( ) ( ) ' 所以一张 N(0,1)长解决了所有 ( , ) 2 N 分布的查表问题