
§1.6独立性 在上一节中我们知道了条件概率这个概念,在以知事件A发生的条件下,B发生的可能性 味条件概率 P (BIA)=P(AB) P(4A) 并日由此得到了一般的概率乘法公式: 事实上事件B的发生不受A的影响。 也就是意味者 =P (BIA 有此启示我们引入下述定义: 定义1.5对任意的两个事件A、B,若 P(AB)=P(A)·P(B) 成立,则称事件A、B相互独立,简称为独立的 这一事实读者不会感到意外,因为必然事件?与不可能事件⑦的发生与否,的确是不受任 何事件影响的,也不影响其他事件是否发生。 例题略(见书P42) 现在我们己经知道当事件A、B互不相容时,有加法公式: P(AB)=P (A)+P (B) 如果事件A与B互相独立,则有乘法公式P(AB)=P(A)P(B) 这两个公式的外形是很类式的加法公式,而令一个是关于积的乘法公式。由概率的有限可加 性已知加法公式对任意有限个事件都成立,例如有A、B、C三个事件,它们两两互不相容 引例从一付52张的扑克牌中任意抽取一张,以A表示抽出一张A,以B表示抽出一张思 桃,问A与B是否独立? 定理、以下四件事等价: ()事件A、B相互独立:(2)事件A、B相互独立: (3)事件A、B相互独立:(4)事件A、B相互独立。二、多个事件的独立定义若三个事件 A、B、C满足: (1)P(AB)=P(A)P(B), P(AC)=P(A)P(C) P(BCFP(B)P(C) 则称事件A、B、C两两相互独立:若在此基础上还满足: (2)P(ABC)=P(A)P(B)P(C). 则称事件A、B、C相互独立。一般地,设A1,A2,,An是n个事件,如果对任意k(I<kE, 任意的1i1<i2<·<i认£n,具有等式 =P(A P(A2) PAik)则称n个事件A1,A2,,An相互独立。 立性的应用1、加法公式的简化:若事件A1,A2,,An相互独 这时就 P(AUBUC)=P(A)+P(B)+P(C) 由两个公式的相似外形,你可能会产生一种猜测:如果事件A,B,C两两独立,就有乘法公 P(AUBUC)=P(A)+P(B)+P(C) 成立。遗憾的是这个猜测一般说来并不成立。事件A,B,C两两独立,依定义有下述三个 等式:
§1.6 独立性 在上一节中我们知道了条件概率这个概念,在以知事件 A 发生的条件下,B 发生的可能性 味条件概率 P(B|A)= ( ) ( ) P A P AB 并且由此得到了一般的概率乘法公式: 事实上事件 B 的发生不受 A 的影响,也就是意味着 P(B)=P(B|A) 有此启示我们引入下述定义: 定义 1.5 对任意的两个事件 A、B,若 P(AB)=P(A)·P(B) 成立,则称事件 A、B 相互独立,简称为独立的。 这一事实读者不会感到意外,因为必然事件 与不可能事件 的发生与否,的确是不受任 何事件影响的,也不影响其他事件是否发生。 例题略(见书 P42) 现在我们已经知道当事件 A、B 互不相容时,有加法公式: P(A B)=P(A)+P(B) 如果事件 A 与 B 互相独立,则有乘法公式 P(AB)=P(A)P(B) 这两个公式的外形是很类式的加法公式,而令一个是关于积的乘法公式。由概率的有限可加 性已知加法公式对任意有限个事件都成立,例如有 A、B、C 三个事件,它们两两互不相容 引例 从一付 52 张的扑克牌中任意抽取一张,以 A 表示抽出一张 A,以 B 表示抽出一张黑 桃,问 A 与 B 是否独立? 定理、以下四件事等价: (1)事件 A、B 相互独立;(2)事件 A、B 相互独立; (3)事件 A、B 相互独立;(4)事件 A、B 相互独立。二、多个事件的独立定义 若三个事件 A、B、C 满足: (1) P(AB)=P(A)P(B), P(AC)=P(A)P(C), P(BC)=P(B)P(C), 则称事件 A、B、C 两两相互独立;若在此基础上还满足: (2)P(ABC)=P(A)P(B)P(C), 则称事件 A、B、C 相互独立。一般地,设 A1,A2,…,An 是 n 个事件,如果对任意 k (1<k£n), 任意的 1£i1<i2 <… < ik£n,具有等式 P(A i1 A i2 … A ik)=P(A i1)P(A i2)…P(A ik) 则称 n 个事件 A1,A2,…,An 相互独立。 三、事件独立性的应用 1、加法公式的简化:若事件 A1,A2,…,An 相互独立, 这时就 有 P(A∪B∪C)=P(A)+P(B)+P(C) 由两个公式的相似外形,你可能会产生一种猜测:如果事件 A,B,C 两两独立,就有乘法公 式 P(A∪B∪C)=P(A)+P(B)+P(C) 成立。遗憾的是这个猜测一般说来并不成立。事件 A,B,C 两两独立,依定义有下述三个 等式:

P(AB)=P(A)P(B) P(BC)=P(B)P(C) (L.18) P(CA)=P(C)P(A) 同时成立,但是由这三个等式并不能保证 P(ABC)=P(AP(B)P(C) (1.19) 也一定成立下面的例子证实了这一点 例1.22设样本空间Q={“1,02,3,“4)含有等可能的罡个基本事件,又 A={u1,02 B={d1.o3 C={w1,u4} 显然有 P(A)=P(B)=P(C)=2/4=1/2 并且容易验证这时(1.18)的三个等式均成立,但 ABC=1 所以 PABC)=IA≠PA)PB)P(C) 反过来,由P(ABC)=P(A)P(B)PC)成立,也不能保证(1.18)的三个式子一定成立(习 题1.38).为此,对三个事件的独立性就要求(1.18)和(1.19)都成立.所以有下述定义 定义1.6对任意三个事件A,B,C,如果有 P(AB)=P(A)P(B) P(BC)=P(B)P(C) (1.20) P(CA)=P(CIP(AY P(ABC)=P(A)P(B)P(C) 四个同时成立,则称事件A,B,C相互独立 现在可以讨论一般的情形.设A,A2,An是n个事件,如果对于任意的k(I<k≤n)和任 意的一组1≤<<<14≤n,等有等式 P(AA2…Ai,)=P(A)P(A3)…p(Ai.)(1.21) 成立,则称A,A,…A是n个相互独立的事件由此可知,n个事件的相互独立性,需要有 2日-2--1 个等式来保证 在前面的讨论中已经指出,事件的独立性可以使得实际问题的计算得简化.下面便是生 个应用的例子 例1.23用2如个相同的元件(例如整流二极管)组成一个系统有两种不同的联结方式
P(CA) = P(C)P(A) P(BC) = P(B)P(C) P(AB) = P(A)P(B) (1.18) 同时成立,但是由这三个等式并不能保证 P(ABC)=P(A)P(B)P(C) (1.19) 也一定成立.下面的例子证实了这一点. 例 1.22 设样本空间Ω={ω1,ω2,ω3, ω4} 含有等可能的罡个基本事件,又 A={ω1, ω2} B={ω1, ω3} C={ω1, ω4} 显然有 P(A)=P(B)=P(C)=2/4=1/2 并且容易验证这时(1.18)的三个等式均成立, 但 ABC={ω1} 所以 P(ABC)=1/4≠P(A)P(B)P(C) 反过来,由 P(ABC)= P(A)P(B)P(C)成立,也不能保证(1.18)的三个式子一定成立(习 题 1.38).为此,对三个事件的独立性就要求(1.18)和(1.19).都成立.所以有下述定义: 定义 1.6 对任意三个事件 A,B,C,如果有 P(ABC) = P(A)P(B)P(C) P(CA) = P(C)P(A) P(BC) = P(B)P(C) P(AB) = P(A)P(B) (1.20) 四个同时成立,则称事件 A,B,C 相互独立. 现在可以讨论一般的情形.设 A1,A2,…,An 是 n 个事件,如果对于任意的 k (1<k≤n)和任 意的一组 1≤ 1 i < 2 i <…< k i ≤n,等有等式 P( Ai1 Ai2 … n Ai )=P( Ai1 )P( Ai2 )…P( n Ai ) (1.21) 成立,则称 A1 , A2… An 是 n 个相互独立的事件.由此可知,n 个事件的相互独立性,需要有 2 1 2 = − − = n n n k n k 个等式来保证. 在前面的讨论中已经指出,事件的独立性可以使得实际问题的计算得简化.下面便是生 个应用的例子. 例 1.23 用 2n 个相同的元件(例如整流二极管)组成一个系统,有两种不同的联结方式
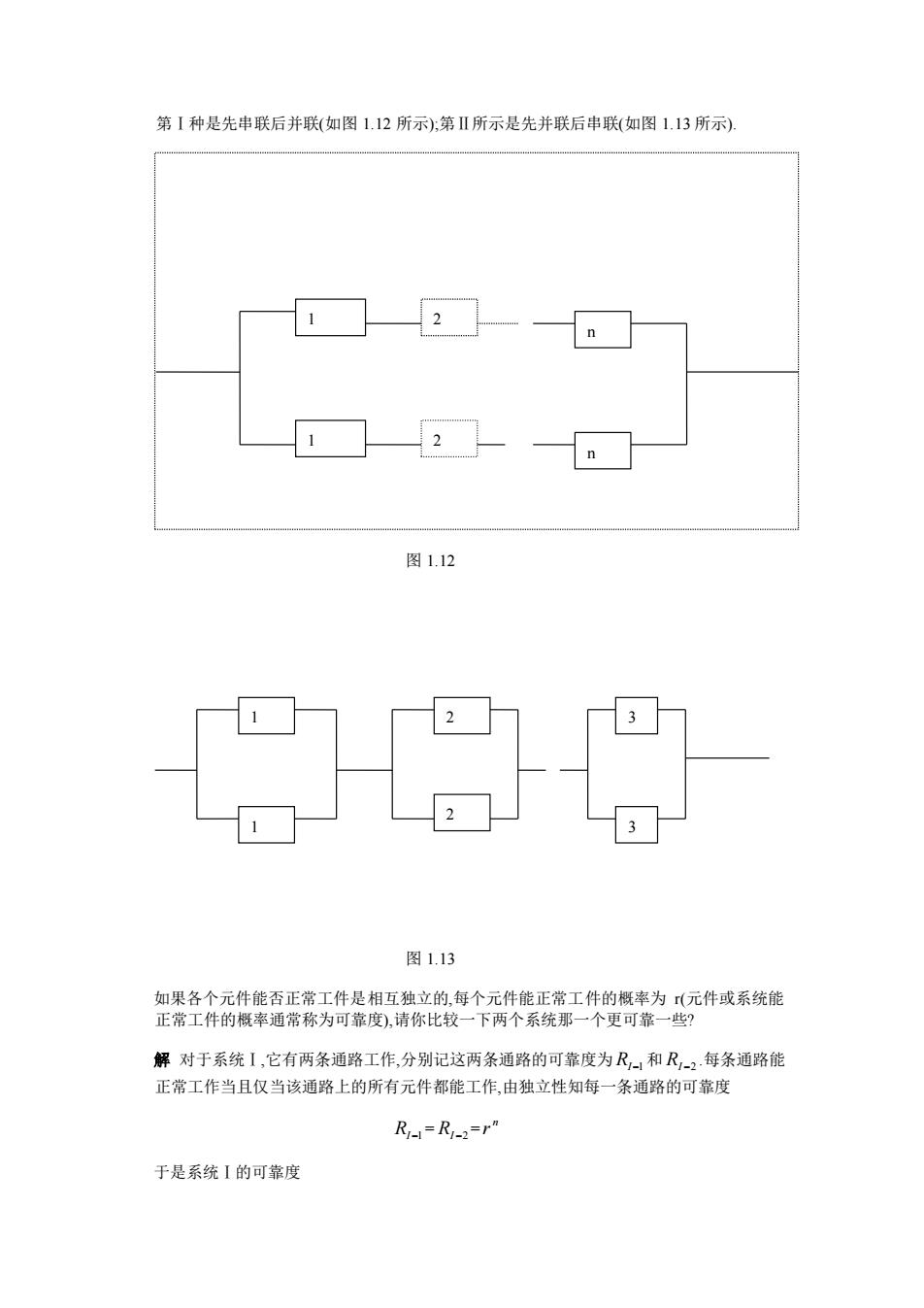
第1种是先串联后并联(如图1,12所示)第Ⅱ所示是先并联后串联(如图1.13所示) 2. n 1☐2 n 图112 图1.13 如果各个元件能否正常工件是相互独立的,每个元件能正常工件的概率为(元件或系统能 正常工件的概率通常称为可靠度),请你比较一下两个系统那一个更可靠一些? 解对于系统I,它有两条通路工作,分别记这两条通路的可靠度为R和R-2每条通路能 正常工作当且仅当该通路上的所有元件都能工作,由独立性知每一条通路的可靠度 R=R-2=r" 于是系统I的可靠度
第Ⅰ种是先串联后并联(如图 1.12 所示);第Ⅱ所示是先并联后串联(如图 1.13 所示). 图 1.12 图 1.13 如果各个元件能否正常工件是相互独立的,每个元件能正常工件的概率为 r(元件或系统能 正常工件的概率通常称为可靠度),请你比较一下两个系统那一个更可靠一些? 解 对于系统Ⅰ,它有两条通路工作,分别记这两条通路的可靠度为 RI −1 和 RI −2 .每条通路能 正常工作当且仅当该通路上的所有元件都能工作,由独立性知每一条通路的可靠度 RI −1 = RI −2 = n r 于是系统Ⅰ的可靠度 1 1 2 2 n n 1 1 2 2 3 3

R=l-(1-R1-R-2) =1-(1-r")2=r(2-) 对于系统Ⅱ,先求每一个并联的小节(如图1.14)的可靠度,由独立性知每一个小节的可靠度 R-4=l-(l-0)2=r2-rh1≤i≤n 而整个系统由相同的个小节串联而成,再一次利用独立性能即可得到系统Ⅱ的可靠度为 Rn Ro-Rn-2...Ra-n =[(2-r月”=r(2-r) 利用数学归纳法,可以证明当≥2时,总有 (2-)">2-r” 成立.从而当n≥2,有Ra>R,即系统Ⅱ比系统I更可靠些 这是一个师有启发性的子田相同的元件组成一个系统完成相同的功能只是由干 设计的联结方式不同,得到的可靠度就不同。从而告诚我们,事先应精心设计以提高产品 (或工程)的可靠度,这是可靠性工程学中的一个重要课题
R1 =1-(1- RI −1 )(1- RI −2 ) = 1-(1- n r ) 2 = (2 ) n n r − r 对于系统Ⅱ,先求每一个并联的小节(如图 1.14)的可靠度,由独立性知每一个小节的可靠度 RⅡ−i =1-(1-r) 2 =r(2-r), 1≤i≤n 而整个系统由相同的 n 个小节串联而成,再一次利用独立性能即可得到系统Ⅱ的可靠度为 RⅡ = RⅡ−1 RⅡ−2RⅡ−n . = n n n [r(2 − r)] = r (2 − r) 利用数学归纳法,可以证明当 n≥2 时,总有 (2-r) n >2- n r 成立.从而当 n≥2,有 RⅡ RⅠ,即系统Ⅱ比系统Ⅰ更可靠些. 这是一个颇有启发性的例子.用相同的元件组成一个系统,完成相同的功能,只是由于 设计的联结方式不同,得到的可靠度就不同.从而告诫我们,事先应精心设计以提高产品 (或工程)的可靠度,这是可靠性工程学中的一个重要课题