
第五章 非平稳序列的随机分析
第五章 非平稳序列的随机分析

本章结构 ■差分运算 ■ARIMA模型 ■Auto-Regressive模型 ■异方差的性质 ■方差齐性变化 ■条件异方差模型
本章结构 差分运算 ARIMA模型 Auto-Regressive模型 异方差的性质 方差齐性变化 条件异方差模型

5.1差分运算 ■差分运算的实质 ■差分方式的选择 ■过差分
5.1 差分运算 差分运算的实质 差分方式的选择 过差分

差分运算的实质 差分方法是一种非常简便、有效的确定 性信息提取方法 ■Cramer分解定理在理论上保证了适当阶 数的差分一定可以充分提取确定性信息 ■差分运算的实质是使用自回归的方式提 取确定性信息 x=(1-Bx=-C
差分运算的实质 差分方法是一种非常简便、有效的确定 性信息提取方法 Cramer分解定理在理论上保证了适当阶 数的差分一定可以充分提取确定性信息 差分运算的实质是使用自回归的方式提 取确定性信息 d i t i i d i t d t d x B x C x 0 (1 ) ( 1)

差分方式的选择 序列蕴含着显著的线性趋势,一阶差分 就可以实现趋势平稳 ■ 序列蕴含着曲线趋势,通常低阶(二阶 或三阶)差分就可以提取出曲线趋势的 影响 对于蕴含着固定周期的序列进行步长为 周期长度的差分运算,通常可以较好地 提取周期信息
差分方式的选择 序列蕴含着显著的线性趋势,一阶差分 就可以实现趋势平稳 序列蕴含着曲线趋势,通常低阶(二阶 或三阶)差分就可以提取出曲线趋势的 影响 对于蕴含着固定周期的序列进行步长为 周期长度的差分运算,通常可以较好地 提取周期信息

例5.1 【例1.1】1964年 1999年中国纱年产 量序列蕴含着一个近似线性的递增趋势。 对该序列进行一阶差分运算 Vx,=X,-X-1 考察差分运算对该序列线性趋势信息的提 取作用
例5.1 【例1.1】1964年——1999年中国纱年产 量序列蕴含着一个近似线性的递增趋势。 对该序列进行一阶差分运算 考察差分运算对该序列线性趋势信息的提 取作用 t t t1 x x x

差分前后时序图 原序列时序图 差分后序列时序图 d6 500 0物 400 30 300 200 6名2ae墨 。 10 100 2 -30 0 -40 196019651970197519801985199019952000 196019651970197519801985199019952000 year year
差分前后时序图 原序列时序图 差分后序列时序图

例5.2 尝试提取1950年 1999年北京市民用 车辆拥有量序列的确定性信息 1600 1400 1200 1000 800 NokMHRtm*AeeXK& 600 400 200 0 TTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTT 1950 1960 1970 1980 1990 2000 year
例5.2 尝试提取1950年——1999年北京市民用 车辆拥有量序列的确定性信息

差分后序列时序图 一阶差分 ■于 二阶差分 difl 140 di 130 5 % 30 20 7 10 50 0 -10 30 2 -20 -30 0 -10 -40 1950 1960 19701980 1990 2000 1950 1960 1970 1980 1990 2000 year year
差分后序列时序图 一阶差分 二阶差分
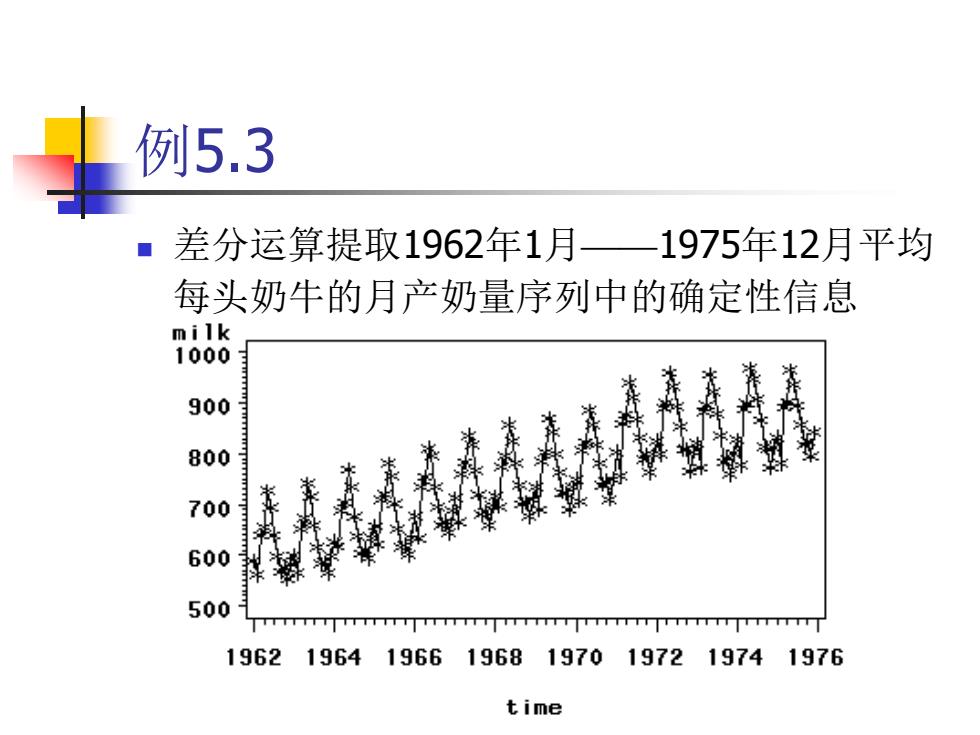
例5.3 ■差分运算提取1962年1月 1975年12月平均 每头奶牛的月产奶量序列中的确定性信息 milk 1000 900 800 700 600 500 1962 1964196619681970197219741976 time
例5.3 差分运算提取1962年1月——1975年12月平均 每头奶牛的月产奶量序列中的确定性信息