
第七章共聚合 7.1引言 7.1.1基本概念 在链式聚合中,由一种单体进行聚合的反应称为均聚合homopolymerization),所得产物 称为均聚物omopolymer)。若两种或两种以上单体共同参与聚合的反应称为共聚合 (copolymeriaion)),产物称为共聚物(copolymer)。共聚物中各种单体的含量称为共聚组成 (copolymer composition)。不同单体在大分子链上的相互连接情况称为序列结构(sequence structure)。在逐步聚合中,将只有一种单体参加的反应称为均缩聚homopolycondensation)。 两种带有不同官能团的单体共同参与的反应称为混缩聚(mixing polycondensation)。在均缩聚 中加入第二单体或在混缩聚中加入第三甚至第四单体进行的缩聚反应称为共缩聚 (co-condensation polymerzation). 7.1.2分类与命名 从不同的角度可将共聚反应和共聚物分成不同的几类。如习惯上将参与共聚的单体种类 数称为“元”,这样可将二种单体参与的共聚反应称为二元共聚,三种单休参与的共聚反应 称为三元共聚、多种单体参与的共聚反应称为多元共聚。从反应历程看,又可分为自由基共 聚、阳离子共聚、阴离子共聚等。目前应用最广的是按序列结构划分。以二元共聚为例,根 据共聚物的链结构,共聚物可分为以下四种主要类型: (1)无规共聚物(random copolymer)。两种单体M1、M在大分子链上无规排列,两单 体在主链上呈随机分布,没有一种单体能在分子链上形城单独的较长链段 ~Mi MiM MM:MiM MiM2 MM 目前研究及工业化的共聚物中多数是这一类,如丁苯橡胶、氯乙烯醋酸乙烯共聚物等。 (2)交替共聚物(alternative copolymer)。两种单体M1、M在大分子链上严格相间排 列。 ~MIMMiM MIMMIM MiM MI 这样的共聚物很少,如苯乙烯马来酸酐共聚物。 (3)嵌段共聚物block copolymer)。由较长的M,链段和较长的M链段间隔排列形城大 分子链。根据链段的多少可以分为二嵌段,如苯乙稀丁二烯共聚物:三嵌段,如苯乙烯丁 二烯-苯乙烯:多嵌段共聚物等。对由M、M两种单体组成的二嵌段共聚物可表示为: ≈一MM1M1MM1M1MM2MMMM2~~ (4)接枝共聚物(grafi 1er)。主链由一种单体组成,支链则由另一种单体组成 MM-M-M2 M-M-M-M-M-M 前三种反应主要是通过两种单体的共聚反应,为本章的主要讨论内容。接枝共聚物一般 是多步反应
共聚物的命名以来源基础命名法和插入一些中介连接字符的方法来表示: (1)以“聚”字开始,继之在括号中共聚合的单体间插入表示共聚方式的中介连接字符, 读法是以“共聚物”为后缀词。如聚(丁二烯-℃0苯乙烯),表示为未定义的共聚物,读作“丁 二烯苯乙烯共聚物”」 (2)将共聚合的单体先用中介符号“.”(或“”)分开,最后加上按共聚合方式相应的 共聚物后缀词,如上例未定义的共聚物写作“丁二烯苯乙烯共聚物”。 表7-1共聚物命名的主要中介连接字符 中介连接字符 含义 法 中介连接字符举例 名称 替恤名 (未定义)共聚 聚(A-o-B) 聚(苯乙烯-o 苯乙烯甲基丙烯酸甲缩 -0- 甲某丙烯酸甲酯) 共聚物 -ran 无规共聚 聚(A-mB】 聚(乙 乙烯乙酸乙酯 乙酸乙烯脂) 交替共聚 聚(苯乙稀-a 马来酸 聚(A-B) 交替共聚 -b(或-bl6k) 段共 聚A-b聚B聚茶乙烯b聚 烯茶乙烯 聚物 8(或g咏-) 接枝共聚聚Ag聚B 聚丁三烯g聚乙烯丁三烯茶乙接枝共聚物 全用小写斜体 *主链(骨干)顺放在名称的首位 无规共聚物命名中,习惯将主单体(含量名的)写在前面,第二单体写在后面。接枝共 聚物是构成主链的单体写在前面,构成支链的单体写在后面。嵌段共聚物习惯上是从大分子 链的一端,按构成大分子链的顺序写。 对多元共聚亦按上述原则处理。若有不同类型的三元共聚,同样要依次用中介连接字符 说明,例如,苯乙稀与丁二烯无规共聚又与丙烯酸乙酯嵌段共聚的三元共聚物,可表示为“聚 (苯乙烯-cr丁二烯)-聚丙烯酸乙酯”。再如“聚A-g聚(B-cC)”表示此接枝共聚物 主链为聚A,支链为B与C的共聚物。 由于共聚物分子式的写法目前还缺少统一规定,写法多样比较混乱,因此对共聚物进 行准确的命名就显得更为重要。 7.1.3研究共聚合的意义 对共聚合的研究,无论在理论上或实际应用上,都具有重要意义。 通过对共聚反应的研究,我们可以测定出单体、自由基、碳阳离子、碳阴离子的相对活 性,进而研究单体结构与反应活性的关系,这在理论研究上有重要意义。 由一种单体合成的均聚物往往由于分子结构上的原因而使制品性能有在某些明显缺陷。 与由多种均聚物通过物理方法形成的共混物不同,参与共聚的各种单体是通过共价键连接在 一根大分子裤上的。这样可以更有效地收变大分子链的结构,讲而收讲聚合物的性能。如收 进机械强度、弹性、塑性、柔软性、玻璃化温度、塑化温度、熔点、溶解性能、染色性能、 表面性能等。性能改变的程度与参与共聚的单体种类、共聚组成、序列结构有关。表7-2是 典型共聚物改性的例子

表7-2典型共聚物 主单体 节一消水 改讲的性能及主要用途 乙烯 酷酸乙酯 增加柔性,软塑料:可供作聚氯乙烯共混料 丙 破坏结品性,增加柔性和弹性:乙丙橡 异丁烯 异戊二 引入双键,供交联用:丁基橡胶 “一 增加强度:通用橡胶 ”一 丙烯咭 增加油性:丁晴橡胶 苯乙烯 丙烯 提高抗冲强度:增韧塑料 氯乙烯 酸乙烯酯 增加塑性和溶解性能:料和涂料 加每了塔 破坏结构规整性,增柔性:特种橡胶 甲基丙烯酸甲酯 苯烯 改菩流动性能和咖工性能:塑料 丙烯密 丙烯酸甲酯衣块酸 改普柔软性和染色性能:合成纤维 马老酸 醋酸乙烯酯或苯乙烯改进聚合性能:用作分散剂和织物处理剂 通过共聚合,可以使有限的单休通过不同的组合得到多种多样的聚合物,满足人们的名 种需要。如聚苯乙烯为一种通用塑料,聚丁二烯为一种通用橡胶,二种单体无规共聚,产物 为目前产量最大的合成橡胶,即丁苯橡胶(SBR):如嵌段共聚,产物为一种热塑性弹性体SBS): 如接枝共聚产物为高抗中聚茶乙烯PS)。又如聚氯乙烯为一种脆性材料,日存在抗老化差, 热成型变色的问题。如与5%的醋酸乙烯酯共聚,增加了柔性,可用于制管、薄板:当醋酸乙 烯酯含量占到50%,产品可用于制人造革:如与40%的丙烯睛共聚,产物的耐油性、耐溶性增 加,可用于过滤材料:与乙烯或丙烯共聚,提高了热稳定性,可用于无毒包装材料,与偏 氯乙烯共聚,可提高气密性,用于包装薄膜。尤其是有些化合物如马来酸酐本身不能用作单 体进行均聚,但可通过加入第二种单体如苯乙烯或醋酸乙烯酯进行共聚。这就扩大了合成聚 合物的原料范围。高分子科学发展到今天,大路通用单体已基本实现了工业化生产,共聚合 就更品示出重要意义。 在均聚反应中,聚合机理、聚合反应速率、平均相对分子质量及相对分子质量分布是研 究的重要内容,在共聚合中,单体参与共聚的能力、共聚组成和序列结构是研究的主要内容。 本章主要讨论由两种单体参与的链式共聚合反应。 7.2共聚物的组成 共聚物组成(copolymer composition)是指共聚物中含参加共聚各单体所占的比例,是决 定共聚物性能的主要因素之一。要得到顶期共聚物组成的共聚物不是一件容易做到的事,首 先是由于共聚中两种链活性中心对两种单体的反应活性各不相同的缘故,在共聚合时共聚物 的组成与单体配料组成往往相差甚大:其次在反应过程中活性大的单体消耗得快,随反应的 进行,体系中单体组成也在不断地变化,这样在不同反应阶段形成的共聚物的共聚物组成也 为一个变值,即在每一瞬间形成的共聚物的瞬时组成是各不相同的,当然整个共聚物的共聚 组成也是不均匀的。为此,需要对共聚物组成与单体组成间关系的基本规律进行研究。 7.2.1共聚物组成方程 共聚物组成方程描述的是共聚物组成与单体组成之间的定量关系,这种关系可由共聚反 2

应动力学或链增长的几率幸推导出来。1944年Mayo和Lewis分析了二元共聚反应,由反应动 力学出发推导出共聚物组成方程,奠定了共聚反应的理论基础。 现以自由基二元共聚为例,由动力学出发进行共聚物组成方程(Mayo-Lewis式)的推导。 共聚反应的基元反应数目比均聚反应要多得多,如n元共聚,最少要有n个引发反应, n2个链增长反应和+1)2个双基终止反应。如加上各种链转移反应,总的基元反应还要多。 为简化研究,设共聚反应只有正向进行的链引发反应、链增长反应和链终止反应。反向进行 的解聚反应对均聚来说,只会影响均聚物的相对分子质量,谈不上组成问题,但对共聚反应 而言,则有可能导致共聚组成的改变,因此设体系中没有解聚反应。 以M和M代表两种参加共聚的单体,则链引发反应式为: R·+M1+RM1· R·+M→RM 对链增长反应,设无前末端效应:链自由基前末端(倒数第二个)单体单元对自由基的 活性没有影响,即自由基活性仅取决于末端单元的结构。这样共有四个链增长反应。同时设 自由基活性与链长无关,即等活性假设。以~~M·和~~M·分别代表两种链自由基。 k1、k2、k22、k1为相应的链增长反应速率常数,下标中第一个数字表示增长自由基中末端 单体单元种类,即自由基的种类,第二个数字表示与之反应的单体种类。则链增长反应式为: M+MM Ru=kuIMI[M1 (7-1) ~~M+M R2=k2M1·M2 (7-2) M·+M )M· Rn=kM·1Ml (7-2) -M2+Mi -Mi Ra1=kM·]M (7-4) 式中[M·]和M]分别代表末端为M的链自由基和单体M的浓度,余类准。 对正常的双基终止反应而言,反应式为: 一M·+·M一~一·死的大分子 一M。+·M ·死的大分子 -M2·+·2 ·死的大分与 设共聚物相对分子质量很大,单体基本消耗在链增长反应一步,则引发反应和终止反应 对共聚物组成没有能响,两种单体的消失速率或进入共聚物的速率仅取决于链增长反应速率, _d[M ]-+-k [M,J[M.]+ka[M:][M] (7-5) dt _d[M:]-R+R=k[M.J[M:]+kz[M:JM:] (7-6) dt 两种单体的消耗速率比等于两种单体进入共聚物的速率比,也就是共聚物的组成: dM_knMM]+kM,M (7-7) d[M:k2[M,][M:]+k2[M:][M: 7-7式中含有两种自由基浓度,无法直接使用。与推导自由基聚合动力学方程一样,在 这里需要对两种活性中心分别作稳态假定,即要求体系中自由基总浓度和两种自由基的浓度 都不变。这一假定包含二个方面:一是M·和M·的引发速率分别等于各自的终止速率: 另一个是它们之间相互转换的速率必需相等。对反应式7-1和7-3来说,由于为两种单体的 均聚反应,对活性中心数目没有影响。要保证上述假定成立,必须有反应式7-2和7-4的速

率相等,即: kM·]M]-k2M·][M] (7-8) 代入式7-7,得: dM]_[M】.(kk2)M]+[M,] (7-9) d[M,[M:(k2/k2)[M:]+[M] 定义参数上和r为: 6安 (7-10) 参数r和r:称作单体竞聚率(reactivity ratio),为单体均聚和共聚链增长反应速率之比, 表征两单体进行共聚的相对活性大小。代入式79得: d[M [M:][M,]+[M: (7-11) dM:】[M2]rM2]+[M] 式7-11是以两单体的摩尔比或浓度比来描述共聚反应某一瞬间所形成共聚物的组成与 该瞬间体系中单体组成的定量关系,称为以摩尔比(或浓度比)表示的共聚物组成微分方程。 通过链增长反应的几率,也可得到同样的结果。 习惯上,常采用摩尔分数代替摩尔比或浓度比来表达共聚组成方程。 令、:分别代表某瞬间单体M、M占单体混合物的摩尔分率,即: [M] f=1-6,=M1+M (7-12) 令F、F2分别代表同一瞬间单体M、M占共聚物的摩尔分率,即: E=1-F2= d(M,] (7-13) d[M ]+d[M, 将式7-11和7-12代入式7-10,得: nf2+ff 写=f+2f+, (7-14) 式7-14是以两单体的摩尔分率或浓度分率来描述共聚反应某一瞬间所形城共聚物的组成与 该瞬间体系中单体组成的定量关系,称为以摩尔分率(或浓度分率)表示的共聚物组成微分 方程。具有 以重量分率表示的共聚物组成方程为: (7-15) X= x 式中X,为某瞬间所形成的共聚物中M链节的重量分数 5

x为未反应单体中M的重量分率 K为MM,代表两单体的相对分子质量之比 类似地也可以表示为以重量比或重量分率表示的共聚组成微分方程。在不同的场合,可 根据具体情况选用不同的方程。 归纳起来,在以动力学方法推导共聚物组成议程时曾作了下面几个假定: ①不考虑解聚反应,设聚合反应为正向的不可逆反应: ②不考虑前末端效应,链自由基一端倒数第二个单元对自由基活性无影响: ③等活性假定,自由基活性与链长无关: ④聚合度很大,引发和终止反应对共聚物组成没有影响: ⑤稳态假定,体系中自由基总浓度和两种自由基的浓度都不变,即要求引发速率和 终止速率相等,同时两种自由基相互转化的速度相等。 对于多数自由基二元共聚而言,上述假定均可成立。一些超出此范围的情况将在后面给 予讨论。对于离子型二元共聚,在多数情况下上述公式依然成立。 7.2.2共聚物组成曲线 式7一11反映了共聚反应某一瞬间所形成共聚物的组成与这一瞬间体系单体组成之间关 系。可以看出影响共聚组成的主要因素是两种单体浓度及它们的竞聚率。 在二元共聚反应中,活性中心~~M·可同时与两种不同的单体反应,即有在一对相互 竞争的链增长反应: M1→MM1· ~一M1·+ M→一MM· 对单体M的竞聚率定义为:互=L,标征~M·链自由基同自身单体M进行自聚的反 k 应能力与同异种单体M进行共聚的反应能力之比。反过来看,也就是两种单体与同一种链 自由基反应的相对活性。从单体的角度看,竞聚率反映了竞争聚合时两种单体反应活性的比 较:从聚合的角度看,竞聚率反映了链自由基进行自聚与共聚的能力比较。因此竞聚率是判 断单体活性和共聚行为的重要参数。 当n>1,即k>k12时,表明链自由基~~M·易和自身单体M反应而不易和异种 单体M反应。易自聚而不易共聚,或均聚倾向大于共聚倾向。 当n<1,即k1<k2时,表明链自由基~~M·易和异种单体M反应而不易和自身 单体M反应。易共聚而不易自聚,或共聚倾向大于自聚倾向。 当=1,即k1=k2时,表明链自由基~M·和两种单体M、M反应的活性相同 发生均聚和发生共聚的几率相等。 当1=0,即k1=0,k2≠0时,表明链自由基~~M·只能和异种单体M反应而不能 和自身单体M,反应。即只能共聚而不能自聚。 当r,=∞,即k11≠0,k2≈0时,表明链自由基一一M·只能和同种单体M1反应而不 能和异种单体M反应,即只能自聚而不能共聚。在实际中尚未发现这种情祝。 对:也可进行类似的分析。 式7-14表明共聚组成F是单体组成的函数。当竞聚率确定后,对于一系列不同的单 6
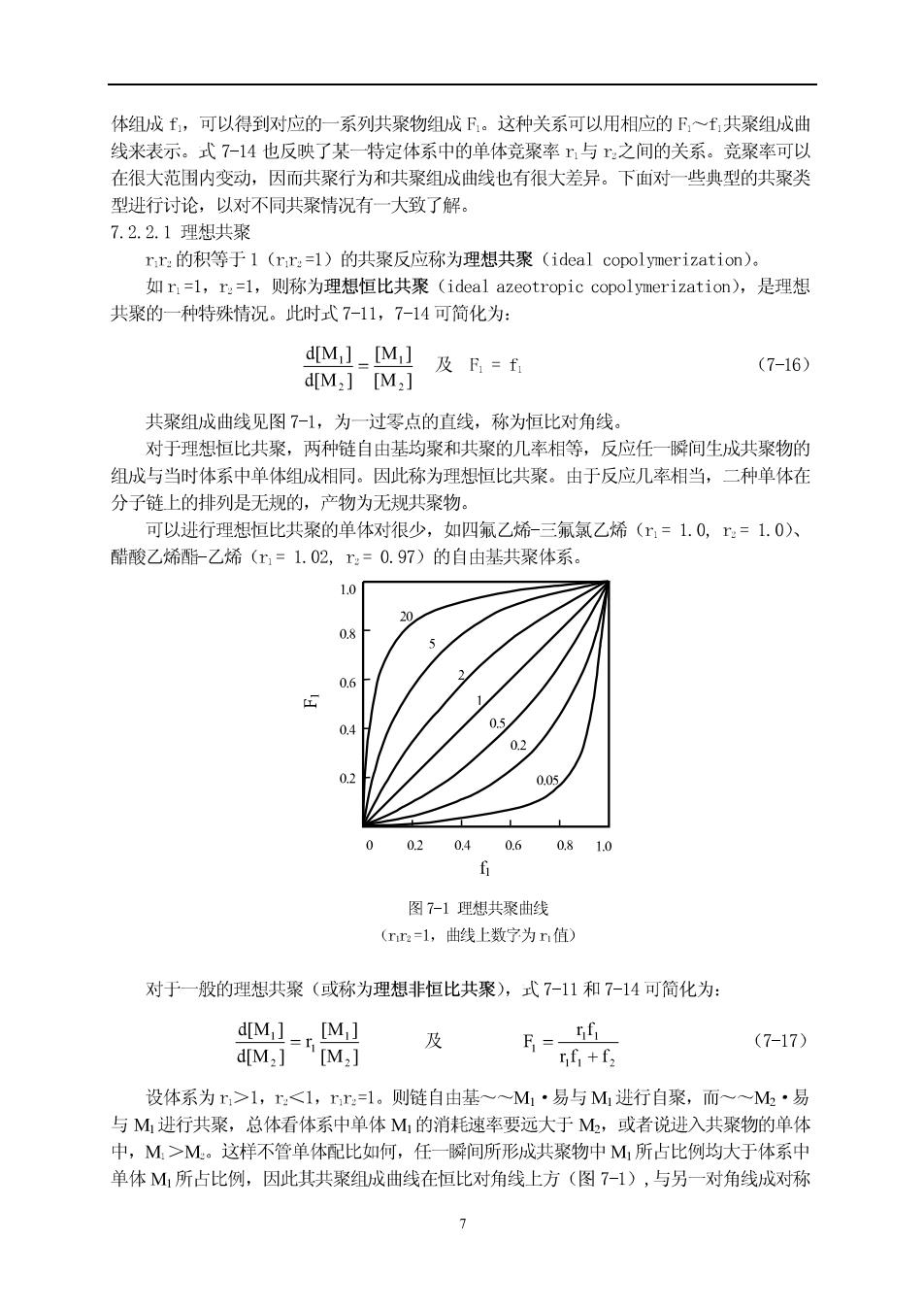
体组成f,可以得到对应的一系列共聚物组成F。这种关系可以用相应的F~共聚组成曲 线来表示。式7-14也反映了某一特定体系中的单体竞聚率与之间的关系。竞聚率可以 在很大范制内变动,因而共聚行为和共聚组成曲线也有很大差异。下由对一些典型的共聚类 型进行讨论,以对不同共聚情况有一大致了解。 7.2.2.1理想共聚 rr:的积等于1(rr=l)的共聚反应称为理想共聚(ideal copolymerization)。 如r=l,r=l,则称为理想恒比共聚(ideal azeotropic copolymerization),是理想 共聚的一种特殊情况。此时式7-11,7-14可简化为: dM1-M及B=E (7-16) dM2][M,】 共聚组成曲线见图7-1,为一过零点的直线,称为恒比对角线。 对于理想恒比共聚,两种链自由基均聚和共聚的几率相等,反应任一瞬间生成共聚物的 组成与当时体系中单体组成相同。因此称为理想恒比共聚。由于反应几率相当,二种单体在 分子链上的排列是无规的,产物为无规共聚物。 可以进行理想恒比共聚的单体对很少,如四氟乙烯-三氟氯乙烯(=1.0,r=1.0)、 醋酸乙烯酯乙烯(x=1.02,x=0.97)的自由基共聚体系。 1.0 05 0 0204 0.6081.0 图7-1理想共聚曲线 (rr2=l,曲线上数宁为r,值】 对于一般的理想共聚(或称为理想非恒比共聚),式7-11和7-14可简化为: 及 E,+ t (7-17) 设体系为>1,rM。这样不管单体配比如何,任一瞬间所形成共聚物中M所占比例均大于体系中 单体M所占比例,因此其共求组成曲线在恒比对角线上方(图7-1),与另一对角线设对际 7

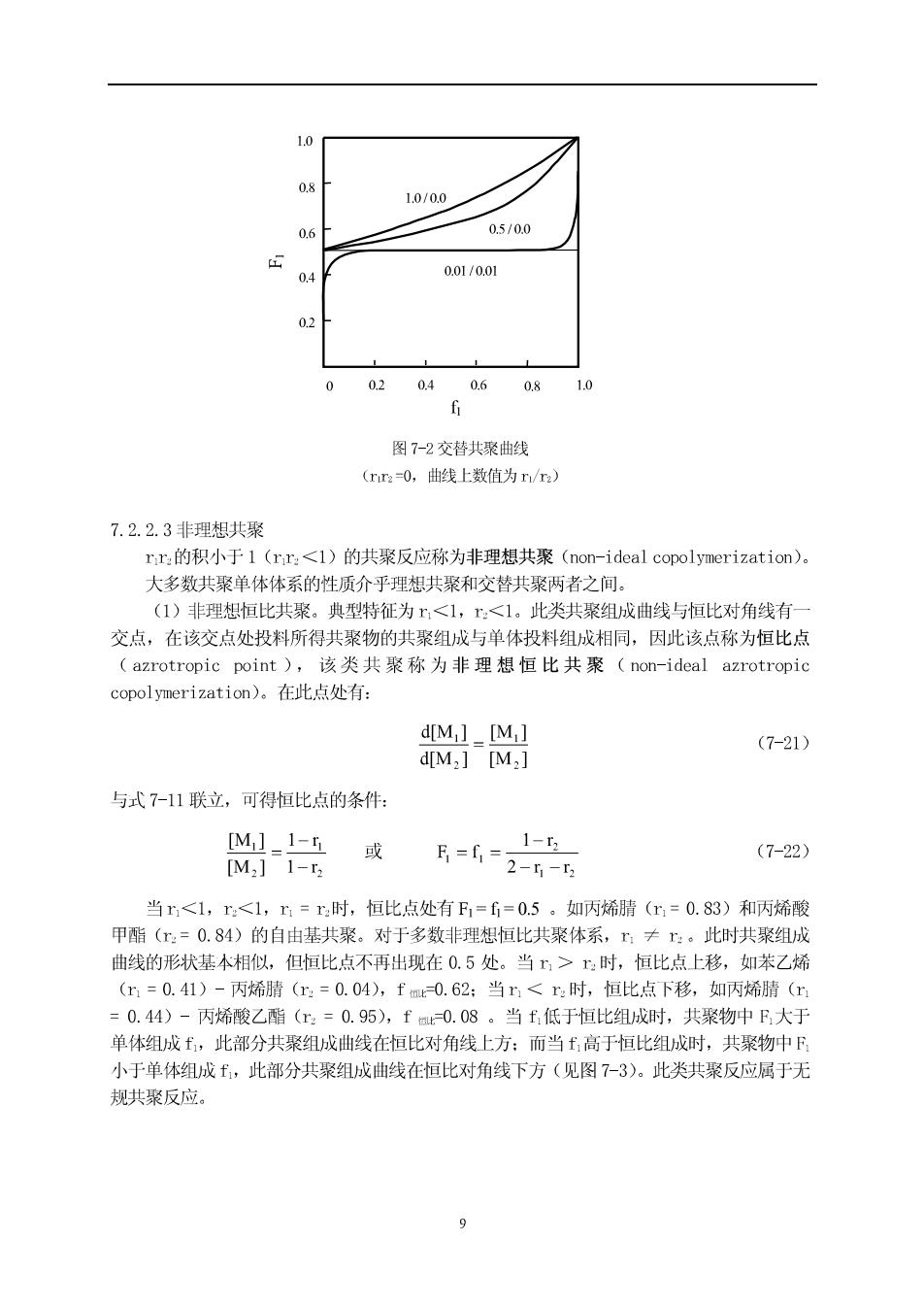
状况,且r值越大,共聚组成曲线距恒比对角线越远。对1,r,=1的体系,可 作相同的分析,不过这时的共聚组成曲线在恒比对角线的下方(图7-1) 理想共聚概念的提出借用了理想液体混合物中的气液平衡特性,并不是说这类共聚反应 在任何意义上都是最理想的。理想共聚的一个极其重要、具有实际意义的结论是随着两种单 体竞聚率差别的增大,要合成两种单体含量都较高的共聚物就越困难。在:=1的条件下: KiK2L (7-18 k12 k22 说明两种单体结合到共聚物上的相对速率与链自由基种类无关,为无规共聚,共聚物中两单 体单元摩尔比是体系中两单体摩尔比的,倍。当两单体的竞聚率相差过大时,就得不到含有 大量单体M的共聚物。如=10,n0.1,即使投料时M的摩尔含量为80%,所得共聚物 中M的单元结构的摩尔含量仅为18.5%。只有当和r:没有显著差别时(如r0.5~2), 才会在很大的共聚单体投料组成的范围内得到两种单体含量都较多的共聚物。 60℃时丁二烯(m=1.39)-苯乙烯(=0.78)、偏二氯乙烯(=3.2)-氯乙烯 (=0.3)的自由基共聚体系接近理想共聚。大多数离子型共聚(包括阳离子共聚和阴离子 共聚),具有理想共聚的特征。 7.2.2.2交替共聚 交替共聚的典型特征为rr=0 对于两种单休的竞聚率均为零或均趋于零的体系,两种链自由基都不能和自身单体进行 均聚而只能与异种单体进行共聚,所形成共聚中两种单体单元严格交替排列。不论单体投 单体投料配比如何,当含量少的单体消耗光后聚合反应不再进行,剩下末反应的含量多的单 体,即共聚组成与单体组成、转化率无关。 式7-11和7-14可简化为: (7-19) 共聚组成曲线见图7-2,为一条水平线。 能够进行自由基交替共聚的体系不多,如马米酸酐和乙酸2氯烯丙基酯、异丁烯和反丁 烯二酯二乙酯。离子型共聚由于取代基极性效应的影响,交替共聚的倾向要比自由基共聚小 如m>0,=0,则式7-11为 瑞1 (7-20) 单体M的一定的自聚能力,M则只能共聚而不能均聚。当较小、M过量较多时,产物 基本为交替共聚物。如两种单体的活性相差不多,则共聚物中F>50%。60℃苯乙烯(r=0.01) 和马来酸酐(=0)自由基共聚就是这方面的例子
1.0/00 0510.0 0.01/0.01 02 04 0.6 0.8 图7-2交替共聚曲线 (nn-0,曲线上数值为n/m) 7.2.2.3非理想共聚 rr的积小于1(rr:时,恒比点上移,如苯乙烯 (11=0.41)-丙烯腈(12=0.04),fm0.62:当r<时,恒比点下移,如丙烯腈(r =0.44)-丙烯酸乙酯(:=0.95),fa0.08。当低于恒比组成时,共聚物中B大于 单体组成,此部分共聚组成曲线在恒比对角线上方:而当高于恒比组成时,共聚物中F 小于单体组成,此部分共聚组成曲线在恒比对角线下方(见图7-3)。此类共聚反应属于无 规共聚反应
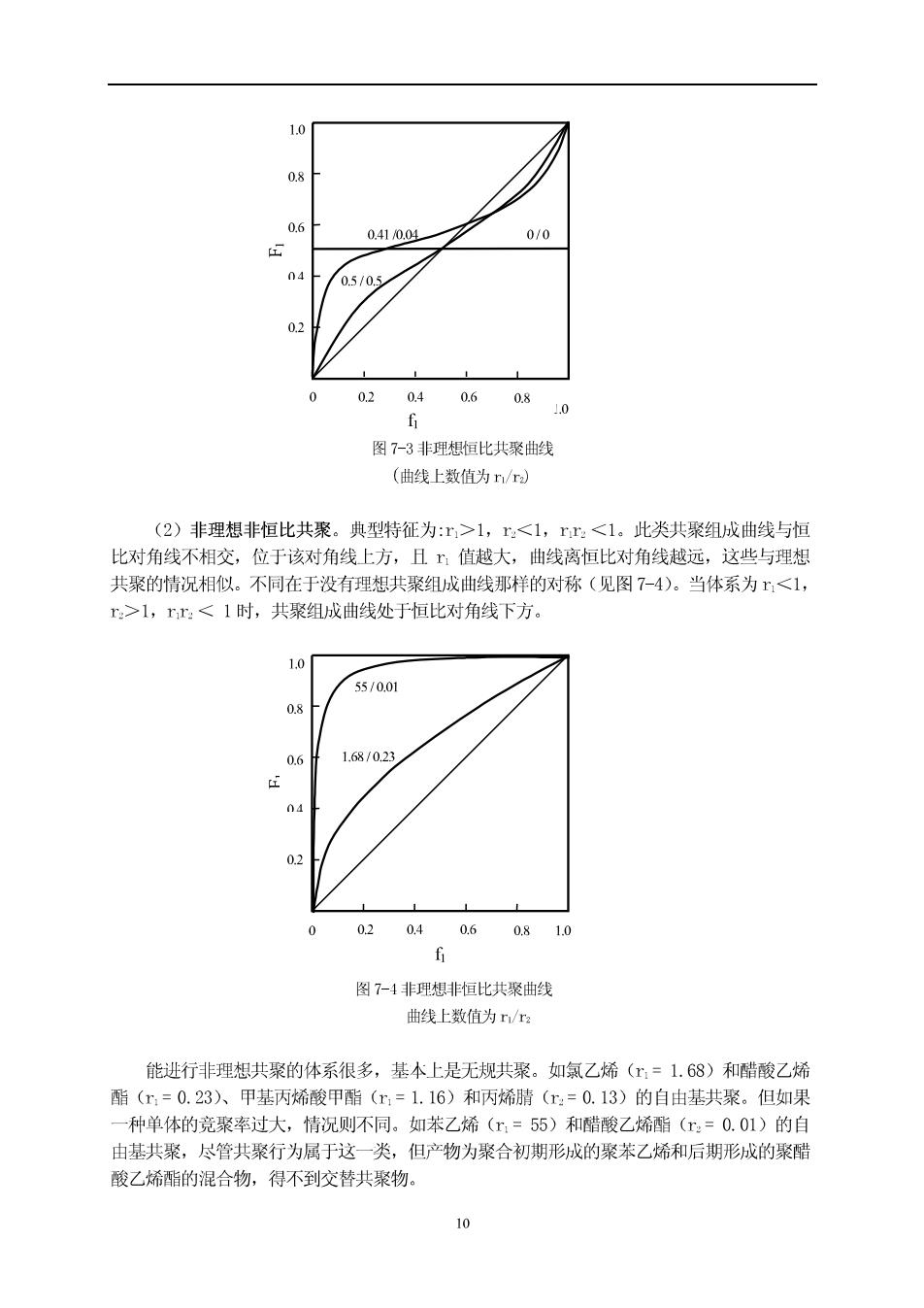
0.41004 0/0 0 0.5/0s 02 040.608 1.0 f 图7-3非理想恒比共聚曲线 (曲线上数值为r/r) (2)非理想非恒比共聚。典型特征为:r>1,1,rr<1时,共聚组成曲线处于恒比对角线下方。 1.01 55/001 1.68/023 0 0204 0.6 0.810 6 图?-4非理想非恒比共聚曲线 曲线上数值为n/ 能进行非理想共聚的体系很多,基本上是无规共聚。如氯乙烯(=1.68)和醋酸乙烯 酯(m=0.23)入、甲基丙烯酸甲酯(m=1.16)和丙烯腈(r:=0.13)的自由基共聚。但如果 一种单体的竟聚率过大,情况则不同。如苯乙烯(m=55)和醋酸乙烯酯(x=0.01)的自 由基共聚,尽管共聚行为属于这一类,但产物为聚合初期形成的聚苯乙烯和后期形成的聚醋 酸乙烯酯的混合物,得不到交替共聚物