
调查问卷的统计分析讲义 §1调查问卷的信度 1.1信度的含义 一个良好的教有测验首先必须保证测验的结果可靠,测验结果的可靠性程度称为测验的 信度,简单的说就是测量结果的可信程度,记为 每次的测量结果实际包含被测的实际水平和测量误差两部分。 物理测量:皮尺、钢尺、台秤、天平: 教有和心理测量:各种测验量表: ·产生随机误差的因素:施测环境、读数、时间、主被试关系、被试的动机和情绪等 如果用同一测量工具反复测量同一种特质对象,则多次测量结果间的一致性程度就叫信 度。测量的一致性程度越高说明测量结果越稳定,由此人们在使用所得测值时就会感觉其可 靠性越高。 测验信度是对测验工具及其操作的整体质量的一种量度,是测验性能的重要质量指标。 信度高是良好测验的必要条件,但不是充分条件。一个测验只具有可靠性还不行,还必 须具备有效性。 1.2信度的计算 在教有测量学中对信度的估计或计算,一般采用相关分析的方法,即计算出两种变量的 相关系数 (例如:计算两次测验同一对象的分数的相关系数),用相关系数的大小来表 示一致性程度的高低。可根据测试结果分数的形式,是连续变量还是二分变量等,可采用不 司的相关系数计算公式。 根据信度计算的不同方法,可将信度分为重测信度、复本信度、同质性信度、评分者信 度。 1.重测信度 指用同一量表(测验或评价表)对同一组被试施测两次所得结果的一致性程度。其大小 等于同一组被试在两次测验上所得分数的相关系数。 重测信度的基本假设:假设某测验所要测量的潜在特质,短期内不会随时间推移而 改变。故重测信度的高低和测量时间间隔长短密切相关。 间隔多久恰当呢?无固定标准,一般来说,在间隔时间内,被试的遗忘和练习的效果 基本上相互抵消,即为适度的时间间隔。 *适用于速度测验而不适应于难度测验的信度估计 女重测信度检验测验跨时间的稳定性。 *注意提高被试的积极性。 例1:用某量表测验10名学生,得分记为X,为考察测量结果的可靠性,于16天后用原量 表对这10名同学再测一次,得分记为Y,问测验结果是否可靠? 学生 X Y A 88 94 8272 7744 8836 B 80 78 6240 6400 6084 c 68 56 3808 4624 3136
调查问卷的统计分析讲义 §1 调查问卷的信度 1.1 信度的含义 一个良好的教育测验首先必须保证测验的结果可靠,测验结果的可靠性程度称为测验的 信度,简单的说就是测量结果的可信程度,记为 。 每次的测量结果实际包含被测的实际水平和测量误差两部分。 •物理测量:皮尺、钢尺、台秤、天平; •教育和心理测量:各种测验量表; •产生随机误差的因素:施测环境、读数、时间、主被试关系、被试的动机和情绪等; 如果用同一测量工具反复测量同一种特质对象,则多次测量结果间的一致性程度就叫信 度。测量的一致性程度越高说明测量结果越稳定,由此人们在使用所得测值时就会感觉其可 靠性越高。 测验信度是对测验工具及其操作的整体质量的一种量度,是测验性能的重要质量指标。 信度高是良好测验的必要条件,但不是充分条件。一个测验只具有可靠性还不行,还必 须具备有效性。 1.2 信度的计算 在教育测量学中对信度的估计或计算,一般采用相关分析的方法,即计算出两种变量的 相关系数 (例如:计算两次测验同一对象的分数的相关系数),用相关系数的大小来表 示一致性程度的高低。可根据测试结果分数的形式,是连续变量还是二分变量等,可采用不 同的相关系数计算公式。 根据信度计算的不同方法,可将信度分为重测信度、复本信度、同质性信度、评分者信 度。 l.重测信度 指用同一量表(测验或评价表)对同一组被试施测两次所得结果的一致性程度。其大小 等于同一组被试在两次测验上所得分数的相关系数。 重测信度的基本假设:假设某测验所要测量的潜在特质,短期内不会 随时间推移而 改变。故重测信度的高低和测量时间间隔长短密切相关。 间隔多久恰当呢?无固定标准,一般来说,在间隔时间内,被试的遗忘和练习的效果 基本上相互抵消,即为适度的时间间隔。 *适用于速度测验而不适应于难度测验的信度估计。 *重测信度检验测验跨时间的稳定性。 *注意提高被试的积极性。 例 1:用某量表测验 10 名学生,得分记为 X,为考察测量结果的可靠性,于 16 天后用原量 表对这 10 名同学再测一次,得分记为 Y,问测验结果是否可靠? C 68 56 3808 4624 3136 B 80 78 6240 6400 6084 A 88 94 8272 7744 8836 学生 X Y X·Y X2 Y2

重测信度的计算 本例采用积差相关系数公式 N∑XW-∑x∑Y Vw∑-区xwΣr-②y旷 10×46742-659×676 。10x4749-659i0x48256-676 X为第一次测验的实得分数;Y为第二次测验的实得分数;N为被试人数。 计算得rx=0.68,显著性水平取0.05 查积差相关系数检验表得r0.0s(8)=0.632,rxx>raos(8), 说明两次测验所得分数显著相关,故该测验信度高,测验结果可靠,作出此结论的可靠度为95% 思考一下: 若测量结果不是以分数的形式给出,而是等级排列或二分变量时如何求取重测信度? 积差相关公式的运用条件: 两个变量连续,且成线形关系 ·数据成对 ·两个变量的总体呈正态分布或至少为单峰对称分布 ·数据的对数最好在30对以上
重测信度的计算: 本例采用积差相关系数公式 X 为第一次测验的实得分数;Y 为第二次测验的实得分数;N 为被试人数。 计算得 rxx=0.68, 显著性水平取 0.05, 查积差相关系数检验表得 r0.05(8)=0.632, rxx>r0.05(8) , 说明两次测验所得分数显著相关,故该测验信度高,测验结果可靠,作出此结论的可靠度为 95% 思考一下: 若测量结果不是以分数的形式给出,而是等级排列或二分变量时如何求取重测信度? 积差相关公式的运用条件: •两个变量连续,且成线形关系 •数据成对 •两个变量的总体呈正态分布或至少为单峰对称分布 •数据的对数最好在 30 对以上 ( ) ( ) − − − = 2 2 2 2 N X X N Y Y N XY X Y rxx ( ) ( ) 2 2 10 47449 659 10 48256 676 10 46742 659 676 − − − rxx =
那么,当以上条件不满足时,如何处理? ·复本信度 有些测验不适合施测两次,这时我们可以编制两份等值但并不相同的量表对被试施测 (其时距尽量短,可短到两次测验接着进行),两个平行测验测量同一批被试所得结果的一致 性程度称为复本信度,其大小等于同一批被试在两个复本测验上所得分数的相关系数。 所谓测验的等值(或平行)是指: &试题题型、题数、难度、指导语说明、施测要求等方面都相当 &用来测量相同潜在特质或属性 &试题不相同。 两种方式:同一时间连续施测:间隔一段较短的时间后施测。 例2:假设对10名学生用两个等值的测验A、B施测,测验实得分数分别用X和Y表示,测 验结果如下:求该测验的信度? XIA) Y(B) X.Y X2 Y2 1 74 76 5624 5476 5776 2 71 75 5325 5041 5625 3 72 71 5112 5184 5041 68 70 4760 4624 4900 5 76 76 5776 5776 5776 6 73 79 5767 5329 6241 7 67 65 4355 4489 4225 8 70 77 5390 4900 5929 9 65 62 4030 4225 3844 10 74 72 5328 5476 5184 710 723 51467 5052052541 本例仍利用积差相关系数计算复本信度。 N∑Y-∑X∑y “3x-区x对2-②列
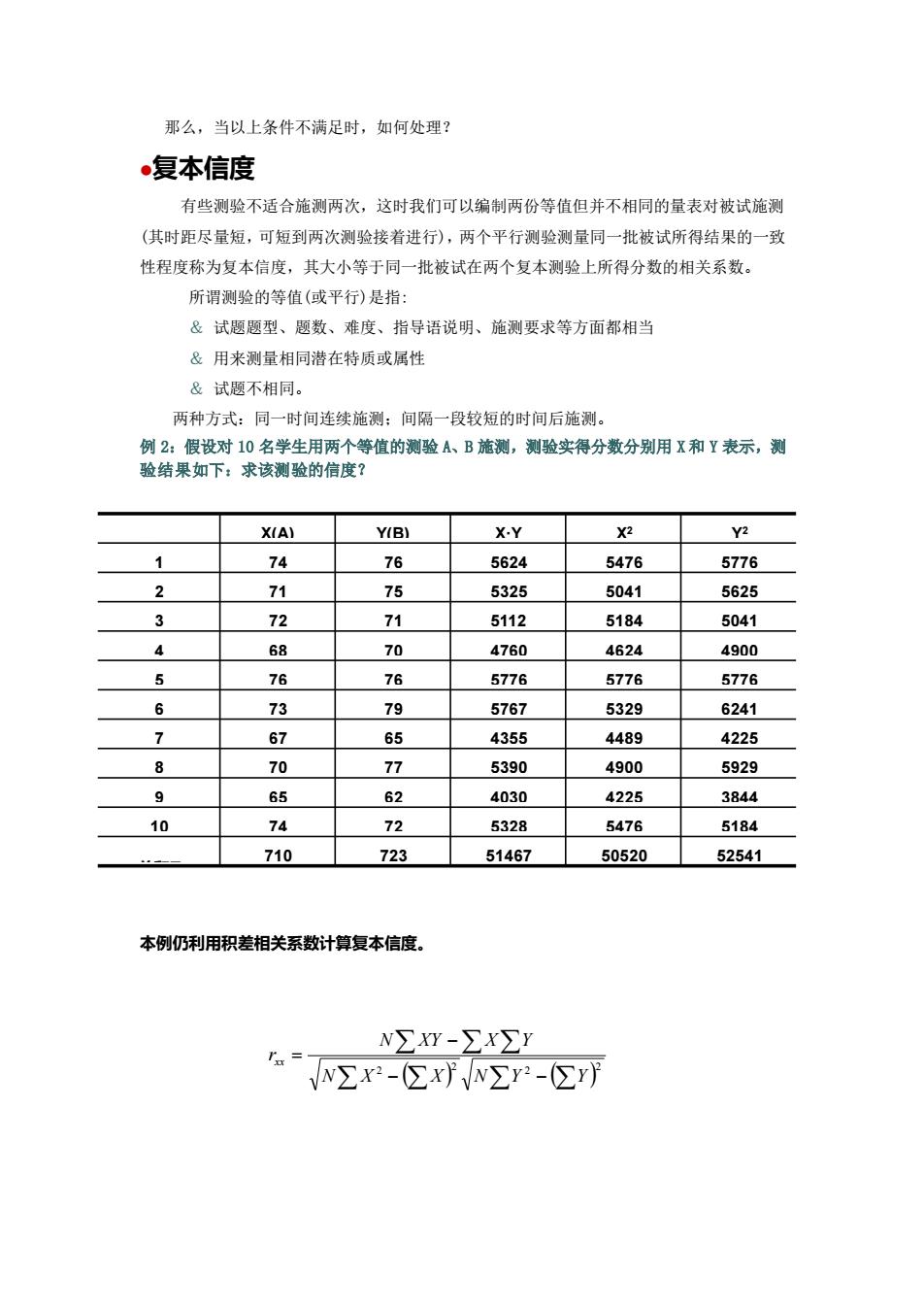
那么,当以上条件不满足时,如何处理? ⚫复本信度 有些测验不适合施测两次,这时我们可以编制两份等值但并不相同的量表对被试施测 (其时距尽量短,可短到两次测验接着进行),两个平行测验测量同一批被试所得结果的一致 性程度称为复本信度,其大小等于同一批被试在两个复本测验上所得分数的相关系数。 所谓测验的等值(或平行)是指: & 试题题型、题数、难度、指导语说明、施测要求等方面都相当 & 用来测量相同潜在特质或属性 & 试题不相同。 两种方式:同一时间连续施测;间隔一段较短的时间后施测。 例 2:假设对 10 名学生用两个等值的测验 A、B 施测,测验实得分数分别用 X 和 Y 表示,测 验结果如下:求该测验的信度? 本例仍利用积差相关系数计算复本信度。 10 74 72 5328 5476 5184 710 723 51467 50520 52541 总和∑ 9 65 62 4030 4225 3844 8 70 77 5390 4900 5929 7 67 65 4355 4489 4225 6 73 79 5767 5329 6241 5 76 76 5776 5776 5776 4 68 70 4760 4624 4900 3 72 71 5112 5184 5041 2 71 75 5325 5041 5625 1 74 76 5624 5476 5776 X(A) Y(B) X·Y X2 Y2 学生 ( ) ( ) − − − = 2 2 2 2 N X X N Y Y N XY X Y rxx

10×51467-710×723 Fo=- 10×50520-(710V10×52541-(723} 计算得rx=0.78,显若性水平取0.01 查积差相关系数检验表得r0.01(8)=0.765,ra>r0.01(8), 说明两测验所得分数显著相关,故测验信度高,测验结果可靠,作出此结论的可靠度为99%】 重测信度和复本信度在使用的方法上分别属于跨时间和跨类型的 实际操作中存在困 难,均需测验两次,复本不易做到等值,很难用同一测验对同一组被试重复进行测验等,于 是引入内部一致性信度来计算测验的信度。 ·内部一致性信度 也叫同质性信度,是指测验内部所有题目间的一致性程度。题目间的一致性含有两层 意思:其一是指所有题目测的是同一种心理特质:其二是指所有题目得分 之间都具有较高的 正相关。 同质性信度基于的假设是:当一个测验具有较高的同质性信度时,说明测验主要测的 是某一单个心理特质,由于众多的题目测试了同一心理特质,那么实测结果就是该特质水平 的反映。 估计同质性信度的方法主要有:分半信度、库德一理查逊信度、克龙巴赫α系数、益 伊特信度 (1)分半信度 指的是将一个测脸分成对等的两半后,所有被试在这两半上所得分数的一致性程度。 计算不难,抑对等的两半测验看成是在最短时间距离内施测的两个平行测验。难的是, 如何将测验分成相等的两半 按题号的奇偶分半、按题目的难易程度分半、按题目的内容分半等等。 实际应用中,由于题目一般依据难度大小排列,采用奇偶分半可使两半测验的题目在 难度上基本相等,因此常被采纳。 如果一个测验无法分成对等的两半,则不宜使用分半信度。 由于分半信计算的是两个“半测验”上得分的相关系数,只是半个测验的信度,(测验越 长信度越高),因此必须用斯皮尔曼-布朗公式加以校正: n=2r/+h)) 式中,r为整个测验的信度系数,为两个“半测验”上得分的相关系数 例:15名被试在奇偶分半测明验上的得分
计算得 rxx=0.78, 显著性水平取 0.01, 查积差相关系数检验表得 r0.01(8)=0.765, rxx>r0.01(8) , 说明两测验所得分数显著相关,故测验信度高,测验结果可靠,作出此结论的可靠度为 99%。 重测信度和复本信度在使用的方法上分别属于跨时间和跨类型的,实际操作中存在困 难,均需测验两次,复本不易做到等值,很难用同一测验对同一组被试重复进行测验等,于 是引入内部一致性信度来计算测验的信度。 •内部一致性信度 也叫同质性信度,是指测验内部所有题目间的一致性程度。题目间的一致性含有两层 意思:其一是指所有题目测的是同一种心理特质;其二是指所有题目得分之间都具有较高的 正相关。 同质性信度基于的假设是:当一个测验具有较高的同质性信度时,说明测验主要测的 是某一单个心理特质,由于众多的题目测试了同一心理特质,那么实测结果就是该特质水平 的反映。 估计同质性信度的方法主要有:分半信度、库德-理查逊信度、克龙巴赫α系数、荷 伊特信度。 (1)分半信度 指的是将一个测验分成对等的两半后,所有被试在这两半上所得分数的一致性程度。 计算不难,把对等的两半测验看成是在最短时间距离内施测的两个平行测验。难的是, 如何将测验分成相等的两半。 按题号的奇偶分半、按题目的 难易程度分半、按题目的内容分半等等。 实际应用中,由于题目一般依据难度大小排列,采用奇偶分半可使两半测验的题目在 难度上基本相等,因此常被采纳。 如果一个测验无法分成对等的两半,则不宜使用分半信度。 由于分半信计算的是两个“半测验”上得分的相关系数,只是半个测验的信度,(测验越 长信度越高),因此必须用斯皮尔曼-布朗公式加以校正: 式中,rxx 为整个测验的信度系数,rhh为两个“半测验”上得分的相关系数。 例: 15 名被试在奇偶分半测验上的得分 ( ) ( ) 2 2 10 50520 710 10 52541 723 10 51467 710 723 − − − rxx = ( ) xx hh hh r = 2r 1+ r

.0020005060708091011213141 =2182217182017161314131288 -2221218151417151614121076 计算两个“半测验”得分的积差相关系数为:0.86。代入公式得: r=2h/1+h)=(2×0.86)/0+0.86)=0.92 由于斯皮尔曼-布朗公式有个基本假设,即:两个半测验”满足方差齐性,故,当数据 资料不能满足这一假设时,应选择下述两个等价的公式之一 ④弗朗那根(Flanagan)公式 .=2-(S+s/s] 式中,S。,?和S,2分别表示所有被试在两半测验上得分的方差;S表示所有被试在整 测验上的总得分的方差。 ②卢仑(Rulon)公式 ro =1-Si/Si 式中,S表示同一组被试在两半测验上得分之差的方差 (2)库德一理查逊信度 该方法适合于测验题目全部为二分计分题的测验的内部一致性信度分析。库德一理查逊公 式有好几个,常用的是下面两个公式。 KR公式: KR-K-1S 式中,R0为测验的信度,K为题目数,P1和Q:分别表示答对和答错第1道题的被试人数 比例,S表示所有被试在整个测验上的总得分的方差。 KR,公式: K「,K-) KR2=K-1 式中,KR21为测验的信度,K为题目数,表示所有被试在整个测验上的总得分的均值
2 18 15 14 17 15 16 14 12 10 7 6 2 1 9 2 22 0 偶数题 2 17 18 20 17 16 13 14 13 12 8 8 1 2 3 2 18 0 奇数题 1 5 0 05 06 07 08 09 10 11 12 13 14 4 0 3 0 02 1 被试 计算两个“半测验”得分的积差相关系数为:0.86。代入公式得: 由于斯皮尔曼-布朗公式有个基本假设,即:两个“半测验”满足方差齐性,故,当数据 资料不能满足这一假设时,应选择下述两个等价的公式之一: ① 弗朗那根(Flanagan)公式 式中,Sa 2 和 Sb 2 分别表示所有被试在两半测验上得分的方差;SX 2 表示所有被试在整个 测验上的总得分的方差。 ②卢仑(Rulon)公式 式中, Sd 2 表示同一组被试在两半测验上得分之差的方差。 (2)库德-理查逊信度 该方法适合于测验题目全部为二分计分题的测验的内部一致性信度分析。库德-理查逊公 式有好几个,常用的是下面两个公式。 式中,KR20为测验的信度 ,K 为题目数,pi和 qi分别表示答对和答错第 i 道题的被试人数 比例,SX 2 表示所有被试在整个测验上的总得分的方差。 式中,KR21 为测验的信度 ,K 为题目数, 表示所有被试在整个测验上的总得分的均值。 rxx = 2rhh (1+ rhh ) = (2 0.86) (1+ 0.86) = 0.92 ( ) 2 2 2 xx 2 1 Sa Sb S X r = − + 2 2 xx 1 Sd S X r = − − − = 20 20 2 1 1 X i i S p q K K KR 公式: KR ( ) − − − = 21 21 2 1 1 KSX X K X K K KR 公式: KR
例:10名被试在某测验上的得分情况 被试分数 1 2 3 4 5 6 总分 01 1 1 02 40 0 4 0 0 2 03 0 0 0 0 1 1 2 04 1 1 0 05 01 0 0 4 1 3 1 1 3 7 44 1 4 0 n 4 08 11 4 n9 1 1 4 1 5 10 1 1 0.80.7 0.5 0.5 04 0.4 0.20.3 0.5 0.5 0.6 0.6 01021 025 025 024024 解:K=6 ∑P=1.35 S经=2.01代入公式 用同一数据,求得X=3.3代入公式: kg-386-031 说明:当测验中所有试题难度都一样或平均难度接近0.50时,上述两公式所估计的信度值将相 等,当试题难度值极不相同时,两公式所估计的信度值将差距较大,通常后者会小于前者 (3)克龙巴赫a系数 该方法适合于测验题目的题型较多,并非都是二分计分题的测验的内部一致性信度分 析。估计测验信度采用克龙巴赫α系数,其计算公式为:
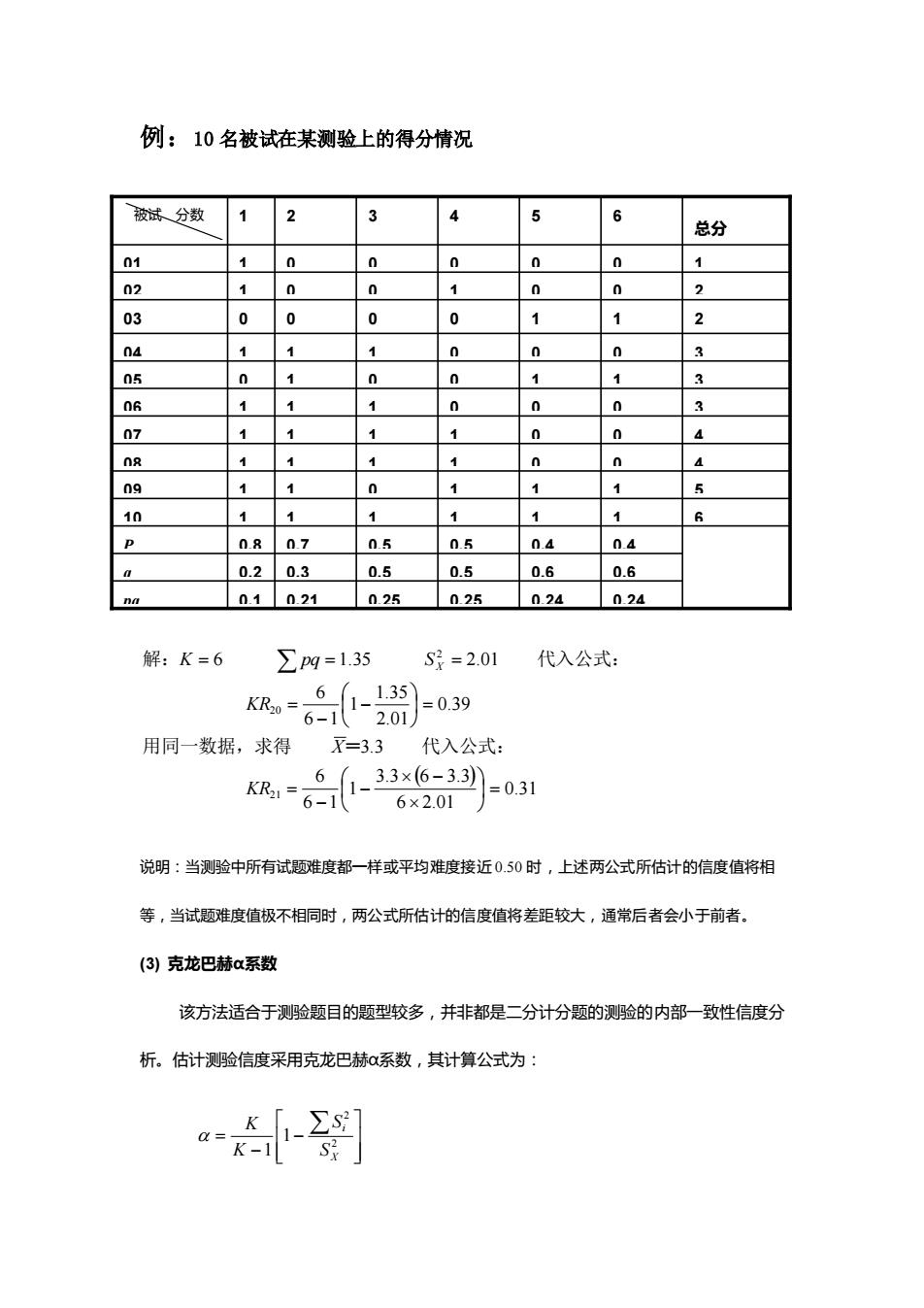
例:10 名被试在某测验上的得分情况 说明:当测验中所有试题难度都一样或平均难度接近 0.50 时,上述两公式所估计的信度值将相 等,当试题难度值极不相同时,两公式所估计的信度值将差距较大,通常后者会小于前者。 (3) 克龙巴赫α系数 该方法适合于测验题目的题型较多,并非都是二分计分题的测验的内部一致性信度分 析。估计测验信度采用克龙巴赫α系数,其计算公式为: 0.1 0.21 0.25 0.25 0.24 0.24 6 pq q 0.2 0.3 0.5 0.5 0.6 0.6 P 0.8 0.7 0.5 0.5 0.4 0.4 10 1 1 1 1 1 1 6 09 1 1 0 1 1 1 5 08 1 1 1 1 0 0 4 07 1 1 1 1 0 0 4 06 1 1 1 0 0 0 3 05 0 1 0 0 1 1 3 04 1 1 1 0 0 0 3 03 0 0 0 0 1 1 2 02 1 0 0 1 0 0 2 01 1 0 0 0 0 0 1 总分 被试 分数 1 2 3 4 5 6 ( ) 0.31 6 2.01 3.3 6 3.3 1 6 1 6 3.3 0.39 2.01 1.35 1 6 1 6 6 1.35 2.01 21 20 2 = − − − = = − − = = = = KR X KR K pq S X 用同一数据,求得 = 代入公式: 解: 代入公式: − − = 2 2 1 1 X i S S K K
式中,K为题目数,S2表示所有被试在第i道题上得分的方差,Sx表示所有被试在整个 测验上的总得分的方差。 例:5名被试在某测验上的得分情况 学生 sp 6 3.76 0.4 1.36 1.84 1R4 2.00 17 28 16 19 17 19.44 ∑S=3.76+0.4+1.36+1.84+1.84+2.00=1120 所有被试各自总分的方差S子=19.44 (4)荷伊特信度 云=1-s短 MS ·方差与标准差 1.基本概念 。一组数据中,各数离均差的平方和的算术平均数称为这组数据的方差,又叫均方差或变异 定义式: X(x,-x) S2=
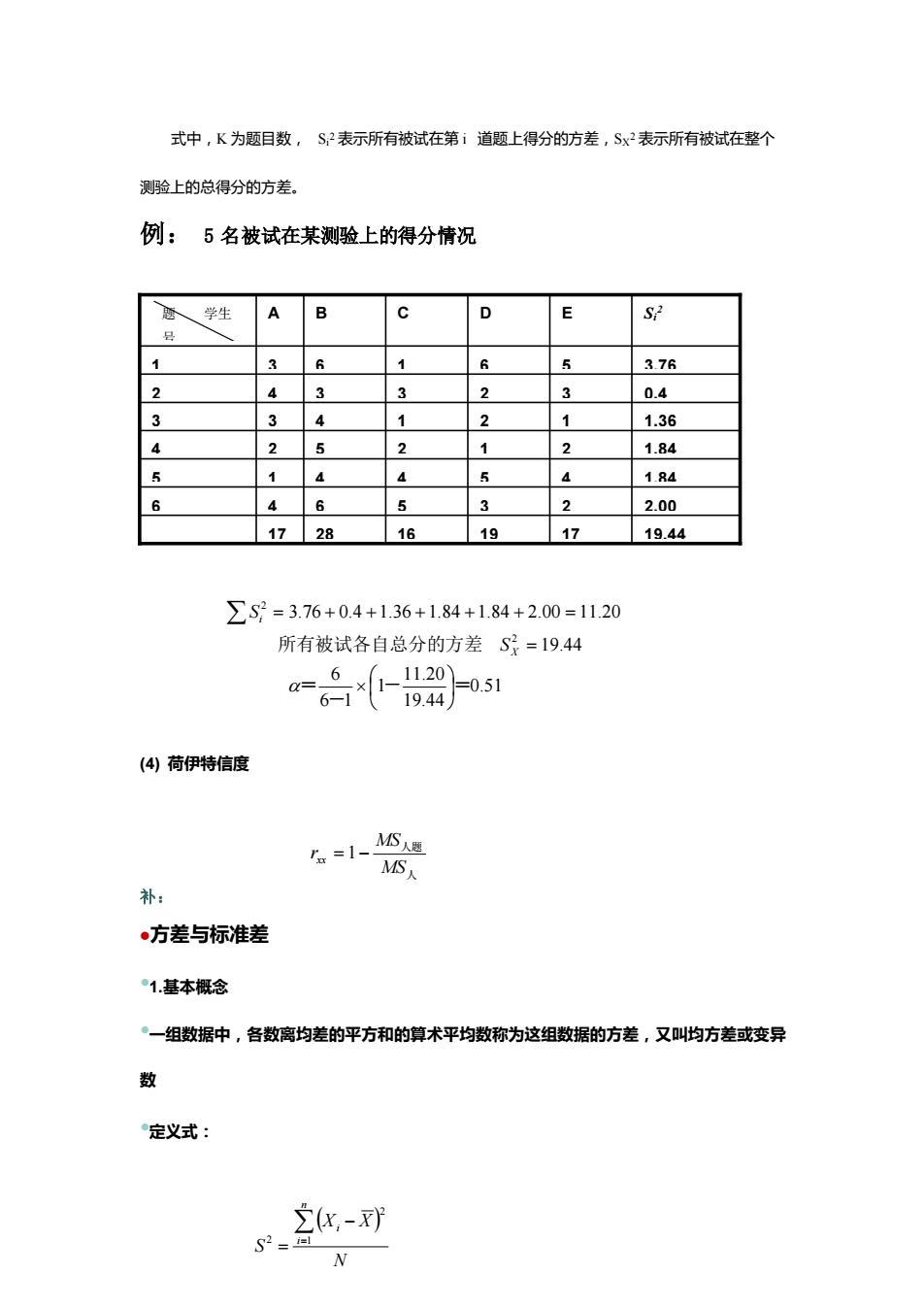
式中,K 为题目数, Si 2 表示所有被试在第 i 道题上得分的方差,SX 2 表示所有被试在整个 测验上的总得分的方差。 例: 5 名被试在某测验上的得分情况 (4) 荷伊特信度 补: ⚫方差与标准差 •1.基本概念 •一组数据中,各数离均差的平方和的算术平均数称为这组数据的方差,又叫均方差或变异 数 •定义式: 17 28 16 19 17 19.44 总分 6 4 6 5 3 2 2.00 5 1 4 4 5 4 1.84 4 2 5 2 1 2 1.84 3 3 4 1 2 1 1.36 2 4 3 3 2 3 0.4 1 3 6 1 6 5 3.76 Si 2 题 学生 A B C D E 号 0.51 19.44 11.20 1 6 1 6 19.44 3.76 0.4 1.36 1.84 1.84 2.00 11.20 2 2 - = - = 所有被试各自总分的方差 = = + + + + + = X i S S 人 人题 MS MS rxx = 1− ( ) N X X S n i i = − = 1 2 2

方差的算术平方根称为标准差 定义式: (x,-xY S=14 ●2.计算方差和标准差的简单方法 兴别 哥 最常用的相关系数公式: (1)积差相关系数公式(前已述) (2)等级相关系数公式 等级相关(等级差数法,或撕皮尔曼相关)是指以等级次序排列或以等级次序表示的变量 之间的相关 计算公试: D为二列数对等级的差数,N为总对数 适用条件 非连续变量中收集的资料是等级次序的 或连续变量,但其对数少于30,可按大小顺序排列编号 “说明:精确度稍差于积差相关
•方差的算术平方根称为标准差 •定义式: ⚫2.计算方差和标准差的简单方法 最常用的相关系数公式: (1)积差相关系数公式(前已述) (2)等级相关系数公式 等级相关(等级差数法,或斯皮尔曼相关)是指以等级次序排列或以等级次序表示的变量 之间的 相关 •计算公式: D 为二列数对等级的差数,N 为总对数 •适用条件: •非连续变量中收集的资料是等级次序的 •或连续变量,但其对数少于 30,可按大小顺序排列编号 •说明:精确度稍差于积差相关 ( ) N X X S n i i = − = 1 2 2 2 2 = − N X N X S 2 2 = − N X N X S ( 1) 6 1 2 2 − = − N N D rR
·检验:运用等级相关系数的临界值表进行检验 例:某项教改实验中,10名学生数学分数与物理分数等级相关系数计算表 Rx Ry D2 A 88 94 2 1 1 B 80 78 3 3.5 -0.5 0.25 68 56 5 8 3 9 D 60 48 8 9 -1 1 E 96 70 1 5.5 4.5 20.25 F 32 38 9.5 10 -0.5 0.25 G 32 62 9.5 7 2.5 6.25 H 64 78 6.5 3.5 3 9 64 70 6.55.5 1 1 小 75 82 4 2 2 4 54.52 6D =1-N衣可 (3)点二列相关系数公式 两列变量X、Y,一列属于连续变量,一列属于二分变量(如及格、不及格,对、错等) 这两列变量称为点二列或者点双列。 计算公式: 网 S 公式的说明 p为二分变量中某一类别在全部变量中所占的此例,q为另一类别所占的比例(q=1-p) Sx为全部连续变量X的标准差 ·点二列的始验,与积差相关相同
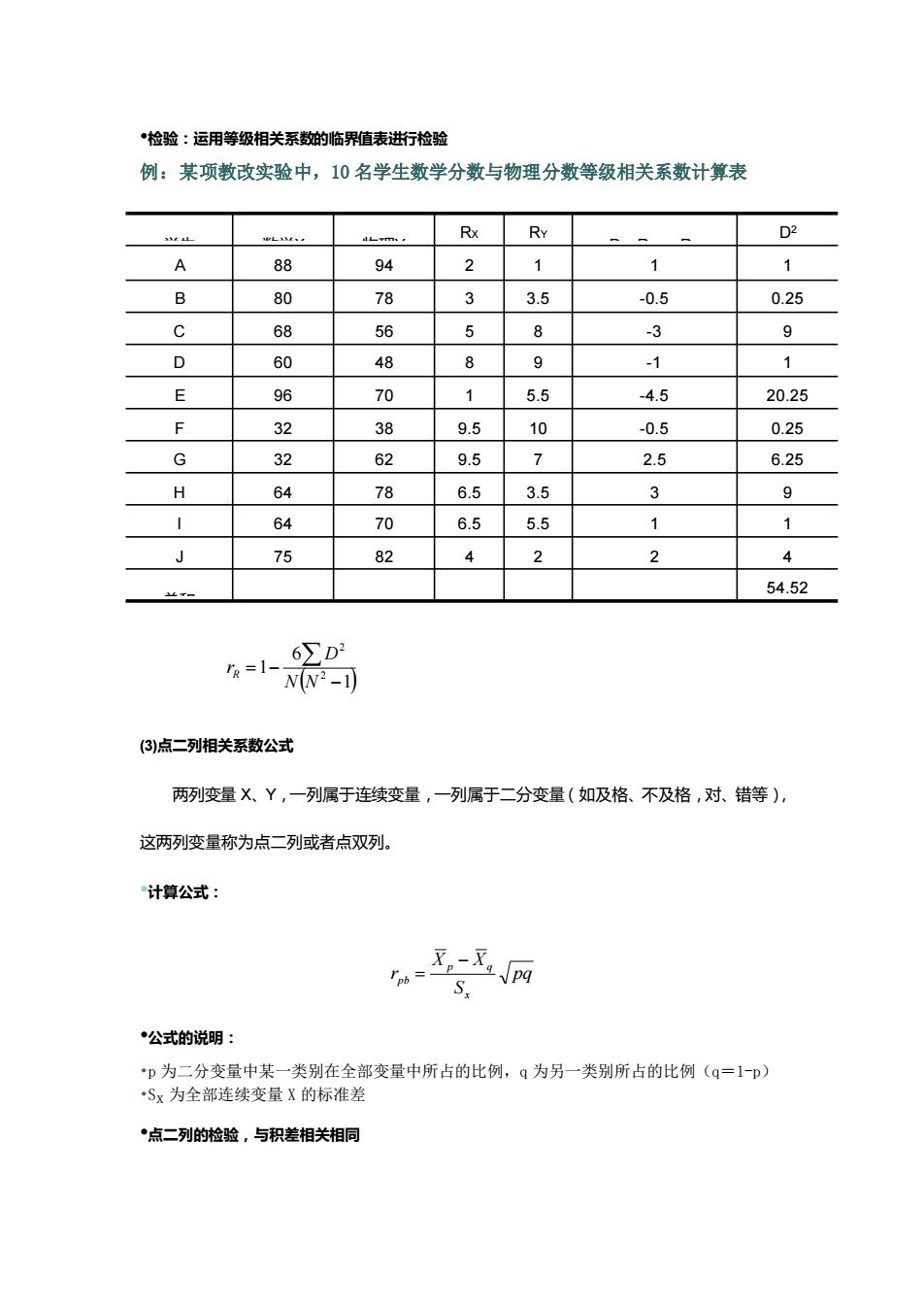
•检验:运用等级相关系数的临界值表进行检验 例:某项教改实验中,10 名学生数学分数与物理分数等级相关系数计算表 (3)点二列相关系数公式 两列变量 X、Y,一列属于连续变量,一列属于二分变量(如及格、不及格,对、错等), 这两列变量称为点二列或者点双列。 •计算公式: pq S X X r x p q pb − = •公式的说明: •p 为二分变量中某一类别在全部变量中所占的比例,q 为另一类别所占的比例(q=1-p) •Sx 为全部连续变量 X 的标准差 •点二列的检验,与积差相关相同 2 5.5 3.5 7 10 5.5 9 8 3.5 1 RY J 75 82 4 2 4 54.52 总和 I 64 70 6.5 1 1 H 64 78 6.5 3 9 G 32 62 9.5 2.5 6.25 F 32 38 9.5 -0.5 0.25 E 96 70 1 -4.5 20.25 D 60 48 8 -1 1 C 68 56 5 -3 9 B 80 78 3 -0.5 0.25 A 88 94 2 1 1 D2 D=RX- RY RX 学生 数学X 物理Y ( 1) 6 1 2 2 − = − N N D rR

例:一项学法研究欲分析课前预习对学习成绩的影响,预习与否以1/0表示, 个周期后16名学生的学习成绩如下表所示 学生 12345678910111213141516 学习成绩97927568749978807064879654 8693 80 预习情况011011010 1 0 1 0 1 0 预习者:p=9/16=0.564:不预习者:q=0.436 ,预习者的平均分:84.3:不预习者的平均分:77.3 ◆16名学生的标准差:Sx=13 由公式得地=0.27 查积差相关系数显著性临界值表,df=N-2=14,005=0.497 (4)二列相关系数公式 两列变量X、Y,都是正态连续变量,但其中一列变量可以被人为的分成二分变量,这时 两列变量之间的相关称为二列相关。 计算公式: 6-又四 S. 公式的说明: p为二分变量中某一类别在全部变量中所占的此例,q为另一类别所占的此例(q=1-p) S,为全部连续变量X的标准差 Y表示正态曲线下与P相对应的纵线高度。 ·点二列的检验,与积差相关相同
例:一项学法研究欲分析课前预习对学习成绩的影响,预习与否以 1/0 表示, 一个周期后 16 名学生的学习成绩如下表所示 ⚫预习者:p=9/16=0.564;不预习者:q=0.436 ⚫预习者的平均分:84.3;不预习者的平均分:77.3 ⚫16 名学生的标准差:Sx=13 ⚫由公式得 rpb=0.27 ⚫查积差相关系数显著性临界值表,df=N-2=14,r0.05=0.497 (4) 二列相关系数公式 两列变量 X、Y,都是正态连续变量,但其中一列变量可以被人为的分成二分变量,这时, 两列变量之间的相关称为二列相关。 •计算公式: •公式的说明: •p 为二分变量中某一类别在全部变量中所占的比例,q 为另一类别所占的比例(q=1-p) •Sx为全部连续变量 X 的标准差 •Y 表示正态曲线下与 P 相对应的纵线高度。 •点二列的检验,与积差相关相同 预习情况 0 1 1 0 1 1 0 1 0 1 0 1 0 1 1 0 学习成绩 97 92 75 68 74 99 78 80 70 64 87 96 54 86 93 80 学生 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 Y pq S X X r x p q b − =