
调查问卷的统计分析 2010.10
2010.10 调查问卷的统计分析

问卷的信度及计算 (一)信度的含义 ■信度是指测量结果的稳定性程度,记为'。 即:如果用同一测量工具反复测量同一种特质对象,则多次 测量结果间的一致性程度就叫信度。 测验信度是对测验工具及其操作的整体质量的一种量度,是 测验性能的重要质量指标。测量的一致性程度越高说明测量 结果越稳定,其可靠性越高 ■每次的测量结果实际包含被测的实际水平和测量误差两部分。 口物理测量:皮尺、钢尺、台秤、天平; 口教育和心理测量:各种测验量表; 口产生随机误差的因素:施测环境、完成时间、主被试关系、被 试的动机和情绪等;
一、问卷的信度及计算 (一)信度的含义 ◼ 信度是指测量结果的稳定性程度,记为 。 即:如果用同一测量工具反复测量同一种特质对象,则多次 测量结果间的一致性程度就叫信度。 ◼ 测验信度是对测验工具及其操作的整体质量的一种量度,是 测验性能的重要质量指标。测量的一致性程度越高说明测量 结果越稳定,其可靠性越高. ◼ 每次的测量结果实际包含被测的实际水平和测量误差两部分。 物理测量:皮尺、钢尺、台秤、天平; 教育和心理测量:各种测验量表; 产生随机误差的因素:施测环境、完成时间、主被试关系、被 试的动机和情绪等; xx r

问卷的信度及计算 (二)信度的估计方法 根据信度计算的不同方法,可将信度分为重测信度、复本信度、 同质性信度、评分者信度。 口重测信度 指用同一量表(测验或评价表)对同一组被试施测两次所得结果的一致 性程度。其大小等于同一组被试在两次测验上所得分数的相关系数, 一般采用皮尔逊积差相关的公式来计算。 重测信度的基本假设:.假设某测验所要测量的潜在特质,短期内不会 随时间推移而改变。故重测信度的高低和测量时间间隔长短密切相关。 间隔多久恰当呢?无固定标准,一般来说,在间隔时间内,被试的遗 忘和练习的效果基本上相互抵消,即为适度的时间间隔。 适用于速度测验而不适应于难度测验的信度估计
一、 问卷的信度及计算 (二)信度的估计方法 根据信度计算的不同方法,可将信度分为重测信度、复本信度、 同质性信度、评分者信度。 重测信度 指用同一量表(测验或评价表)对同一组被试施测两次所得结果的一致 性程度。其大小等于同一组被试在两次测验上所得分数的相关系数, 一般采用皮尔逊积差相关的公式来计算。 重测信度的基本假设:假设某测验所要测量的潜在特质,短期内不会 随时间推移而改变。故重测信度的高低和测量时间间隔长短密切相关。 间隔多久恰当呢?无固定标准,一般来说,在间隔时间内,被试的遗 忘和练习的效果基本上相互抵消,即为适度的时间间隔。 适用于速度测验而不适应于难度测验的信度估计

积差相关系数公式 N∑W-∑x∑Y Vw∑x2-∑xw∑Y2-∑ X为第一次测验的实得分数;Y为第二次测验的实得分数; N为被试人数。 口积差相关的运用条件: ■两个变量连续,且成线形关系 ■数据成对 ■两个变量的总体呈正态分布或至少为单峰对称分布 ■数据的对数最好在30对以上
积差相关系数公式 X为第一次测验的实得分数;Y为第二次测验的实得分数; N为被试人数。 积差相关的运用条件: ◼ 两个变量连续,且成线形关系 ◼ 数据成对 ◼ 两个变量的总体呈正态分布或至少为单峰对称分布 ◼ 数据的对数最好在30对以上 ( ) ( ) − − − = 2 2 2 2 N X X N Y Y N XY X Y rxx
例1:用某量表测验10名学生,得分记为X,为考察测量结 果的可靠性,于16天后用原量表对这10名同学再测一次,得 分记为Y,问测验结果是否可靠? 学生 X Y XY X2 Y2 A 88 94 8272 7744 8836 B 80 78 6240 6400 6084 C 68 56 3808 4624 3136 D 60 48 2880 3600 2304 E 96 70 6720 9216 4900 F 32 38 1216 1024 1444 G 32 62 1984 1024 3844 H 64 78 4992 4096 6084 64 70 4480 4096 4900 J 75 82 6151 5625 6724 总和 659 676 46742 47449 48256 计算得r=0.68
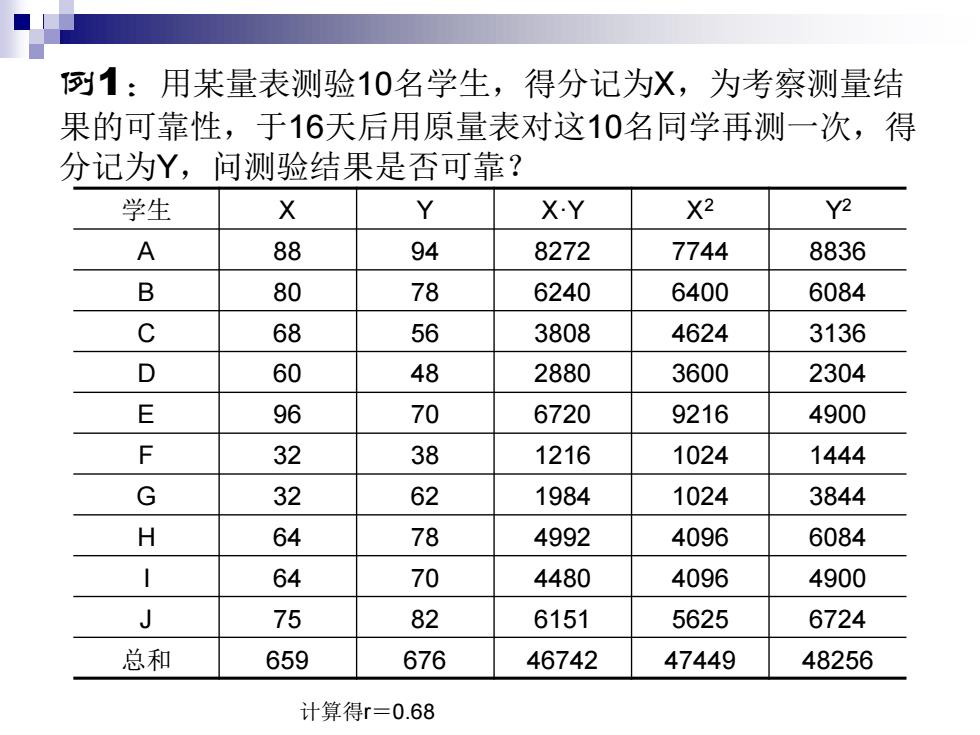
例1:用某量表测验10名学生,得分记为X,为考察测量结 果的可靠性,于16天后用原量表对这10名同学再测一次,得 分记为Y,问测验结果是否可靠? 学生 X Y X·Y X2 Y2 A 88 94 8272 7744 8836 B 80 78 6240 6400 6084 C 68 56 3808 4624 3136 D 60 48 2880 3600 2304 E 96 70 6720 9216 4900 F 32 38 1216 1024 1444 G 32 62 1984 1024 3844 H 64 78 4992 4096 6084 I 64 70 4480 4096 4900 J 75 82 6151 5625 6724 总和 659 676 46742 47449 48256 计算得r=0.68

重测信度的计算: 本例采用积差相关系数公式 N∑灯-∑X∑Y Vw∑x2-②xVw∑y2-(∑YY X为第一次测验的实得分数;Y为第二次测验的实得分数;N为被试人数。 10×46742-659×676 Yx= V10×47449-(659}V10×48256-(676} 计算得rxox=0.68,显著性水平取0.05, 查积差相关系数检验表得r0.05(8)=0.632,【x>r0.05(8), 说明两次测验所得分数显著相关,故该测验信度高,测验结果可 靠,作出此结论的可靠度为95%
重测信度的计算: 本例采用积差相关系数公式 X为第一次测验的实得分数;Y为第二次测验的实得分数;N为被试人数。 ( ) ( ) − − − = 2 2 2 2 N X X N Y Y N XY X Y rxx ( ) ( ) 2 2 10 47449 659 10 48256 676 10 46742 659 676 − − − rxx = 计算得rxx =0.68, 显著性水平取0.05, 查积差相关系数检验表得r0.05(8)=0.632, rxx>r0.05(8) , 说明两次测验所得分数显著相关,故该测验信度高,测验结果可 靠,作出此结论的可靠度为95%

例2一重测信度系数(稳定性系数)的计算 ■用一个算术四则的速度测验12个小学生,得分记 为X,为了考察测量结果的可靠性,于3个月后再 测一次,得分记为Y,问测验结果是否可靠? 学生序号123456789101112 X 202021222323232425262627 Y 202121202323252526262729
例2—重测信度系数(稳定性系数)的计算 ◼ 用一个算术四则的速度测验12个小学生,得分记 为X,为了考察测量结果的可靠性,于3个月后再 测一次,得分记为Y,问测验结果是否可靠? 学生序号 1 2 3 4 5 6 7 8 9 10 11 12 X 20 20 21 22 23 23 23 24 25 26 26 27 Y 20 21 21 20 23 23 25 25 26 26 27 29

重测信度的优缺点 优点: ■1、首测和再测只需要一套测验题目,比编制两套等值测 验题目要省力、省时。 ■2、同一套题目无论施测几次,所测量的属性是完全相同 的。 缺点: ■ 1、同一组被试对同一个测验先后两次作答相互之间是不 独立的。 ■2、两次施测的时间间隔较长,在此期间被试身心的发展、 新知识的获取都会使两次测验结果不同。 ■3、第二次测验时被试的兴趣减弱。 ■4、两次测验被试的主观状态不可能完全相同。 ■5、两次施测的环境不可能完全相同
重测信度的优缺点 优点: ◼ 1、首测和再测只需要一套测验题目,比编制两套等值测 验题目要省力、省时。 ◼ 2、同一套题目无论施测几次,所测量的属性是完全相同 的。 缺点: ◼ 1、同一组被试对同一个测验先后两次作答相互之间是不 独立的。 ◼ 2、两次施测的时间间隔较长,在此期间被试身心的发展、 新知识的获取都会使两次测验结果不同。 ◼ 3、第二次测验时被试的兴趣减弱。 ◼ 4、两次测验被试的主观状态不可能完全相同。 ◼ 5、两次施测的环境不可能完全相同

(二)信度的估计方法 口复本测验(平行测验): &试题题型、题数、难度、指导语说明、施测要求等方面都相当 &用来测量相同潜在特质或属性 &试题不相同 口复本信度指两个平行测验测量同一批被试所得结果的一致 性程度,其大小等于同一批被试在两个复本测验上所得分数 的相关系数。 口两种方式:同一时间连续施测;间隔一段时间后施测。 构造两份真正的平行测验很难! 适用于难度测验,也适用于速度测验的信度估计
复本测验(平行测验): &试题题型、题数、难度、指导语说明、施测要求等方面都相当 &用来测量相同潜在特质或属性 &试题不相同 复本信度指两个平行测验测量同一批被试所得结果的一致 性程度,其大小等于同一批被试在两个复本测验上所得分数 的相关系数。 两种方式:同一时间连续施测;间隔一段时间后施测。 构造两份真正的平行测验很难! 适用于难度测验,也适用于速度测验的信度估计。 (二)信度的估计方法
例3:假设对10名学生用两个等值的测验A、B施测, 测验实得分数分别用X和Y表示,测验结果如下:求 该测验的信度? 学生 X(A) Y(B) XY X2 Y2 1 74 76 5476 5776 5624 2 71 75 5041 5625 5325 3 72 71 5184 5041 5112 4 68 70 4624 4900 4760 5 76 76 5776 5776 5776 6 73 79 5329 6241 5767 7 67 65 4489 4225 4355 8 70 77 4900 5929 5390 9 65 62 4225 3844 4030 10 74 72 5476 5184 5328 总和∑ 710 723 50520 52541 51467
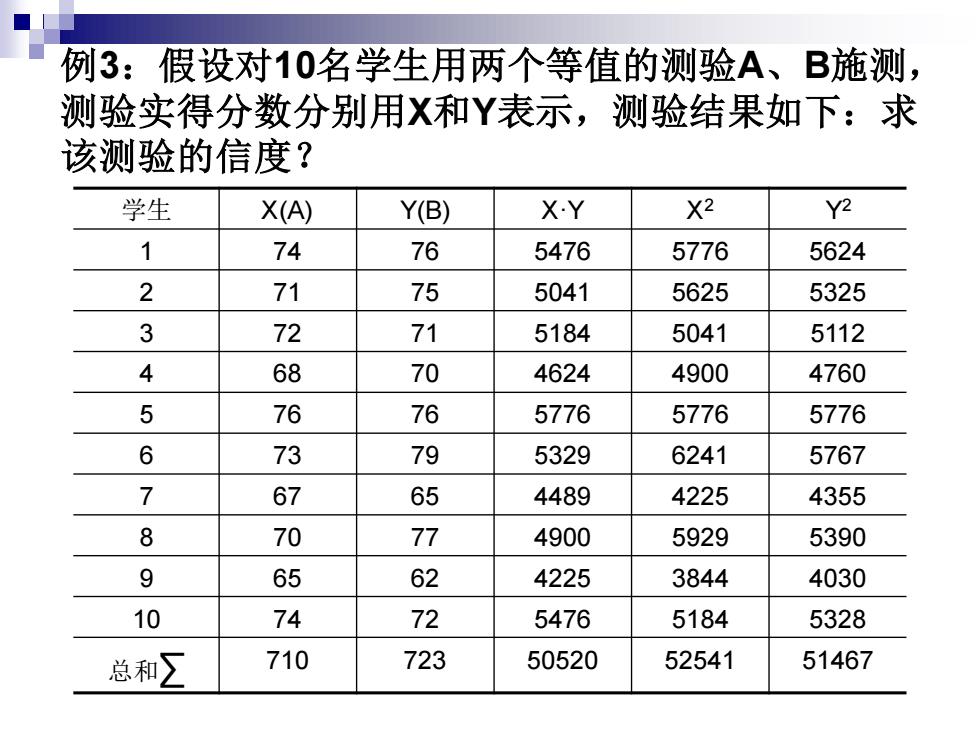
例3:假设对10名学生用两个等值的测验A、B施测, 测验实得分数分别用X和Y表示,测验结果如下:求 该测验的信度? 学生 X(A) Y(B) X·Y X2 Y2 1 74 76 5476 5776 5624 2 71 75 5041 5625 5325 3 72 71 5184 5041 5112 4 68 70 4624 4900 4760 5 76 76 5776 5776 5776 6 73 79 5329 6241 5767 7 67 65 4489 4225 4355 8 70 77 4900 5929 5390 9 65 62 4225 3844 4030 10 74 72 5476 5184 5328 总和∑ 710 723 50520 52541 51467