
第3章统计描述讲义 SPSS基本统计分析是进行其他统计分析的基础和前提。通过基本统计方法的学习,可 以对要分析数据的总体特征有比较准确的把握,从而有助于选择其他更为深入的统计分析方 法。 本章主要介绍如何在SPSS中进行平均数、中位数、众数、方差、百分位、须数、峰度 偏度、探索分析、交叉联列表分析、多选项分析、基本统计报表制作等的操作。 3.1均值(Mean)和均值标准误差(S.E.mean) 3.11统计学上的定义和计算公式 定义:均值(平均值、平均数)表示的是某变量所有取值的集中趋势或平均水平。例如, 学生某门学科的平均成绩、公司员工的平均收入、某班级学生的平均身高等。 计算公式如下。 总体平均数:若一组数据X1,X2,XN,代表一个大小为N的有限总体,则其总 体平均数为 样本平均数:若一组数据xl,x2,.,m,代表一个大小为n的有限样本,则其样本平 均数为 样本数据来自总体。样本的统计描述量可以反映总体数据的特征,但由于抽样等原因, 使得样本数据不一定能够完全准确地反映总体,它可能与总体的真实值之间存在一定的差 异。进行不同次抽样,会得到若干个不同的样本均值,它们与总体均值存在着不同的差异。 均值标准误差(Standard Error of Mean,S.E.mean)就是描述这些样本均值与总体 均值之间平均差异程度的统计量。 3.1.2SPSS中实现过程 研究问题 求某班级学生在一次数学测验中的平均成绩,数据如表31所示。 数学成绩 9988795954897956899923897050 67788956 表31某班级的数学成绩 实现步骤 图3-l在菜单中选择“Frequencies”命令 图3-2“Frequencies”对话框(一) 图3-3“Frequencies:Statistics”对话框(一) 3.13结果和讨论
第 3 章 统计描述讲义 SPSS 基本统计分析是进行其他统计分析的基础和前提。通过基本统计方法的学习,可 以对要分析数据的总体特征有比较准确的把握,从而有助于选择其他更为深入的统计分析方 法。 本章主要介绍如何在 SPSS 中进行平均数、中位数、众数、方差、百分位、频数、峰度、 偏度、探索分析、交叉联列表分析、多选项分析、基本统计报表制作等的操作。 3.1 均值(Mean)和均值标准误差(S.E.mean) 3.1.1 统计学上的定义和计算公式 定义:均值(平均值、平均数)表示的是某变量所有取值的集中趋势或平均水平。例如, 学生某门学科的平均成绩、公司员工的平均收入、某班级学生的平均身高等。 计算公式如下。 总体平均数:若一组数据 X1,X2,.,XN,代表一个大小为 N 的有限总体,则其总 体平均数为 样本平均数:若一组数据 x1,x2,.,xn,代表一个大小为 n 的有限样本,则其样本平 均数为 样本数据来自总体。样本的统计描述量可以反映总体数据的特征,但由于抽样等原因, 使得样本数据不一定能够完全准确地反映总体,它可能与总体的真实值之间存在一定的差 异。进行不同次抽样,会得到若干个不同的样本均值,它们与总体均值存在着不同的差异。 均值标准误差(Standard Error of Mean,S.E. mean)就是描述这些样本均值与总体 均值之间平均差异程度的统计量。 3.1.2 SPSS 中实现过程 研究问题 求某班级学生在一次数学测验中的平均成绩,数据如表 3-1 所示。 数 学 成 绩 99 88 79 59 54 89 79 56 89 99 23 89 70 50 67 78 89 56 表 3-1 某班级的数学成绩 实现步骤 图 3-1 在菜单中选择“Frequencies”命令 图 3-2 “Frequencies”对话框(一) 图 3-3 “Frequencies:Statistics”对话框(一) 3.1.3 结果和讨论

3.2中位数(Median) 32.1统计学上的定义和计算公式 定义:把一组数据按递增或递减的顺序排列,处于中间位置上的变量值就是中位数。它 是一种位置代表值,所以不会受到极端数值的影响,具有较高的稳健性 计算公式:一个大小为的数列,要求其中位数,首先应把该数列按大小顺序排列好,如 果为奇数,那么该数列的中位数就是位置上的数:如果N为偶数,中位数则是该数列中 第与第+1位置上两个数值的平均数。 3.2.2SPSS中实现过程 研究问题 求某班级学生身高的中位数,数据如表32所示。 表3-2某班级学生的身高 身高(cm) 174168164174176150183162171146 189167 实现步骤 图3-4“Frequencies:Statistics”对话框(二) 32.3结果和时论 3.3众数(Mode) 3.3.1统计学上的定义和计算公式 定义:众数是指一组数据中,出现次数最多的那个变量值。众数在描述数据集中趋势方 面有一定的意义。例如,制鞋厂可以根据消费者所需鞋的尺码的众数来安排生产。 计算公式:手工计算众数比较麻烦,需要统计数据的次数分布。 3.3.2SSS中实现过程 研究问愿 求某医院当天出生新生儿的体重的众数,数据如表33所示 表33新生儿的体重 体重(斤) 876754568756 765.57 4 实现步 图3-5“Frequencies.Statistics”对话框(三) 33.3结果和讨论
3.2 中位数(Median) 3.2.1 统计学上的定义和计算公式 定义:把一组数据按递增或递减的顺序排列,处于中间位置上的变量值就是中位数。它 是一种位置代表值,所以不会受到极端数值的影响,具有较高的稳健性。 计算公式:一个大小为的数列,要求其中位数,首先应把该数列按大小顺序排列好,如 果为奇数,那么该数列的中位数就是位置 上的数;如果 N 为偶数,中位数则是该数列中 第 与第 +1 位置上两个数值的平均数。 3.2.2 SPSS 中实现过程 研究问题 求某班级学生身高的中位数,数据如表 3-2 所示。 表 3-2 某班级学生的身高 身高(cm) 174 168 164 174 176 150 183 162 171 146 189 167 实现步骤 图 3-4 “Frequencies:Statistics”对话框(二) 3.2.3 结果和讨论 3.3 众数(Mode) 3.3.1 统计学上的定义和计算公式 定义:众数是指一组数据中,出现次数最多的那个变量值。众数在描述数据集中趋势方 面有一定的意义。例如,制鞋厂可以根据消费者所需鞋的尺码的众数来安排生产。 计算公式:手工计算众数比较麻烦,需要统计数据的次数分布。 3.3.2 SPSS 中实现过程 研究问题 求某医院当天出生新生儿的体重的众数,数据如表 3-3 所示。 表 3-3 新生儿的体重 体重(斤) 8 7 6 7 5 4 5 6 8 7 5 6 4 7 6 5.5 7 4 实现步骤 图 3-5 “Frequencies:Statistics”对话框(三) 3.3.3 结果和讨论

3.4全距(Rage) 3.4.1统计学上的定义和计算公式 定义:全距也称为极差,是数据的最大值与最小值之间的绝对差。在相同样本容量情况 下的两组数据,全距大的一组数据要比全距小的一组数据更为分散: 计算公式:最大值一最小值。 3.4.2SPSS中实现过程 研究问题 求某班级学生数学成绩的全距,数据如表34所示。 表34某班级的数学成绩 数学成绩 99887959548979568999238970 50 67788956 实现步骤 图3-6“Frequencies:.Statistics”对话框(四) 3.43结果和讨论 3.5方差(Variance)和标准差(Standard Deviation) 35.1统计学上的定义和计算公式 定义:方差是所有变量值与平均数偏差平方的平均值,它表示了一组数据分布的离散程 度的平均值。标准差是方差的平方根,它表示了一组数据关于平均数的平均离散程度。方差 和标准差越大,说明变量值之间的差异越大,距离平均数这个“中心”的离散趋势越大。 3.5.2SPSS中实现过程 研究问题 求某班级学生数学成绩的方差和标准差,数据如表31所示。 实现步骤 图3-7在菜单中选择“Descriptives”命令 图3-8“Descriptives”对话框(一) 图3-9“Descriptives::Options”对话框(一) 3.5.3结果和讨论 3.6四分位数(Quartiles)?、十分位数(Deciles)和百分位数(Percentiles) 3.6.1统计学上的定义 定义:四分位数是将一组个案由小到大(或由大到小)排序后,用3个点将全部数据分 为四等份,与3个点上相对应的变量称为四分位数,分别记为Q1(第一四分位数)、Q2(第
3.4 全距(Range) 3.4.1 统计学上的定义和计算公式 定义:全距也称为极差,是数据的最大值与最小值之间的绝对差。在相同样本容量情况 下的两组数据,全距大的一组数据要比全距小的一组数据更为分散。 计算公式:最大值-最小值。 3.4.2 SPSS 中实现过程 研究问题 求某班级学生数学成绩的全距,数据如表 3-4 所示。 表 3-4 某班级的数学成绩 99 88 79 59 54 89 79 56 89 99 23 89 70 50 67 78 89 56 实现步骤 图 3-6 “Frequencies:Statistics”对话框(四) 3.4.3 结果和讨论 3.5 方差(Variance)和标准差(Standard Deviation) 3.5.1 统计学上的定义和计算公式 定义:方差是所有变量值与平均数偏差平方的平均值,它表示了一组数据分布的离散程 度的平均值。标准差是方差的平方根,它表示了一组数据关于平均数的平均离散程度。方差 和标准差越大,说明变量值之间的差异越大,距离平均数这个“中心”的离散趋势越大。 3.5.2 SPSS 中实现过程 研究问题 求某班级学生数学成绩的方差和标准差,数据如表 3-1 所示。 实现步骤 图 3-7 在菜单中选择“Descriptives”命令 图 3-8 “Descriptives”对话框(一) 图 3-9 “Descriptives:Options”对话框(一) 3.5.3 结果和讨论 3.6 四分位数(Quartiles)、十分位数(Deciles)和百分位数(Percentiles) 3.6.1 统计学上的定义 定义:四分位数是将一组个案由小到大(或由大到小)排序后,用 3 个点将全部数据分 为四等份,与 3 个点上相对应的变量称为四分位数,分别记为 Q1(第一四分位数)、Q2(第

二四分位数)、Q3(第三四分位数)。其中,Q3到Q1之间的距离的一半又称为四分位差, 记为Q。四分位差越小,说明中间的数据越集中:四分位数越大,则意味着中间部分的数据 越分散。 十分位数是将一组数据由小到大(或由大到小)排序后,用9个点将全部数据分为十等 份,与9个点位置上相对应的变量称为十分位数,分别记为D1,D2,D9,表示10% 的数据落在D1下,20%的数据落在D2下,.,90%落在D9下。 百分位数是将一组数据由小到大(或由大到小)排序后分割为100等份,与99个分割 点位置上相对应的变量称为百分位数,分别记为P1,P2,.,P99,表示1%的数据落在P叫 下,2%的数据落在P2下,99%落在P99下。 3.6.2SPSS中实现过程 研究问题1 求某班级学生数学成绩的四分位数,数据如表31所示。 实现步骤 图3-10“Frequencies Statistics”对话框(五) 研究问题2 测量54个某种机械零件的重量(克),求零件重量的D6,数据如表35所示。 表35零件的重量 零件重量(克) 4651595446533752505149444944 43465647 5252504755494752524245406063 54405550 5646495346554445575250495548 58425259 实现步骤 图3-1l“Frequencies:Statistics”对话框(六) 图3-12“Frequencies::Statistics”对话框(七) 研究问题3 测量出54个某种机械零件的重量(克),求零件重量的P37,数据如表3-5所示 实现步骤 图3-12“Frequencies:Statistics”对话框(七) 3.63结果和讨论 研究问颗1的程序运行结果如下表所示
二四分位数)、Q3(第三四分位数)。其中,Q3 到 Q1 之间的距离的一半又称为四分位差, 记为 Q。四分位差越小,说明中间的数据越集中;四分位数越大,则意味着中间部分的数据 越分散。 十分位数是将一组数据由小到大(或由大到小)排序后,用 9 个点将全部数据分为十等 份,与 9 个点位置上相对应的变量称为十分位数,分别记为 D1,D2,.,D9,表示 10% 的数据落在 D1 下,20%的数据落在 D2 下,.,90%落在 D9 下。 百分位数是将一组数据由小到大(或由大到小)排序后分割为 100 等份,与 99 个分割 点位置上相对应的变量称为百分位数,分别记为 P1,P2,.,P99,表示 1%的数据落在 P1 下,2%的数据落在 P2 下,.,99%落在 P99 下。 3.6.2 SPSS 中实现过程 研究问题 1 求某班级学生数学成绩的四分位数,数据如表 3-1 所示。 实现步骤 图 3-10 “Frequencies:Statistics”对话框(五) 研究问题 2 测量 54 个某种机械零件的重量(克),求零件重量的 D6,数据如表 3-5 所示。 表 3-5 零件的重量 46 51 59 54 46 53 37 52 50 51 49 44 49 44 43 46 56 47 52 52 50 47 55 49 47 52 52 42 45 40 60 63 54 40 55 50 56 46 49 53 46 55 44 45 57 52 50 49 55 48 58 42 52 59 实现步骤 图 3-11 “Frequencies:Statistics”对话框(六) 图 3-12 “Frequencies:Statistics”对话框(七) 研究问题 3 测量出 54 个某种机械零件的重量(克),求零件重量的 P37,数据如表 3-5 所示。 实现步骤 图 3-12 “Frequencies:Statistics”对话框(七) 3.6.3 结果和讨论 研究问题 1 的程序运行结果如下表所示
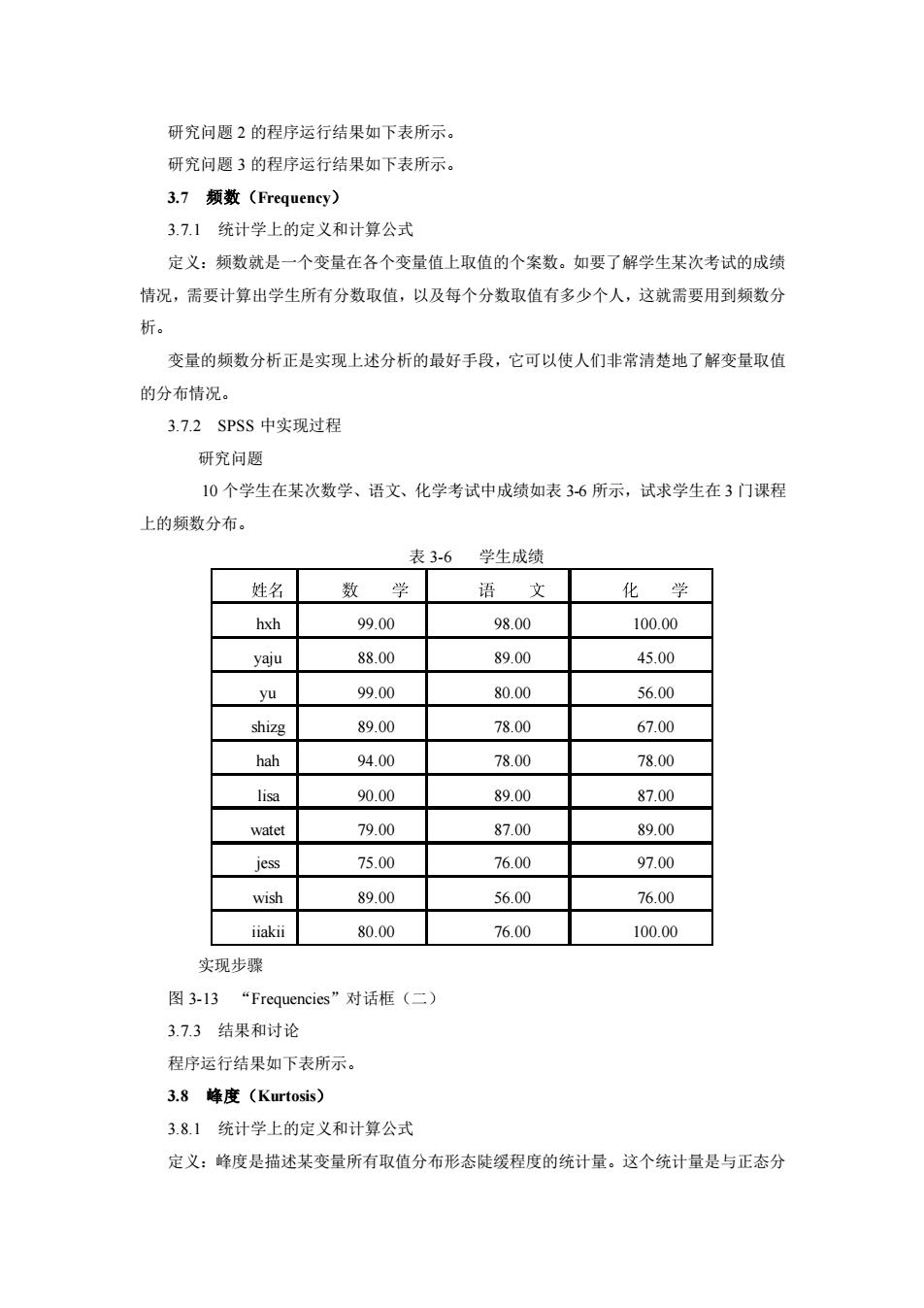
研究问题2的程序运行结果如下表所示。 研究问愿3的程序运行结果如下表所示。 3.7须数(Frequency) 3.71统计学上的定义和计算公式 定义:频数就是一个变量在各个变量值上取值的个案数。如要了解学生某次考试的成绩 情况,需要计算出学生所有分数取值,以及每个分数取值有多少个人,这就需要用到频数分 析。 变量的频数分析正是实现上述分析的最好手段,它可以使人们非常清楚地了解变量取值 的分布情况。 3.7.2SPSS中实现过程 研究问题 10个学生在某次数学、语文、化学考试中成绩如表3-6所示,试求学生在3门课程 上的频数分布。 表3-6学生成绩 姓名 数 语文 化学 hxh 99.00 98.00 100.00 yaju 88.00 89.00 45.00 yu 9900 80.00 56.00 shizg 89.00 78.00 67.00 hah 94.00 78.00 78.00 lisa 90.00 89.00 87.00 watet 79.00 87.00 89.00 jess 75.00 76.00 97.00 wish 89.00 56.00 76.00 iiakii 80.00 76.00 100.00 实现步骤 图3-13“Frequencies'”对话框(二) 3.7.3结果和讨论 程序运行结果如下表所示。 3.8峰度(Kurtosis) 3.8.1统计学上的定义和计算公式 定义:峰度是描述某变量所有取值分布形态陡缓程度的统计量。这个统计量是与正态分
研究问题 2 的程序运行结果如下表所示。 研究问题 3 的程序运行结果如下表所示。 3.7 频数(Frequency) 3.7.1 统计学上的定义和计算公式 定义:频数就是一个变量在各个变量值上取值的个案数。如要了解学生某次考试的成绩 情况,需要计算出学生所有分数取值,以及每个分数取值有多少个人,这就需要用到频数分 析。 变量的频数分析正是实现上述分析的最好手段,它可以使人们非常清楚地了解变量取值 的分布情况。 3.7.2 SPSS 中实现过程 研究问题 10 个学生在某次数学、语文、化学考试中成绩如表 3-6 所示,试求学生在 3 门课程 上的频数分布。 表 3-6 学生成绩 hxh 99.00 98.00 100.00 yaju 88.00 89.00 45.00 yu 99.00 80.00 56.00 shizg 89.00 78.00 67.00 hah 94.00 78.00 78.00 lisa 90.00 89.00 87.00 watet 79.00 87.00 89.00 jess 75.00 76.00 97.00 wish 89.00 56.00 76.00 iiakii 80.00 76.00 100.00 实现步骤 图 3-13 “Frequencies”对话框(二) 3.7.3 结果和讨论 程序运行结果如下表所示。 3.8 峰度(Kurtosis) 3.8.1 统计学上的定义和计算公式 定义:峰度是描述某变量所有取值分布形态陡缓程度的统计量。这个统计量是与正态分
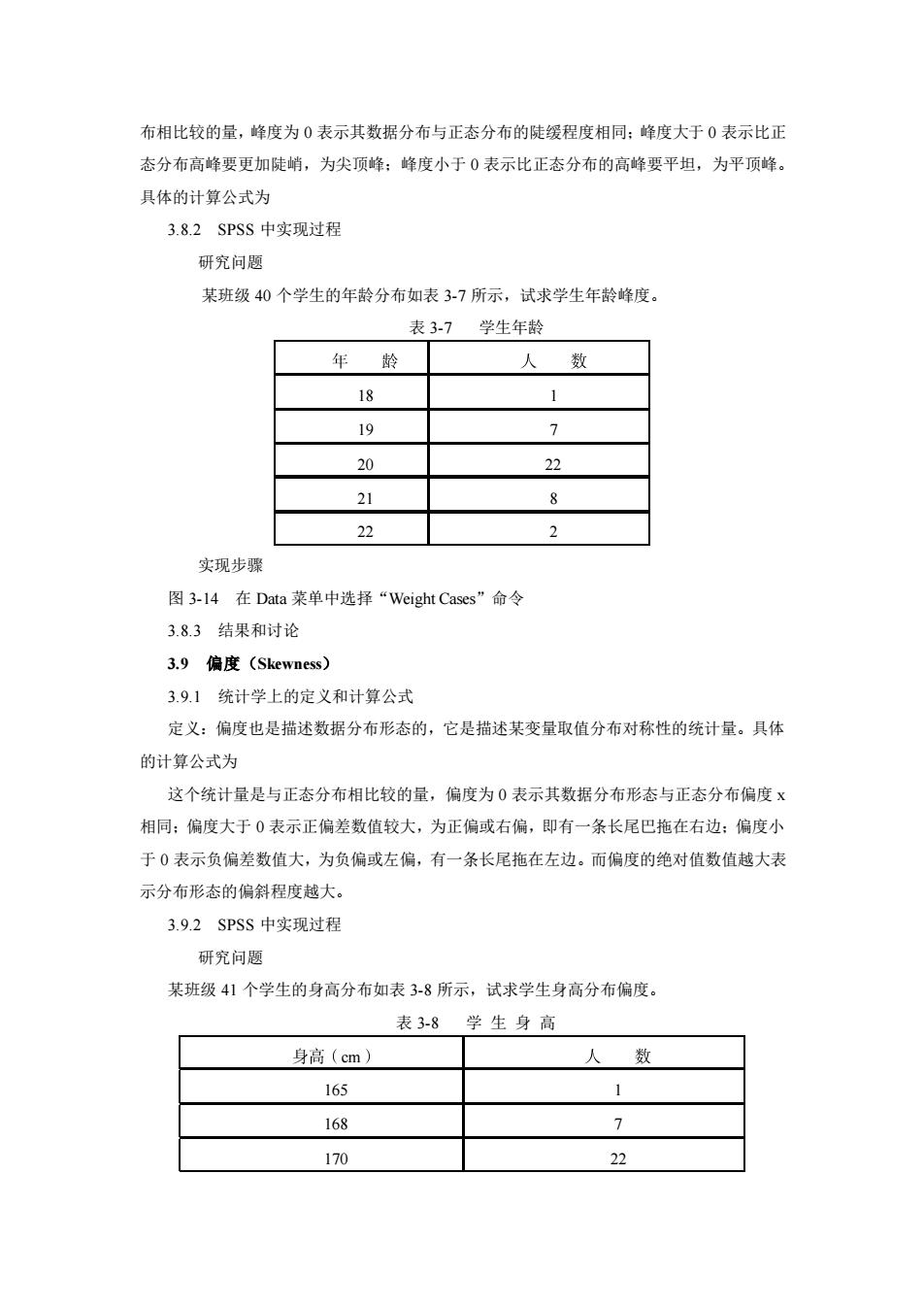
布相比较的量,峰度为0表示其数据分布与正态分布的陡缓程度相同:峰度大于0表示比正 态分布高峰要更加陡峭,为尖顶峰:峰度小于0表示比正态分布的高峰要平坦,为平顶峰 具体的计算公式为 3.8.2SPSS中实现过程 研究问题 某班级40个学生的年龄分布如表37所示,试求学生年龄蜂度。 表37学生年龄 年 龄 人数 18 1 19 7 20 22 21 8 22 2 实现步骤 图3-14在Data菜单中选择“Weight Cases”命令 3.83结果和讨论 3.9偏度(Skewness) 3.91统计学上的定义和计算公式 定义:偏度也是描述数据分布形态的,它是描述某变量取值分布对称性的统计量。具体 的计算公式为 这个统计量是与正态分布相比较的量,偏度为0表示其数据分布形态与正态分布偏度x 相同:偏度大于0表示正偏差数值较大,为正偏或右偏,即有一条长尾巴拖在右边:偏度小 于0表示负偏差数值大,为负偏或左偏,有一条长尾拖在左边。而偏度的绝对值数值越大表 示分布形态的偏斜程度越大。 3.9.2SPSS中实现过程 研究问题 某班级41个学生的身高分布如表38所示,试求学生身高分布偏度。 表3.8学生身高 身高(cm) 人 数 165 1 168 7 170 22
布相比较的量,峰度为 0 表示其数据分布与正态分布的陡缓程度相同;峰度大于 0 表示比正 态分布高峰要更加陡峭,为尖顶峰;峰度小于 0 表示比正态分布的高峰要平坦,为平顶峰。 具体的计算公式为 3.8.2 SPSS 中实现过程 研究问题 某班级 40 个学生的年龄分布如表 3-7 所示,试求学生年龄峰度。 表 3-7 学生年龄 18 1 19 7 20 22 21 8 22 2 实现步骤 图 3-14 在 Data 菜单中选择“Weight Cases”命令 3.8.3 结果和讨论 3.9 偏度(Skewness) 3.9.1 统计学上的定义和计算公式 定义:偏度也是描述数据分布形态的,它是描述某变量取值分布对称性的统计量。具体 的计算公式为 这个统计量是与正态分布相比较的量,偏度为 0 表示其数据分布形态与正态分布偏度 x 相同;偏度大于 0 表示正偏差数值较大,为正偏或右偏,即有一条长尾巴拖在右边;偏度小 于 0 表示负偏差数值大,为负偏或左偏,有一条长尾拖在左边。而偏度的绝对值数值越大表 示分布形态的偏斜程度越大。 3.9.2 SPSS 中实现过程 研究问题 某班级 41 个学生的身高分布如表 3-8 所示,试求学生身高分布偏度。 表 3-8 学 生 身 高 cm 165 1 168 7 170 22

173 175 180 实现步骤 图3-l7“Frequencies Statistics”对话框(九) 3.9.3结果和讨论 3.10标准化乙分数及其线性转换 3.10.1统计学上的定义和计算公式 3.10.2SPSS中实现过程 研究问题1 求某班级学生数学成绩的乙分数,数据如表31所示。 实现步骤 图3-18“Descriptives”对话框(二) 图3-19“Descriptives:Options'”对话框(二) 图3-20数据编辑窗口 研究问题2 从图3-20中可以看到学生数学成绩的Z分数有正有负,而且小数点位数较多,因 此可以把它线性转换为T分数。 实现步骤 图3-21在菜单中选择“Compute Variable”命令 图3-22“Compute Variable”对话框 图3-23“Compute Variable:Type”对话框 图3-24数据编辑窗口 3.10.3结果和讨论 从Z分数(图3-20)和T分数(图3-24)的结果中可以看出此班级学生数学成绩的T 分数比之前的Z分数简洁多了,比较起来一目了然。 3.11探素分析 3.11.1统计学上的定义和计算公式 定义:调用此过程可对变量进行更为深入详尽的描述性统计分析,故称之为探索分析。 它在一般描述性统计指标的基础上,增加有关数据其他特征的文字与图形描述,显得更加细 致与全面,有助于用户思考对数据进行进一步分析的方案。 1.探索分析的内容包括下面几个方面 检查数据是否有错误:过大或过小的数据均有可能是奇异值、影响点或错误数据
173 8 175 2 180 1 实现步骤 图 3-17 “Frequencies:Statistics”对话框(九) 3.9.3 结果和讨论 3.10 标准化 Z 分数及其线性转换 3.10.1 统计学上的定义和计算公式 3.10.2 SPSS 中实现过程 研究问题 1 求某班级学生数学成绩的 Z 分数,数据如表 3-1 所示。 实现步骤 图 3-18 “Descriptives”对话框(二) 图 3-19 “Descriptives:Options”对话框(二) 图 3-20 数据编辑窗口 研究问题 2 从图 3-20 中可以看到学生数学成绩的 Z 分数有正有负,而且小数点位数较多,因 此可以把它线性转换为 T 分数。 实现步骤 图 3-21 在菜单中选择“Compute Variable”命令 图 3-22 “Compute Variable”对话框 图 3-23 “Compute Variable:Type”对话框 图 3-24 数据编辑窗口 3.10.3 结果和讨论 从 Z 分数(图 3-20)和 T 分数(图 3-24)的结果中可以看出此班级学生数学成绩的 T 分数比之前的 Z 分数简洁多了,比较起来一目了然。 3.11 探 索 分 析 3.11.1 统计学上的定义和计算公式 定义:调用此过程可对变量进行更为深入详尽的描述性统计分析,故称之为探索分析。 它在一般描述性统计指标的基础上,增加有关数据其他特征的文字与图形描述,显得更加细 致与全面,有助于用户思考对数据进行进一步分析的方案。 1.探索分析的内容包括下面几个方面 检查数据是否有错误:过大或过小的数据均有可能是奇异值、影响点或错误数据
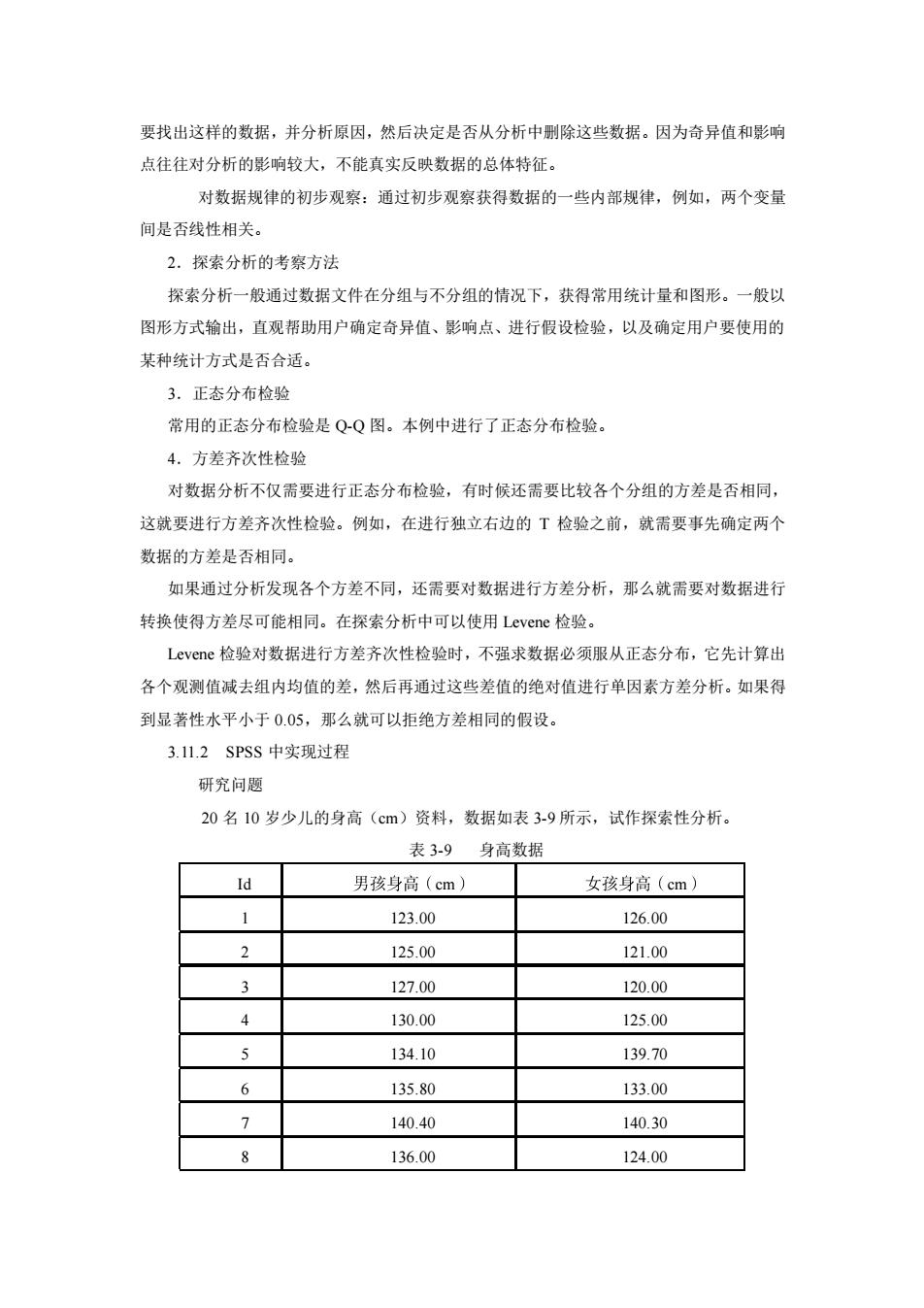
要找出这样的数据,并分析原因,然后决定是否从分析中别除这些数据。因为奇异值和影响 点往往对分析的影响较大,不能真实反映数据的总体特征。 对数据规律的初步观察:通过初步观察获得数据的一些内部规律,例如,两个变量 间是否线性相关。 2.探索分析的考察方法 探索分析一般通过数据文件在分组与不分组的情况下,获得常用统计量和图形。一般以 图形方式输出,直观帮助用户确定奇异值、影响点、进行假设检验,以及确定用户要使用的 某种统计方式是否合适。 3.正态分布检验 常用的正态分布检验是Q-Q图。本例中进行了正态分布检验。 4.方差齐次性检验 对数据分析不仅需要进行正态分布检验,有时候还需要比较各个分组的方差是否相同, 这就要进行方差齐次性检验。例如,在进行独立右边的T检验之前,就需要事先确定两个 数据的方差是否相同。 如果通过分析发现各个方差不同,还需要对数据进行方差分析,那么就需要对数据进行 转换使得方差尽可能相同。在探索分析中可以使用Levene检验。 Levene检验对数据进行方差齐次性检验时,不强求数据必须服从正态分布,它先计算出 各个观测值减去组内均值的差,然后再通过这些差值的绝对值进行单因素方差分析。如果得 到显著性水平小于0.05,那么就可以拒绝方差相同的假设。 3.112SPSS中实现过程 研究问题 20名10岁少儿的身高(cm)资料,数据如表3-9所示, 试作探索性分析。 表3-9身高数据 Id 男孩身高(cm)) 女孩身高(cm) 1 123.00 126.00 2 125.00 121.00 127.00 120.00 4 130.00 125.00 5 134.10 139.70 6 135.80 133.00 140.40 140.30 136.00 124.00
要找出这样的数据,并分析原因,然后决定是否从分析中删除这些数据。因为奇异值和影响 点往往对分析的影响较大,不能真实反映数据的总体特征。 对数据规律的初步观察:通过初步观察获得数据的一些内部规律,例如,两个变量 间是否线性相关。 2.探索分析的考察方法 探索分析一般通过数据文件在分组与不分组的情况下,获得常用统计量和图形。一般以 图形方式输出,直观帮助用户确定奇异值、影响点、进行假设检验,以及确定用户要使用的 某种统计方式是否合适。 3.正态分布检验 常用的正态分布检验是 Q-Q 图。本例中进行了正态分布检验。 4.方差齐次性检验 对数据分析不仅需要进行正态分布检验,有时候还需要比较各个分组的方差是否相同, 这就要进行方差齐次性检验。例如,在进行独立右边的 T 检验之前,就需要事先确定两个 数据的方差是否相同。 如果通过分析发现各个方差不同,还需要对数据进行方差分析,那么就需要对数据进行 转换使得方差尽可能相同。在探索分析中可以使用 Levene 检验。 Levene 检验对数据进行方差齐次性检验时,不强求数据必须服从正态分布,它先计算出 各个观测值减去组内均值的差,然后再通过这些差值的绝对值进行单因素方差分析。如果得 到显著性水平小于 0.05,那么就可以拒绝方差相同的假设。 3.11.2 SPSS 中实现过程 研究问题 20 名 10 岁少儿的身高(cm)资料,数据如表 3-9 所示,试作探索性分析。 表 3-9 身高数据 Id cm cm 1 123.00 126.00 2 125.00 121.00 3 127.00 120.00 4 130.00 125.00 5 134.10 139.70 6 135.80 133.00 7 140.40 140.30 8 136.00 124.00

9 128.20 125.40 10 137.40 137.50 11 135.50 120.90 12 129.00 138.80 13 132.20 138.60 14 140.90 141.40 15 129.30 137.50 16 130.00 137.00 17 121.40 133.40 18 131.50 132.70 19 132.60 130.10 20 129.20 136.70 实现步骤 图3-25在菜单中选择“Explore”命令 图3-26 “Explore”对话框 图3-27 “Explore.Statistics”对话柜 图3-28 “Explore:Plots”对话框 图3-29“Explorea:Options”对话框 3.11.3结果和讨论 在结果输出窗口中将看到如下统计数据。 (1)首先输出如下个案观察量摘要表,如下表所示。 (2)然后输出如下表格。 (3)接者输出如下4个不同权重下作中心趋势的粗略最大似然确定数, (4)再接若输出百分位数,也是分组后的百分位数,如下表所示。 (5)分别输出两个组中的最大5个数和最小5个数,并且包括这些值对应的D,如下 表所示。 (6)输出方差齐次性检验结果。 (7)系统还进行数据的茎叶情形描述。 图3-30男孩身高的茎叶图 图331女孩身高的茎叶图 (8)系统输出箱图,如图3-32所示。 图332箱图
9 128.20 125.40 10 137.40 137.50 11 135.50 120.90 12 129.00 138.80 13 132.20 138.60 14 140.90 141.40 15 129.30 137.50 16 130.00 137.00 17 121.40 133.40 18 131.50 132.70 19 132.60 130.10 20 129.20 136.70 实现步骤 图 3-25 在菜单中选择“Explore”命令 图 3-26 “Explore”对话框 图 3-27 “Explore: Statistics”对话框 图 3-28 “Explore:Plots”对话框 图 3-29 “Explore:Options”对话框 3.11.3 结果和讨论 在结果输出窗口中将看到如下统计数据。 (1)首先输出如下个案观察量摘要表,如下表所示。 (2)然后输出如下表格。 (3)接着输出如下 4 个不同权重下作中心趋势的粗略最大似然确定数, (4)再接着输出百分位数,也是分组后的百分位数,如下表所示。 (5)分别输出两个组中的最大 5 个数和最小 5 个数,并且包括这些值对应的 ID,如下 表所示。 (6)输出方差齐次性检验结果。 (7)系统还进行数据的茎叶情形描述。 图 3-30 男孩身高的茎叶图 图 3-31 女孩身高的茎叶图 (8)系统输出箱图,如图 3-32 所示。 图 3-32 箱图

(9)输出Spread vs.Level图,如图3-33所示。 图333 Spread vs.Level图 (10)输出身高正态概率图(Normal Q-QPlot of身高),如图3-34所示 图334男孩身高变量的正态概率图 图3-35女孩身高变量的正态概率图 (I1)输出离散正态概率图(Detrended NormalQ-QPlot of身高),男孩身高如图336 所示,女孩身高如图3-37所示。横坐标是身高,纵坐标是和正态分布的偏离。 图3-36男孩身高离散正态概率图 图3-37女孩身高离散正态概率图 3.12交叉列联表分析 3.12.1统计学上的定义和计算公式 定义:前面的分析都是对单个变量的数据分布情况进行分析。但在实际分析中,还需要 掌握多个变量在不同取值情况下的数据分布情况,从而进一步深入分析变量之间的相互影响 和关系,这种分析就称为交叉列联表分析。 交叉列联表分析除了列出交叉分组下的频数分布外,还需要分析两个变量之间是否具有 独立性或一定的相关性。要获得变量之间的相关性,仅仅靠频数分布的数据是不够的,还需 要借助一些变量间相关程度的统计量和一些非参数检验的方法。 常用的衡量变量间相关程度的统计量是简单相关系数(参见本书有关章节),但在交叉 列联表分析中,由于行列变量往往不是连续变量,不符合计算简单相关系数的前提条件。因 此需要根据变量的性质,选择其他的相关系数,如Kendall等级相关系数、Eta值等。 SPSS提供了多种适用于不同相关系数的相关关系,这些检验的零假设是:行和列变量 之间彼此独立,不存在显著的相关关系。SPSS将自动给出检验的相伴概率,如果相伴概率 小于显著性水平0.05,那么应拒绝零假设,认为行列变量之间彼此相关 计算公式如下。 (1)卡方统计量检验是常用的检验行列变量之间是否相关的方法。交叉列联表的卡方 检验零假设是:行列变量之间独立,计算公式为 卡方统计量服从(行数-1)×(列数-1)个自由度的卡方统计,SPSS在自动计算卡方 统计量后,还会给出相应的相关概率。 (2)Contingency coefficient:列联系数。用于名义变量之间的相关系数计算。计算公式 由卡方统计量修改而得,公式为 其中,N为样本系数 (3)Phi and Cramer‘sV:中系数。用于名义变量之间的相关系数计算。计算公式由卡 方统计量修改而得,公式为
(9)输出 Spread vs. Level 图,如图 3-33 所示。 图 3-33 Spread vs. Level 图 (10)输出身高正态概率图(Normal Q-Q Plot of 身高),如图 3-34 所示。 图 3-34 男孩身高变量的正态概率图 图 3-35 女孩身高变量的正态概率图 (11)输出离散正态概率图(Detrended Normal Q-Q Plot of 身高),男孩身高如图 3-36 所示,女孩身高如图 3-37 所示。横坐标是身高,纵坐标是和正态分布的偏离。 图 3-36 男孩身高离散正态概率图 图 3-37 女孩身高离散正态概率图 3.12 交叉列联表分析 3.12.1 统计学上的定义和计算公式 定义:前面的分析都是对单个变量的数据分布情况进行分析。但在实际分析中,还需要 掌握多个变量在不同取值情况下的数据分布情况,从而进一步深入分析变量之间的相互影响 和关系,这种分析就称为交叉列联表分析。 交叉列联表分析除了列出交叉分组下的频数分布外,还需要分析两个变量之间是否具有 独立性或一定的相关性。要获得变量之间的相关性,仅仅靠频数分布的数据是不够的,还需 要借助一些变量间相关程度的统计量和一些非参数检验的方法。 常用的衡量变量间相关程度的统计量是简单相关系数(参见本书有关章节),但在交叉 列联表分析中,由于行列变量往往不是连续变量,不符合计算简单相关系数的前提条件。因 此需要根据变量的性质,选择其他的相关系数,如 Kendall 等级相关系数、Eta 值等。 SPSS 提供了多种适用于不同相关系数的相关关系,这些检验的零假设是:行和列变量 之间彼此独立,不存在显著的相关关系。SPSS 将自动给出检验的相伴概率,如果相伴概率 小于显著性水平 0.05,那么应拒绝零假设,认为行列变量之间彼此相关。 计算公式如下。 (1)卡方统计量检验是常用的检验行列变量之间是否相关的方法。交叉列联表的卡方 检验零假设是:行列变量之间独立,计算公式为 卡方统计量服从(行数−1)×(列数−1)个自由度的卡方统计,SPSS 在自动计算卡方 统计量后,还会给出相应的相关概率。 (2)Contingency coefficient:列联系数。用于名义变量之间的相关系数计算。计算公式 由卡方统计量修改而得,公式为 其中,N 为样本系数 (3)Phi and Cramer‘s V:ψ系数。用于名义变量之间的相关系数计算。计算公式由卡 方统计量修改而得,公式为