
教育科研数据资 料的分析 师范学院教育系 任建华
教育科研数据资 料的分析 师范学院教育系 任建华

第一部分 教育统计学的 ■内容和几个基本概念 一、什么是教育统计学 统计学 ◆} 现代意义上的统计指的是对与随机现象有 关的数据资料进行收集、整理、计算和分析的 过程。统计学是研究统计原理和方法的科学
第一部分 教育统计学的 内容和几个基本概念 一、什么是教育统计学 统计学 现代意义上的统计指的是对与随机现象有 关的数据资料进行收集、整理、计算和分析的 过程。统计学是研究统计原理和方法的科学

概车纶与款理统外 随机现象 自然界所观察到的现象:确定性现象随机现象 1.确定性现象 在一定条件下必然发生 的现象称为确定性现象, 实例 “太阳不会从西边升起”, “水从高处流向低处”, “同性电荷必然互斥
在一定条件下必然发生 的现象称为确定性现象. “太阳不会从西边升起”, 1.确定性现象 “同性电荷必然互斥”, “水从高处流向低处”, 实例 自然界所观察到的现象: 确定性现象 随机现象 随机现象

概華论与款醒统外 “函数在间断点处不存在导数”等 确定性现象的特征■专条件完全决定结果 2.随机现象 在一定条件下可能出现也可能不出现的现象 称为随机现象, 实例1在相同条件下掷一枚均匀的硬币,观察 正反两面出现的情况. 结果有可能出现正面也可能出现反面
在一定条件下可能出现也可能不出现的现象 称为随机现象. 实例1 在相同条件下掷一枚均匀的硬币,观察 正反两面出现的情况. 2. 随机现象 “函数在间断点处不存在导数” 等. 结果有可能出现正面也可能出现反面. 确定性现象的特征 条件完全决定结果

概车纶与款理统外 实例2从一批含有正品 其结果可能为: 和次品的产品中任意抽取 正品、次品. 一个产品. 实例3过马路交叉口时, 可能遇上各种颜色的交通 指挥灯
实例2 从一批含有正品 和次品的产品中任意抽取 一个产品. 其结果可能为: 正品 、次品. 实例3 过马路交叉口时, 可能遇上各种颜色的交通 指挥灯

概華论与款醒硫外 实例4出生的婴儿可 能是男,也可能是女 实例5 明天的天气可 能是晴,也可能是多云 妆分 或雨 随机现象的特征条件不能完全决定结果
实例4 出生的婴儿可 能是男,也可能是女. 实例5 明天的天气可 能是晴 , 也可能是多云 或雨. 随机现象的特征 条件不能完全决定结果

概车纶与款理统外 随机现象在一次观察中出现什么结果具有偶 然性,但在大量试验或观察中,这种结果的出现具 有一定的统计规律性。 如何来研究随机现象? 随机现象是通过随机试验来研究的. 问题 什么是随机试验?
随机现象在一次观察中出现什么结果具有偶 然性, 但在大量试验或观察中, 这种结果的出现具 有一定的统计规律性 。 随机现象是通过随机试验来研究的. 问题 什么是随机试验? 如何来研究随机现象?

概率伦与款理统针「 随机试验 定义 在概率论中,把具有以下三个特征的试验称 为随机试验. 1.可以在相同的条件下重复地进行; 2.每次试验的可能结果不止一个,并且能事 先明确试验的所有可能结果; 3.进行一次试验之前不能确定哪一个结果 会出现
1. 可以在相同的条件下重复地进行; 2. 每次试验的可能结果不止一个,并且能事 先明确试验的所有可能结果; 3. 进行一次试验之前不能确定哪一个结果 会出现. 在概率论中,把具有以下三个特征的试验称 为随机试验. 定义 随机试验
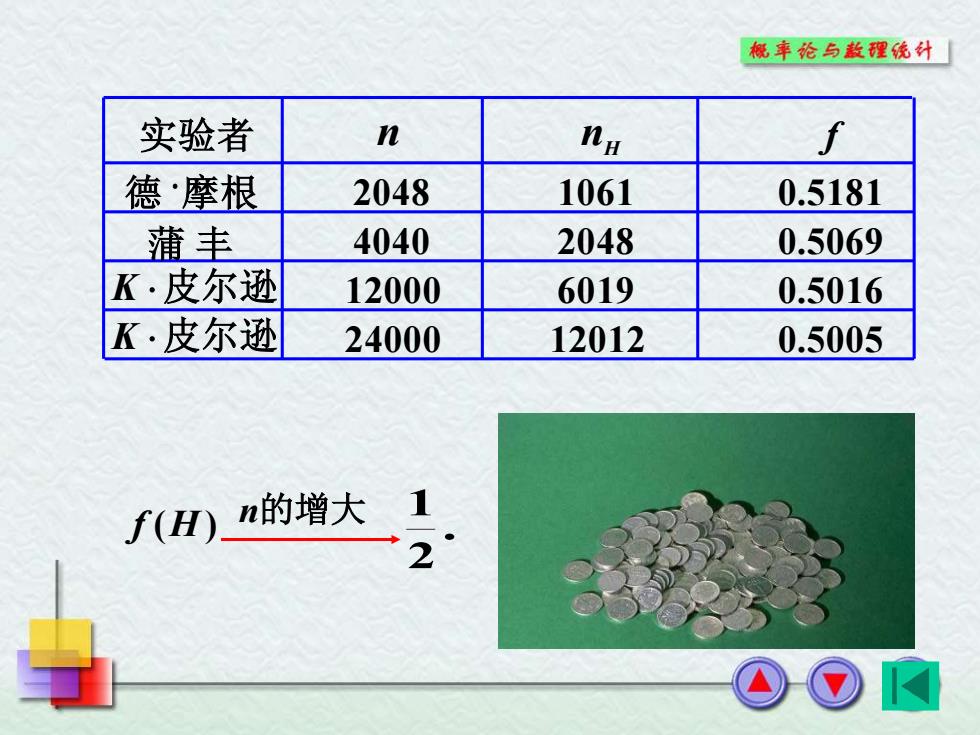
概率伦与散理统针 实验者 n na f 德·摩根 2048 1061 0.5181 蒲丰 4040 2048 0.5069 K·皮尔逊 12000 6019 0.5016 K·皮尔逊 24000 12012 0.5005 f(H)n的增大 1 2
实验者 德 摩根 蒲 丰 n nH f K 皮尔逊 K 皮尔逊 2048 1061 0.5181 4040 2048 0.5069 12000 6019 0.5016 24000 12012 0.5005 f ( H ) n的增大 . 21

统计学大致分为数理统计学和应用统计学两 部分。 数理统计学主要是以概率论为基础,对统计 数据数量关系的模式加以解释,对统计原理和方 法给予数学证明。 应用统计学研究如何运用数理统计学证明的 各种原理和方法解决实际问题
统计学大致分为数理统计学和应用统计学两 部分。 数理统计学主要是以概率论为基础,对统计 数据数量关系的模式加以解释,对统计原理和方 法给予数学证明。 应用统计学研究如何运用数理统计学证明的 各种原理和方法解决实际问题