
内蒙古农业大学食品科学与工程学院《食品工程原理》讲稿 CH4-§1 第四章 沉降与过滤 Sedimentation and Filtration 混合物分为两大类:均相物系(homogeneous system)和非均相 物系(non-homogeneous system)。凡物系内部各处物料组成和性质 均匀且不存在相界面的混合物称为均相物系。如溶液及混合气都属于 均相物系。凡物系内部有隔开两相的界面存在,且界面两侧的物料性 质截然不,称为非均相物系。悬浮液、乳浊液以及气溶胶等都属于非 均相物系。均相物系的分离可以通过蒸发、蒸馏、吸收和膜分离等单 元操作实现。将在以后的章节中讨论。本章主要讨论非均相物系的分 离。非均相物系中,处于分散状态的物质,称为分散质(或分散 相)Dispersed phase,如悬浮液中的固体颗粒,乳浊液中的液滴等; 包围着分散质而处于连续状态的物质称为分散介质 ( 或连续 相)continuous phase,如气态非均相混合物中的气体和液态非均相 物系中的溶剂等。藉分散质和分散介质所具有的不同的物理性质(如 密度)可使其分离。要实现这种分离,必须使分散的固体颗粒和液滴 与连续的流体之间发生相对运动,故可采用机械分离方。此种单元操 作遵循流体力学的基本规律。 在分离非均相物系的单元操作中,最主要是沉降法和过滤法。沉 降法是使气体或液体中的颗粒或液滴受重力或惯性离心力的作用而 沉降的方法。过滤法是利用液体或气体能通过过滤介质而固体颗粒不 1
内蒙古农业大学食品科学与工程学院《食品工程原理》讲稿 CH4-§1 第四章 沉降与过滤 Sedimentation and Filtration 混合物分为两大类:均相物系(homogeneous system)和非均相 物系(non-homogeneous system)。凡物系内部各处物料组成和性质 均匀且不存在相界面的混合物称为均相物系。如溶液及混合气都属于 均相物系。凡物系内部有隔开两相的界面存在,且界面两侧的物料性 质截然不,称为非均相物系。悬浮液、乳浊液以及气溶胶等都属于非 均相物系。均相物系的分离可以通过蒸发、蒸馏、吸收和膜分离等单 元操作实现。将在以后的章节中讨论。本章主要讨论非均相物系的分 离。非均相物系中,处于分散状态的物质,称为分散质(或分散 相)Dispersed phase,如悬浮液中的固体颗粒,乳浊液中的液滴等; 包围着分散质而处于连续状态的物质称为分散介质 ( 或连续 相)continuous phase,如气态非均相混合物中的气体和液态非均相 物系中的溶剂等。藉分散质和分散介质所具有的不同的物理性质(如 密度)可使其分离。要实现这种分离,必须使分散的固体颗粒和液滴 与连续的流体之间发生相对运动,故可采用机械分离方。此种单元操 作遵循流体力学的基本规律。 在分离非均相物系的单元操作中,最主要是沉降法和过滤法。沉 降法是使气体或液体中的颗粒或液滴受重力或惯性离心力的作用而 沉降的方法。过滤法是利用液体或气体能通过过滤介质而固体颗粒不 1

内蒙古农业大学食品科学与工程学院《食品工程原理》讲稿 CH4-§1 能穿过滤介质的性质进行分离的。沉降和过滤都可以在比重力场更强 的离心力场中进行。这种操作统称为离心分离。 沉降、过滤和离心分离在食品工业上具有如下的意义: (1) 作为生产的主要阶段。如从淀粉液制取淀粉,从牛奶制取奶 油和脱脂奶等。It is a main stage in the production (2) 提高制品纯度。如牛奶的除杂净化和啤酒的过滤净化除去微 粒固体等。Increasing purity of products (3) 回收有价值的物质。如从含微粒固体的气溶胶中分离出奶 粉。 extracting valuable matters (4) 为了安全生产。分离出生产中发生的酸雾、烟等有害物质, 保证人身和设备的安全。Removing harmful matters 第一节 重力沉降 Gravity Sedimentation 由于地球引力作用而产生分散质颗粒沉降的过程,称为重力沉降 (gravity settling)。 根据分散质集态的不同,可分为悬浮液、乳浊液和气溶胶的沉降。 乳浊液沉降中,有时分散质在分散介质中不是下沉,而是上浮。从相 对意义上说两者并无本质区别。要研究沉降的规律,首先应讨论颗粒 与流体的相对运动。 4—1 颗粒在流体中的运动 Movement of particles in fluid 4.1A 颗粒与流体相对运动时所受的力 The forces subjected by the particles during the relative movement between particles and fluid 2
内蒙古农业大学食品科学与工程学院《食品工程原理》讲稿 CH4-§1 能穿过滤介质的性质进行分离的。沉降和过滤都可以在比重力场更强 的离心力场中进行。这种操作统称为离心分离。 沉降、过滤和离心分离在食品工业上具有如下的意义: (1) 作为生产的主要阶段。如从淀粉液制取淀粉,从牛奶制取奶 油和脱脂奶等。It is a main stage in the production (2) 提高制品纯度。如牛奶的除杂净化和啤酒的过滤净化除去微 粒固体等。Increasing purity of products (3) 回收有价值的物质。如从含微粒固体的气溶胶中分离出奶 粉。 extracting valuable matters (4) 为了安全生产。分离出生产中发生的酸雾、烟等有害物质, 保证人身和设备的安全。Removing harmful matters 第一节 重力沉降 Gravity Sedimentation 由于地球引力作用而产生分散质颗粒沉降的过程,称为重力沉降 (gravity settling)。 根据分散质集态的不同,可分为悬浮液、乳浊液和气溶胶的沉降。 乳浊液沉降中,有时分散质在分散介质中不是下沉,而是上浮。从相 对意义上说两者并无本质区别。要研究沉降的规律,首先应讨论颗粒 与流体的相对运动。 4—1 颗粒在流体中的运动 Movement of particles in fluid 4.1A 颗粒与流体相对运动时所受的力 The forces subjected by the particles during the relative movement between particles and fluid 2

内蒙古农业大学食品科学与工程学院《食品工程原理》讲稿 CH4-§1 当流体以一定速度绕过静止的固体颗粒流动时,由于流体的粘 性,会对固颗粒有作用力。如图 4—1 所示。反之,当固体颗粒在静 止流体中移动时,流体同样会对固体颗粒有作用力。这两种情况作用 力的性质相同。通常称为曳力(drag force) 或阻力。除了上述两种 相对运动的情况外,还有运动着的颗粒与流动着的流体之间的相对运 动。对于一定的颗粒和流体,不论哪一种相对运动,都有这种阻力存 在。只要相对运动速度相同,流体对颗粒的阻力就一样. 图 4—1 颗粒与流体的相对运动 根据 Stockes 定律,连续流体以较低的速度流过球形颗粒所产生 的曳力可用下式表示: Fd=3πµ ud (N) (4—1) 式中: μ为流体粘度,Pa·s; d 为球形颗粒直径,m; u 为流体与颗粒间的相对运动速度,ms-1 ; Fd为流体对球形颗粒的曳力,N 上式只适用于流体对球形颗粒的绕流属于层流的情况。为求速度 范围更为广泛的曳力,可将式(4—1)改写为: 3
内蒙古农业大学食品科学与工程学院《食品工程原理》讲稿 CH4-§1 当流体以一定速度绕过静止的固体颗粒流动时,由于流体的粘 性,会对固颗粒有作用力。如图 4—1 所示。反之,当固体颗粒在静 止流体中移动时,流体同样会对固体颗粒有作用力。这两种情况作用 力的性质相同。通常称为曳力(drag force) 或阻力。除了上述两种 相对运动的情况外,还有运动着的颗粒与流动着的流体之间的相对运 动。对于一定的颗粒和流体,不论哪一种相对运动,都有这种阻力存 在。只要相对运动速度相同,流体对颗粒的阻力就一样. 图 4—1 颗粒与流体的相对运动 根据 Stockes 定律,连续流体以较低的速度流过球形颗粒所产生 的曳力可用下式表示: Fd=3πµ ud (N) (4—1) 式中: μ为流体粘度,Pa·s; d 为球形颗粒直径,m; u 为流体与颗粒间的相对运动速度,ms-1 ; Fd为流体对球形颗粒的曳力,N 上式只适用于流体对球形颗粒的绕流属于层流的情况。为求速度 范围更为广泛的曳力,可将式(4—1)改写为: 3

内蒙古农业大学食品科学与工程学院《食品工程原理》讲稿 CH4-§1 4 2 24 2 2 u du F d d ⋅ = ρ ⋅ ρ π µ 式中,ρ为流体的密度,kgm-3 。 令 µ duρ R ep = 4 2 d A π = R ep 24 ξ = Rep称为修正雷诺数, ξ称为阻力系数, A 为球形颗粒在相对运动方向的投影面积,m2 。 用这些关系将上式进一步整理可得: 2 2 u Fd A ρ = ξ (4—2) 对于层流, R ep 24 ξ = ,此时(4—2)与式(4—1)是相同的。对于非 层流的情况,阻力系数ξ要通过实验来确定。球形颗粒与流体相对运 动时的阻力系数ξ与雷诺数 Rep之间的关系由实验测定,绘于图 4—2 中。见图中对应于颗粒球形度φs=1 的曲线。 4
内蒙古农业大学食品科学与工程学院《食品工程原理》讲稿 CH4-§1 4 2 24 2 2 u du F d d ⋅ = ρ ⋅ ρ π µ 式中,ρ为流体的密度,kgm-3 。 令 µ duρ R ep = 4 2 d A π = R ep 24 ξ = Rep称为修正雷诺数, ξ称为阻力系数, A 为球形颗粒在相对运动方向的投影面积,m2 。 用这些关系将上式进一步整理可得: 2 2 u Fd A ρ = ξ (4—2) 对于层流, R ep 24 ξ = ,此时(4—2)与式(4—1)是相同的。对于非 层流的情况,阻力系数ξ要通过实验来确定。球形颗粒与流体相对运 动时的阻力系数ξ与雷诺数 Rep之间的关系由实验测定,绘于图 4—2 中。见图中对应于颗粒球形度φs=1 的曲线。 4
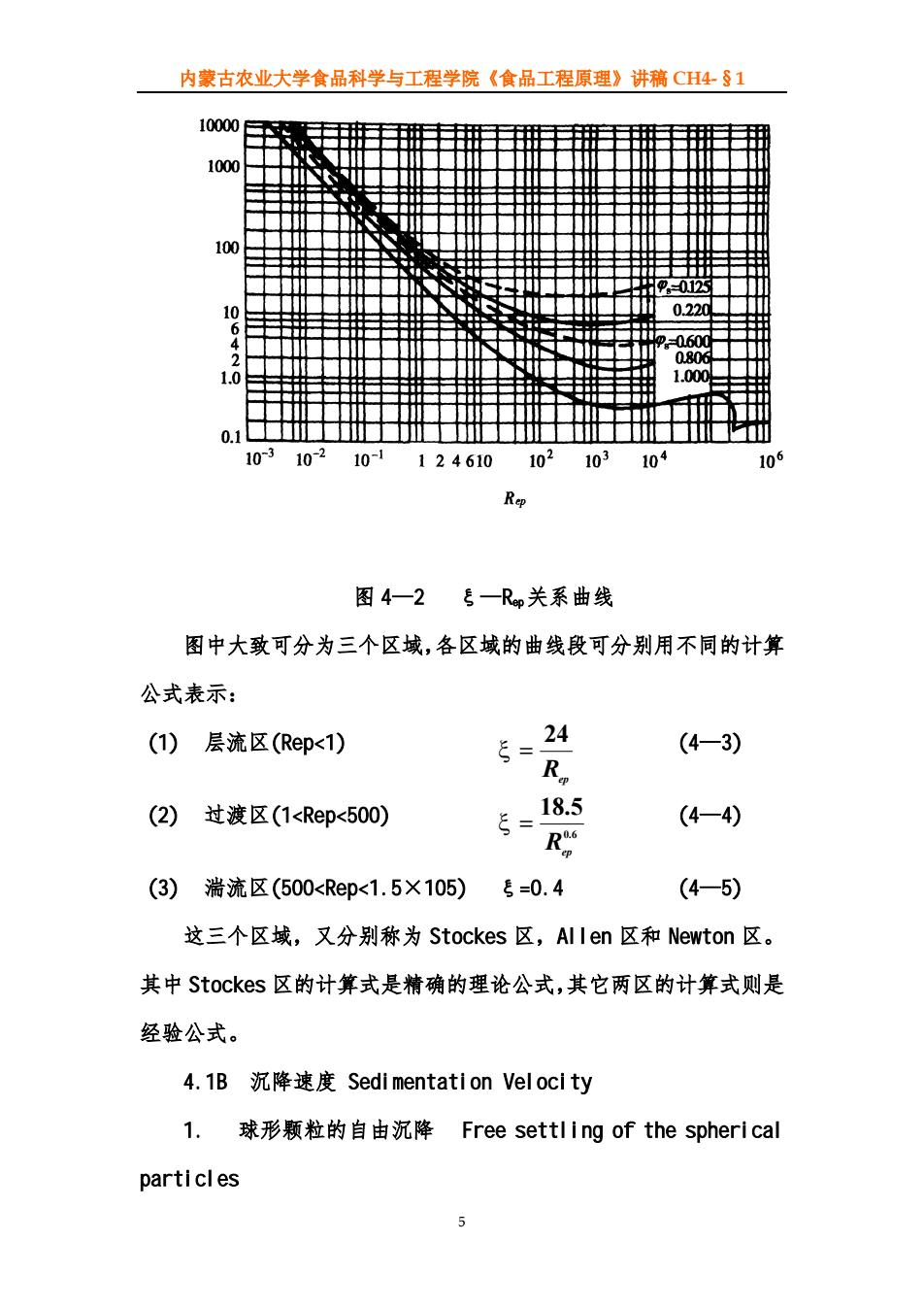
内蒙古农业大学食品科学与工程学院《食品工程原理》讲稿 CH4-§1 图 4—2 ξ—Rep关系曲线 图中大致可分为三个区域,各区域的曲线段可分别用不同的计算 公式表示: (1) 层流区(Rep<1) R ep 24 ξ = (4—3) (2) 过渡区(1<Rep<500) 0.6 18.5 R ep ξ = (4—4) (3) 湍流区(500<Rep<1.5×105) ξ=0.4 (4—5) 这三个区域,又分别称为 Stockes 区,Allen 区和 Newton 区。 其中 Stockes 区的计算式是精确的理论公式,其它两区的计算式则是 经验公式。 4.1B 沉降速度 Sedimentation Velocity 1. 球形颗粒的自由沉降 Free settling of the spherical particles 5
内蒙古农业大学食品科学与工程学院《食品工程原理》讲稿 CH4-§1 图 4—2 ξ—Rep关系曲线 图中大致可分为三个区域,各区域的曲线段可分别用不同的计算 公式表示: (1) 层流区(Rep<1) R ep 24 ξ = (4—3) (2) 过渡区(1<Rep<500) 0.6 18.5 R ep ξ = (4—4) (3) 湍流区(500<Rep<1.5×105) ξ=0.4 (4—5) 这三个区域,又分别称为 Stockes 区,Allen 区和 Newton 区。 其中 Stockes 区的计算式是精确的理论公式,其它两区的计算式则是 经验公式。 4.1B 沉降速度 Sedimentation Velocity 1. 球形颗粒的自由沉降 Free settling of the spherical particles 5

内蒙古农业大学食品科学与工程学院《食品工程原理》讲稿 CH4-§1 单个颗粒在无限连续的流体中沉降,或颗粒群在流体中分散得较 好,沉降时颗粒之间互不接触,互不碰撞,互不干扰,这种沉降称为 自由沉降(free settling)。 当一个球形颗粒放在静止流体中时,若其密度ρp 大于流体的密 度ρ时,它就向下沉降。 设该颗粒的直径为 d,质量为 m,初速度为零。在流体中下沉的 t 瞬时,它的速度为 u,所受的作用力有:重力 Fg,浮力 Fb 和流体的 阻力 Fd。其受力情况如图 4—3 所示。根据牛顿第二定律,颗粒的沉 降运动方程式为: Fd Fb mg 图 4—3 颗粒沉降受力图 F g Fb Fd d du m = − − τ (4—6a) 式中, F d g g ρ P π 3 6 = , (4—6b) F d g b ρ π 3 6 = , (4—6c) 6
内蒙古农业大学食品科学与工程学院《食品工程原理》讲稿 CH4-§1 单个颗粒在无限连续的流体中沉降,或颗粒群在流体中分散得较 好,沉降时颗粒之间互不接触,互不碰撞,互不干扰,这种沉降称为 自由沉降(free settling)。 当一个球形颗粒放在静止流体中时,若其密度ρp 大于流体的密 度ρ时,它就向下沉降。 设该颗粒的直径为 d,质量为 m,初速度为零。在流体中下沉的 t 瞬时,它的速度为 u,所受的作用力有:重力 Fg,浮力 Fb 和流体的 阻力 Fd。其受力情况如图 4—3 所示。根据牛顿第二定律,颗粒的沉 降运动方程式为: Fd Fb mg 图 4—3 颗粒沉降受力图 F g Fb Fd d du m = − − τ (4—6a) 式中, F d g g ρ P π 3 6 = , (4—6b) F d g b ρ π 3 6 = , (4—6c) 6

内蒙古农业大学食品科学与工程学院《食品工程原理》讲稿 CH4-§1 4 2 2 2 d u Fd π ρ = ξ ⋅ ⋅ 。 (4—6d) 将这些关系代入式沉降运动方程式为中,整理得: 2 4 3 u d g F F F d du m p p p g b d ρ ξρ ρ ρ ρ τ − − = = − − (4—6e) 由此式可知,右边第一项与 u 无关,第二项随 u 的增大而增大。 因此,随着颗粒向下沉降的速度 u 的逐渐增大,其加速度 dudt 则逐 渐减小。当 u 增加到某一数值 u0时,可使 du/dt=0。于是颗粒开始作 匀速沉降运动。可见颗粒的沉降过程分为两个阶段。起初为加速阶段, 而后为匀速阶段。对于小颗粒,加速阶段非常短,可以忽略不计,当 作只有均速阶段。在匀速阶段中颗粒相对于流体的运动速度 u0,称为 颗粒的沉降速度或终端速度(terminal velocity)。 当 du/dt=0 时,令 u=u0,由式(4—6)可得出球形颗粒自由沉降 速度的一般计算式: ( ) ξρ ρ ρ µ 3 4 0 d g u p − = (4-6) 将式(4—3),(4—4)和(4—5)的关系分别代入上式,可得到在 三个不同流型区域内球形颗粒自由沉降时沉降速度 u0 的计算公式: (1) 层流区的 Stockes 公式 7
内蒙古农业大学食品科学与工程学院《食品工程原理》讲稿 CH4-§1 4 2 2 2 d u Fd π ρ = ξ ⋅ ⋅ 。 (4—6d) 将这些关系代入式沉降运动方程式为中,整理得: 2 4 3 u d g F F F d du m p p p g b d ρ ξρ ρ ρ ρ τ − − = = − − (4—6e) 由此式可知,右边第一项与 u 无关,第二项随 u 的增大而增大。 因此,随着颗粒向下沉降的速度 u 的逐渐增大,其加速度 dudt 则逐 渐减小。当 u 增加到某一数值 u0时,可使 du/dt=0。于是颗粒开始作 匀速沉降运动。可见颗粒的沉降过程分为两个阶段。起初为加速阶段, 而后为匀速阶段。对于小颗粒,加速阶段非常短,可以忽略不计,当 作只有均速阶段。在匀速阶段中颗粒相对于流体的运动速度 u0,称为 颗粒的沉降速度或终端速度(terminal velocity)。 当 du/dt=0 时,令 u=u0,由式(4—6)可得出球形颗粒自由沉降 速度的一般计算式: ( ) ξρ ρ ρ µ 3 4 0 d g u p − = (4-6) 将式(4—3),(4—4)和(4—5)的关系分别代入上式,可得到在 三个不同流型区域内球形颗粒自由沉降时沉降速度 u0 的计算公式: (1) 层流区的 Stockes 公式 7

内蒙古农业大学食品科学与工程学院《食品工程原理》讲稿 CH4-§1 ( ) µ ρ ρ 18 2 0 d p − g u = (4—7) (2) 过渡区的 Allen 公式 ( ) 7 5 0.4 0.4 1.6 0 0.154 − = ρ µ d ρ ρ g u p (4—8) (3) 湍流区的 Newton 公式 ( ) ρ g ρ ρ gd p − = 3 u0 (4—9) 2 沉降速度的求算 Calculation of settling velocity 上面虽然给出了计算颗粒沉降速度 u0 的式(4—7)或(4—8)至(4 —9),但用这些公式计算时,须首先确定雷诺数 Rep的数值,这样才 能确定式(4—6)中的阻力系数ξ值;或者才能根据 Rep值所确定的流 型区域正确选用式(4—7)至(4—9)之中的某一计算式,而雷诺数 Rep 又正是要求算未知量 u0 的函数,故事先无法确定。可见计算沉降速 度 u0是较为复杂的。解算方法有如下几种: (1) 试差法(trial and error method) 先假定初值 u0,由 此算得 Rep 值,按图 4—2 查得ξ值,代入式(4—6)求得第一次试算 值 。比较u 值与假定值 u0。若二者非常接近或者二者之差的绝对 值能满足已定计算精度要求,则 即为最终计算值。若二者相差甚 远,需再次假定另一 u0 值,重复上述过程,直至假定值与计算值之 差的绝对值能满足已定精度要求为止。此法手算繁琐,但设计一个算 法程序,用计算机很容易求解。 u0 ′ 0 ′ u0 ′ (2) 复验法 (Repeat verification method)先假定一个流型 8
内蒙古农业大学食品科学与工程学院《食品工程原理》讲稿 CH4-§1 ( ) µ ρ ρ 18 2 0 d p − g u = (4—7) (2) 过渡区的 Allen 公式 ( ) 7 5 0.4 0.4 1.6 0 0.154 − = ρ µ d ρ ρ g u p (4—8) (3) 湍流区的 Newton 公式 ( ) ρ g ρ ρ gd p − = 3 u0 (4—9) 2 沉降速度的求算 Calculation of settling velocity 上面虽然给出了计算颗粒沉降速度 u0 的式(4—7)或(4—8)至(4 —9),但用这些公式计算时,须首先确定雷诺数 Rep的数值,这样才 能确定式(4—6)中的阻力系数ξ值;或者才能根据 Rep值所确定的流 型区域正确选用式(4—7)至(4—9)之中的某一计算式,而雷诺数 Rep 又正是要求算未知量 u0 的函数,故事先无法确定。可见计算沉降速 度 u0是较为复杂的。解算方法有如下几种: (1) 试差法(trial and error method) 先假定初值 u0,由 此算得 Rep 值,按图 4—2 查得ξ值,代入式(4—6)求得第一次试算 值 。比较u 值与假定值 u0。若二者非常接近或者二者之差的绝对 值能满足已定计算精度要求,则 即为最终计算值。若二者相差甚 远,需再次假定另一 u0 值,重复上述过程,直至假定值与计算值之 差的绝对值能满足已定精度要求为止。此法手算繁琐,但设计一个算 法程序,用计算机很容易求解。 u0 ′ 0 ′ u0 ′ (2) 复验法 (Repeat verification method)先假定一个流型 8

内蒙古农业大学食品科学与工程学院《食品工程原理》讲稿 CH4-§1 区域,选用该区域对应的沉降速度 u0计算式,求得 u0值。由此 u0值 验算雷诺数 Rep,若验算所得 Rep值落在假定区域内,则说明区域假定 正确,计算的 u0 值即为所要求算的沉降速度的最终值。否则,再假 定另一流型区域,重复上述过程,直到验算所得的雷诺数 Rep落在该 假定区域内为止。用复验法最多三次就可得到正确结果。 (3) 直接法(Direct method) 用一个不包含待求量 u0 的无因 次数群 K 来等效地代替雷诺数 Rep作为流型区域判据的作用,可以避 免上述试算过程。 将式(4—8)改写为: ( ) 3 0 4 u d g P ρ ρ ρ ξ − = (4—10) 为消去式(4—10)中待求未知量 u0,将该式两边同乘以 2 2 = µ duρ R ep , 可得另一无因次数群ξ : 2 R ep ( ) 2 2 2 3 4 µ ρ ρ ρ ξ d g R p ep − = (4—11) 因为ξ是 Rep 的函数,所以ξ 也是 Rep 的函数。若令: 2 R ep ( ) 3 1 2 − = µ ρ ρ ρ g K d p (4—12) 则 2 3 3 4 ξR ep = K (4—13) 由于 K 与ξ 之间的关系只差一个常数因子,故 K 也是 Rep的函 数。式(4—12)所表示的不含待求量 u0的无因次数群 K 可作为判别流 2 R ep 9
内蒙古农业大学食品科学与工程学院《食品工程原理》讲稿 CH4-§1 区域,选用该区域对应的沉降速度 u0计算式,求得 u0值。由此 u0值 验算雷诺数 Rep,若验算所得 Rep值落在假定区域内,则说明区域假定 正确,计算的 u0 值即为所要求算的沉降速度的最终值。否则,再假 定另一流型区域,重复上述过程,直到验算所得的雷诺数 Rep落在该 假定区域内为止。用复验法最多三次就可得到正确结果。 (3) 直接法(Direct method) 用一个不包含待求量 u0 的无因 次数群 K 来等效地代替雷诺数 Rep作为流型区域判据的作用,可以避 免上述试算过程。 将式(4—8)改写为: ( ) 3 0 4 u d g P ρ ρ ρ ξ − = (4—10) 为消去式(4—10)中待求未知量 u0,将该式两边同乘以 2 2 = µ duρ R ep , 可得另一无因次数群ξ : 2 R ep ( ) 2 2 2 3 4 µ ρ ρ ρ ξ d g R p ep − = (4—11) 因为ξ是 Rep 的函数,所以ξ 也是 Rep 的函数。若令: 2 R ep ( ) 3 1 2 − = µ ρ ρ ρ g K d p (4—12) 则 2 3 3 4 ξR ep = K (4—13) 由于 K 与ξ 之间的关系只差一个常数因子,故 K 也是 Rep的函 数。式(4—12)所表示的不含待求量 u0的无因次数群 K 可作为判别流 2 R ep 9

内蒙古农业大学食品科学与工程学院《食品工程原理》讲稿 CH4-§1 型区域的新判据。 将式(4—7)所表示的 u0 表达式代入雷诺数表达式中得无因次数 群 K 与雷诺数 Rep之间的关系为: ( ) 18 18 3 2 3 d g K R p ep = − = µ ρ ρ ρ 或 3 18 K = R ep (4—14) 当 Rep=1 时,由上式得 K=2.62。此值为层流区(Stockes 区)的上 限值。同样,应用式(4—9)和 Rep=500 可算得湍流区(Newton 区)的下 限 K 值为 43.6。如此,用 K 值表示的流型区域界限为: K43.6 时为湍流区。 计算沉降速度 u0时,先算出 K 值,由此可直接正确地确定流型 区域及其相应的 u0计算式,避免了繁琐的复验过程。 例 4—1 鲜牛乳中脂肪球的平均直径约为 5μm,20℃时,脂肪球 的密度为 1010kg/m3,脱脂乳的密度为 1035kg/m3 ,粘度为 2.12× 10-3Pa·s 试求脂肪球在脱脂乳中的沉降速度。 〔解〕:假定沉降在过渡区中进行,按该区的 Allen 公式得: 10
内蒙古农业大学食品科学与工程学院《食品工程原理》讲稿 CH4-§1 型区域的新判据。 将式(4—7)所表示的 u0 表达式代入雷诺数表达式中得无因次数 群 K 与雷诺数 Rep之间的关系为: ( ) 18 18 3 2 3 d g K R p ep = − = µ ρ ρ ρ 或 3 18 K = R ep (4—14) 当 Rep=1 时,由上式得 K=2.62。此值为层流区(Stockes 区)的上 限值。同样,应用式(4—9)和 Rep=500 可算得湍流区(Newton 区)的下 限 K 值为 43.6。如此,用 K 值表示的流型区域界限为: K43.6 时为湍流区。 计算沉降速度 u0时,先算出 K 值,由此可直接正确地确定流型 区域及其相应的 u0计算式,避免了繁琐的复验过程。 例 4—1 鲜牛乳中脂肪球的平均直径约为 5μm,20℃时,脂肪球 的密度为 1010kg/m3,脱脂乳的密度为 1035kg/m3 ,粘度为 2.12× 10-3Pa·s 试求脂肪球在脱脂乳中的沉降速度。 〔解〕:假定沉降在过渡区中进行,按该区的 Allen 公式得: 10