
第一章 流体流动
第一章 流体流动

第一节 概 述 一、研究对象 管内流体的流动 流体在管内流动时内部受力情况及机械能的变 化,分析产生变化的原因,并利用相关理论进 行定量计算,为设备选型提供依据。 不可压缩流体:流体的体积不随压力及温度变化,这 种流体称为不可压缩流体。 可压缩流体:流体的体积如果随压力及温度变化,则 称为可压缩流体
第一节 概 述 一、研究对象 管内流体的流动 流体在管内流动时内部受力情况及机械能的变 化,分析产生变化的原因,并利用相关理论进 行定量计算,为设备选型提供依据。 不可压缩流体:流体的体积不随压力及温度变化,这 种流体称为不可压缩流体。 可压缩流体:流体的体积如果随压力及温度变化,则 称为可压缩流体

二、学习目的 1、掌握流体在管内流动时所具有的力学性质——黏 性(粘 性) 2、掌握流体在管内流动时机械能的变化情况——机 械能衡算 3、学会利用上述理论计算——管路计算 掌握:简单管路计算 了解:复杂管路计算
二、学习目的 1、掌握流体在管内流动时所具有的力学性质——黏 性(粘 性) 2、掌握流体在管内流动时机械能的变化情况——机 械能衡算 3、学会利用上述理论计算——管路计算 掌握:简单管路计算 了解:复杂管路计算

第二节 流体静力学方程——静止流体的力学性质 一、几个常用概念 1、密度(ρ): ρ=m / v 单位:Kg/m³ 液体——不可压缩流体 气体——可压缩流体; 混合流体密度的计算 2、比容积(υ):υ=v / m=1/ ρ 单位: m³/Kg 3、比重(d):相对密度,流体在一定温度下的密度与4℃ 水(1000Kg/ m³)的密度之比。 4:压强(Pa)(压力): 单位: Pa=N/m² ; 1Kgf / cm²=9.8N / cm² =9.8×104 Pa; 1atm=760mmHg=1.013×105 Pa 表示方法:表压力;绝对压力;真空度 绝对压力=大气压+表压力 绝对压力=大气压-真空度
第二节 流体静力学方程——静止流体的力学性质 一、几个常用概念 1、密度(ρ): ρ=m / v 单位:Kg/m³ 液体——不可压缩流体 气体——可压缩流体; 混合流体密度的计算 2、比容积(υ):υ=v / m=1/ ρ 单位: m³/Kg 3、比重(d):相对密度,流体在一定温度下的密度与4℃ 水(1000Kg/ m³)的密度之比。 4:压强(Pa)(压力): 单位: Pa=N/m² ; 1Kgf / cm²=9.8N / cm² =9.8×104 Pa; 1atm=760mmHg=1.013×105 Pa 表示方法:表压力;绝对压力;真空度 绝对压力=大气压+表压力 绝对压力=大气压-真空度

表压与真空度的动画
表压与真空度的动画

真空度=当地大气压-系统绝压 =-(系统绝压-当地大气压) =-表压 例如某系统真空度为 200mmHg,当地大气压为 101.3kPa, 则:表压=-真空度=-200/760*101.3=-26.7kPa 系统绝压=表压+当地大气压 表压等于系统绝压减去当地大气压,而真空度是当地大气压减 去系统绝压。真空度正好是负的表压。比如某系统的真空度为 200mmHg,则系统的表压为-200mmHg。如果当地大气压等于 760mmHg,该系统的绝压为,表压加上当地大气压,等于 560mmHg
真空度=当地大气压-系统绝压 =-(系统绝压-当地大气压) =-表压 例如某系统真空度为 200mmHg,当地大气压为 101.3kPa, 则:表压=-真空度=-200/760*101.3=-26.7kPa 系统绝压=表压+当地大气压 表压等于系统绝压减去当地大气压,而真空度是当地大气压减 去系统绝压。真空度正好是负的表压。比如某系统的真空度为 200mmHg,则系统的表压为-200mmHg。如果当地大气压等于 760mmHg,该系统的绝压为,表压加上当地大气压,等于 560mmHg

1[atm] = 101330 Pa = 10.34米水柱=1.033工程大气压= 760 mmHg 空气 1.293 kg m 0.0173cp 3 = = − , 3 0.0173 10− = SI 单位, 1 1 1.01 kJ kg K − − = Cp ,管内流速取 1 8 ~ 15 m s − 水 1000 kg m 1cp 3 = = − , 3 1 10− = SI 单位, 1 1 4.187 kJ kg K − − = Cp , 管内流速取 1 1 ~ 3 m s − 常用数据和单位
1[atm] = 101330 Pa = 10.34米水柱=1.033工程大气压= 760 mmHg 空气 1.293 kg m 0.0173cp 3 = = − , 3 0.0173 10− = SI 单位, 1 1 1.01 kJ kg K − − = Cp ,管内流速取 1 8 ~ 15 m s − 水 1000 kg m 1cp 3 = = − , 3 1 10− = SI 单位, 1 1 4.187 kJ kg K − − = Cp , 管内流速取 1 1 ~ 3 m s − 常用数据和单位
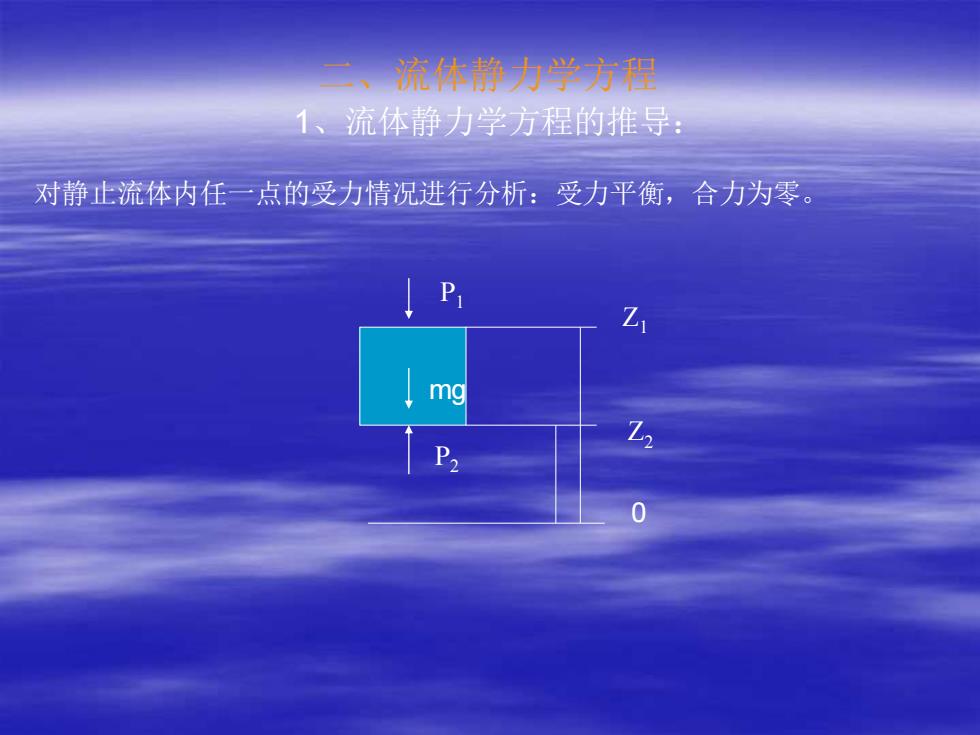
二、流体静力学方程 1、流体静力学方程的推导: 对静止流体内任一点的受力情况进行分析:受力平衡,合力为零。 P1 mg P2 0 Z2 Z1
二、流体静力学方程 1、流体静力学方程的推导: 对静止流体内任一点的受力情况进行分析:受力平衡,合力为零。 P1 mg P2 0 Z2 Z1

设受力向上为正:有 P1 =p1A P2 =p2 A mg=ρVg=ρA(Z1-Z2)g 可得: P2 =P1+ρ(Z1-Z2)g 或 Z1-Z2=(P2-P1)/ρg P1 /ρg+Z1 =P2 /ρg+Z2=常数 讨论: ①流体内任一点压力大小与相邻点压力及流体密度、该点位置有关; ②压力或压差的大小可以用液体的液柱高低表示; ③流体内任一点机械能守恒,P/ρg ——静压头, Z——位压头
设受力向上为正:有 P1 =p1A P2 =p2 A mg=ρVg=ρA(Z1-Z2)g 可得: P2 =P1+ρ(Z1-Z2)g 或 Z1-Z2=(P2-P1)/ρg P1 /ρg+Z1 =P2 /ρg+Z2=常数 讨论: ①流体内任一点压力大小与相邻点压力及流体密度、该点位置有关; ②压力或压差的大小可以用液体的液柱高低表示; ③流体内任一点机械能守恒,P/ρg ——静压头, Z——位压头

2、流体静力学方程的应用: 压力测定 液位高度测定 液封高度测定 仪器——U型管压差计
2、流体静力学方程的应用: 压力测定 液位高度测定 液封高度测定 仪器——U型管压差计