
第四章 传 热
第四章 传 热

第一节 概 述 一、传热的方法 热传导、对流传热、辐射传热 二、学习内容及目的 1、掌握各种传热过程的基本原理 2、掌握总的传热速度方程及其应用计算——传热计算 3、掌握总的传热系数K及传热平均温度差的计算 4、了解对流传热系数的建立及辐射传热的规律
第一节 概 述 一、传热的方法 热传导、对流传热、辐射传热 二、学习内容及目的 1、掌握各种传热过程的基本原理 2、掌握总的传热速度方程及其应用计算——传热计算 3、掌握总的传热系数K及传热平均温度差的计算 4、了解对流传热系数的建立及辐射传热的规律

第二节 热传导 一、傅立叶定律——热传导的基本理论 热传导的定义:依靠物体内自由电子运动或分子原 位振动,从而导致热量的传递,即热传导。 1、几个概念 温度场:一个空间各点温度随时间的分布,称为温 度场。 稳定的温度场:各点温度不随时间变化。 等温面:温度场中,温度相等的点组成的面。(等 温面之间不相交) 温度梯度:温度沿着温度增大方向的变化率。dt/dx
第二节 热传导 一、傅立叶定律——热传导的基本理论 热传导的定义:依靠物体内自由电子运动或分子原 位振动,从而导致热量的传递,即热传导。 1、几个概念 温度场:一个空间各点温度随时间的分布,称为温 度场。 稳定的温度场:各点温度不随时间变化。 等温面:温度场中,温度相等的点组成的面。(等 温面之间不相交) 温度梯度:温度沿着温度增大方向的变化率。dt/dx

W (m ℃) ℃ m dx dt A m Q W − − − − − − − − / / 2 比例系数,称导热系数, 温度梯度, 传热面积, 单位时间传热量, 2、傅立叶定律 dx dt A Q q dx dt Q = −A 或 = = −
W (m ℃) ℃ m dx dt A m Q W − − − − − − − − / / 2 比例系数,称导热系数, 温度梯度, 传热面积, 单位时间传热量, 2、傅立叶定律 dx dt A Q q dx dt Q = −A 或 = = −

二、平壁的稳定热传导——傅立叶定律应用 1、单层平壁 t 0 b ( ) 1 2 t t b A Q dx dt Q A = − = − 积分 x t2 t1
二、平壁的稳定热传导——傅立叶定律应用 1、单层平壁 t 0 b ( ) 1 2 t t b A Q dx dt Q A = − = − 积分 x t2 t1
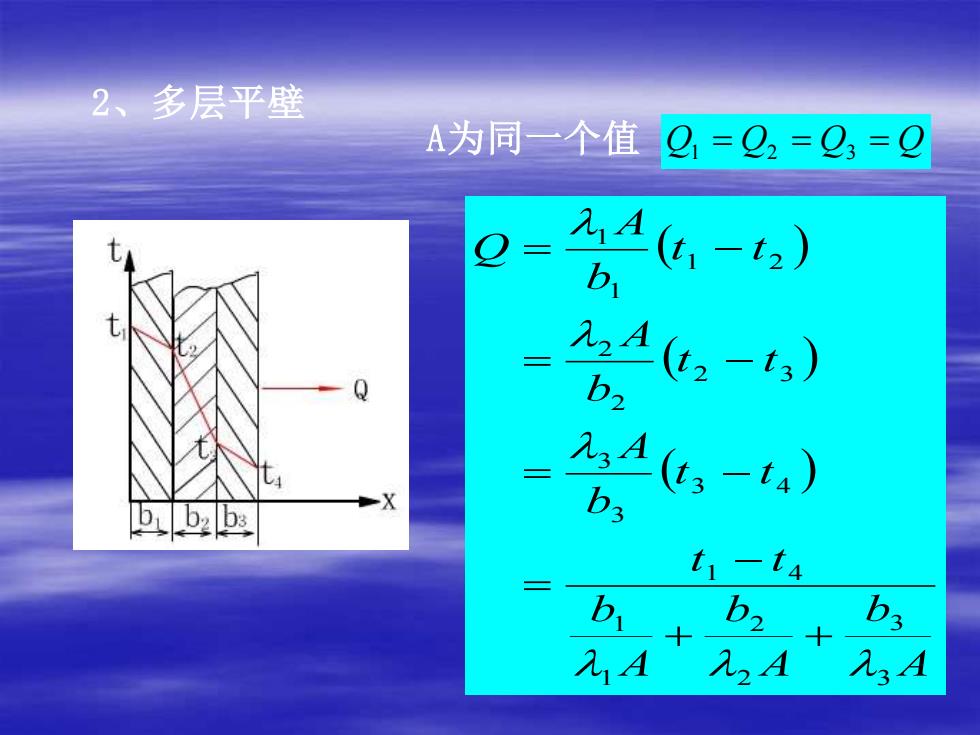
2、多层平壁 A为同一个值 Q 1 = Q 2 = Q 3 = Q ( ) ( ) ( ) A b A b A b t t t t b A t t b A t t b A Q 3 3 22 1 1 1 4 3 4 3 3 2 3 22 1 2 1 1 + + − == − = − = −
2、多层平壁 A为同一个值 Q 1 = Q 2 = Q 3 = Q ( ) ( ) ( ) A b A b A b t t t t b A t t b A t t b A Q 3 3 22 1 1 1 4 3 4 3 3 2 3 22 1 2 1 1 + + − == − = − = −

例4-1 某冷库壁内外层砖壁厚各为12 cm ,中间夹层 填以绝热材料,厚10 cm 。已知砖的导热系数为 0.70 W/ (m·K) ,绝热材料的导热系数为 0.04W/(m·K)。墙的外表面温度为10 ℃ ,内表面温 度为-5℃ 。试计算进入冷库的热流密度及绝热材料与 砖墙两接触面上的温度。 解:根据题意, , ( ), ( ) , , , b m W m K W m K t ℃ t ℃ b b cm m = = = = = = − = = = 0.1 0.7 / 0.04 / 10 5 12 0.12 2 1 3 2 1 4 1 3
例4-1 某冷库壁内外层砖壁厚各为12 cm ,中间夹层 填以绝热材料,厚10 cm 。已知砖的导热系数为 0.70 W/ (m·K) ,绝热材料的导热系数为 0.04W/(m·K)。墙的外表面温度为10 ℃ ,内表面温 度为-5℃ 。试计算进入冷库的热流密度及绝热材料与 砖墙两接触面上的温度。 解:根据题意, , ( ), ( ) , , , b m W m K W m K t ℃ t ℃ b b cm m = = = = = = − = = = 0.1 0.7 / 0.04 / 10 5 12 0.12 2 1 3 2 1 4 1 3

℃ b t q b t t q ℃ b t t q t t W m b b b t t A Q q q 4.1 0.7 0.12 5 5.27 9.1 0.7 0.12 10 5.27 2 5.27 / 0.1 0.12 0.04 0.1 0.7 0.12 10 5 (1) 3 3 4 2 2 3 2 1 1 2 1 2 3 2 3 3 2 2 1 1 1 4 = − = + = − + = − = − = − = = + + − − = + + − = = ( )求 和 ( ) ( ) 求热流密度
℃ b t q b t t q ℃ b t t q t t W m b b b t t A Q q q 4.1 0.7 0.12 5 5.27 9.1 0.7 0.12 10 5.27 2 5.27 / 0.1 0.12 0.04 0.1 0.7 0.12 10 5 (1) 3 3 4 2 2 3 2 1 1 2 1 2 3 2 3 3 2 2 1 1 1 4 = − = + = − + = − = − = − = = + + − − = + + − = = ( )求 和 ( ) ( ) 求热流密度

三、圆筒壁的稳定热传导 1、单层圆筒壁的稳定热传导 比平壁复杂,传热面积 A是个变量。 A = 2rL 对于同一管子,L内外一致,只有r 在变, 如图所示 -圆筒长 -圆筒的内半径 -圆筒的外半径 -圆筒中任意处半径 L r1 r2 r1 r2 r L t2 t1
三、圆筒壁的稳定热传导 1、单层圆筒壁的稳定热传导 比平壁复杂,传热面积 A是个变量。 A = 2rL 对于同一管子,L内外一致,只有r 在变, 如图所示 -圆筒长 -圆筒的内半径 -圆筒的外半径 -圆筒中任意处半径 L r1 r2 r1 r2 r L t2 t1

( )( ) ( ) ( ) ( ) 1 2 1 2 2 1 1 2 2 1 1 2 1 2 1 2 2 ln 2 ln 2 2 t t b A b t t Lr r r r r r r t t L r r t t Q L dr dt rL dr dt Q A m m = − − = − − − = − = = − = − 积分得 1 2 2 1 1 1 2 2 1 2 ln 2 2 2 r r r r > r r r r r r r r m m − = + 当 时, = , 时
( )( ) ( ) ( ) ( ) 1 2 1 2 2 1 1 2 2 1 1 2 1 2 1 2 2 ln 2 ln 2 2 t t b A b t t Lr r r r r r r t t L r r t t Q L dr dt rL dr dt Q A m m = − − = − − − = − = = − = − 积分得 1 2 2 1 1 1 2 2 1 2 ln 2 2 2 r r r r > r r r r r r r r m m − = + 当 时, = , 时