
内蒙古农业大学食品科学与工程系《化工原理》课程讲稿 第一章-§1 第一章 流体流动(Fluid flow) 一、为什么要学习这章?Why should we study the theory of fluid flow? 流体:气体和液体统称为流体。 1. 在化工生产中,所处理的物料有很多是流体。根据生产要求,往往需要 将这些流体按照生产程序从一个设备输送到另一个设备。 2. 除了流体输送外,化工生产中的传热、传质过程以及化学反应大都是在 流动下进行的。流体流动的状态对这些单元操作有着很大影响。为了深入理解 这些单元操作的原理,就必须掌握流体流动的基本原理。可以说流体流动的基 本原理是本课程的重要基础。 二、流体流动的性质 The Features of the fluid flow 1.流体流动是连续的。因为它作为一个整体运动的同时,内部有相对运动。 2.实质:并非指其内部分子的运动(静止流体的分子是运动的),而是由 内部质点的运动来体现。流体内部无数质点运动的总和,就为流体流动。 3.质点及流体流动连续性:指大量分子构成的集团,但其大小与管路线容 器的尺寸相比仍微不足道。因此,可用统计平均方法来思考问题。这样可摆脱 复杂的分子运动从宏观的角度来研究流体的流动规律。 4.不可压缩流体:流体的体积(密度)如果不随压力及温度变化,. 5.可压缩流体:流体的体积(密度)如果随压力及温度变化
内蒙古农业大学食品科学与工程系《化工原理》课程讲稿 第一章-§1 第一章 流体流动(Fluid flow) 一、为什么要学习这章?Why should we study the theory of fluid flow? 流体:气体和液体统称为流体。 1. 在化工生产中,所处理的物料有很多是流体。根据生产要求,往往需要 将这些流体按照生产程序从一个设备输送到另一个设备。 2. 除了流体输送外,化工生产中的传热、传质过程以及化学反应大都是在 流动下进行的。流体流动的状态对这些单元操作有着很大影响。为了深入理解 这些单元操作的原理,就必须掌握流体流动的基本原理。可以说流体流动的基 本原理是本课程的重要基础。 二、流体流动的性质 The Features of the fluid flow 1.流体流动是连续的。因为它作为一个整体运动的同时,内部有相对运动。 2.实质:并非指其内部分子的运动(静止流体的分子是运动的),而是由 内部质点的运动来体现。流体内部无数质点运动的总和,就为流体流动。 3.质点及流体流动连续性:指大量分子构成的集团,但其大小与管路线容 器的尺寸相比仍微不足道。因此,可用统计平均方法来思考问题。这样可摆脱 复杂的分子运动从宏观的角度来研究流体的流动规律。 4.不可压缩流体:流体的体积(密度)如果不随压力及温度变化,. 5.可压缩流体:流体的体积(密度)如果随压力及温度变化

内蒙古农业大学食品科学与工程系《化工原理》课程讲稿 第一章-§1 在研究流体流动时,常将流体视为由无数流体微团组成的连续介质。 所谓流体微团或流体质点是指这样的小块流体:它的大小与容器或管道相比是 微不足道的,但是比起分子自由程长度却要大得多,它包含足够多的分子,能 够用统计平均的方法来求出宏观的参数(如压力、温度),从而使我们可以观察 这些参数的变化情况。连续性的假设首先意味着流体介质是由连续的液体质点 组成的;其次还意味着质点运动过程的连续性。这样就可能在任何情况下都适 用,例如,高度真空下的气体,就不再视为连续性介质了。 流体的体积如果不随压力及温度变化,这种流体称为不可压缩流体;如果随 压力及温度变化,则称为可压缩流体。实际流体都是可压缩的,但由于流体的 体积随压力及温度变化很小,所以一般把它当作不可压缩流体;气体比液体有 较大的压缩性,当压力及温度改变时,气体的体积会有很大的变化,应当属于 可压缩流体。但是,如果压力或温度变化率很小时,气体通常也可以当作不可 压缩流体处理。 第一节 流体静力学基本原理 The Basic Principles of Fliud Statics 1—1 流体的密度和压力 Density and Pressure of Fluid 1.1A 密度 Density 单位体积流体的质量,称为流体的密度,其表达式为 m V ρ = (1—1) 式中 ρ――流体的密度,kg/m3 ;
内蒙古农业大学食品科学与工程系《化工原理》课程讲稿 第一章-§1 在研究流体流动时,常将流体视为由无数流体微团组成的连续介质。 所谓流体微团或流体质点是指这样的小块流体:它的大小与容器或管道相比是 微不足道的,但是比起分子自由程长度却要大得多,它包含足够多的分子,能 够用统计平均的方法来求出宏观的参数(如压力、温度),从而使我们可以观察 这些参数的变化情况。连续性的假设首先意味着流体介质是由连续的液体质点 组成的;其次还意味着质点运动过程的连续性。这样就可能在任何情况下都适 用,例如,高度真空下的气体,就不再视为连续性介质了。 流体的体积如果不随压力及温度变化,这种流体称为不可压缩流体;如果随 压力及温度变化,则称为可压缩流体。实际流体都是可压缩的,但由于流体的 体积随压力及温度变化很小,所以一般把它当作不可压缩流体;气体比液体有 较大的压缩性,当压力及温度改变时,气体的体积会有很大的变化,应当属于 可压缩流体。但是,如果压力或温度变化率很小时,气体通常也可以当作不可 压缩流体处理。 第一节 流体静力学基本原理 The Basic Principles of Fliud Statics 1—1 流体的密度和压力 Density and Pressure of Fluid 1.1A 密度 Density 单位体积流体的质量,称为流体的密度,其表达式为 m V ρ = (1—1) 式中 ρ――流体的密度,kg/m3 ;

内蒙古农业大学食品科学与工程系《化工原理》课程讲稿 第一章-§1 m――流体的质量,kg; V――流体的体积,m3 。 不同的流体密度是不同的,对一定的流体,密度是压力 p 和 T 的函数,可 用下式表示 ρ=f(p,T) 液体的密度随压力的变化甚小(极高压力下除外),可忽略不计,故常称液 体为不可压缩的流体,但其随温度稍有改变。气体的密度随压力和温度的变化 较大,当压力不太高、温度不太低时,气体的密度可近似地按理想气体状态方 程式计算,由 RT M m pV = 得 RT pM V m ρ = = (1—2) 式中 p――气体的压力,kN/m2 或 kPa; T――气体的绝对温度,K; M――气体的分子量,kg/kmol; R――通用气体常数,8.314kJ/kmol·K。 气体密度也可按下式计算 0 0 0 Tp T p ρ = ρ (1—3) 上式中的 ρ0=M/22.4kg/m3 为标准状态(即 T0=273K 及 p0=133.3Pa)下气 体的密度。 在气体压力较高、温度较低时,气体的密度需要采用真实气体状态方程式 计算
内蒙古农业大学食品科学与工程系《化工原理》课程讲稿 第一章-§1 m――流体的质量,kg; V――流体的体积,m3 。 不同的流体密度是不同的,对一定的流体,密度是压力 p 和 T 的函数,可 用下式表示 ρ=f(p,T) 液体的密度随压力的变化甚小(极高压力下除外),可忽略不计,故常称液 体为不可压缩的流体,但其随温度稍有改变。气体的密度随压力和温度的变化 较大,当压力不太高、温度不太低时,气体的密度可近似地按理想气体状态方 程式计算,由 RT M m pV = 得 RT pM V m ρ = = (1—2) 式中 p――气体的压力,kN/m2 或 kPa; T――气体的绝对温度,K; M――气体的分子量,kg/kmol; R――通用气体常数,8.314kJ/kmol·K。 气体密度也可按下式计算 0 0 0 Tp T p ρ = ρ (1—3) 上式中的 ρ0=M/22.4kg/m3 为标准状态(即 T0=273K 及 p0=133.3Pa)下气 体的密度。 在气体压力较高、温度较低时,气体的密度需要采用真实气体状态方程式 计算

内蒙古农业大学食品科学与工程系《化工原理》课程讲稿 第一章-§1 混合气体的密度计算有两种方法: 1. = ∑ (1—4) n m i i y 1 ρ ρ 2. Mm = ∑ Mi yi (1—5) 式中 M1、M2、. Mn――气体混合物各组分的分子量; y1 、y2 、. yn――气体混合物各组分的摩尔分率。 ρ m — — 平均密度 Mm — —平均分子量 气体混合物的组成通常以体积分率表示。对于理想气体,体积分率与摩尔 分率、压力分率是相等的。 液体混合时,体积往往有所改变。若混合前后体积不变,则 1kg 混合液的 体积等于各组分单独存在时的体积之和,则可由下式求出混合液体的密度 ρ m n n m a a a ρ ρ ρ ρ = + +L 2 2 1 1 1 (1—6) 式中 α1、α2、.,αn――液体混合物中各组分的质量分率; ρ1、ρ2、.,ρn――液体混合物中各组分的密度,kg/m3; ρm――液体混合物的平均密度,kg/m3 。 比容 单位质量流体的体积,称为流体的比容,用符号 v 表示,单位为 m3 /kg,则 ρ 1 = = m V v (1—7)
内蒙古农业大学食品科学与工程系《化工原理》课程讲稿 第一章-§1 混合气体的密度计算有两种方法: 1. = ∑ (1—4) n m i i y 1 ρ ρ 2. Mm = ∑ Mi yi (1—5) 式中 M1、M2、. Mn――气体混合物各组分的分子量; y1 、y2 、. yn――气体混合物各组分的摩尔分率。 ρ m — — 平均密度 Mm — —平均分子量 气体混合物的组成通常以体积分率表示。对于理想气体,体积分率与摩尔 分率、压力分率是相等的。 液体混合时,体积往往有所改变。若混合前后体积不变,则 1kg 混合液的 体积等于各组分单独存在时的体积之和,则可由下式求出混合液体的密度 ρ m n n m a a a ρ ρ ρ ρ = + +L 2 2 1 1 1 (1—6) 式中 α1、α2、.,αn――液体混合物中各组分的质量分率; ρ1、ρ2、.,ρn――液体混合物中各组分的密度,kg/m3; ρm――液体混合物的平均密度,kg/m3 。 比容 单位质量流体的体积,称为流体的比容,用符号 v 表示,单位为 m3 /kg,则 ρ 1 = = m V v (1—7)

内蒙古农业大学食品科学与工程系《化工原理》课程讲稿 第一章-§1 亦即流体的比容是密度的倒数。 例 1-1 已知硫酸与水的密度分别为 1830kg/m3 与 998kg/m3 ,试求含硫酸为 60%(质量)的硫酸水溶液,其密度为若干? 解 根据式(1-7) 4 4 7.28 10 (3.28 4) 10 998 0.4 1830 1 0.6 − − = × = + × = + ρ m 3 ρ m = 1370kg / m 例 1-2 已知干空气的组成为:O221%、N278%和 Ar1%(均为体积%)。试求 干空气在压力为 9.81x104 Pa 及温度为 100℃时的密度。 解 首先将摄氏度换算成开尔文 100℃=273+100=373K 再求干空气的平均分子量 Mm =32*0.21+28*0.78+39.9*0.01 =28.96 根据式(1-3),气体的平均密度为 0.916 1.013 10 9.81 10 373 273 22.4 28.96 5 4 0 0 0 = × × = × × = Tp T p ρ m ρ 1.1B 压 力 流体垂直作用于单位面积上的力,称为流体的压强,简称压强。习惯上称
内蒙古农业大学食品科学与工程系《化工原理》课程讲稿 第一章-§1 亦即流体的比容是密度的倒数。 例 1-1 已知硫酸与水的密度分别为 1830kg/m3 与 998kg/m3 ,试求含硫酸为 60%(质量)的硫酸水溶液,其密度为若干? 解 根据式(1-7) 4 4 7.28 10 (3.28 4) 10 998 0.4 1830 1 0.6 − − = × = + × = + ρ m 3 ρ m = 1370kg / m 例 1-2 已知干空气的组成为:O221%、N278%和 Ar1%(均为体积%)。试求 干空气在压力为 9.81x104 Pa 及温度为 100℃时的密度。 解 首先将摄氏度换算成开尔文 100℃=273+100=373K 再求干空气的平均分子量 Mm =32*0.21+28*0.78+39.9*0.01 =28.96 根据式(1-3),气体的平均密度为 0.916 1.013 10 9.81 10 373 273 22.4 28.96 5 4 0 0 0 = × × = × × = Tp T p ρ m ρ 1.1B 压 力 流体垂直作用于单位面积上的力,称为流体的压强,简称压强。习惯上称

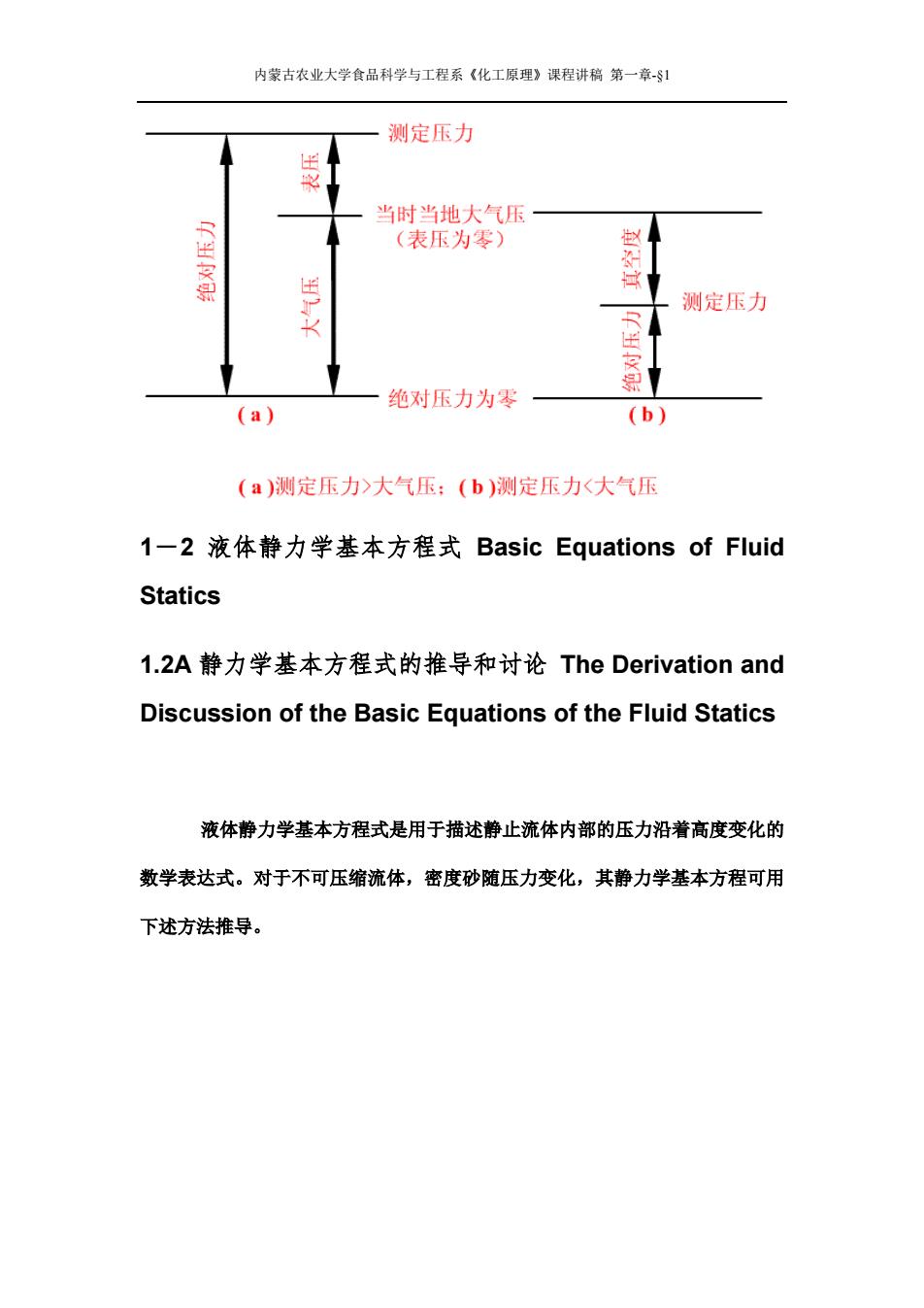
内蒙古农业大学食品科学与工程系《化工原理》课程讲稿 第一章-§1 为压力。作用于整个面上的力称为总压力。在静止流体中,从各方向作用于某 一点的压力大小均相等。 在法定单位制中,压力的单位是 N/m2 ,称为帕斯卡,以 Pa 表示。但长期 以来采用的单位为 atm(标准大气压)、某流体在柱高度、bar(巴)或 kgf/cm2 等。它们之间的换算关系为: 1 标准大气压(atm)=101300Pa =10330kgf/m2 =1.033kgf/cm2 =10.33mH2O =760mmHg 压力可以有不同的计量基准: 如以绝对真空(即零大气压)为基准,称为绝对压力(absolute pressure)。 如以当地大气压为基准,则称为表压(gauge pressure)。 它与绝对压力的关系,可用下式表示 表压=绝对压力-大气压力 (1—9) 当被测流体的绝对压力小于大气压时,其低于大气压的数值称为真空度 (vacuum),即 真空度=大气压力-绝对压力 (1—10) 注意,此处的大气压力均应指当地大气压。在本章中如不加说明时均可按 标准大气压计算。 绝对压力、表压和真空度的关系,如图 1-1 所示。 例 1-3 某台离心泵进、出口压力表读数分别为 220mmHg(真空度)及
内蒙古农业大学食品科学与工程系《化工原理》课程讲稿 第一章-§1 为压力。作用于整个面上的力称为总压力。在静止流体中,从各方向作用于某 一点的压力大小均相等。 在法定单位制中,压力的单位是 N/m2 ,称为帕斯卡,以 Pa 表示。但长期 以来采用的单位为 atm(标准大气压)、某流体在柱高度、bar(巴)或 kgf/cm2 等。它们之间的换算关系为: 1 标准大气压(atm)=101300Pa =10330kgf/m2 =1.033kgf/cm2 =10.33mH2O =760mmHg 压力可以有不同的计量基准: 如以绝对真空(即零大气压)为基准,称为绝对压力(absolute pressure)。 如以当地大气压为基准,则称为表压(gauge pressure)。 它与绝对压力的关系,可用下式表示 表压=绝对压力-大气压力 (1—9) 当被测流体的绝对压力小于大气压时,其低于大气压的数值称为真空度 (vacuum),即 真空度=大气压力-绝对压力 (1—10) 注意,此处的大气压力均应指当地大气压。在本章中如不加说明时均可按 标准大气压计算。 绝对压力、表压和真空度的关系,如图 1-1 所示。 例 1-3 某台离心泵进、出口压力表读数分别为 220mmHg(真空度)及

内蒙古农业大学食品科学与工程系《化工原理》课程讲稿 第一章-§1 1.7kgf/cm2 (表压)。若当地大气压力为 760mmHg,试求它们的绝对压力各为若干 (以法定单位表示)? 解 泵进口绝对压力 P1=760-220=540mmHg =7.2x104 Pa 泵出口绝对压力 P2=1.7+1.033 =2.733kgf/cm2 =2.68x105 Pa
内蒙古农业大学食品科学与工程系《化工原理》课程讲稿 第一章-§1 1.7kgf/cm2 (表压)。若当地大气压力为 760mmHg,试求它们的绝对压力各为若干 (以法定单位表示)? 解 泵进口绝对压力 P1=760-220=540mmHg =7.2x104 Pa 泵出口绝对压力 P2=1.7+1.033 =2.733kgf/cm2 =2.68x105 Pa
内蒙古农业大学食品科学与工程系《化工原理》课程讲稿 第一章-§1 1-2 液体静力学基本方程式 Basic Equations of Fluid Statics 1.2A 静力学基本方程式的推导和讨论 The Derivation and Discussion of the Basic Equations of the Fluid Statics 液体静力学基本方程式是用于描述静止流体内部的压力沿着高度变化的 数学表达式。对于不可压缩流体,密度砂随压力变化,其静力学基本方程可用 下述方法推导
内蒙古农业大学食品科学与工程系《化工原理》课程讲稿 第一章-§1 1-2 液体静力学基本方程式 Basic Equations of Fluid Statics 1.2A 静力学基本方程式的推导和讨论 The Derivation and Discussion of the Basic Equations of the Fluid Statics 液体静力学基本方程式是用于描述静止流体内部的压力沿着高度变化的 数学表达式。对于不可压缩流体,密度砂随压力变化,其静力学基本方程可用 下述方法推导

内蒙古农业大学食品科学与工程系《化工原理》课程讲稿 第一章-§1 现从静止液体中任意划出一垂直液柱,如图 1-2 所示。液柱的横截面积 为 A,液体密度为 ρ,若以容器器底为基准水平面,则液柱的上、下底面与基准 水平面的垂直距离分别为 Z1 和 Z2,以 p1与 p2 分别表示高度为 Z1 及 Z2处的压 力。 在垂直方向上作用于液柱的力有: 下底面所受之向上总压力为 p2A; 上底面所受之向下总压力为 p1A; 整个液柱之 G=ρgA(Z1-Z2)。 在静止液体中,上述三力之合力应为零,即 p2A-p1A-ρgA(Z1-Z2)=0 此式中向上的力用正号,向下的力用负号。化简并消去 A,得 p2=p1+ρg(Z1-Z2) (1-10) 如果将液柱的上底面取在液面上,设液面上方的压力为 p0,液柱 Z1-Z2=h, 则上式可改写为 p2=p0+ρgh (1-11) 式(1-10)及(1-11)称为静力学基本方程式
内蒙古农业大学食品科学与工程系《化工原理》课程讲稿 第一章-§1 现从静止液体中任意划出一垂直液柱,如图 1-2 所示。液柱的横截面积 为 A,液体密度为 ρ,若以容器器底为基准水平面,则液柱的上、下底面与基准 水平面的垂直距离分别为 Z1 和 Z2,以 p1与 p2 分别表示高度为 Z1 及 Z2处的压 力。 在垂直方向上作用于液柱的力有: 下底面所受之向上总压力为 p2A; 上底面所受之向下总压力为 p1A; 整个液柱之 G=ρgA(Z1-Z2)。 在静止液体中,上述三力之合力应为零,即 p2A-p1A-ρgA(Z1-Z2)=0 此式中向上的力用正号,向下的力用负号。化简并消去 A,得 p2=p1+ρg(Z1-Z2) (1-10) 如果将液柱的上底面取在液面上,设液面上方的压力为 p0,液柱 Z1-Z2=h, 则上式可改写为 p2=p0+ρgh (1-11) 式(1-10)及(1-11)称为静力学基本方程式

内蒙古农业大学食品科学与工程系《化工原理》课程讲稿 第一章-§1 将式(1—10)移项得: (1—12) 1 1 2 2 p + ρgz = p + ρgz 式(1—12)各项除以密度 ρ ,可得: 2 2 1 1 gz p gz p + = + ρ ρ (1—13) 式(1—13)各项除以重力加速度 g,可得: 2 2 1 1 z g p z g p + = + ρ ρ (1—14) 讨论: 上述式(1—10) 至。(1—14)为液体静力学基本方程的各种形式。现作如下说 明和讨论: (1)上述流体静力学基本方程各种表达式只适用于重力场中静止的不可 压缩的连续的单一流体。 (2)式(1—11)表明,处于重力场中的流体的静压 p 的大小与流体本身的密度 和垂直位置有关,而与各点的水平位置无关。换句话说,在静止的连续的同 一液体中,处在同一水平位置上 的各点的压力都相等。 ρ 当液面的上方压力 p0 有变化时,必将引起液体内部各点压力发生同样大小 的变化。这就是巴斯噶原理。 (3)式(1—13)中各项的单位是 J/kg,为 1kg 流体具有的能量。其中, ρ p 称 为静压能,gz 为位能。可见,在静止流体中,一处静压能与位能之和等于另一 处静压能与位能之和。静压能和位能都属于机械能。静力学基本方程表明,在 静止流体中,这两种机械能之和是守恒的。 (4)式(1—12)中各项的单位为 Pa,亦即是 J/m3 。各项表示单位体积流体
内蒙古农业大学食品科学与工程系《化工原理》课程讲稿 第一章-§1 将式(1—10)移项得: (1—12) 1 1 2 2 p + ρgz = p + ρgz 式(1—12)各项除以密度 ρ ,可得: 2 2 1 1 gz p gz p + = + ρ ρ (1—13) 式(1—13)各项除以重力加速度 g,可得: 2 2 1 1 z g p z g p + = + ρ ρ (1—14) 讨论: 上述式(1—10) 至。(1—14)为液体静力学基本方程的各种形式。现作如下说 明和讨论: (1)上述流体静力学基本方程各种表达式只适用于重力场中静止的不可 压缩的连续的单一流体。 (2)式(1—11)表明,处于重力场中的流体的静压 p 的大小与流体本身的密度 和垂直位置有关,而与各点的水平位置无关。换句话说,在静止的连续的同 一液体中,处在同一水平位置上 的各点的压力都相等。 ρ 当液面的上方压力 p0 有变化时,必将引起液体内部各点压力发生同样大小 的变化。这就是巴斯噶原理。 (3)式(1—13)中各项的单位是 J/kg,为 1kg 流体具有的能量。其中, ρ p 称 为静压能,gz 为位能。可见,在静止流体中,一处静压能与位能之和等于另一 处静压能与位能之和。静压能和位能都属于机械能。静力学基本方程表明,在 静止流体中,这两种机械能之和是守恒的。 (4)式(1—12)中各项的单位为 Pa,亦即是 J/m3 。各项表示单位体积流体