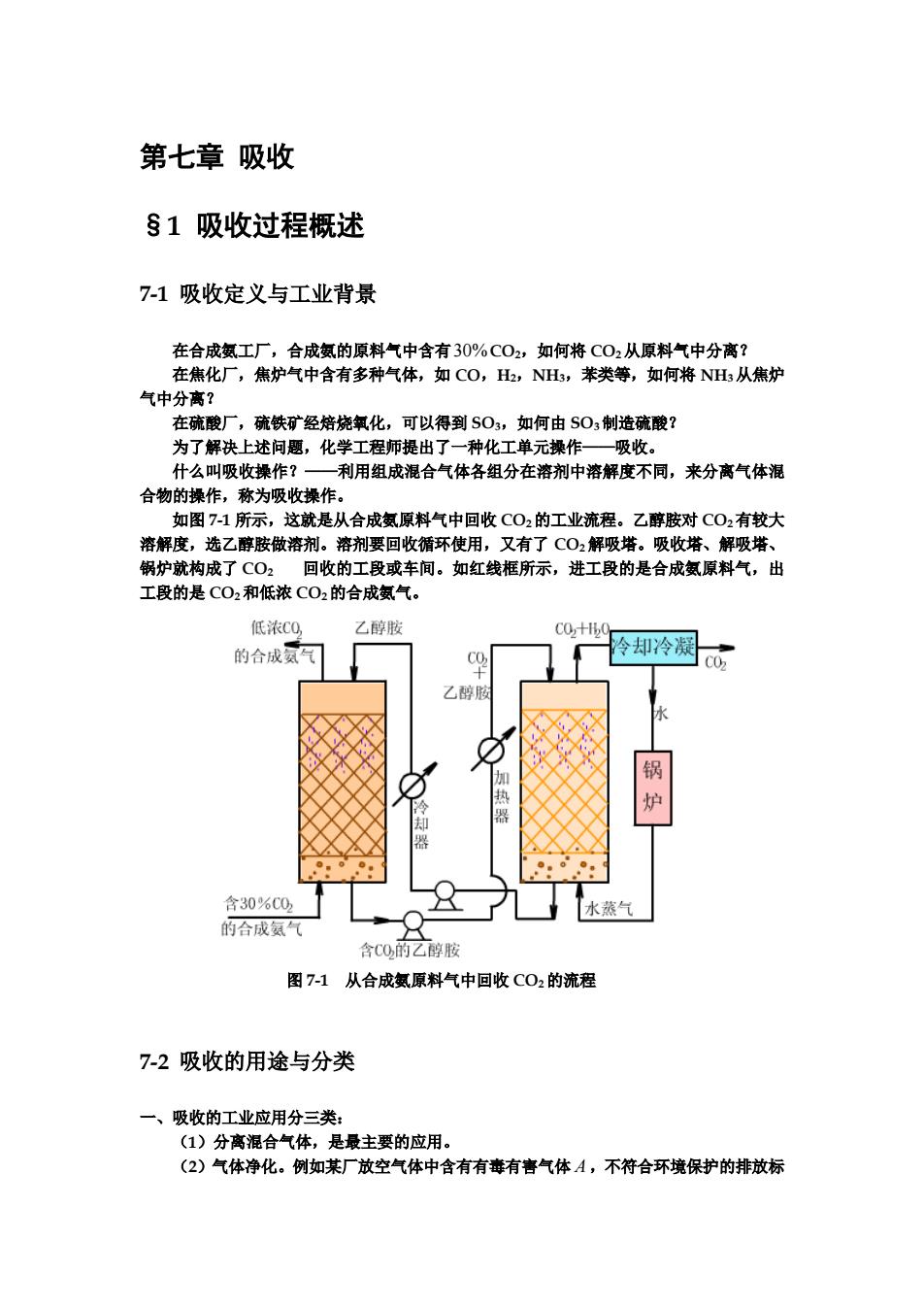
第七章 吸收 §1 吸收过程概述 7-1 吸收定义与工业背景 在合成氨工厂,合成氨的原料气中含有30%CO2,如何将 CO2 从原料气中分离? 在焦化厂,焦炉气中含有多种气体,如 CO,H2,NH3,苯类等,如何将 NH3从焦炉 气中分离? 在硫酸厂,硫铁矿经焙烧氧化,可以得到 SO3,如何由 SO3 制造硫酸? 为了解决上述问题,化学工程师提出了一种化工单元操作——吸收。 什么叫吸收操作?——利用组成混合气体各组分在溶剂中溶解度不同,来分离气体混 合物的操作,称为吸收操作。 如图 7-1 所示,这就是从合成氨原料气中回收 CO2 的工业流程。乙醇胺对 CO2 有较大 溶解度,选乙醇胺做溶剂。溶剂要回收循环使用,又有了 CO2 解吸塔。吸收塔、解吸塔、 锅炉就构成了 CO2 回收的工段或车间。如红线框所示,进工段的是合成氨原料气,出 工段的是 CO2 和低浓 CO2 的合成氨气。 图 7-1 从合成氨原料气中回收 CO2 的流程 7-2 吸收的用途与分类 一、吸收的工业应用分三类: (1)分离混合气体,是最主要的应用。 (2)气体净化。例如某厂放空气体中含有有毒有害气体 A ,不符合环境保护的排放标
第七章 吸收 §1 吸收过程概述 7-1 吸收定义与工业背景 在合成氨工厂,合成氨的原料气中含有30%CO2,如何将 CO2 从原料气中分离? 在焦化厂,焦炉气中含有多种气体,如 CO,H2,NH3,苯类等,如何将 NH3从焦炉 气中分离? 在硫酸厂,硫铁矿经焙烧氧化,可以得到 SO3,如何由 SO3 制造硫酸? 为了解决上述问题,化学工程师提出了一种化工单元操作——吸收。 什么叫吸收操作?——利用组成混合气体各组分在溶剂中溶解度不同,来分离气体混 合物的操作,称为吸收操作。 如图 7-1 所示,这就是从合成氨原料气中回收 CO2 的工业流程。乙醇胺对 CO2 有较大 溶解度,选乙醇胺做溶剂。溶剂要回收循环使用,又有了 CO2 解吸塔。吸收塔、解吸塔、 锅炉就构成了 CO2 回收的工段或车间。如红线框所示,进工段的是合成氨原料气,出 工段的是 CO2 和低浓 CO2 的合成氨气。 图 7-1 从合成氨原料气中回收 CO2 的流程 7-2 吸收的用途与分类 一、吸收的工业应用分三类: (1)分离混合气体,是最主要的应用。 (2)气体净化。例如某厂放空气体中含有有毒有害气体 A ,不符合环境保护的排放标

准,则选用合适溶剂将有害气体吸收,使该厂放空气体达到排放标准。 (3)制备液体产品。例如用水吸收氯化氢气体制备盐酸,用93%硫酸吸收 SO3 制备 硫酸等等。 二、吸收操作工业分类。 按有无化学反应,分物理吸收和化学吸收。例如用 NaOH 吸收 CO2 就是化学吸收。 按溶质气体的数目,分单组分吸收和多组分吸收。 按有无明显热效应,分等温吸收与非等温吸收。 本章重点讨论的是单组分等温的物理吸收。 7-3 吸收计算引论 如图 7-2 所示,填料层高度 Z 与什么有关? 图 7-2 吸收塔示意图 一、首先想到 Z 与分离的物系性质有关。某溶剂对某溶质的溶解度越大,越易吸收,Z 会越小。这与分子间的力有关,即物系的相平衡关系。 二、与传质相界面的面积有关。单位体积填料提供的有效传质面积越大,达到相同分 离要求的 会越小。此即与填料的形状有关。衡量填料形状的因素,可用传质速率与传质 系数表达。 Z 三、若物系相同,填料形状亦相同,但处理的原料气量 和原料气的进出口组成( 和 不同,所以 又与V 有关,此即与物料衡算有关。下面将分相平衡 关系、传质速率、物料衡算等三个方面来展开吸收过程。 (V ) 1 y ) 2 y Z 1 2 1 ,L,y ,y ,x §2 吸收相平衡关系 7-4 气体的溶解度曲线 1.何谓溶解度?——在一定温度与压力下,溶质气体最大限度溶解于溶剂中的量,即溶
准,则选用合适溶剂将有害气体吸收,使该厂放空气体达到排放标准。 (3)制备液体产品。例如用水吸收氯化氢气体制备盐酸,用93%硫酸吸收 SO3 制备 硫酸等等。 二、吸收操作工业分类。 按有无化学反应,分物理吸收和化学吸收。例如用 NaOH 吸收 CO2 就是化学吸收。 按溶质气体的数目,分单组分吸收和多组分吸收。 按有无明显热效应,分等温吸收与非等温吸收。 本章重点讨论的是单组分等温的物理吸收。 7-3 吸收计算引论 如图 7-2 所示,填料层高度 Z 与什么有关? 图 7-2 吸收塔示意图 一、首先想到 Z 与分离的物系性质有关。某溶剂对某溶质的溶解度越大,越易吸收,Z 会越小。这与分子间的力有关,即物系的相平衡关系。 二、与传质相界面的面积有关。单位体积填料提供的有效传质面积越大,达到相同分 离要求的 会越小。此即与填料的形状有关。衡量填料形状的因素,可用传质速率与传质 系数表达。 Z 三、若物系相同,填料形状亦相同,但处理的原料气量 和原料气的进出口组成( 和 不同,所以 又与V 有关,此即与物料衡算有关。下面将分相平衡 关系、传质速率、物料衡算等三个方面来展开吸收过程。 (V ) 1 y ) 2 y Z 1 2 1 ,L,y ,y ,x §2 吸收相平衡关系 7-4 气体的溶解度曲线 1.何谓溶解度?——在一定温度与压力下,溶质气体最大限度溶解于溶剂中的量,即溶
解度。如图 7-3 所示,NH3 溶于水的速率等于 NH3 逸出水的速率,此时达到动平衡。动平 衡时,水中溶解的氨的量,称为在该温度、压力下的氨在水中的溶解度。 图 7-3 气体溶解示意图 2.溶解度曲线——平衡曲线。 若固定温度、压力不变,测得某动平衡下,溶液上方氨的分压为 ,此时溶于水的氨 的浓度为 ;再改变浓度为 ,测得上方氨分压为 ;.依次类推,改变氨的浓度为 , 测得溶液上方氨的分压为 ,如图 7-4 所示。将这 个点,标绘在图上,即得在一定温度、 压力下的溶解度曲线。 1 p 1 x 2 x n 2 p n n x p 图 7-4 实测 p-x 曲线示意图 【例 7-1】 已知 20℃时,在一个大气压下氨气溶解于水的溶解度数据如下表所示,据 此画出的溶解度曲线,横坐标用 x (摩尔分率),纵坐标用 (kPa)。 * p 氨水浓度 kgNH3 100kg水 2 2.5 3 4 5 7.5 10 15 NH3 的平衡分压 mmHg 12 15 18.2 24.9 31.7 50 69.6 114 解:以第六组数据为例计算如下 0.0736 7.5 17 100 18 7.5 17 = + x = p 101.3 6.66 kPa 760 * 50 = × = 将计算结果列在下表中 氨水浓度 x (摩尔分率) 0.0207 0.0258 0.0308 0.0407 0.0503 0.0736 0.0958 0.137
解度。如图 7-3 所示,NH3 溶于水的速率等于 NH3 逸出水的速率,此时达到动平衡。动平 衡时,水中溶解的氨的量,称为在该温度、压力下的氨在水中的溶解度。 图 7-3 气体溶解示意图 2.溶解度曲线——平衡曲线。 若固定温度、压力不变,测得某动平衡下,溶液上方氨的分压为 ,此时溶于水的氨 的浓度为 ;再改变浓度为 ,测得上方氨分压为 ;.依次类推,改变氨的浓度为 , 测得溶液上方氨的分压为 ,如图 7-4 所示。将这 个点,标绘在图上,即得在一定温度、 压力下的溶解度曲线。 1 p 1 x 2 x n 2 p n n x p 图 7-4 实测 p-x 曲线示意图 【例 7-1】 已知 20℃时,在一个大气压下氨气溶解于水的溶解度数据如下表所示,据 此画出的溶解度曲线,横坐标用 x (摩尔分率),纵坐标用 (kPa)。 * p 氨水浓度 kgNH3 100kg水 2 2.5 3 4 5 7.5 10 15 NH3 的平衡分压 mmHg 12 15 18.2 24.9 31.7 50 69.6 114 解:以第六组数据为例计算如下 0.0736 7.5 17 100 18 7.5 17 = + x = p 101.3 6.66 kPa 760 * 50 = × = 将计算结果列在下表中 氨水浓度 x (摩尔分率) 0.0207 0.0258 0.0308 0.0407 0.0503 0.0736 0.0958 0.137
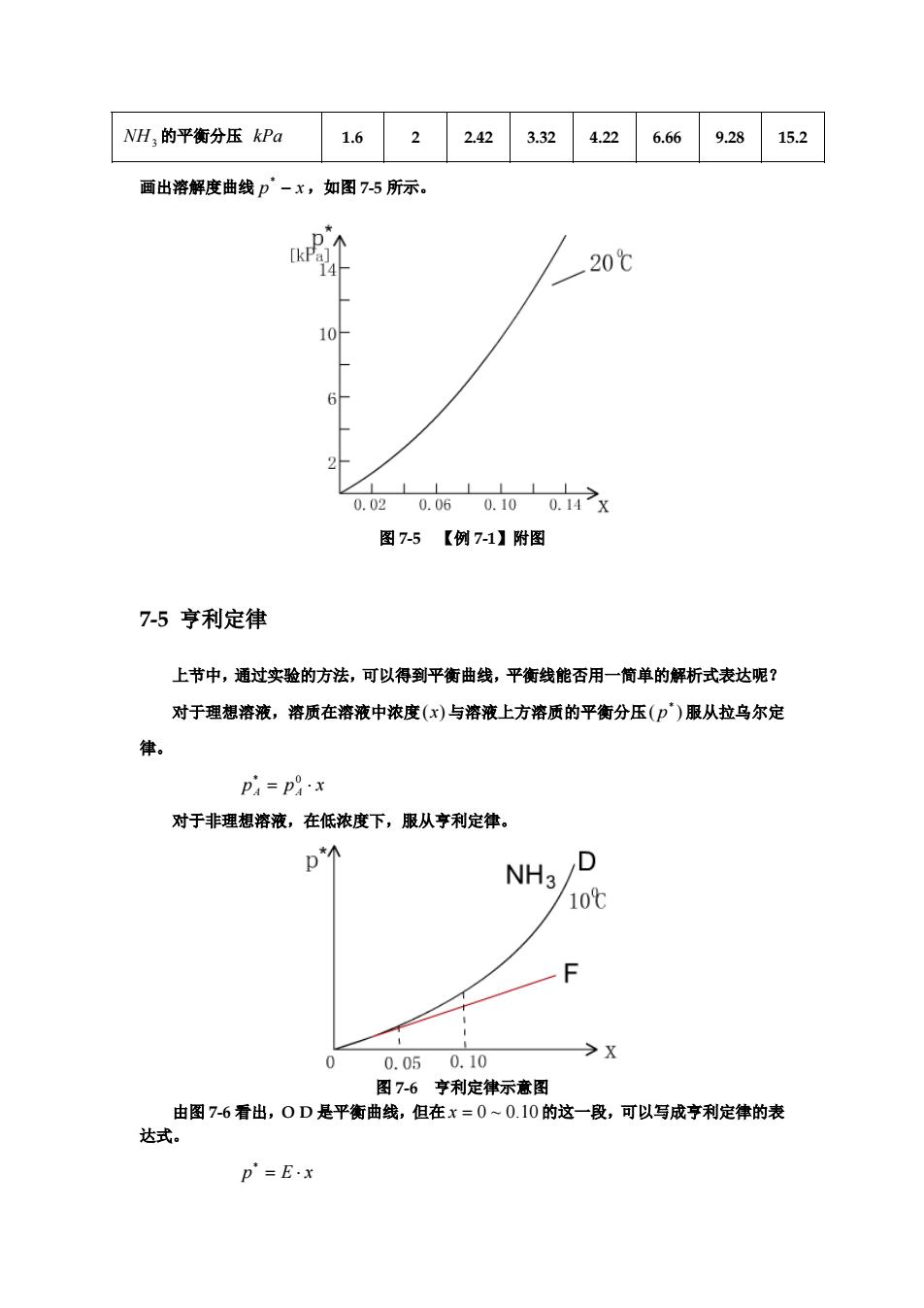
NH3 的平衡分压 kPa 1.6 2 2.42 3.32 4.22 6.66 9.28 15.2 画出溶解度曲线 p − x ,如图 7-5 所示。 * 图 7-5 【例 7-1】附图 7-5 亨利定律 上节中,通过实验的方法,可以得到平衡曲线,平衡线能否用一简单的解析式表达呢? 对于理想溶液,溶质在溶液中浓度 与溶液上方溶质的平衡分压 服从拉乌尔定 律。 (x) ( ) * p p p x A A = ⋅ * 0 对于非理想溶液,在低浓度下,服从亨利定律。 图 7-6 亨利定律示意图 由图 7-6 看出,O D 是平衡曲线,但在 的这一段,可以写成亨利定律的表 达式。 x = 0 ~ 0.10 p = E ⋅ x *
NH3 的平衡分压 kPa 1.6 2 2.42 3.32 4.22 6.66 9.28 15.2 画出溶解度曲线 p − x ,如图 7-5 所示。 * 图 7-5 【例 7-1】附图 7-5 亨利定律 上节中,通过实验的方法,可以得到平衡曲线,平衡线能否用一简单的解析式表达呢? 对于理想溶液,溶质在溶液中浓度 与溶液上方溶质的平衡分压 服从拉乌尔定 律。 (x) ( ) * p p p x A A = ⋅ * 0 对于非理想溶液,在低浓度下,服从亨利定律。 图 7-6 亨利定律示意图 由图 7-6 看出,O D 是平衡曲线,但在 的这一段,可以写成亨利定律的表 达式。 x = 0 ~ 0.10 p = E ⋅ x *

E 称为亨利系数, x 为溶质在溶液中所占的摩尔分率。 亨利定律还可写成: H C p =* 比例系数 愈大,表明同样分压下 的溶解度愈大。 可称为溶解度系数,C 为单 位体积溶液中溶质气体的千摩尔数 kmol·m H * p H -3 亨利定律最常用的是下列形式: y = mx * .(Ⅰ) 式中, ——气相中溶质的摩尔分率; ——液相中溶质的摩尔分率 * y x m ——相平衡常数(亦称亨利常数) 7-6 亨利系数之间的关系 单位: Pa x p E = ⇒ * Pa kmol m p C H 3 * − ⋅ = ⇒ / * = ⇒ x y m 1. E 与 m 的换算 = = y mx p Ex * * m E y p ⇒ = * * .(a) Q 代入式 * * p = P ⋅ y (a) m E y P y = ⋅ ∴ * * P E ⇒ m = 2. E 与 H 的换算 = = H C p p Ex * * H C ⇒ Ex = .(b) ( ) 3 3 1 − − ⋅ + × ⋅ = = kg m kmol kmol M kg kmol kmol m kmol C L m ρ 溶质的 溶剂的 溶质的 溶液的体积 溶质的 数 Mm L x C ρ ∴ =
E 称为亨利系数, x 为溶质在溶液中所占的摩尔分率。 亨利定律还可写成: H C p =* 比例系数 愈大,表明同样分压下 的溶解度愈大。 可称为溶解度系数,C 为单 位体积溶液中溶质气体的千摩尔数 kmol·m H * p H -3 亨利定律最常用的是下列形式: y = mx * .(Ⅰ) 式中, ——气相中溶质的摩尔分率; ——液相中溶质的摩尔分率 * y x m ——相平衡常数(亦称亨利常数) 7-6 亨利系数之间的关系 单位: Pa x p E = ⇒ * Pa kmol m p C H 3 * − ⋅ = ⇒ / * = ⇒ x y m 1. E 与 m 的换算 = = y mx p Ex * * m E y p ⇒ = * * .(a) Q 代入式 * * p = P ⋅ y (a) m E y P y = ⋅ ∴ * * P E ⇒ m = 2. E 与 H 的换算 = = H C p p Ex * * H C ⇒ Ex = .(b) ( ) 3 3 1 − − ⋅ + × ⋅ = = kg m kmol kmol M kg kmol kmol m kmol C L m ρ 溶质的 溶剂的 溶质的 溶液的体积 溶质的 数 Mm L x C ρ ∴ =
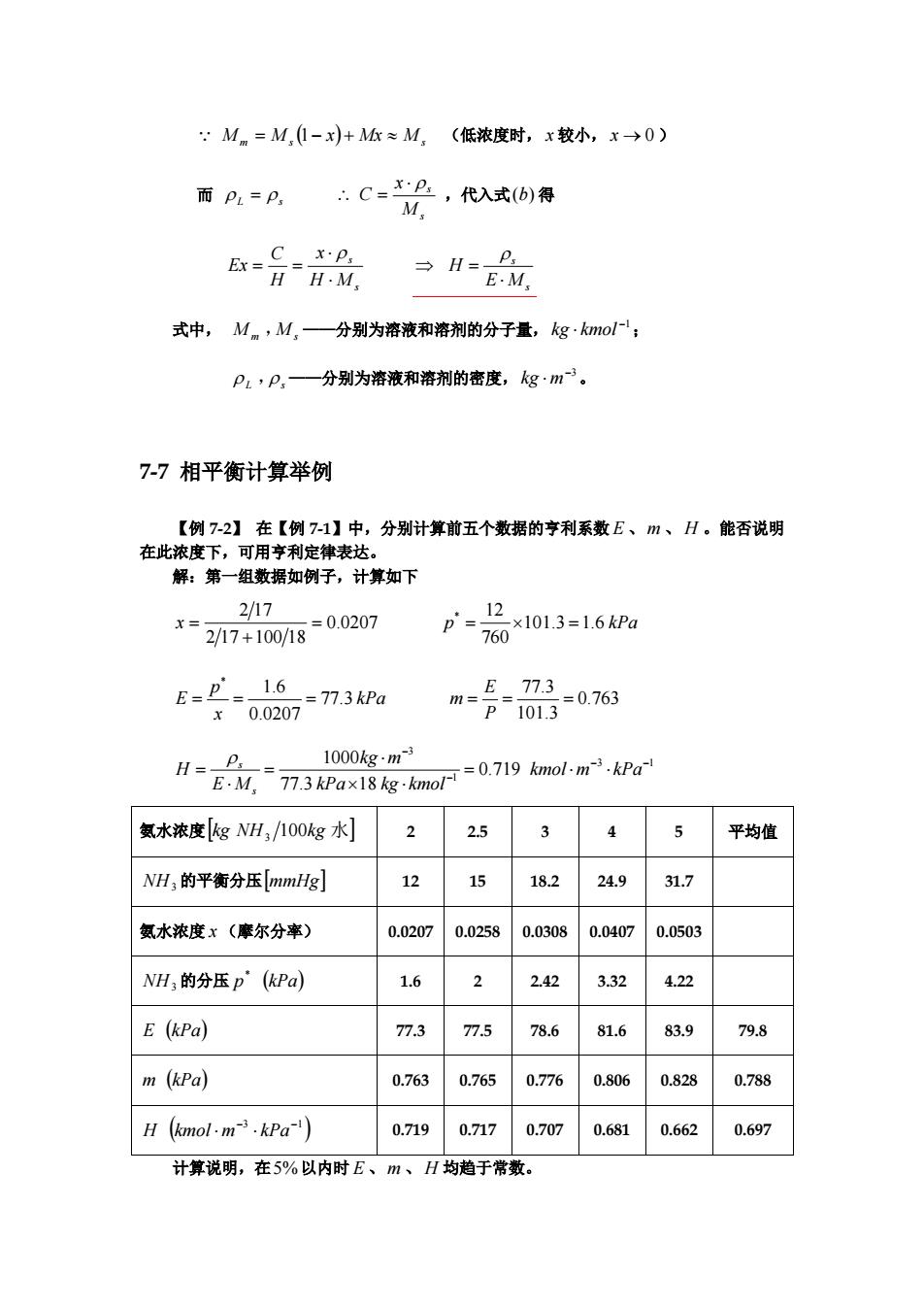
Q M m = M s ( ) 1− x + Mx ≈ M s (低浓度时, x 较小, x → 0 ) 而 ρ L = ρ s s s M x C ⋅ ρ ∴ = ,代入式(b) 得 s s H M x H C Ex ⋅ ⋅ = = ρ s s E M H ⋅ = ρ ⇒ 式中, M m ,M s ——分别为溶液和溶剂的分子量, ;−1 kg ⋅ kmol ρ L ,ρ s ——分别为溶液和溶剂的密度, 。−3 kg ⋅ m 7-7 相平衡计算举例 【例 7-2】 在【例 7-1】中,分别计算前五个数据的亨利系数 、 m 、 。能否说明 在此浓度下,可用亨利定律表达。 E H 解:第一组数据如例子,计算如下 0.0207 2 17 100 18 2 17 = + x = p 101.3 1.6 kPa 760 * 12 = × = kPa x p E 77.3 0.0207 1.6 * = = = 0.763 101.3 77.3 = = = P E m 3 1 1 3 0.719 77.3 18 1000 − − − − = ⋅ ⋅ × ⋅ ⋅ = ⋅ = kmol m kPa kPa kg kmol kg m E M H s ρ s 氨水浓度[kg NH 100kg 水] 3 2 2.5 3 4 5 平均值 NH3 的平衡分压[ ] mmHg 12 15 18.2 24.9 31.7 氨水浓度 x (摩尔分率) 0.0207 0.0258 0.0308 0.0407 0.0503 NH3 的分压 p ( ) kPa * 1.6 2 2.42 3.32 4.22 E ( ) kPa 77.3 77.5 78.6 81.6 83.9 79.8 m ( ) kPa 0.763 0.765 0.776 0.806 0.828 0.788 ( ) −3 −1 H kmol ⋅ m ⋅ kPa 0.719 0.717 0.707 0.681 0.662 0.697 计算说明,在5%以内时 E 、 m 、 H 均趋于常数
Q M m = M s ( ) 1− x + Mx ≈ M s (低浓度时, x 较小, x → 0 ) 而 ρ L = ρ s s s M x C ⋅ ρ ∴ = ,代入式(b) 得 s s H M x H C Ex ⋅ ⋅ = = ρ s s E M H ⋅ = ρ ⇒ 式中, M m ,M s ——分别为溶液和溶剂的分子量, ;−1 kg ⋅ kmol ρ L ,ρ s ——分别为溶液和溶剂的密度, 。−3 kg ⋅ m 7-7 相平衡计算举例 【例 7-2】 在【例 7-1】中,分别计算前五个数据的亨利系数 、 m 、 。能否说明 在此浓度下,可用亨利定律表达。 E H 解:第一组数据如例子,计算如下 0.0207 2 17 100 18 2 17 = + x = p 101.3 1.6 kPa 760 * 12 = × = kPa x p E 77.3 0.0207 1.6 * = = = 0.763 101.3 77.3 = = = P E m 3 1 1 3 0.719 77.3 18 1000 − − − − = ⋅ ⋅ × ⋅ ⋅ = ⋅ = kmol m kPa kPa kg kmol kg m E M H s ρ s 氨水浓度[kg NH 100kg 水] 3 2 2.5 3 4 5 平均值 NH3 的平衡分压[ ] mmHg 12 15 18.2 24.9 31.7 氨水浓度 x (摩尔分率) 0.0207 0.0258 0.0308 0.0407 0.0503 NH3 的分压 p ( ) kPa * 1.6 2 2.42 3.32 4.22 E ( ) kPa 77.3 77.5 78.6 81.6 83.9 79.8 m ( ) kPa 0.763 0.765 0.776 0.806 0.828 0.788 ( ) −3 −1 H kmol ⋅ m ⋅ kPa 0.719 0.717 0.707 0.681 0.662 0.697 计算说明,在5%以内时 E 、 m 、 H 均趋于常数

§3 传质系数与速率方程 7-8 分子扩散与费克定律 (1)分子扩散——流体内某一组分存在浓度差时,则由于分子运动使组分从浓度高处传 递至浓度低处,这种现象称为分子扩散。 (2)费克定律——单位时间通过单位面积物质的扩散量与浓度梯度成正比。 dZ dC J A A ∝ , 写成等式: dZ dC J D A A = − AB 式中, J A ——质量通量 −2 −1 kmol ⋅ m ⋅s dZ dCA ——浓度梯度 4 3 − m ⇒ kmol ⋅ m m kmol DAB —— A 在 B 中的扩散系数 2 −1 m ⋅s 对于气体扩散: = = − = = RT p V n C dZ dC N J D A A A A A A Q dZ dp RT D N A ∴ A = − ∫ ∫ = − i A p p A Z A dp RT D N dZ 0 ( ) A A i p p RT D ⇒ N ⋅ Z = − ( ) A A i p p RTZ D ∴ N = − , Gk RTZ D 令 = —— kG 称为传质系数 ( ) A G A i ∴ N = k p − p 同理,对于液相扩散有: ( ) , A L Ci CA N = k − = Z D k L (3)单相传质的滞流“膜模型
§3 传质系数与速率方程 7-8 分子扩散与费克定律 (1)分子扩散——流体内某一组分存在浓度差时,则由于分子运动使组分从浓度高处传 递至浓度低处,这种现象称为分子扩散。 (2)费克定律——单位时间通过单位面积物质的扩散量与浓度梯度成正比。 dZ dC J A A ∝ , 写成等式: dZ dC J D A A = − AB 式中, J A ——质量通量 −2 −1 kmol ⋅ m ⋅s dZ dCA ——浓度梯度 4 3 − m ⇒ kmol ⋅ m m kmol DAB —— A 在 B 中的扩散系数 2 −1 m ⋅s 对于气体扩散: = = − = = RT p V n C dZ dC N J D A A A A A A Q dZ dp RT D N A ∴ A = − ∫ ∫ = − i A p p A Z A dp RT D N dZ 0 ( ) A A i p p RT D ⇒ N ⋅ Z = − ( ) A A i p p RTZ D ∴ N = − , Gk RTZ D 令 = —— kG 称为传质系数 ( ) A G A i ∴ N = k p − p 同理,对于液相扩散有: ( ) , A L Ci CA N = k − = Z D k L (3)单相传质的滞流“膜模型

图 7-7 单相传质示意图 如图 7-7 所示,萘片的扩散传质,即气相传质,可写成: ( ) G A A A G A A k p p N k p p 1 1 2 1 2 − = − = (传质阻力) (传质推动力) 液相传质可写成: ( ) L A A A L A A k C C N k C C 1 1 2 1 2 − = − = 7-9 两相间传质的“双膜”模型 为了解决多相传质问题,路易斯—惠特曼(Lewis-Whitman)将固体溶解理论引入传 质过程,二十年代提出了双膜模型,其要点如下。 1.两相间有物质传递时,相界面两侧各有一层极薄的静止膜,传递阻力都集中在这里。 这实际上是继承了“滞流膜”模型的观点。例如气—液相间的传质,如图 7-8 所示,气相侧 和液相侧的传质通量分别为: ( ) G A i AG G A i k p p N k p p 1 − = − = .(a) ( ) L i A AL L i A k C C N k C C 1 − = − = .(b) 式中, kG ——以分压差为推动力表示的气相传质分系数, ; −1 −2 −1 kmol ⋅s ⋅ m ⋅ kPa L k ——以浓度差为推动力表示的液相传质分系数, ;−1 m ⋅s A i p 、p ——分别为气相湍流主体和气—液界面上的溶质气体分压, kPa ; CA 、Ci ——分别为液相湍流主体和气—液界面上溶质的液相浓度, 。−3 kmol ⋅ m
图 7-7 单相传质示意图 如图 7-7 所示,萘片的扩散传质,即气相传质,可写成: ( ) G A A A G A A k p p N k p p 1 1 2 1 2 − = − = (传质阻力) (传质推动力) 液相传质可写成: ( ) L A A A L A A k C C N k C C 1 1 2 1 2 − = − = 7-9 两相间传质的“双膜”模型 为了解决多相传质问题,路易斯—惠特曼(Lewis-Whitman)将固体溶解理论引入传 质过程,二十年代提出了双膜模型,其要点如下。 1.两相间有物质传递时,相界面两侧各有一层极薄的静止膜,传递阻力都集中在这里。 这实际上是继承了“滞流膜”模型的观点。例如气—液相间的传质,如图 7-8 所示,气相侧 和液相侧的传质通量分别为: ( ) G A i AG G A i k p p N k p p 1 − = − = .(a) ( ) L i A AL L i A k C C N k C C 1 − = − = .(b) 式中, kG ——以分压差为推动力表示的气相传质分系数, ; −1 −2 −1 kmol ⋅s ⋅ m ⋅ kPa L k ——以浓度差为推动力表示的液相传质分系数, ;−1 m ⋅s A i p 、p ——分别为气相湍流主体和气—液界面上的溶质气体分压, kPa ; CA 、Ci ——分别为液相湍流主体和气—液界面上溶质的液相浓度, 。−3 kmol ⋅ m

图 7-8 双膜模型示意图 2.物质通过双膜的传递过程为稳态过程,没有物质的积累。即 NAG = NAL ,写作, NA = kG ( ) p A − pi = kL (Ci − CA ) .(c) 3.假定气—液界面处无传质阻力,且界面处的气—液组成达于平衡。即 和 在气 —液相平衡线上,写作, i p Ci ( ) .( i Ci p = f d) 若气—液相平衡关系服从亨利(Henry)定律,则式(d) 可写作, H C p i i = 或 y = mx 原则上讲,若已知气、液相传质分系数 和 ,我们便可通过双膜模型导出式 和 式 ,联立求解得到未知的气、液界面组成 和 ,再利用式( 或式( 求得传质通量 。 Gk i p L k Ci (c) (d) A a) b) N 7-10 双膜模型计算举例 【例 7-3】 用水吸收空气中的甲醇蒸汽,温度为 300K 时的 , 气相传质分系数 ,液相传质分系数 k 。 在吸收设 备的某截 面上,气 相主体分 压 ,液相 主 体 浓 度 3 1 2 − − H = kmol ⋅ m ⋅ kPa 1 0.075 − = m ⋅ h L kPa 2 1 1 0.056 − − − k = kmol ⋅ m ⋅ h ⋅ kPa G p A = 2.026
图 7-8 双膜模型示意图 2.物质通过双膜的传递过程为稳态过程,没有物质的积累。即 NAG = NAL ,写作, NA = kG ( ) p A − pi = kL (Ci − CA ) .(c) 3.假定气—液界面处无传质阻力,且界面处的气—液组成达于平衡。即 和 在气 —液相平衡线上,写作, i p Ci ( ) .( i Ci p = f d) 若气—液相平衡关系服从亨利(Henry)定律,则式(d) 可写作, H C p i i = 或 y = mx 原则上讲,若已知气、液相传质分系数 和 ,我们便可通过双膜模型导出式 和 式 ,联立求解得到未知的气、液界面组成 和 ,再利用式( 或式( 求得传质通量 。 Gk i p L k Ci (c) (d) A a) b) N 7-10 双膜模型计算举例 【例 7-3】 用水吸收空气中的甲醇蒸汽,温度为 300K 时的 , 气相传质分系数 ,液相传质分系数 k 。 在吸收设 备的某截 面上,气 相主体分 压 ,液相 主 体 浓 度 3 1 2 − − H = kmol ⋅ m ⋅ kPa 1 0.075 − = m ⋅ h L kPa 2 1 1 0.056 − − − k = kmol ⋅ m ⋅ h ⋅ kPa G p A = 2.026

3 1.2 − CA = kmol ⋅ m A N = k ,求此时该截面上的传质通量。 A p N = A H ∴ N = = k H NA A G N = k p G i k k p = − pi = f C 解: ( ) ( G A i L Ci CA p − p = k − ) L i A G A i k C C k p 1 1 − = − ∴ H C p i 而 i = L i A G A i k H p C k H p H p 1 ⋅ − = ⋅ − ⋅ 由合比定律得: 2 1 0.1274 0.075 1 0.056 2 2 2.026 1.2 1 − − = ⋅ ⋅ + × − = + ⋅ − kmol m h k H p C G L A A 7-11 传质速率方程 根据双膜理论,两膜内的传质为稳态过程,则有 ( ) ( A i L Ci CA − p = k − ) A A G L i L C p k k ∴ C + + .(a) 由于假定在相界上,气液达到平衡得: ( )i .(b) 可用图解法,由式(a)、(b) 求得 pi 和Ci ,如图 7-9 所示。 图 7-9 双膜理论求界面浓度
3 1.2 − CA = kmol ⋅ m A N = k ,求此时该截面上的传质通量。 A p N = A H ∴ N = = k H NA A G N = k p G i k k p = − pi = f C 解: ( ) ( G A i L Ci CA p − p = k − ) L i A G A i k C C k p 1 1 − = − ∴ H C p i 而 i = L i A G A i k H p C k H p H p 1 ⋅ − = ⋅ − ⋅ 由合比定律得: 2 1 0.1274 0.075 1 0.056 2 2 2.026 1.2 1 − − = ⋅ ⋅ + × − = + ⋅ − kmol m h k H p C G L A A 7-11 传质速率方程 根据双膜理论,两膜内的传质为稳态过程,则有 ( ) ( A i L Ci CA − p = k − ) A A G L i L C p k k ∴ C + + .(a) 由于假定在相界上,气液达到平衡得: ( )i .(b) 可用图解法,由式(a)、(b) 求得 pi 和Ci ,如图 7-9 所示。 图 7-9 双膜理论求界面浓度