北京化工大学2001-2002学年第一学期 《计算化学》期末试卷答案 A 1.计算原理(化学原理和计算方法)(20分) 化学反应速率方程:v=-dc=kC d 式中,V为化学反应速率,c为反应物浓度,1为时间,n为反应级数 k为反应速率常数,dcd!为反应物浓度随时间的变化率。 两边取对数:av=(-当=ln+nlnc 将实验所测得不同时间:的反应物浓度c数据通过插值和差商法求出反应速率V。计算 lny和lnc后,用线性回归子程序计算反应级数n和反应速率常数k。 2.程序框图(30分) 开始 输入:数据点数N, 反应温度TO, 时间间隔王 时间t与浓度c的实验数据T①,C① X()-TD.Y()-C0)(=1.N) 调用中心差商子程序计算反应速率R(w)(de/dr) X①=nTC1,Y=Hn-R】I=1,N) 调用线性回归子程序计算A,B (反应级数S-B,速率常数KS=EXP(A)N) 输出:AB,S,KS 结束
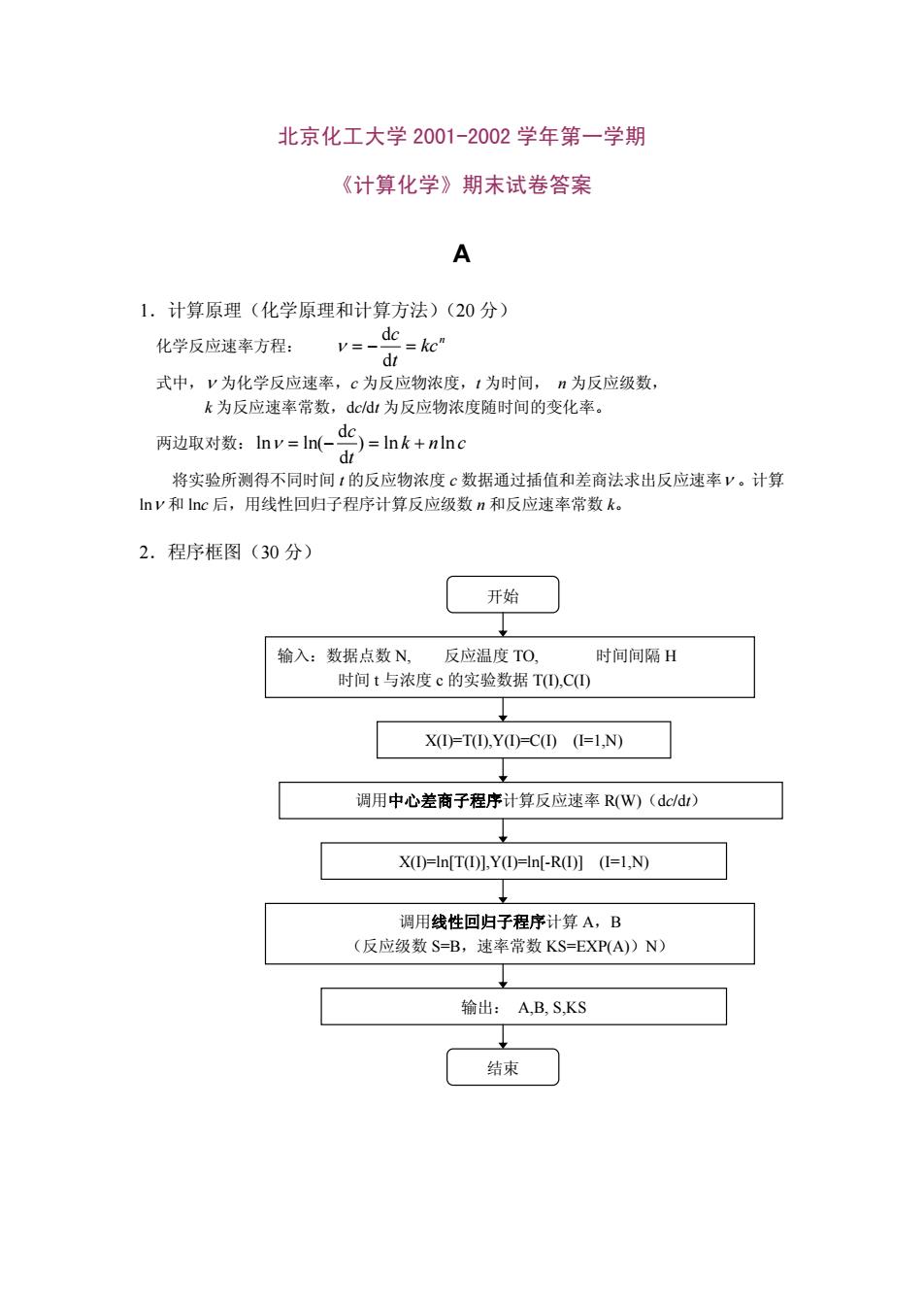
北京化工大学 2001-2002 学年第一学期 《计算化学》期末试卷答案 A 1.计算原理(化学原理和计算方法)(20 分) 化学反应速率方程: n kc t c = − = d d ν 上式中,ν 为化学反应速率,c 为反应物浓度,t 为时间, n 为反应级数, k 为反应速率常数,dc/dt 为反应物浓度随时间的变化率。 上两边取对数: k n c t c ) ln ln d d lnν = ln(− = + 将实验所测得不同时间 t 的反应物浓度 c 数据通过插值和差商法求出反应速率ν 。计算 lnν 和 lnc 后,用线性回归子程序计算反应级数 n 和反应速率常数 k。 2.程序框图(30 分) 开始 输入:数据点数 N, 反应温度 TO, 时间间隔 H 时间 t 与浓度 c 的实验数据 T(I),C(I) (I=1,N) X(I)=T(I),Y(I)=C(I) (I=1,N) 调用中心差商子程序计算反应速率 R(W)(dc/dt) X(I)=ln[T(I)],Y(I)=ln[-R(I)] (I=1,N) 调用线性回归子程序计算 A,B (反应级数 S=B,速率常数 KS=EXP(A))N) 输出: A,B, S,KS 结束

3.源程序(30分) PROGRAM MAIN .VH.A.B.R.S.SS OPEN(6.FILE-TESTA.DAT STATUS-UNKNOWN) N=9 H=10E.5 DATA X/0100200300400500600700800 DATA Y0.05,0.0355,0.0275.,0.0225,0.0185,0.0160,0.0148.& 0.0140.0.0130 CALL CFON.H.X.YV) DO 100ILN XOLOGOYOD Y(D)-LOG(ABS(V(D)) 100 CONTINUE CALL PK(N.X.YA.B.R) S=B SS=EXP(A) WRITE(6.11)A.B.R.S.SS 11 FORMAT(/5X'A=,D18.105XB=,D18.10,5X'R=D18.10M& 5X'n=,D18.10,5Xk=D18.10/0 END SUBROUTINE CFON.H.X.Y.Z DIMENSION X(N).Y(N)Z(N) DOUBLE PRECISION X,Y.Z,H,T,YA,YB T=X(1)+H CALLLGRG2(X,Y.N.T.YA) T=X114)*H CALLLGRG2(X.Y.N.T.YB) Z(D=(4*YA-3*Y(I)-YBX(2*H D010I=2.N-1 T=XO-H CALL LGRG2X.Y.N.TYA) T=X(D+H CALLLGRG2(X.Y.N.T.YB) Z(IH(YB-YAM2H) 10 CONTINUE T=XONLH CALLLGRG2(X.Y.N.T.YA) T-X(N)-2*H CALLLGRG2(X.Y.N,TYB) Z(N(3*Y(N)4*YA+YBM(2*H) RETURN
3.源程序(30 分) PROGRAM MAIN DIMENSION X(9),Y(9),V(9) DOUBLE PRECISION X,Y,V,H,A,B,R,S,SS OPEN(6,FILE='TESTA.DAT',STATUS='UNKNOWN') N=9 H=1.0E-5 DATA X/0,100,200,300,400,500,600,700,800/ DATA Y/0.05,0.0355,0.0275,0.0225,0.0185,0.0160,0.0148, & 0.0140,0.0130/ CALL CF(N,H,X,Y,V) DO 100 I=1,N X(I)=LOG(Y(I)) Y(I)=LOG(ABS(V(I))) 100 CONTINUE CALL PK(N,X,Y,A,B,R) S=B SS=EXP(A) WRITE(6,11)A,B,R,S,SS 11 FORMAT(/5X,'A=',D18.10//5X,'B=',D18.10, 5X,'R=',D18.10// & 5X,'n=',D18.10,5X,'k=',D18.10/) END SUBROUTINE CF(N,H,X,Y,Z) DIMENSION X(N),Y(N),Z(N) DOUBLE PRECISION X,Y,Z,H,T,YA,YB T=X(1)+H CALL LGRG2(X,Y,N,T,YA) T=X(1)+2*H CALL LGRG2(X,Y,N,T,YB) Z(1)=(4*YA-3*Y(1)-YB)/(2*H) DO 10 I=2,N-1 T=X(I)-H CALL LGRG2(X,Y,N,T,YA) T=X(I)+H CALL LGRG2(X,Y,N,T,YB) Z(I)=(YB-YA)/(2*H) 10 CONTINUE T=X(N)-H CALL LGRG2(X,Y,N,T,YA) T=X(N)-2*H CALL LGRG2(X,Y,N,T,YB) Z(N)=(3*Y(N)-4*YA+YB)/(2*H) RETURN

END SUBROUTINEPK(N.X,Y.A.B.R) DOUBLE PRECISION X,Y,A,B,R DIMENSION XON)YON) 8X=00 SY=0.0 SXX-00 SYY-0.0 SXY-0.0 D010=1,N X1=X0 YI-YO) SX-SX+XI SY-SY+YI SXX-SXX+X1*XI SVV=SYY+YIYI SXY-SXY+X1*Yl 10 CONTINUE DXX=SXX -SX*SX/N DYY=SYY-SY*SY/N DXY-SXY-SX+SY/N B=DXY/DXX RETURN END SUBROUTINE LGRG2(X,Y.N,T.Z) DIMENSION X(N),Y(N) DOUBLE PRECISION X,Y,T.Z,S Z=0.0 IF(N.LE.0)RETURN IFON EO DTHEN Z=Y(1) RETURN END IF IF(N.EQ.2)THEN Z=Y(1)*(T-X(2)-Y(2)*(TX1))/X1-X(2) RETURN END IF IF(T.LE.X(2))THEN K=1 M=3
END SUBROUTINE PK(N,X,Y,A,B,R) DOUBLE PRECISION X,Y,A,B,R DIMENSION X(N),Y(N) SX=0.0 SY=0.0 SXX=0.0 SYY=0.0 SXY=0.0 DO 10 I=1,N X1=X(I) Y1=Y(I) SX=SX+X1 SY=SY+Y1 SXX=SXX+X1*X1 SYY=SYY+Y1*Y1 SXY=SXY+X1*Y1 10 CONTINUE DXX=SXX-SX*SX/N DYY=SYY-SY*SY/N DXY=SXY-SX*SY/N B=DXY/DXX A=(SY-B*SX)/N R=DXY/SQRT(DXX*DYY) RETURN END SUBROUTINE LGRG2(X,Y,N,T,Z) DIMENSION X(N),Y(N) DOUBLE PRECISION X,Y,T,Z,S Z=0.0 IF(N.LE.0)RETURN IF(N.EQ.1)THEN Z=Y(1) RETURN END IF IF(N.EQ.2)THEN Z=(Y(1)*(T-X(2))-Y(2)*(T-X(1)))/(X(1)-X(2)) RETURN END IF IF(T.LE.X(2))THEN K=1 M=3

ELSE IF(T.GE.X(N-1))THEN K=N.2 M-N ELSE K=1 M=N 10 IF(IABS(K-M).NE.1)THEN L=K+M0/2 IF(T.LTX(L))THEN ELSE K=L EnDIf G0T010 END IF IF(ABS(T-X(K))LT.ABS(T-X(M)))THEN K=K-1 ELSE M-M+1 END IF END IF Z=0.0 DO30I=K.M S=10 DO20J=K.M IF(J.NE.I)YTHEN S=S*(T-X()V(X(1-X()) END IF CONTINUE Z=Z+S*Y(I) 30 CONTINUE RETURN END 4.运行结果。(20分) A -1479000221D+01 B= 2303009515D+0 .9756013465D+00 n 2303009515D+01 k= .2278653895D+00 动力学方程式为: vs、de 2303009515D+01 2278653895D+00
ELSE IF(T.GE.X(N-1))THEN K=N-2 M=N ELSE K=1 M=N 10 IF(IABS(K-M).NE.1)THEN L=(K+M)/2 IF(T.LT.X(L))THEN M=L ELSE K=L ENDIF GOTO 10 END IF IF(ABS(T-X(K)).LT.ABS(T-X(M))) THEN K=K-1 ELSE M=M+1 END IF END IF Z=0.0 DO 30 I=K,M S=1.0 DO 20 J=K,M IF(J.NE.I)THEN S=S*(T-X(J))/(X(I)-X(J)) END IF 20 CONTINUE Z=Z+S*Y(I) 30 CONTINUE RETURN END 4.运行结果。(20 分) A= -.1479000221D+01 B= .2303009515D+01 R= .9756013465D+00 n= .2303009515D+01 k= .2278653895D+00 动力学方程式为: n kc t c = − = d d ν (n= .2303009515D+01 k= .2278653895D+00)

1.计算原理(化学原理和计算方法)(20分) 色谱分析 4日 离过程 它根据不同组分在相对运动、相互不溶的两相 (流动相和固定相)构成的体系中,组分随流动相运动,并在两相间反复多次的 分配,由于其吸附能力、分配系数、离子交换能力、亲和力或分子大小等性质上 的微小差别而在移动速度上产生大的差异,从而使各组分达到完全分离。 在色谱图上,色谱峰的面积与色谱分析中各物质的含量成正比。此题中已知 A、B物质的峰高数据, 可根据离散点求积的方法即:用Simpson求积方法(其 中调用Lagrange插值法子程序计算任意点的函数值)计算两物质的峰面积,通 过峰面积的比求出物质的含量比。 2.程序框图(30分) 开始 输入:A、B两物质的时间X与浓度峰高Y的实验数据 X(D),Y(I)XIO),YI( 输入:A、B两物质和积分上、下限A,BA1,B1 两次调用Simpson积分法子程序计算A,B物质的峰面积S,S1 (其中调用Lagrange插值法子程序计算任意点的函数值) 计算A,B物质的相对含量之比S/S 输出:S/S1 结束 3源程序(30分) PROGRAM MAIN DOUBLEPRECISIONEPS.A.B.X.Y.A1.B1X1.Y1.S.S1.SS DIMENSION X(10),Y(10),XI(7),YI(7) OPEN(6,FILE-TESTB.DAT.STATUS-UNKNOWN) N=10 M=7 EPS=1.0E-5 DATA X/38,40,53,64,75,86,97,108,119,130/ DATA Y/0,3,17,40,69,90,68,43,19,4/
B 1.计算原理(化学原理和计算方法)(20 分) 色谱分析法是一个分离过程,它根据不同组分在相对运动、相互不溶的两相 (流动相和固定相)构成的体系中,组分随流动相运动,并在两相间反复多次的 分配,由于其吸附能力、分配系数、离子交换能力、亲和力或分子大小等性质上 的微小差别而在移动速度上产生大的差异,从而使各组分达到完全分离。 在色谱图上,色谱峰的面积与色谱分析中各物质的含量成正比。此题中已知 A、B 物质的峰高数据,可根据离散点求积的方法即:用 Simpson 求积方法(其 中调用 Lagrange 插值法子程序计算任意点的函数值)计算两物质的峰面积,通 过峰面积的比求出物质的含量比。 2.程序框图(30 分) 3.源程序(30 分) PROGRAM MAIN DOUBLE PRECISION EPS,A,B,X,Y,A1,B1,X1,Y1,S,S1,SS DIMENSION X(10),Y(10),X1(7),Y1(7) OPEN(6,FILE='TESTB.DAT',STATUS='UNKNOWN') N=10 M=7 EPS=1.0E-5 DATA X/38,40,53,64,75,86,97,108,119,130/ DATA Y/0,3,17,40,69,90,68,43,19,4/ 开始 输入:A、B 两物质的时间 X 与浓度峰高 Y 的实验数据 X(I),Y(I) X1(I),Y1(I) (I=1,N) 输入:A、B 两物质和积分上、下限 A,B A1,B1 两次调用 Simpson 积分法子程序计算 A,B 物质的峰面积 S,S1 (其中调用 Lagrange 插值法子程序计算任意点的函数值) 计算 A,B 物质的相对含量之比 S/S1 输出:S/S1 结束

DATA X1/250,258.266.274,282.290,298/ DATA Y1/0.5,6,14,21,13,5,0/ A1=250 B1=298 CALLSIMP(N.A.B.X.Y.EPS.S) CALLSIMP(M.A1.B1.X1,Y1.EPS.S1) SS-S/S1 WRITE(6,*YS=,S, s1,S1 WRITE(6,11)SS 11 FORMAT(2X,The ratio of content of the two substances(S/S1)is:'F18.10) END SUBROUTINESIMP(M.A.B.X.Y.EPS.S2) DOUBLE PRECISION A.B.X.YEPS S2.FA.FB.XO.YO DIMENSION X(M).Y(M) H=B-A N=1 CALLLGRG2(X.Y.M.A.FA) CALL LGRG2(X.Y.M.B.FBY T1-0.5*H(FA+FB) 10 S=0 D020K=1N +(K-0)H CALLLGRG2(X,Y.M.X0,Y0) 20 S=S+Y0 T2=0.5*T1+H*S) S2=T2+T2-T1V3.0 IF(N.EQ.1)GOTO40 30 D=ABS(S2-SI) IF(ABS(S2).GT.1.0)THEN D=ABS((S2-S1S2) ENDIE IF(D LT EPSIGOTO 50 40 N-N+N H=0.5*H T1=T2 S1=82 G0T010 50 RETURN END SUBROUTINE LGRG2(X,Y.N,T.Z)
DATA X1/250,258,266,274,282,290,298/ DATA Y1/0.5,6,14,21,13,5,0/ A=38 B=130 A1=250 B1=298 CALL SIMP(N,A,B,X,Y,EPS,S) CALL SIMP(M,A1,B1,X1,Y1,EPS,S1) SS=S/S1 WRITE(6,*)'S=',S,' S1=',S1 WRITE(6,11)SS 11 FORMAT(2X,'The ratio of content of the two substances(S/S1) is:',F18.10) END SUBROUTINE SIMP(M,A,B,X,Y,EPS,S2) DOUBLE PRECISION A,B,X,Y,EPS,S2,FA,FB,X0,Y0 DIMENSION X(M),Y(M) H=B-A N=1 CALL LGRG2(X,Y,M,A,FA) CALL LGRG2(X,Y,M,B,FB) T1=0.5*H*(FA+FB) 10 S=0 DO 20 K=1,N X0=A+(K-0.5)*H CALL LGRG2(X,Y,M,X0,Y0) 20 S=S+Y0 T2=0.5*(T1+H*S) S2=T2+(T2-T1)/3.0 IF(N.EQ.1)GOTO 40 30 D=ABS(S2-S1) IF(ABS(S2).GT.1.0)THEN D=ABS((S2-S1)/S2) END IF IF(D.LT.EPS)GOTO 50 40 N=N+N H=0.5*H T1=T2 S1=S2 GOTO 10 50 RETURN END SUBROUTINE LGRG2(X,Y,N,T,Z)

DIMENSION XONYON) DOUBLE PRECISION X.Y.T.Z.S Z-0.0 IF(N.LE.0)RETURN IF(N.EQ.1)THEN 7=Y1) Return ENDIE IF(N.EQ.2)THEN Z(Y(1)*(T-X(2)》Y(2)*(T-X(1))MX(1→X2》 RETURN END IF IF(T.LE.X(2))THEN M=3 ELSE IF(T.GE.X(N-I))THEN K=N-2 M=N ELSE K= M=N 10 IF(IABS(K-M).NE.1)THEN L=(K+MV2 IF(T.LT.X(L)THEN ELSE K ENDIE G0T010 ENDIF IF(ABS(T-X(K)).LT.ABS(T-X(M)))THEN K=K-1 ELse M=M+1 Z=0.0 DO30 I=K.M 9=10 DO 20I=K M IFU.NE.I)THEN S=S*(T-X(J)/XI-XJ)】 END IF 20 CONTINUE
DIMENSION X(N),Y(N) DOUBLE PRECISION X,Y,T,Z,S Z=0.0 IF(N.LE.0)RETURN IF(N.EQ.1)THEN Z=Y(1) RETURN END IF IF(N.EQ.2)THEN Z=(Y(1)*(T-X(2))-Y(2)*(T-X(1)))/(X(1)-X(2)) RETURN END IF IF(T.LE.X(2))THEN K=1 M=3 ELSE IF(T.GE.X(N-1))THEN K=N-2 M=N ELSE K=1 M=N 10 IF(IABS(K-M).NE.1)THEN L=(K+M)/2 IF(T.LT.X(L))THEN M=L ELSE K=L ENDIF GOTO 10 END IF IF(ABS(T-X(K)).LT.ABS(T-X(M))) THEN K=K-1 ELSE M=M+1 END IF END IF Z=0.0 DO 30 I=K,M S=1.0 DO 20 J=K,M IF(J.NE.I)THEN S=S*(T-X(J))/(X(I)-X(J)) END IF 20 CONTINUE
Z=Z+S*Y④ 30 CONTINUE ETURN END 4.运行结果。(20分) S=3890.804468790690000 S1= 479.166938781738300 The ratio of content of the two substances(S/S1)is: 81199351497 (A/B) C 1.计算原理(化学原理和计算方法)(20分) 反应 其动力学方程式为: d[A]--k,[A]+k:[B] dr d[B =k [A]-k2 [B]-k;[B] dIC]=k[B] dr 利用Runge-Kuta法解此方程组,可得不同时刻的[A,B],[C]值。 2.程序框图(30分) 开始 输入:「A1,B1,C1初值 时间间隔H, 计算精度EPs 计算:积分步长H0 调用变步长Runge--Kuta积分法子程序解动力学方程组计算时刻t 的A,B,[C值 (其中调用计算动力学方程组的子程序计算DY值) 列表输出:10min内每隔0.5min所对应的[A,B,C值 结束
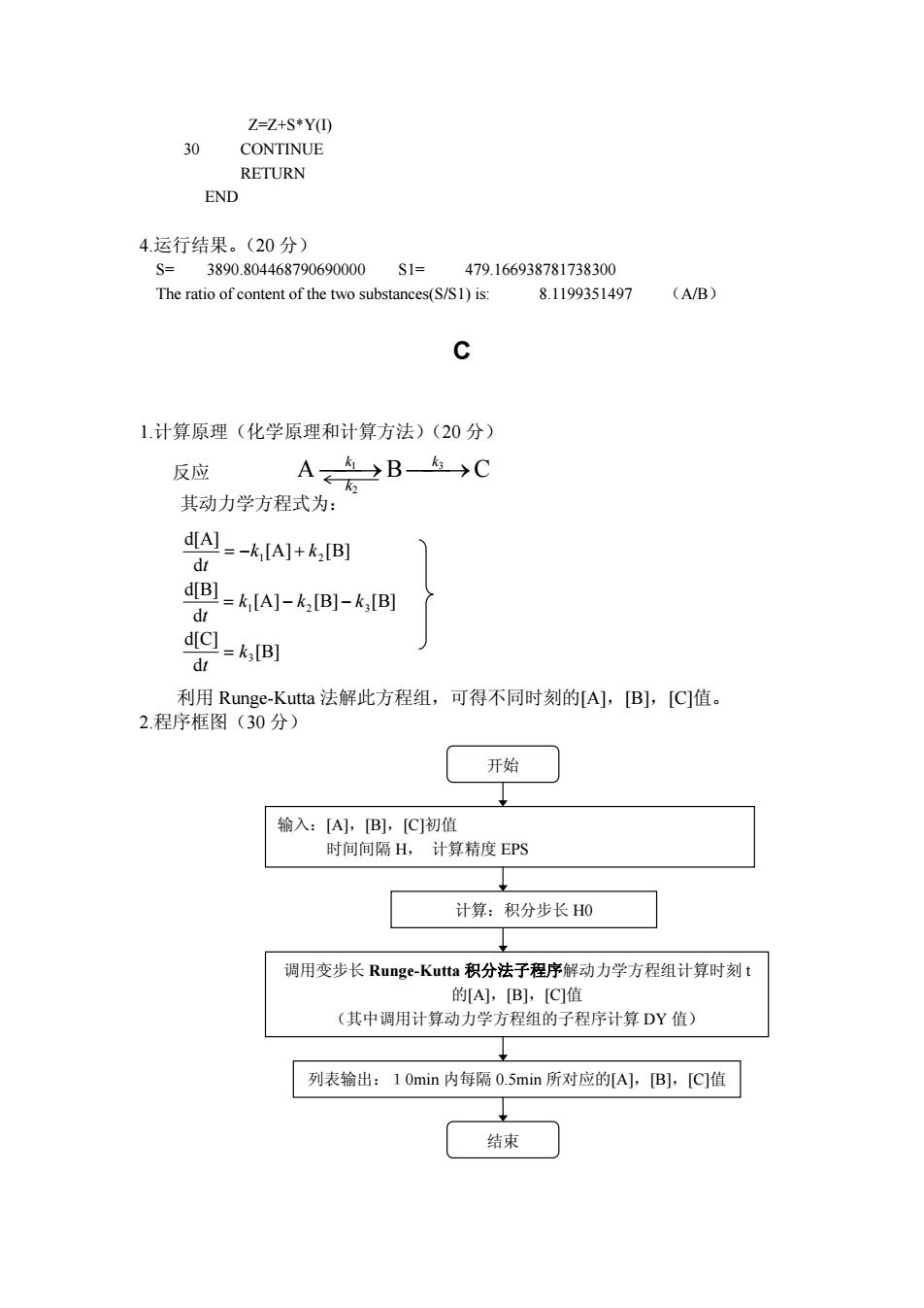
Z=Z+S*Y(I) 30 CONTINUE RETURN END 4.运行结果。(20 分) S= 3890.804468790690000 S1= 479.166938781738300 The ratio of content of the two substances(S/S1) is: 8.1199351497 (A/B) C 1.计算原理(化学原理和计算方法)(20 分) 反应 A ⎯⎯→1 B ⎯⎯→3 C k k 其动力学方程式为: [B] d d[C] [A] [B] [B] d d[B] [A] [B] d d[A] 3 1 2 3 1 2 k t k k k t k k t = = − − = − + 利用 Runge-Kutta 法解此方程组,可得不同时刻的[A],[B],[C]值。 2.程序框图(30 分) 开始 输入:[A],[B],[C]初值 时间间隔 H, 计算精度 EPS 计算:积分步长 H0 调用变步长 Runge-Kutta 积分法子程序解动力学方程组计算时刻 t 的[A],[B],[C]值 (其中调用计算动力学方程组的子程序计算 DY 值) 列表输出:10min 内每隔 0.5min 所对应的[A],[B],[C]值 结束 k2

3.源程序(30分) PROGRAM MAIN IMPLICIT REAL*8(A-H.O-Z DIMENSION YO(20),Y1(20),Y2(20) OPEN(6,FILE-TESTC.DAT,STATUS-'UNKNOWN) DATA Y0/0.01,0.0,0.0,17*0.0/ N-3 T0-0.0 T1=10.0 H0-0.5 EPS=1.0E-6 H=HO WRITE(6.11)N.TO,T1,H0.EPS WRITE(6.22)T0.H.(Y0(D.I-1.N M=IDINT((TI-TOVHO+0.5) D08010=1,M K=1 CALLRK4(TO.Y0.Y1.HO.N.K) D030KK=1,100 K-K+K H=HO/K CALLRK4(TO,Y0.Y2.H.N.K) ES=0.0 D010J=,N 10 ES-ES+ABS(Y2U)-Y10VY2U) IF(ES.LT.EPS)GOTO 50 D020J=1N YI(EY2() CONTINUE WRITE(6.3 3 STOP 50 T0=T0+H0 D060J=1,N 60 YOCY20) WRITE(6.22)T0.H.(Y2(T).I-1.N) 80 CONTINUE WRITE(6.44) 11 FORMATO/1XN=,2,2X,T0=,F6.1,2XT1=,F8.1,2X,& H0=.G8.3,1X,EPS=,G10.3/20X,Y①.=1,2,3.4N& 1X.66(1H-)/5X.'Umin'.3X.'H/min'.6X.'[A]/molL-I', 6X.[BlmolL-T'.6X.(CVmolL-T/1X.66(1H-) 22 F0RMAT(1X,2F8.2,2X,3G15.6) 33 FORMAT(/IX,'FAILED TO FIND STABLE SOLUTION IN MAX IT/) 44 FORMAT(IX.66(1H-))
3.源程序(30 分) PROGRAM MAIN IMPLICIT REAL *8(A-H,O-Z) DIMENSION Y0(20),Y1(20),Y2(20) OPEN(6,FILE='TESTC.DAT',STATUS='UNKNOWN') DATA Y0/0.01,0.0,0.0,17*0.0/ N=3 T0=0.0 T1=10.0 H0=0.5 EPS=1.0E-6 H=H0 WRITE(6,11)N,T0,T1,H0,EPS WRITE(6,22)T0,H,(Y0(I),I=1,N) M=IDINT((T1-T0)/H0+0.5) DO 80 I0=1,M K=1 CALL RK4(T0,Y0,Y1,H0,N,K) DO 30 KK=1,100 K=K+K H=H0/K CALL RK4(T0,Y0,Y2,H,N,K) ES=0.0 DO 10 J=1,N 10 ES=ES+ABS((Y2(J)-Y1(J))/Y2(J)) IF(ES.LT.EPS)GOTO 50 DO 20 J=1,N 20 Y1(J)=Y2(J) 30 CONTINUE WRITE(6,33) STOP 50 T0=T0+H0 DO 60 J=1,N 60 Y0(J)=Y2(J) WRITE(6,22)T0,H,(Y2(I),I=1,N) 80 CONTINUE WRITE(6,44) 11 FORMAT(/1X,'N=',I2,2X,'T0=',F6.1,2X,'T1=',F8.1,2X, & 'H0=',G8.3,1X,'EPS=',G10.3//20X,'Y(I),I=1,2,3,4,...,N' & 1X,66(1H-)/5X,'t/min',3X,'H/min',6X,'[A]/molL-1', & 6X,'[B]/molL-1',6X,'[C]/molL-1' /1X,66(1H-)) 22 FORMAT(1X,2F8.2,2X,3G15.6) 33 FORMAT(/1X,'FAILED TO FIND STABLE SOLUTION IN MAX IT'/) 44 FORMAT(1X,66(1H-))

END IMPLICIT RE REAL #8 K1.K2.K3 DIMENSION Y(20).,DY(20) DATA K1/0.0044/.K2/2.96/.K3/0.0021 K2*Y2-K3 Y(2) DY(3)=K2*Y(2 RETURN END SUBROUTINERK4(X0.Y0,Y.H.N.M) IMPLICIT REAL*8(A-H.O-Z) DIMENSION YO(N)Y(N) DIMENSION Y2(20).DY(20),RK(20) X=XO DO5I=1.N 5 Y(I)-YO(I) D050L=1,M CALL FCYDYY D010I=1N RK(I)-DY(I 10 Y20-Y00.5*H*DY CALL F(Y2,DY) D020I=1N RKOERKUH2DYOD Y20DEY(DH0 5*H*DYO) CALLF(Y2.DY) DO30I-I.N RK(I)=RK(I)+2◆DY(I 30 Y2I=Y④+HDYO CALL FCY2.DY) DO401=1N RK(D-RK(I)+DY( Y(IFY(I+RK(I)H/ 50 CONTINUE RETURN END END
END SUBROUTINE F(Y,DY) IMPLICIT REAL *8(A-H,O-Z) REAL *8 K1,K2,K3 DIMENSION Y(20),DY(20) DATA K1/0.0044/,K2/2.96/,K3/0.0021/ DY(1)=-K1*Y(1)+K3*Y(2) DY(2)=K1*Y(1)-K2*Y(2)-K3*Y(2) DY(3)=K2*Y(2) RETURN END SUBROUTINE RK4(X0,Y0,Y,H,N,M) IMPLICIT REAL *8(A-H,O-Z) DIMENSION Y0(N),Y(N) DIMENSION Y2(20),DY(20),RK(20) X=X0 DO 5 I=1,N 5 Y(I)=Y0(I) DO 50 L=1,M CALL F(Y,DY) DO 10 I=1,N RK(I)=DY(I) 10 Y2(I)=Y(I)+0.5*H*DY(I) CALL F(Y2,DY) DO 20 I=1,N RK(I)=RK(I)+2*DY(I) 20 Y2(I)=Y(I)+0.5*H*DY(I) CALL F(Y2,DY) DO 30 I=1,N RK(I)=RK(I)+2*DY(I) 30 Y2(I)=Y(I)+H*DY(I) CALL F(Y2,DY) DO 40 I=1,N RK(I)=RK(I)+DY(I) 40 Y(I)=Y(I)+RK(I)*H/6 50 CONTINUE RETURN END END