
北京化工大学2008一一2009学年第一学期 《计算化学》期末考试试卷标准答案 第一部分笔试部分(共30分) 一、判断题,正确的在括号中划“√”,错误的划“×”(每题1.5分,共15分) 1.V2.√3.×4.×5.x6.×7./8.×9.10.x 二、填空题(9-10题每空0.5分,其余每空一分,共15分) 1.将化学问题转变为数学模型。 2.差商。 3.分段插值法。 4.相关系数;1。 5.函数类型(或曲线类型)。 6.插值法。 7.一系列离散点:y=F(x),F(x)为原函数:化学动力学 8.不用求导,甚至在没有目标函数表达式的情况下也可使用;反射、收缩、 扩张。 9.分子绘图;数据处理:量子化学计算;分子模拟。 10.统计法调优、模拟法调优。 第二部分上机题(共70分) A 1.计算原理(化学原理和计算方法)(15分) 设反应达平衡时SO3的物质的量为xmol,有 2S02(g)+02(g)=2S03(g)
1 北京化工大学 2008——2009 学年第一学期 《计算化学》期末考试试卷标准答案 第一部分 笔试部分(共 30 分) 一、判断题,正确的在括号中划“3”,错误的划“2”(每题 1.5 分,共 15 分) 1. 3 2. 3 3. 2 4. 2 5. 2 6. 2 7. 3 8. 2 9. 3 10. 2 二、填空题(9-10 题每空 0.5 分,其余每空一分,共 15 分) 1.将化学问题转变为数学模型。 2.差商。 3.分段插值法。 4.相关系数;1。 5.函数类型(或曲线类型)。 6.插值法。 7.一系列离散点; y = F(x) , F(x)为原函数;化学动力学 8.不用求导,甚至在没有目标函数表达式的情况下也可使用;反射、收缩、 扩张。 9.分子绘图;数据处理;量子化学计算;分子模拟。 10.统计法调优、模拟法调优。 第二部分 上机题(共 70 分) A 1.计算原理(化学原理和计算方法)(15 分) 设反应达平衡时 SO3 的物质的量为 x mol,有 2SO2(g)+O2(g) 2SO3(g)

起始物质的量mol 1 1 0 平衡物质的量/mol 1-x 1-0.5x 反应达平衡时系统中总物质的量为:1-x+1-0.5x+x=2-0.5x 故平衡时系统中各物质的组成为: 1-x 1-0.5x ys0:=2-0.5x y0,=2-0.5x y90,=2-0.5x 式中:y为物质的量分数。 (4分) 代入平衡关系式得: x2「p 7 K"=2p-a-i-0a-5 (1) 由热力学原理知计算标准平衡常数的基本公式为 △,G=-RTIn K1 只要知道标准摩尔反应吉布斯自由能函数值△,G,即可求出标准平衡常数 Kcon) (2)(3分) 标准摩尔反应吉布斯自由能函数又可由己知的各组分的标准摩尔生成吉布 斯自由能函数△GB来计算: △,Ga(T)=∑yB△GaB(T) (3)(2分) (1)式经整理后得 x2 p (4) 1-x)21-0.5x)(2-0.5x)p° -K8=0 x2「p 令:f)=-xr0-05xL2-0.5xp -K8=0 (3分) 调用二分法求解方程(x)=0,即可求出反应达平衡时系统的组成和SO, 的转化率(=x)。 取值范围:0.0~1.0 (3分)
2 起始物质的量/mol 1 1 0 平衡物质的量/mol 1-x 1-0.5x x 反应达平衡时系统中总物质的量为: 1− x +1− 0.5x + x = 2 − 0.5x 故平衡时系统中各物质的组成为: , 2 0.5 2 0.5 1 0.5 , 2 0.5 1 3 2 2 SO SO O x x y x x y x x y − = − − = − − = 式中:y 为物质的量分数。 (4 分) 代入平衡关系式得: 1 2 2 (1 ) (1 0.5 ) (2 0.5 ) ( ) B − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − − − = ∑ = ∑ θ B n x p p x x x n p p K K ν θ θ (1) 由热力学原理知计算标准平衡常数的基本公式为 θ θ ΔrGm = −RT ln K 只要知道标准摩尔反应吉布斯自由能函数值 θ ΔrGm ,即可求出标准平衡常数 exp( ) m RT G K r θ θ Δ = − (2)(3 分) 标准摩尔反应吉布斯自由能函数又可由已知的各组分的标准摩尔生成吉布 斯自由能函数 θ Δ f Gm,B 来计算: ( ) ( ) rGm T B B f Gm,B T θ θ Δ = ∑ ν Δ (3)(2 分) (1)式经整理后得 0 (1 ) (1 0.5 ) (2 0.5 ) 1 2 θ 2 − = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − − − − θ K x p p x x x (4) 令: 0 (1 ) (1 0.5 ) (2 0.5 ) ( ) 1 2 θ 2 − = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − − − = − θ K x p p x x x f x (3 分) 调用二分法求解方程 0 f (x) = ,即可求出反应达平衡时系统的组成和SO2 的转化率(=x)。 取值范围 :0.0~1.0 (3 分)
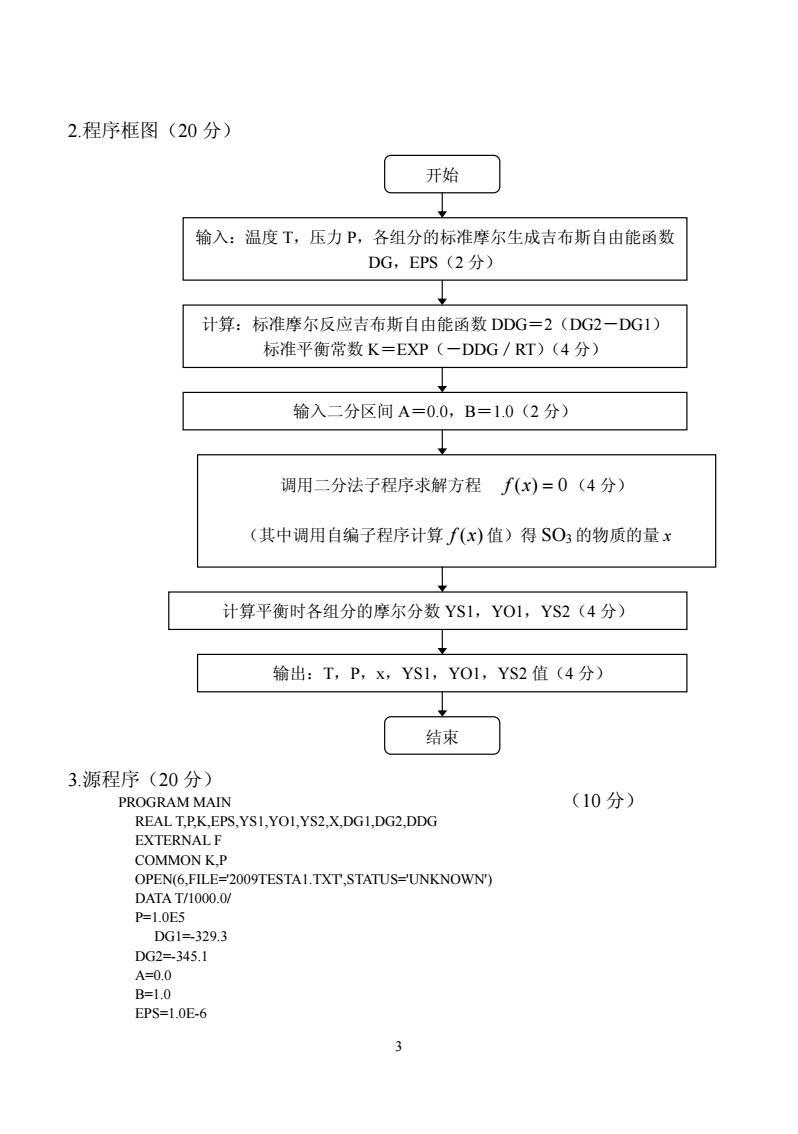
2.程序框图(20分) 开始 输入:温度T,压力P,各组分的标准摩尔生成吉布斯自由能函数 DG,EPS(2分) 计算:标准摩尔反应吉布斯自由能函数DDG=2(DG2-DG1 标准平衡常数K=EXP(一DDG/RT)(4分) 输入二分区间A=0.0,B=1.0(2分)》 调用二分法子程序求解方程f(x)=0(4分) (其中调用自编子程序计算f(x)值)得SO3的物质的量x 计算平衡时各组分的摩尔分数YS1,YO1,YS2(4分) 输出:T,P,x,YS1,YO1,YS2值(4分) 结束 3.源程序(20分) PROGRAM MAIN (10分) REALT.P.K,EPS.YSI,YO1,YS2,X,DGI.DG2,DDG EXTERNALF COMMON K,P OPEN(6,FILE-2009TESTAI.TXT,STATUS-UNKNOWN) DATA T/1000.0/ P=1.0E5 DG1=329.3 DG2=345.1 A=0.0 B=1.0 EPS=1.0E-6
3 2.程序框图(20 分) 3.源程序(20 分) PROGRAM MAIN (10 分) REAL T,P,K,EPS,YS1,YO1,YS2,X,DG1,DG2,DDG EXTERNAL F COMMON K,P OPEN(6,FILE='2009TESTA1.TXT',STATUS='UNKNOWN') DATA T/1000.0/ P=1.0E5 DG1=-329.3 DG2=-345.1 A=0.0 B=1.0 EPS=1.0E-6 开始 计算:标准摩尔反应吉布斯自由能函数 DDG=2(DG2-DG1) 标准平衡常数 K=EXP(-DDG/RT)(4 分) 调用二分法子程序求解方程 f (x) = 0(4 分) (其中调用自编子程序计算 f (x) 值)得 SO3 的物质的量 x 输出:T,P,x,YS1,YO1,YS2 值(4 分) 结束 输入二分区间 A=0.0,B=1.0(2 分) 计算平衡时各组分的摩尔分数 YS1,YO1,YS2(4 分) 输入:温度 T,压力 P,各组分的标准摩尔生成吉布斯自由能函数 DG,EPS(2 分)

R=8.314 (A.B.E PS.F.X) YSI=U-XM Yo1=1-0.5X2-0.5X 11 5X.X-.F6.4//RESULT/5X O2=F6.4& 5X3O2F645XSO3F64 END FUNCTION FX) (5分) DEAI YDK COMMON K.P F=X*X/1-X*21-0.5*X)(2-0.5*X*1.0E5/PyK RETURN END SUBROUTINE HALF(A,B,EPS,F,X) (5分) REALA.B.EPS YO=F(A) A1三A BI=B K=0 10 X气A1+B1)*0.5 Y=F(X) IF(Y*Y0.GT.0.0)AI=X IECY+YOLEOORI=X IF(ABS(BI-AIVX.GTEPSIGOTO 10 K=K+1 IF(K GT.50)THEN WRITE◆,YNO RESOLUTION G0T030 END IF X=A1+B1)*0.5 30 RETURN END 4.运行结果(15分) T=1000.0000K .1000E+06Pa X=.4004 (5分) RESULT: y(S02-.3331 (5分) y(02F.4444 (5分) y(S03F2225 (5分) ¥
4 R=8.314 DDG=2*(DG2-DG1) K=EXP(-(DDG/R/T)) CALL HALF(A,B,EPS,F,X) YS1=(1-X)/(2-0.5*X) YO1=(1-0.5*X)/(2-0.5*X) YS2=X/(2-0.5*X) WRITE(6,11)T,P,X,YS1,YO1,YS2 11 FORMAT(/5X,'T=',F10.4,'K'/5X,'P=',G12.4,'Pa'/& /5X,'X=',F6.4//'RESULT:'/5X,'y(SO2)=',F6.4 & /5X,'y(O2)=',F6.4 /5X,'y(SO3)=',F6.4 ) END FUNCTION F(X) (5 分) REAL X,P,K COMMON K,P F=((X*X)/((1-X)**2)/(1-0.5*X))*((2-0.5*X)*1.0E5/P)-K RETURN END SUBROUTINE HALF(A,B,EPS,F,X) (5 分) REAL A,B,EPS Y0=F(A) A1=A B1=B K=0 10 X=(A1+B1)*0.5 Y=F(X) IF(Y*Y0.GT.0.0)A1=X IF(Y*Y0.LE.0.0)B1=X IF(ABS(B1-A1)/X.GT.EPS)GOTO 10 K=K+1 IF(K.GT.50) THEN WRITE(*,*)'NO RESOLUTION' GOTO 30 END IF X=(A1+B1)*0.5 30 RETURN END 4.运行结果(15 分) T= 1000.0000K P= .1000E+06Pa X= .4004 (5 分) RESULT: y(SO2)= .3331 (5 分) y(O2)= .4444 (5 分) y(SO3)= .2225 (5 分)

B 1.计算原理(化学原理和计算方法)(15分)》 根据反应式 乙苯(EB)零级,4→氢化过氧化物(H)二级,→醇酮等副产物(MA) 可以写出氢化过氧化物(H)的速率方程 dc且=k-k,c日 (1) c是氢化过氧化物的浓度,式(1)可写为 dcu =(k -kzci)dt (5分) 考虑到初始条件下=0时,©阳=0,则在对应区间上积分得 Cn =f"den =kifdt-k2 fcid Cu =kt-k2 cidt (2) (3分) (2)式两端同时除以1(0时.并令y=9,X-c 一,则式(2)可 写为 Y=k-k2X (3)(3分) 利用最小二乘法对(3)式进行一元线性回归,可得到第一步和第二步的反 应速率常数k、2。 在此前,要根据测定的c如数据组来计算次生数据[cd, cid=cid+∫,cid ”cd可直接用梯形法求,,cd可采用数值积分中离散点求积的方法(用 Simpson求积方法,其中调用Lagrange插值法子程序计算任意点的函数值)。 (4分) 2.程序框图(20分) 开始
5 B 1. 计算原理(化学原理和计算方法)(15 分) 根据反应式 乙苯(EB)⎯零级, ⎯ → ⎯⎯k1 氢化过氧化物(H)⎯二级, ⎯ → ⎯⎯k2 醇酮等副产物(MA) 可以写出氢化过氧化物(H)的速率方程 2 1 2 H H d d k k c t c = − (1) cH是氢化过氧化物的浓度,式(1)可写为 dc (k k c )dt 2 H = 1 − 2 H (5 分) 考虑到初始条件下 t=0 时,cH=0,则在对应区间上积分得 ∫ ∫ ∫ = = − c t t c c k t k c t 0 2 2 H 0 1 0 H H d d d H ∫ = − t c k t k c t 0 2 H 1 2 H d (2) (3 分) (2)式两端同时除以 t(t>0 时),并令 t c t X t c Y t ∫ = = 0 2 H H d , ,则式(2)可 写为 Y = k1 − k2 X (3) (3 分) 利用最小二乘法对(3)式进行一元线性回归,可得到第一步和第二步的反 应速率常数 k1、k2。 在此前,要根据测定的 t~cH数据组来计算次生数据 ∫ t c t 0 2 Hd , ∫ t c t 0 2 Hd =∫ ∫ + t c t c t 4.7 2 H 4.7 0 2 Hd d ∫ 4.7 0 2 Hc dt 可直接用梯形法求,∫ t c t 4.7 2 Hd 可采用数值积分中离散点求积的方法(用 Simpson 求积方法,其中调用 Lagrange 插值法子程序计算任意点的函数值)。 (4 分) 2. 程序框图(20 分) 开始
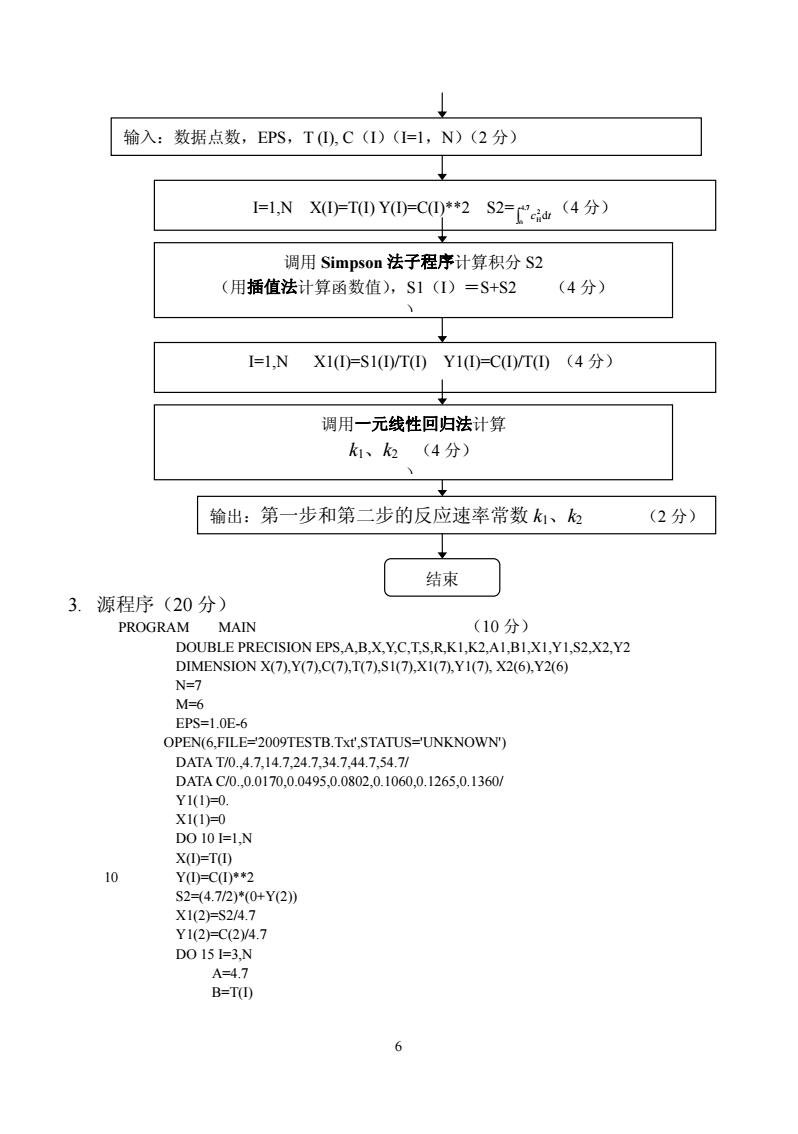
输入:数据点数,EPS,T①,C(I)(=1,N)(2分) 曰,NX0T0Y0-C02S2=(4分) 调用Simpson法子程序计算积分S2 (用插值法计算函数值),S1(I)=S+S2(4分) I=1,NX1①F=S1①/T①Y1①=C①/T④(4分) 调用一元线性回归法计算 k1、k2(4分) 输出:第一步和第二步的反应速率常数k、 (2分) 结束 3.源程序(20分) PROGRAM MAIN (10分) DOUBLEPRECISIONEPS.A.B.X.Y.C.T.S.R.K1.K2.A1.B1.X1.Y1.S2.X2.Y2 DIMENSION X(7.Y(7).C(7)T(7).SI(7.XI(7).YI(7).X2(6).Y2(6) -7 M-6 EPS-1 0E6 OPEN(6.FILE-2009TESTB.Txt',STATUS-'UNKNOWN) DATA TA0.4.7.14.7.24.7.34.7.447.54.71 DATA CA0.0.0170.0.0495.008020.1060.0.1265,0.1360/ Y11=0. X1(1=0 D010=l,N XOETO 10 Y①-CU*2 S24.72)*(0+Y2) X1(2=S24.7 Y1(2=C2y4.7 D015I=3.N A=47 B=T④ 6
6 3. 源程序(20 分) PROGRAM MAIN (10 分) DOUBLE PRECISION EPS,A,B,X,Y,C,T,S,R,K1,K2,A1,B1,X1,Y1,S2,X2,Y2 DIMENSION X(7),Y(7),C(7),T(7),S1(7),X1(7),Y1(7), X2(6),Y2(6) N=7 M=6 EPS=1.0E-6 OPEN(6,FILE='2009TESTB.Txt',STATUS='UNKNOWN') DATA T/0.,4.7,14.7,24.7,34.7,44.7,54.7/ DATA C/0.,0.0170,0.0495,0.0802,0.1060,0.1265,0.1360/ Y1(1)=0. X1(1)=0 DO 10 I=1,N X(I)=T(I) 10 Y(I)=C(I)**2 S2=(4.7/2)*(0+Y(2)) X1(2)=S2/4.7 Y1(2)=C(2)/4.7 DO 15 I=3,N A=4.7 B=T(I) 输入:数据点数,EPS,T (I), C(I)(I=1,N)(2 分) I=1,N X(I)=T(I) Y(I)=C(I)**2 S2=∫ 4.7 0 2 cHdt (4 分) 调用 Simpson 法子程序计算积分 S2 (用插值法计算函数值),S1(I)=S+S2 (4 分) ) 输出:第一步和第二步的反应速率常数 k1、k2 (2 分) 结束 I=1,N X1(I)=S1(I)/T(I) Y1(I)=C(I)/T(I) (4 分) 调用一元线性回归法计算 k1、k2 (4 分) )

CALLSIMP(N,A,B.X,Y,EPS,S) S1①=S+S2 X1①=S1①/TD 15 Y10=CO/T④ D016=1,M X2(I)=XI(l+1) Y2①=Y1+1) 16 CONTINUE CALL PK(M,X2,Y2,AI,BI,R) KI=AI K2=B1 WRITE(6,20)K1,K2,R 20 FORMAT(5X.'KI=,G12.6,2X.'mol-dm-3-min-1'/& 5X.K2=.G12.62X'mol-1dm3-min-1"/5X.R=G12.6 END SUBROUTINE SIMP(M.A.B.X.Y.EPS.S2) (4分) DOUBLE PRECISION A.B.X.Y.EPS.S2.FA.FB.XO.YO DIMENSION X(M)Y(M) H=B-A N=1 CALL LGRG2(X.Y.M.A.FAY CALL LGRG2(X.Y.M.B.FB) T1=0.5*H(FA+FB) 10 S=U D020K=1,N X0=A+HK-0.5)* CALL LGRG2(X,YM XO,YO) 20 =+Y0 T2=0.5*T1+H*S 5. IF(N.EQ.I)GOTO 40 D=ABS(S2-ST) IF(ABS(S2).GT.1.0)THEN BS((S2-S1yS2) IF(D LT.EPS)GOTO 50 40 50 RET END (3分) UBLE PRECISION X.Y.TZ.S
7 CALL SIMP(N,A,B,X,Y,EPS,S) S1(I)=S+S2 X1(I)=S1(I)/T(I) 15 Y1(I)=C(I)/T(I) DO 16 I=1,M X2(I)=X1(I+1) Y2(I)=Y1(I+1) 16 CONTINUE CALL PK(M,X2,Y2,A1,B1,R) K1=A1 K2=-B1 WRITE(6,20) K1,K2,R 20 FORMAT(5X,'K1=',G12.6,2X,'mol·dm-3·min-1',/& 5X,'K2=',G12.6,2X,'mol-1·dm3·min-1',/5X,'R=',G12.6) END SUBROUTINE SIMP(M,A,B,X,Y,EPS,S2) (4 分) DOUBLE PRECISION A,B,X,Y,EPS,S2,FA,FB,X0,Y0 DIMENSION X(M),Y(M) H=B-A N=1 CALL LGRG2(X,Y,M,A,FA) CALL LGRG2(X,Y,M,B,FB) T1=0.5*H*(FA+FB) 10 S=0 DO 20 K=1,N X0=A+(K-0.5)*H CALL LGRG2(X,Y,M,X0,Y0) 20 S=S+Y0 T2=0.5*(T1+H*S) S2=T2+(T2-T1)/3.0 IF(N.EQ.1)GOTO 40 30 D=ABS(S2-S1) IF(ABS(S2).GT.1.0)THEN D=ABS((S2-S1)/S2) END IF IF(D.LT.EPS)GOTO 50 40 N=N+N H=0.5*H T1=T2 S1=S2 GOTO 10 50 RETURN END SUBROUTINE LGRG2(X,Y,N,T,Z) (3 分) DIMENSION X(N),Y(N) DOUBLE PRECISION X,Y,T,Z,S Z=0.0 IF(N.LE.0)RETURN

IF(N.EQ.I)THEN RE END IE JRN (2Y(2)T-X1))MX(1)X(2》 END IF L.LE.X(2))THEN M= ELSE IF(T.GE.X(N-1))THEN N M-N 且SE K-I M-N 10 IF(LABS(K-M).NE.I)THEN L=K+M①2 IF(T.LTX(L)THEN M=I EISE K=I ENDIF G0T010 ENDIE IF(ABS(T-X(K)).LT.ABS(T-X(M))THEN K=K,1 ELS M-M+1 END IF END IE 7=00 D030=K,M S=10 DO 20 J=K.M IF(J.NE.D)THEN S=S(T-X(V(X(D-X()) END IE 名 CONTINUE Z=Z+S*Y(I) CONTINUE Return END SUBROUTINE PK(N.X,Y.A,B.R) (3分) DOUBLE PRECISION XYABR DIMENSION X(N),Y(N) SX=0.0 sY=0.0
8 IF(N.EQ.1)THEN Z=Y(1) RETURN END IF IF(N.EQ.2)THEN Z=(Y(1)*(T-X(2))-Y(2)*(T-X(1)))/(X(1)-X(2)) RETURN END IF IF(T.LE.X(2))THEN K=1 M=3 ELSE IF(T.GE.X(N-1))THEN K=N-2 M=N ELSE K=1 M=N 10 IF(IABS(K-M).NE.1)THEN L=(K+M)/2 IF(T.LT.X(L))THEN M=L ELSE K=L ENDIF GOTO 10 END IF IF(ABS(T-X(K)).LT.ABS(T-X(M))) THEN K=K-1 ELSE M=M+1 END IF END IF Z=0.0 DO 30 I=K,M S=1.0 DO 20 J=K,M IF(J.NE.I)THEN S=S*(T-X(J))/(X(I)-X(J)) END IF 20 CONTINUE Z=Z+S*Y(I) 30 CONTINUE RETURN END SUBROUTINE PK(N,X,Y,A,B,R) (3 分) DOUBLE PRECISION X,Y,A,B,R DIMENSION X(N),Y(N) SX=0.0 SY=0.0

SXX=0.0 SYY-0.0 SXY=0.0 D010=1,N X1=X0) YIY() SX=SX+XI SY=SY+YI SXX=SXX+X1*XI SYY=SYY+YIY SXY-SXY+X1*YI 10 CONTINUE DXX=SXX-SXSX/N DYY=SYY-SY*SY/N DXY=SXY-SX*SY/N B-DXY/DXX A=(SY-BSXVN R=DXY/SQRT(DXX*DYY) RETURN END 4.运行结果(15分) K1=355828E-02 moldm-3-min-I (5分) K2=.124650 mol-1dm3-min-1 (5分) R=-988781 (5分) Q 1.计算原理(化学原理和计算方法)(15分) 某厂以萘为原料在列管式固定床反应器中生产苯酐。己知萘的转化率和温 度沿床层的变化率分别为 11094x10'(1o0-05x 1-x 1409 dz m dr=76120×10( 1-x d 0-0rk学 9.9282(T-T)K·m 式中:一萘的转化率:2一反应管长,m:T一反应温度,K: Tw一反应管壁温度,K。 假定反应器入口温度为613K,萘转化率x0=0,反应管内壁温度靠管外熔 盐加热,温度稳定在613K,设反应管长为10m, 9
9 SXX=0.0 SYY=0.0 SXY=0.0 DO 10 I=1,N X1=X(I) Y1=Y(I) SX=SX+X1 SY=SY+Y1 SXX=SXX+X1*X1 SYY=SYY+Y1*Y1 SXY=SXY+X1*Y1 10 CONTINUE DXX=SXX-SX*SX/N DYY=SYY-SY*SY/N DXY=SXY-SX*SY/N B=DXY/DXX A=(SY-B*SX)/N R=DXY/SQRT(DXX*DYY) RETURN END 4. 运行结果(15 分) K1= .355828E-02 mol·dm-3·min-1 (5 分) K2= .124650 mol-1·dm3·min-1 (5 分) R=-.988781 (5 分) C 1.计算原理(化学原理和计算方法)(15 分) 某厂以萘为原料在列管式固定床反应器中生产苯酐。已知萘的转化率和温 度沿床层的变化率分别为 1 w 14098 12 1 14098 11 )e 9.9282( ) K m 1000 0.5 1 7.6120 10 ( d d )e m 1000 0.5 1 1.1094 10 ( d d − − − − − − ⋅ − − = × − − = × T T x x z T x x z x T T 式中:x——萘的转化率;z——反应管长,m;T——反应温度,K; TW——反应管壁温度,K。 假定反应器入口温度为 613K,萘转化率 x0=0,反应管内壁温度靠管外熔 盐加热,温度稳定在 613K,设反应管长为 10 m

欲计算反应器内每隔1.0m转化率及温度分布,需建立微分方程组进行求 解,这是一个常微分方程组的初值问题: =1.1094×10" 1- 1409% -)e d 1000-0.5 m dr=76120x109(100-05x 1-x 1409 -9.9282(T-T)Km 20-0m,x0=0,T。=613K (10分) 调用Runge-Kutta法解上述常微分方程组,可得到反应器内每隔1.0m转化 率及温度分布。 (5分) 2.程序框图(20分) 开始 输入:x;,T初值,TwT0 管长间隔,计算精度EPS (5分 计算:积分步长H(5分) 调用Runge-Kuta法子程序解方程组计算反应器内每隔1.0m转 化率及温度变化。 (5分) (自编子程序计算F(但) 列表输出:L,XT(5分) 结束 3源程序(20分) PROGRAM MAIN (10分) IMPLICIT REAL8(A-H.O-Z) DIMENSION YO(10).Y1(10).Y2(10)
10 欲计算反应器内每隔 1.0 m 转化率及温度分布,需建立微分方程组进行求 解,这是一个常微分方程组的初值问题: 1 w 14098 12 1 14098 11 )e 9.9282( ) K m 1000 0.5 1 7.6120 10 ( d d )e m 1000 0.5 1 1.1094 10 ( d d − − − − − − ⋅ − − = × − − = × T T x x z T x x z x T T z0=0 m, x0=0, K T0 = 613 (10 分) 调用 Runge-Kutta 法解上述常微分方程组,可得到反应器内每隔 1.0 m 转化 率及温度分布。 (5 分) 2.程序框图(20 分) 3.源程序(20 分) PROGRAM MAIN (10 分) IMPLICIT REAL *8(A-H,O-Z) DIMENSION Y0(10),Y1(10),Y2(10) 开始 输入:x;z,T 初值,Tw, T0 管长间隔, 计算精度 EPS (5 分) 计算:积分步长 H(5 分) 调用 Runge-Kutta 法子程序解方程组计算反应器内每隔 1.0 m转 化率及温度变化。 (5 分) (自编子程序计算 F (z)) 列表输出:L,x, T (5 分) 结束