第二章 实验数据的拟合及模型参数的确定 J合D 1.什么是实验数据的拟合及模型参数的确定? 从实验数据确定函数关系式=f), 以预测任意x值时的函数y值 例:298K时,SbH,(g)在Sb(s)上的分解的数据如下: tis 0 5 10 15 20 25 PSbH3 101.33 74.07 51.57 33.13 14.15 9.24 /Kpa aA→产物 r4:化学反应速率 09 PA:SbH的分压 k。:反应表观速率常数 :反应级数
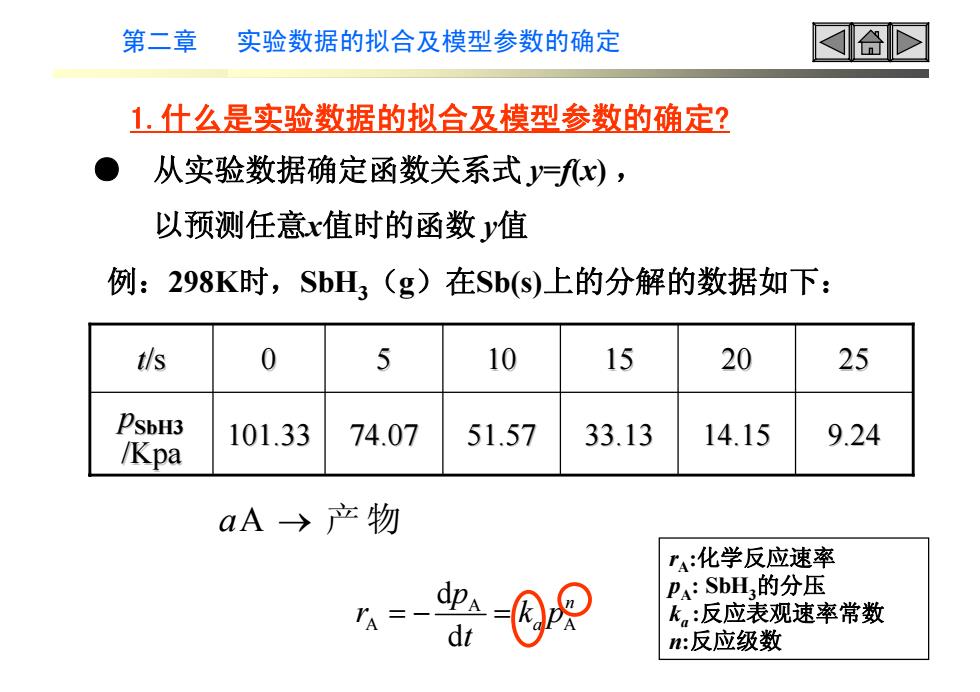
第二章 实验数据的拟合及模型参数的确定 1.什么是实验数据的拟合及模型参数的确定? ● 从实验数据确定函数关系式 y =f(x ) , 以预测任意x值时的函数 y 值 例:298K时,SbH 3 ( g)在Sb(s)上的分解的数据如下: 101.33 74.07 51.57 33.13 14.15 9.24 pSbH3 /Kpa t/s 0 5 10 15 20 25 a A → 产 物 A A A d d n a p r kp t =− = rA:化学反应速率 p A: SbH 3的分压 ka :反应表观速率常数 n:反应级数
数学模型中各参数的确定 合少 利用实验得到的全部信息,确定数学模型中的待定参数 例:镍硅藻土上苯加氢合成环己烷是表面反应控制的固体 催化剂上的气相反应。在160C,微分反应器中的初始 反应速率方程为 实验测定 +b④ 可确定模型参数 ka 表观速率常数 bu H,的吸附系数 b— C6H,的吸附系数
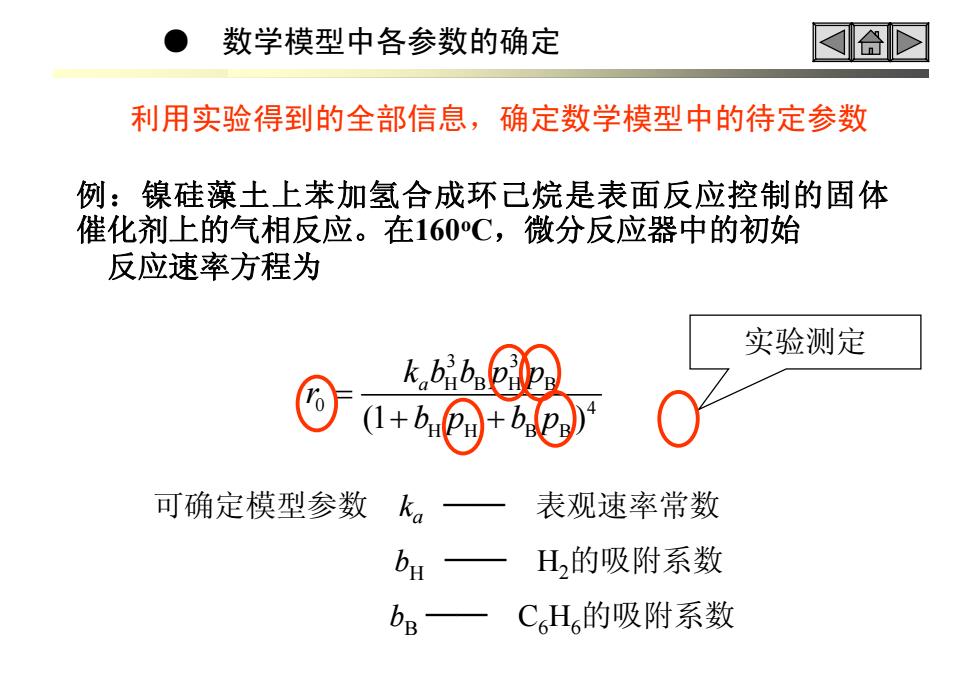
● 数学模型中各参数的确定 3 3 HB H B 0 4 HH BB (1 ) a kbb p p r bp bp = + + 例:镍硅藻土上苯加氢合成环己烷是表面反应控制的固体 催化剂上的气相反应。在160 o C,微分反应器中的初始 反应速率方程为 可确定模型参数 ka ── 表观速率常数 b H ── H 2的吸附系数 b B ── C 6 H 6的吸附系数 利用实验得到的全部信息,确定数学模型中的待定参数 实验测定
引言:2.常用的数学方法 插值法 函数关系 线性插值 ● Lagrangef插值 ●埃米尔特插值 回归分析 相关关系 ● 一元线性回归★ ● 线性模型的推广★ 多元回归*可化为多元线性回归的问题 多项式拟合简介 。逐次回归分析 数值微分 回
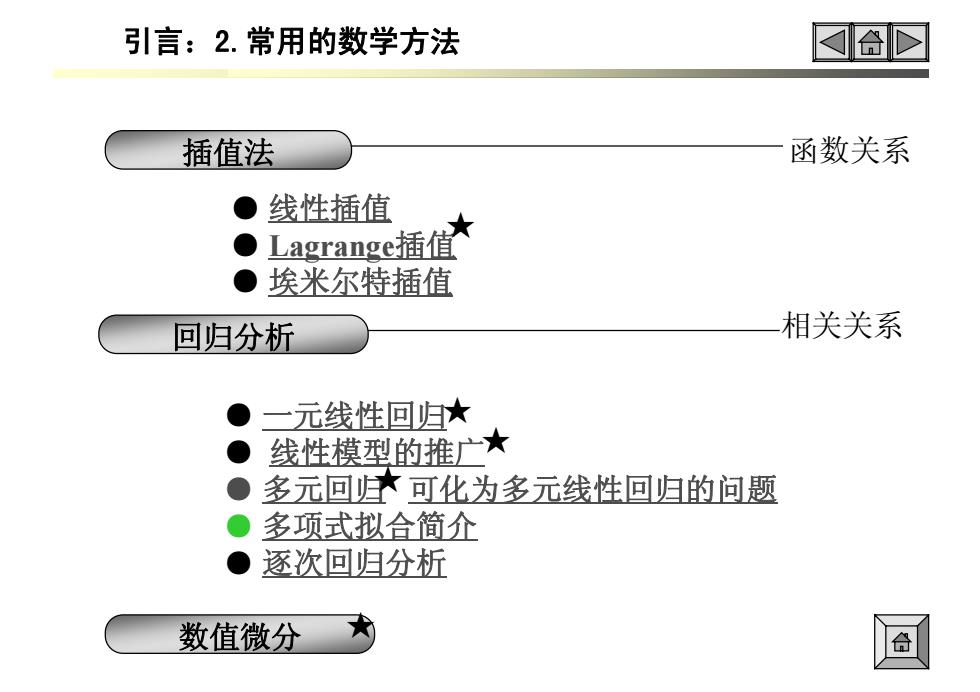
● 线性插值 ● Lagrange插值 ● 埃米尔特插值 ● 一元线性回归 ● 线性模型的推广 ● 多元回归 可化为多元线性回归的问题 ● 多项式拟合简介 ● 逐次回归分析 插值法 函数关系 回归分析 相关关系 数值微分 ★ ★ ★ ★ ★ 引言:2.常用的数学方法
2-1-1-1线性插值 问题的提出 合D 例:72型分光光度计测得某试样的吸收值如下: 入/nm 430 440 450 460 470 480 A 0.410 0.375 0.325 0.280 0.240 0.205 求在435,445,455,465,475nm处的吸收值。 希望:根据给定的函数表作一个既能反应x)的特性,又便 于计算的简单函数px),用px)近似fx),计算出任意 x对应的y值
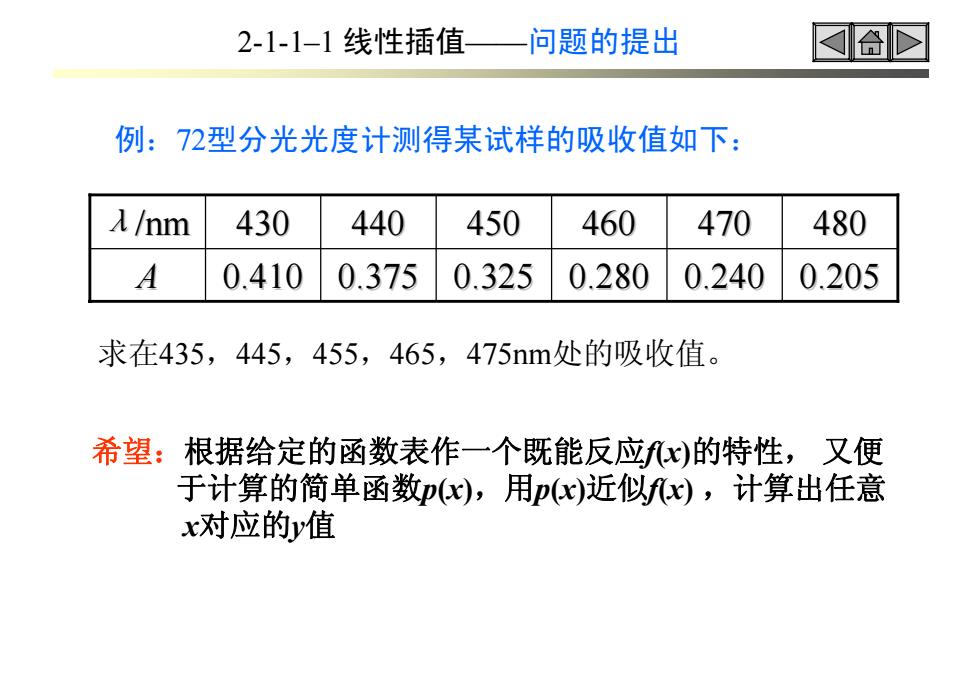
例:72型分光光度计测得某试样的吸收值如下: 2-1-1–1 线性插值——问题的提出 A 0.410 0.375 0.325 0.280 0.240 0.205 λ/nm 430 440 450 460 470 480 希望:根据给定的函数表作一个既能反应f(x)的特性, 又便 于计算的简单函数p(x),用p(x)近似f(x) ,计算出任意 x对应的y值 求在435,445,455,465,475nm处的吸收值
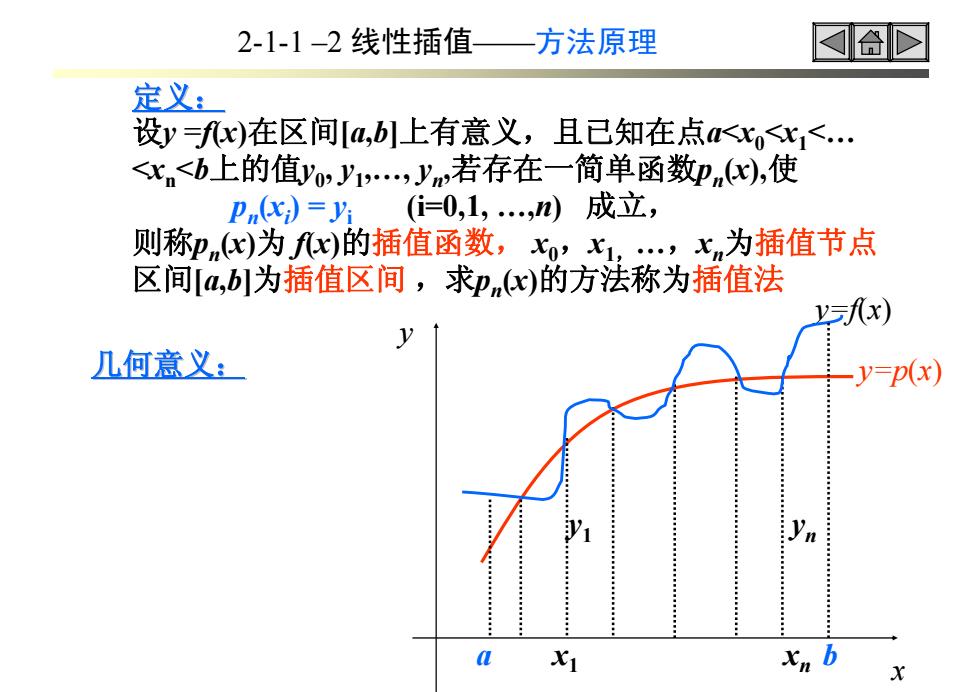
2-1-1-2线性插值 方法原理 定义: 设y=fx)在区间[a,b1上有意义,且己知在点<<x<… <x<b上的值,y1,yn若存在一简单函数即n,使 P)=片.(i=0,1,…m)成立, 则称pn)为fy)的插值函数,,X,,xn为插值节点 区间[a,b]为插值区间,求pnx)的方法称为插值法 vfx) 几何意义: -y=p(x) Xn
定义: 设y =f(x)在区间[a,b]上有意义,且已知在点a<x0<x1<… <xn<b上的值y0, y1,…, yn,若存在一简单函数pn(x),使 pn(xi) = yi (i=0,1, …,n) 成立, 则称pn(x)为 f(x)的插值函数, x0,x1,…,xn为插值节点 区间[a,b]为插值区间 ,求pn(x)的方法称为插值法 x y y=f(x) y=p(x) x1 y1 xn yn 几何意义: 2-1-1 –2 线性插值——方法原理 a b
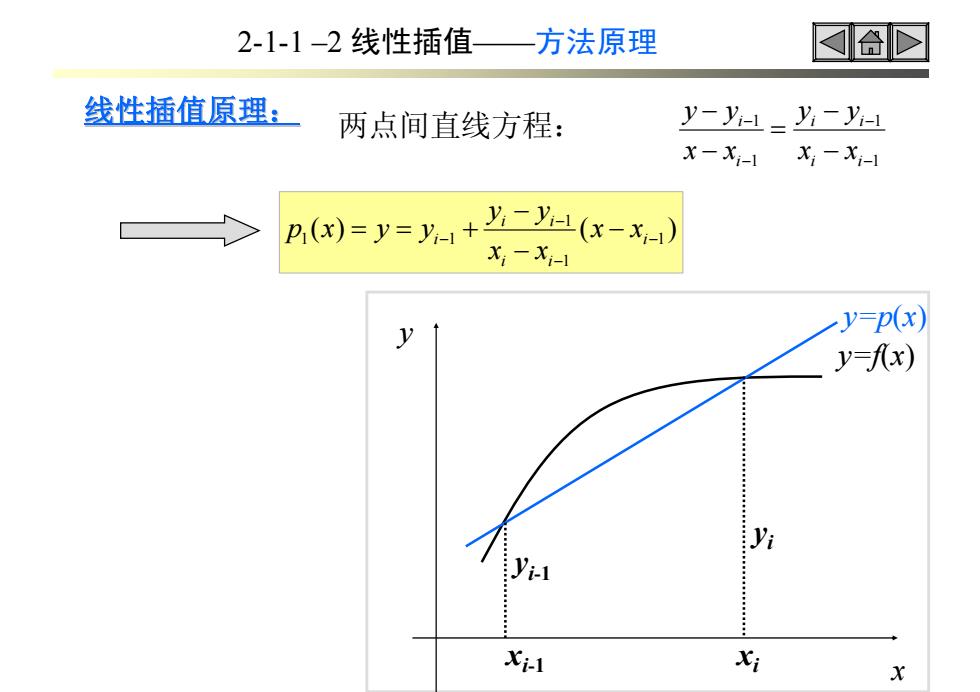
2-1-1-2线性插值— 方法原理 线性插值原理: 两点间直线方程: y-yi-1_yi-yi- X-X-1 Xi-Xi-1 p,()=y=y+Y-(x-x) X-Xi-1 y=p(x) y y=fx) Xi-1 Xi
线性插值原理: 线性插值原理: 两点间直线方程: 1 1 1 1 − − − − − − = − − i i i i i i x x y y x x y y ( ) ( )1 1 1 1 1 − − − − − − − = = + i i i i i i x x x x y y p x y y x y y=f(x) y=p(x) xi-1 yi-1 xi yi 2-1-1 –2 线性插值——方法原理

2-1-1-2线性插值 方法原理 分段线性插值: 实验点个数为n时,求插值结点x的 函数值。首先确定x在哪两点间 xXn-
分段线性插值: 分段线性插值: 实验点个数为n时,求插值结点 x的 函数值。首先确定x在哪两点间 xi < ≤ = − = ≤ − − − = + n i i J J J J J J n x x i x x x i n J x x y y x x x x y x y L 2-1-1 –2 线性插值——方法原理
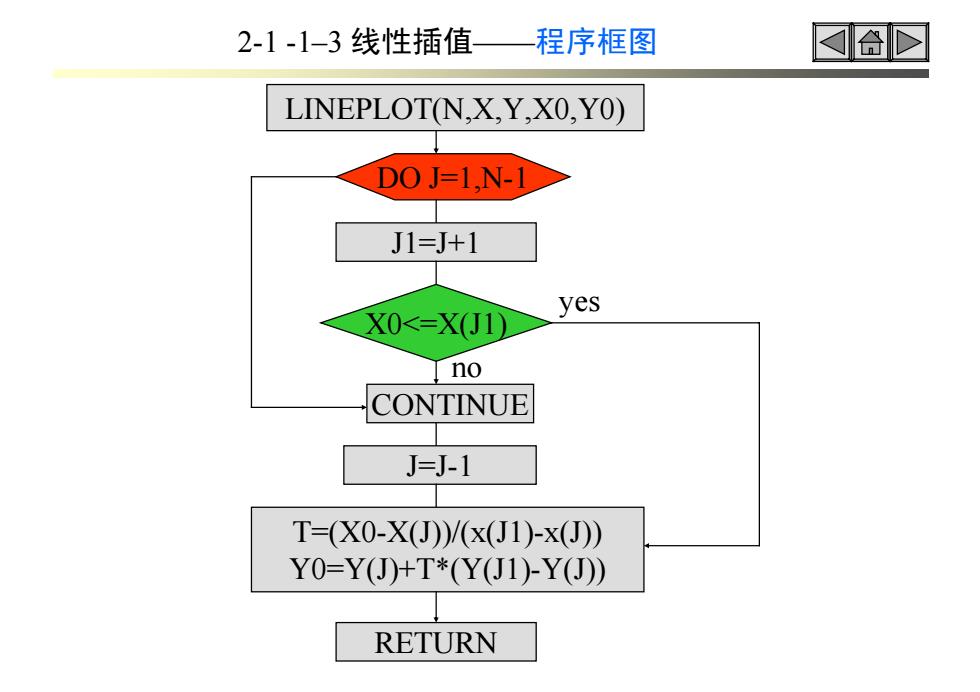
2-1-1-3线性插值 程序框图 ☑合 LINEPLOT(N.X.Y.XO,YO) DOJ=1,N-1> J1=J+1 yes X0<=X(J1) no CONTINUE J=J-1 T=(X0-X(J)/(x(J1)-x(J) YO=Y(J)+T*(Y(J1)-Y(J)) RETURN
LINEPLOT(N,X,Y,X0,Y0) DO J=1,N-1 J1=J+1 X0<=X(J1) CONTINUE J=J-1 T=(X0-X(J))/(x(J1)-x(J)) Y0=Y(J)+T*(Y(J1)-Y(J)) RETURN no yes 2-1 -1–3 线性插值——程序框图
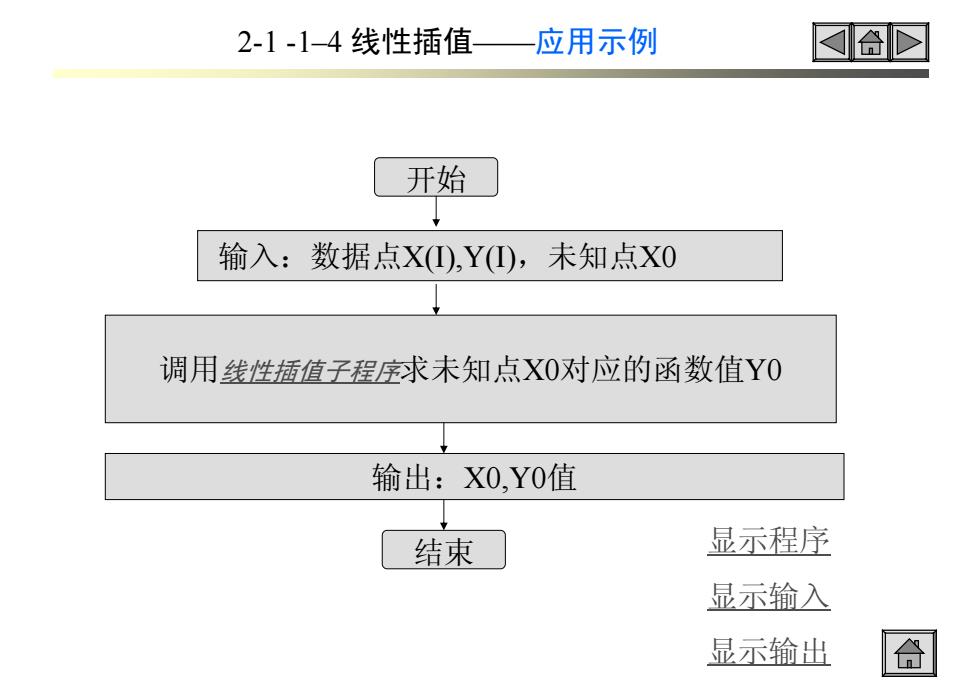
2-1-1-4线性插值 应用示例 合D 开始 输入:数据点X①,Y(①,未知点X0 调用线性插值子程序求未知点X0对应的函数值Y0 输出:X0,Y0值 结束 显示程序 显示输入 显示输出 合
开始 输入:数据点X(I),Y(I),未知点X0 调用线性插值子程序求未知点X0对应的函数值Y0 输出:X0,Y0值 结束 2-1 -1–4 线性插值——应用示例 显示程序 显示输入 显示输出
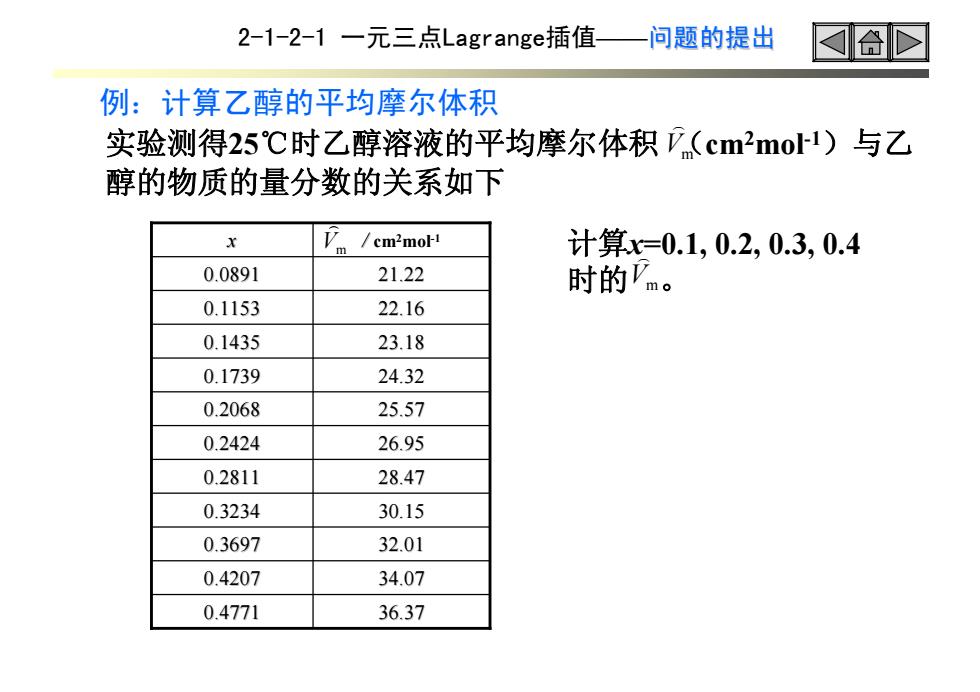
2-1-2-1一元三点Lagrange插值 问题的提出 合D 例:计算乙醇的平均摩尔体积 实验测得25℃时乙醇溶液的平均摩尔体积,(cmmo1)与乙 醇的物质的量分数的关系如下 x m /cm2mol1 计算x=0.1,0.2,0.3,0.4 0.0891 21.22 时的Vm。 0.1153 22.16 0.1435 23.18 0.1739 24.32 0.2068 25.57 0.2424 26.95 0.2811 28.47 0.3234 30.15 0.3697 32.01 0.4207 34.07 0.4771 36.37
2-1-2-1 一元三点Lagrange插值——问题的提出 例:计算乙醇的平均摩尔体积 实验测得25℃时乙醇溶液的平均摩尔体积 (cm 2mol-1)与乙 醇的物质的量分数的关系如下 0.4771 36.37 0.4207 34.07 0.3697 32.01 0.3234 30.15 0.2811 28.47 0.2424 26.95 0.2068 25.57 0.1739 24.32 0.1435 23.18 0.1153 22.16 0.0891 21.22 / cm2mol-1 x 计算x=0.1, 0.2, 0.3, 0.4 时的 。 Vm ) Vm ) Vm )