
第四章本(特)征值和本(特)征向量 国合正 化学中的本征值和本征向量问题与量子化学的发展密切相关。 求实对称矩阵的本征值和本征向量以及广义本征值和本征向量 是分子轨道近似计算方法中最主要的一步。 本征值和本征向量的定义: n×n阶方阵,存在 (A-I)X=0i.e.Ax=λx 入一A的本征值 非零解x一与本征值对应的本征向量
第四章 本(特)征值和本(特)征向量 化学中的本征值和本征向量问题与量子化学的发展密切相关。 求实对称矩阵的本征值和本征向量以及广义本征值和本征向量 是分子轨道近似计算方法中最主要的一步。 本征值和本征向量的定义: 本征值和本征向量的定义: n × n阶方阵,存在 ( A − λI ) X = 0 i.e. Ax = λx λ——A的本征值 非零解 x——与本征值 λ对应的本征向量

4-1问题的提出 合 Huckel分子轨道法:共轭分子 Schroedinger方程: Aw=Ew 原子轨道线性组合(LCAO): w=∑C,4 wvdr=∫Evdr E E=f(C,C2…Cn) yydr 存在的稳定体系符合能量最低原理。根据变分原理, =0 ac (i=1,2,3,…,n) 通常把波函数选成实函数 yHydr E w'dr
4-1 问题的提出 Hückel分子轨道法:共轭分子 Schroedinger方程: Hˆψ = Eψ 原子轨道线性组合(LCAO): ψ = ∑Ciφi ∫ ∫ ψ Hψdτ = ψ Eψdτ * * ˆ 存在的稳定体系符合能量最低原理。根据变分原理, ∫ ∫ = ψ ψ τ ψ ψ τ d H d E * * ˆ ( , ) C1 C2 Cn E = f L 0 (i 1,2,3, ,n) CEi = = L ∂∂ 通常把波函数选成实函数 ∫ ∫ = ψ τ ψ ψ τ d H d E 2 ˆ
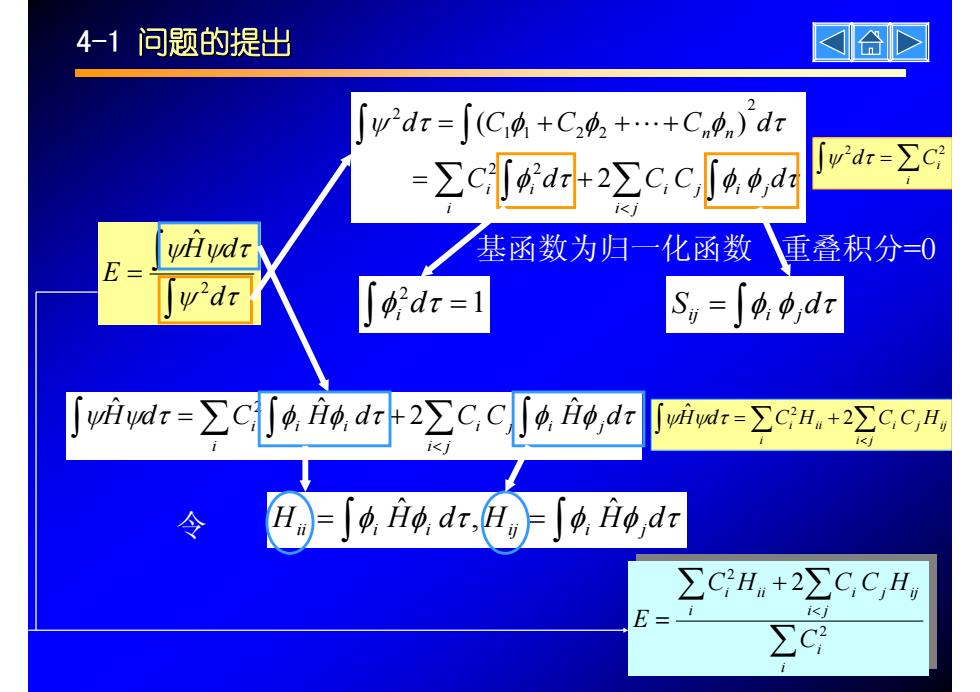
4-1问题的提出 国合> w2dr=「(C+C22+…+Cnpn)dx =∑cd+2∑c,c「4d wdr=∑c 基函数为归一化函数 重叠积分=0 E w'dr 好dr=1 S,=00,dr whvdr=∑cJio,dr+2∑C,C打4ip,dr wHwdr=∑CH+2∑C,C,H i< t<l 令 4Hdr,日∫,ip,dr ∑CHn+2∑C,C,H E=- i<j ∑c
∑ ∫ ∑ ∫ ∫ ∫ < = + = + + + φ τ φ φ τ ψ τ φ φ φ τ C d C C d d C C C d i j i j i j i i i n n 2 ( ) 2 2 2 1 1 2 2 2 L 基函数为归一化函数 重叠积分=0 1 2 = ∫φ dτ i ∫ S = φ φ dτ ij i j ∫ = ∑ i d Ci 2 2 ψ τ ∫ ∑ ∫ ∑ ∫ < ψHψdτ = C φ Hφ dτ + C C φ Hφ dτ i j i j i j i i i i ˆ 2 ˆ ˆ 2 令 ∫ ∫ H = φ Hφ dτ H = φ Hφ dτ ii i i ij i j ˆ , ˆ ij i j i j i ∫ H d ∑Ci Hii ∑C C H < = + 2 ˆ 2 ψ ψ τ 4-1 问题的提出 ∫ ∫ = ψ τ ψ ψ τ d H d E 2 ˆ ∑ ∑ ∑ < + = i i ij i j i j i i ii C C H C C H E 2 2 2

4-1问题的提出 国合心 wHydz E ∑CHm+2∑C,C,H v'dr E二 i<j ∑c网 OE =0 ac (i=1,2,3,…,n) C1(H1-E)+C2H12+…+CnHn=0 C1H21+C2(H22-E)+…+CnH2n=0 (A-I)X=0 CHn+C2H2+.+Cn(Hm-E)=0 (H-ED)C=0 (久期方程式) 本征值配:所求体系的单电子分子轨道的能量,可用来确定 这些轨道的能级次序,导出的它们电子构型以及分子的总状态。 单电子轨道能量数值本身也可用来估计分子的某些性质,如 分子的电离势、电跃迁能量等。 本征向量℃:其数值与分子中电子密度的分布以及各个原于 的有效电荷相关联。它们决定了分子体系的一系列物理性质, 如偶极矩等
∫ ∫ = ψ τ ψ ψ τ d H d E 2 ˆ ∑ ∑ ∑ < + = i i ij i j i j i i ii C C H C C H E 2 2 2 0 (i 1,2,3, ,n) CEi = = L ∂∂ ( ) 0 ( ) 0 ( ) 0 1 1 2 2 1 21 2 22 2 1 11 2 12 1 + + + − = + − + + = − + + + = C H C H C H E C H C H E C H C H E C H C H n n n nn n n n n L LL L L ((HH-EI -EI))CC=0=0 (A− λI)X = 0 本征值E:所求体系的单电子分子轨道的能量,可用来确定 这些轨道的能级次序, 导出的它们电子构型以及分子的总状态。 单电子轨道能量数值本身也可用来估计分子的某些性质,如 分子的电离势、电跃迁能量等。 (久期方程式) 本征向量Cj:其数值与分子中电子密度的分布以及各个原于 的有效电荷相关联。它们决定了分子体系的一系列物理性质, 如偶极矩等。 4-1 问题的提出

4.2方法原理 国合心 1,行列式求值法 (A-)X=0 齐次联立方程组 |A-I=0 时,此联立方程组有非平凡解X≠0 1 2 例:求下列矩阵的本征值和本征向量: A三 -1 -入 2 A-I月 =0 2 -1- 本征方程 (1-2)(-1-)-4=0 本征值 2=±V5 代入原方程可解出本征向量X
4.2 方法原理 1.行列式求值法 (A− λI)X = 0 例:求下列矩阵的本征值和本征向量: ⎥⎦⎤ ⎢⎣⎡ − = 2 1 1 2 A 0 2 1 1 2 | | =⎥⎦⎤ ⎢⎣⎡ − − − − = λ λ A λI 本征方程 (1− λ)(−1− λ) − 4 = 0 本征值 λ = ± 5 齐次联立方程组 | A − λI |= 0 时,此联立方程组有非平凡解X≠0 代入原方程可解出本征向量X

4.2方法原理 合区 2.Jacobi方法求实对称矩阵的本征值和本征向量 基本思想: 通过一组平面旋转变换(正交相似变换),将实对称 矩阵A化为对角矩阵。 对角矩阵中对角线上的元素几即为本征值; 每一步的平面旋转矩阵的乘积的第列即为几对应的本征向量。 正交变换矩阵: cose -sin 1 sin0 cos0
4.2 方法原理 2.Jacobi 2.Jacobi方法求实对称矩阵的本征值和本征向量 方法求实对称矩阵的本征值和本征向量 基本思想: 通过一组平面旋转变换(正交相似变换),将实对称 矩阵A化为对角矩阵。 对角矩阵中对角线上的元素λi即为本征值; 每一步的平面旋转矩阵的乘积的第i列即为λi对应的本征向量。 ⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤ ⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡ − = 1 1 sin cos 1 1 cos sin 1 1 1 O O O θ θ θ θ T i i j j 正交变换矩阵:

4.2方法原理 国合正 a12 a13 0 d21 022 a23 a2n an2 an3 0 Ak =TkAk-T lim A D k→00 D= 本征值 TT,I3…Tk=' 各列向量是A的各个本征值的本征向量 V-AVK=D
[ ] n k k k k k k D A D A T A T λ ,λ ,λ ,Lλ lim 1 2 3 1 1 = = = →∞ − − ——本征值 T1T2T3LTk =Vk ——各列向量是A的各个本征值的本征向量 AV V D V AV D k k k k = = −1 4.2 方法原理 ⎥⎥⎥⎥⎦⎤ ⎢⎢⎢⎢⎣⎡ ⎯⎯→ ⎥⎥⎥⎥⎦⎤ ⎢⎢⎢⎢⎣⎡ n n n nn n nn a a a a a a a a a a a a λ λ λ 0 0 2 1 1 2 3 21 22 23 2 11 12 13 1 O L L LL

4.3应用示例 合区 例1丁二烯的HMO处理。 丁二烯(HC=CH一CH=CH,) 的分子轨道为 w=C141+C2p2+C34+C4p4 按变分法及基本假设,C满足久期方程组 a-E B 0 0 C B a-E B 0 C2 0 0 a-E C; 0 0 0 B a-E Ca 0 x=(a-E)/B 0 0 1 0 C. 1 x C 00 0 01 xC.] 0 久期行列式 x10 0 01x 001x
4.3 应用示例 例1丁二烯的HMO处理。 x = (α − E)/ β 久期行列式 丁二烯(H2C=CH—CH=CH2)的分子轨道为 ψ = C1φ1 + C2φ 2 + C3φ 3 + C4φ 4 按变分法及基本假设,Cj满足久期方程组 ⎥⎥⎥⎥⎦⎤ ⎢⎢⎢⎢⎣⎡ =⎥⎥⎥⎥⎦⎤ ⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤ ⎢⎢⎢⎢⎣⎡ − − − − 0000 0 0 0 0 0 0 4321 CCCC E E E E β α β α β β α β α β ⎥⎥⎥⎥⎦⎤ ⎢⎢⎢⎢⎣⎡ =⎥⎥⎥⎥⎦⎤ ⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤ ⎢⎢⎢⎢⎣⎡ 0000 0 0 1 0 1 1 1 1 0 1 0 0 4321 CCCC x x x x 0 0 0 1 0 1 1 1 1 0 1 0 0 = x x x x

4.3应用示例 国合正 即 x4-3x2+1=0 解之,得…x1=0.618x2=-0.6183=1.618x4=-1.618 所以 E1=a-0.618B,E2=a+0.618p, E3=a-1.6186,E4=a+1.6180 1,E2,E3,E4分别是4个不同x值得到的离域π键的4个分子轨道能级。¥ 总的π电子能量为En=E1+E2+E3+E4=4a+
4.3 应用示例

4.3应用示例 国合心 结合归一化条件C+C+C+C=1,还可从每个x值得到与其能级相应的分子轨道函数的系数。 例如,由x4=1618代入式(4-6),得 「-1.618 1 0 0 C 0 1 -1.618 1 0 C2 0 0 1 -1.618 1 0 0 0 1 -1.618 0 整理上式,可得到…C1=C4,C2=C3 代入归-化条件得C+1.618C1)2+1.618C1)2+C2=1 即…C1=0.372 取C1=C4=0.372,C2=C3=0.602,则对应于E4=a+1.618B的分子轨道波函数为+ Ψ=0.3724+0.60202+0.602C343+0.37204
4.3 应用示例