
北京化工大学2007一一2008学年第一学期 《计算化学》期末考试试卷标准答案 第一部分填空题 (共30分,1,2,12-14每空0.5分,其余每空1分) 1.化学学科、数学学科、计算机学科 2.(1)对所要解决的问题进行分析,将化学问题转变为数学模型,选择合 适的计算方法:(2)写出解决问题的程序。(3)代码程序的编写:(4)程序的 设计和编译:(5)试算分析,输出结果 3.(1)函数fx)在区间[a,b]内连续,(2)函数在a、b两点之值a)与b)异 号:压力对化学反应中反应物平衡转化率的影响。 4.差商。 5.(1)选主元:(2)消元:(3)回代。 6.(1)插值法:(2)回归分析:函数:相关。 7.相关系数:R= Lo F1 8.复化求积:(1)用插值程序求任意点的函数值。(2)用Simpson求积程 序计算[a,b]区间中离散点下的面积。 9.一系列离散点:y=F(x),F(x)为原函数:化学动力学 10.分子轨道。 11,反射、收缩、扩张 12.随机数:牛顿运动。 13.Chemwindow/Chem Office,Origin,Gaussian,Materials studio. 14.统计法调优、模拟法调优
1 北京化工大学 2007——2008 学年第一学期 《计算化学》期末考试试卷标准答案 第一部分 填空题 (共 30 分,1,2,12-14 每空 0.5 分,其余每空 1 分) 1.化学学科、数学学科、计算机学科。 2.(1)对所要解决的问题进行分析,将化学问题转变为数学模型,选择合 适的计算方法;(2)写出解决问题的程序。(3)代码程序的编写;(4)程序的 设计和编译;(5)试算分析,输出结果。 3.(1)函数 f(x)在区间[a,b]内连续,(2)函数在 a、b 两点之值 f(a)与 f(b)异 号;压力对化学反应中反应物平衡转化率的影响。 4.差商。 5.(1)选主元;(2)消元;(3)回代。 6.(1)插值法;(2)回归分析;函数;相关。 7.相关系数; ( )1 2 xx yy xy L L L R = ;1。 8.复化求积;(1)用插值程序求任意点的函数值。(2) 用 Simpson 求积程 序计算[a,b]区间中离散点下的面积。 9.一系列离散点; y = F(x) , F(x)为原函数;化学动力学 10.分子轨道。 11.反射、收缩、扩张 12.随机数;牛顿运动。 13.Chemwindow/Chem Office ,Origin,Gaussian,Materials studio。 14.统计法调优、模拟法调优

第二部分上机题(共70分) P 1.计算原理(化学原理和计算方法)(15分) 标准平衡常数与温度关系的经验方程式为: InK=ao++a:InT+aT+aT2+asT (5分) 将表中所列实验数据代入多元线性回归子程序(其中调用高斯消去法子程 序解正规方程组),通过计算确定方程中的各个系数ao、a1、a2、a3、a4、a5值和 复相关系数。(5分) 通过计算的a、a、a2、a、a4、as值得到标准平衡常数与温度的关系式, 将T=673.2K代入关系式中计算673.2K时反应的标准平衡常数。(5分) 2程序框图(20分) 开始 输入:数据点数N 标准平衡常数与温度的数据K()、T()(4分) y=hk,=7=h7,=7,=T,本=T34分 调用多元线性回归子程序计算回归方程的系数ao、a、a2、a、a4、a值 及复相关系数R(4分) T=673.2K代入关系式中计算K632(4分) 输出:a、a、a2、a、a4、a5值、R、K673.2(4分) 结束
2 第二部分 上机题(共 70 分) A 1.计算原理(化学原理和计算方法)(15 分) 标准平衡常数与温度关系的经验方程式为: 3 5 2 2 3 4 1 0 ln a lnT a T a T a T T a K = a + + + + + θ (5 分) 设 3 5 2 1 2 3 4 , ln , , , 1 ln , x T x T x T x T T y = K x = = = = = θ 将表中所列实验数据代入多元线性回归子程序(其中调用高斯消去法子程 序解正规方程组),通过计算确定方程中的各个系数 a0、a1、a2、a3、a4、a5 值和 复相关系数。(5 分) 通过计算的 a0、a1、a2、a3、a4、a5 值得到标准平衡常数与温度的关系式, 将 T=673.2K 代入关系式中计算 673.2K 时反应的标准平衡常数。(5 分) 2.程序框图(20 分) 开始 输入:数据点数 N, 标准平衡常数与温度的数据 K(I)、T(I)(4 分) 调用多元线性回归子程序计算回归方程的系数 a0、a1、a2、a3、a4、a5 值 及复相关系数 R (4 分) 输出:a0、a1、a2、a3、a4、a5 值、R、K673.2 (4 分) 结束 3 5 2 1 2 3 4 , ln , , , 1 ln , x T x T x T x T T y = K x = = = = = θ (4 分) T=673.2K 代入关系式中计算 K673.2(4 分)

3.源程序(20分) (10分) dimension XV(11).S(11).T(8).K0(8) COMMON /AX/A(10,11).X(10,10 OPEN(5,FI 2008T I.TXT,STATUS -OLD) 2008TA2.TXT,STATUS-UNKNOWN) M1= READ(5.)(T(D),K0(D).1=1N) X(L5) KTIEXP(KK) AONIY-TEAGNUPTI-THAGMIPTI-TTI 20 FORMATU4X'INPUT DATAXL'IXX2.1x.Xnm.Yn(m=L'& DO40=N VCALC-BO D030J=1,M 30 DIPF-YCAICNOAIC-AUMINU) 8 WRITE(6.50)(X(IJ)J=1.MI).YCALC.DIFF FORMATGX10G104) WRITE(6.60)(XV(D.I=1.MI) 60 FORMATUIX.XY.10G10.4) wRTE6.70)(S0.=1,MI) 70 FORMATU/IX.'SV.10G10.4) WRITE(6.80) 80 FORMATUSX RA ssion equation is:()) WRITE(6.90)B0.(A(L.MI).I=1.M) FORMATOX 'Ink=G104+G104T+G104InT+ G10.4,*T,4,G10.4,*T*2,+,G10.4,*T*3) WRITE(6.100)OT.U.OE.SE.U/OT.R.F 100 FORMAT(/5X.'Qt-.GI8.6/5X.U-.G18.6/5X.Qe-.G18.6/5X.& Se=G186J5X,N=,G18.65X,'R=G18.65XF=,& C1e61 WRITE(6.110)KTI 110 FORMAT(/5X.K0(673.2K)=G18.6) END
3 3.源程序(20 分) program main DOUBLE PRECISION XV,S,A,X,B0,QT,U,QE,SE,R,F,T,K0,T1,KK,KT1 (10 分) dimension XV(11),S(11),T(8),K0(8) COMMON /AX/A(10,11),X(10,10) OPEN(5,FILE='2008TA1.TXT',STATUS='OLD') OPEN(6,FILE='2008TA2.TXT',STATUS='UNKNOWN') READ(5,*) M,N M1=M+1 READ(5,*) (T(I),K0(I),I=1,N) T1=673.2 DO 15 I=1,N X(I,1)=1/T(I) X(I,2)=LOG(T(I)) X(I,3)=T(I) X(I,4)=T(I)**2 X(I,5)=T(I)**3 15 X(I,M1)=LOG(K0(I)) 16 CALL MLR(M,N,XV,S,B0,QT,U,QE,SE,R,F) KK=B0+A(1,M1)/T1+A(2,M1)*LOG(T1)+A(3,M1)*T1+A(4,M1)*T1*T1+A(5,M1)*T1*T1*T1 KT1=EXP(KK) WRITE(6,20) M,N 20 FORMAT(/4X,'INPUT DATA:','X1,'1X,'X2,....',1X,'Xnm,Yn(m=1,' & ,i2,',n=1,',i2,')'/1X,86(1H-)/6X,'X1',8X,'X2',8X, 'X3',8X,'X4',8X,'X5',8X,& 'Y',7X,'Ycalc',7X,'DIFF'/1X,86(1H-)) DO 40 I=1,N YCALC=B0 DO 30 J=1,M 30 YCALC=YCALC+A(J,M1)*X(I,J) DIFF=YCALC-X(I,M1) 40 WRITE(6,50) (X(I,J),J=1,M1),YCALC,DIFF 50 FORMAT(3X,10G10.4) WRITE(6,60) (XV(I),I=1,M1) 60 FORMAT(/1X,'Xv',10G10.4) WRITE(6,70) (S(I),I=1,M1) 70 FORMAT(/1X,'Sv',10G10.4) WRITE(6,80) 80 FORMAT(/5X,'Regression equation is:',/1x,86(1H-)) WRITE(6,90) B0,(A(I,M1),I=1,M) 90 FORMAT(1X,'lnk=',G10.4,'+',G10.4,'/T','+',G10.4,'*lnT','+', & G10.4,'*T','+',G10.4,'*T**2','+',G10.4,'*T**3') WRITE(6,100) QT,U,QE,SE,U/QT,R,F 100 FORMAT(/5X,'Qt=',G18.6,/5X,'U=',G18.6,/5X,'Qe=',G18.6,/5X, & 'Se=',G18.6,/5X,'N=',G18.6,/5X,'R=',G18.6,/5X,'F=', & G18.6) WRITE(6,110) KT1 110 FORMAT(/5X,'K0(673.2K)=',G18.6) END

SUBROUTINEMLR(M,N,XV.S,BO.QT,U.QE,SE,R,F) (5分) DOUBLEPRECISION XV.S.A,X,BO.QT,U.QE,SE,R,F DIMENSION XV(M+1),S(M+1),ALIO(50) COMMON /AX/A(10,11).X(50.10) M1=M+1 D020=1,M1 XV①=0.D0 D010K=1,N 10 XV(EXV(DH+X(KD 20 XV(I)=XV(I/DBLE(N) DO40I=1.M1 S①=0 D030K=1N 西 S(D)=S(I+(X(K,I)-XV(D))**2 40 SODDSORT(S()) D050=1,M ALIO(T)-0 DO 50 K=L.N 50 ALIO(I=ALIO(I)+(X(K,I)-XV(I))*(X(K,MI)-XV(MI)) D060=1M1 D060K=1 60 X(K.IF(X(KIXV(DVS(D) D070I=1,M AF1.0 D070 +1,M A(IJ)=0 D070 K=1,N 70 A(IJ)=A(IJ)+X(K.I)*X(K.J) D0801= M- D080 41, 80 FORMAT(4X,'Normal equation A(m,m+1),2x,'m=,i2/Ix,60(1H-)) D090I=1,M 90 CAL TE6,3)(A=1,M) A,M,M1.1.D-06 WRITE(6,22 WRITE(6,33)(A(I,MI),I=1,M) =1M *S(MI)/S(I) 100 LIO(T -SQRT(QE/(N-M-1 /QT) -1)U/QE/M
4 SUBROUTINE MLR(M,N,XV,S,B0,QT,U,QE,SE,R,F) (5 分) DOUBLE PRECISION XV,S,A,X,B0,QT,U,QE,SE,R,F DIMENSION XV(M+1),S(M+1),ALI0(50) COMMON /AX/A(10,11),X(50,10) M1=M+1 DO 20 I=1,M1 XV(I)=0.D0 DO 10 K=1,N 10 XV(I)=XV(I)+X(K,I) 20 XV(I)=XV(I)/DBLE(N) DO 40 I=1,M1 S(I)=0 DO 30 K=1,N 30 S(I)=S(I)+(X(K,I)-XV(I))**2 40 S(I)=DSQRT(S(I)) DO 50 I=1,M ALI0(I)=0 DO 50 K=1,N 50 ALI0(I)=ALI0(I)+(X(K,I)-XV(I))*(X(K,M1)-XV(M1)) DO 60 I=1,M1 DO 60 K=1,N 60 X(K,I)=(X(K,I)-XV(I))/S(I) DO 70 I=1,M A(I,I)=1.0 DO 70 J=I+1,M1 A(I,J)=0 DO 70 K=1,N 70 A(I,J)=A(I,J)+X(K,I)*X(K,J) DO 80 I=1,M-1 DO 80 J=I+1,M 80 A(J,I)=A(I,J) WRITE(6,11) M 11 FORMAT(4X,'Normal equation A(m,m+1)',2x,'m=',i2/1x,60(1H-)) DO 90 I=1,M 90 WRITE(6,33) (A(I,J),J=1,M1) CALL GS(A,M,M1,1.D-06) WRITE(6,22) WRITE(6,33) (A(I,M1),I=1,M) B0=0.D0 U=0.D0 DO 100 I=1,M A(I,M1)=A(I,M1)*S(M1)/S(I) B0=B0+A(I,M1)*XV(I) 100 U=U+A(I,M1)*ALI0(I) B0=XV(M1)-B0 QT=S(M1)*S(M1) QE=QT-U SE=DSQRT(QE/(N-M-1)) R=DSQRT(1.D0-QE/QT) F=(N-M-1)*U/QE/M

22 FORMAT(/4X.'Roots of mormal equation,'A(i,m+1).i=1,m'& 33 T1X10G12.4) END (5分) D050K=.N D-00 DO IOI-K N 1= CONTINUE IF(P.LT.EPS)STOPNO SOLUTION IF(L.EO.KXGOTO 30 DO 20J=K.M TMP=A(LJ) A(L IEAK A(K I=TMP CONTINUE P=L0/A(KK D040J=K+1M A(K JEA(K'P DO401=K+1N ALJ=AL-ALK*AKJD 40 CONTINUE 50 CONTINUE DO 60 K=2.N I=M-K D060J=+1.N A(LM=A(LM)-A(LJ)*A(.M) 60 CONTINUE RETURN END 4.运行结果。(15分》 Regression equation is 10分) 569.3 1574 +06/T+-71.89 *1nT+2.695 *T+-2696E-02*T*2+9940E-06*T* 222 Qe- 6.9116 82 K0(673.2K 411973E-03 (5分)
5 22 FORMAT(/4X,'Roots of mormal equation','A(i,m+1),i=1,m' & /1x,60(1H-)) 33 FORMAT(1X,10G12.4) RETURN END SUBROUTINE GS(A,N,M,EPS) (5 分) DOUBLE PRECISION EPS,A DIMENSION A(10,11) DO 50 K=1,N P=0.0 DO 10 I=K,N IF(P.GE.ABS(A(I,K)))GOTO 10 P=ABS(A(I,K)) L=I 10 CONTINUE IF(P.LT.EPS)STOP'NO SOLUTION' IF(L.EQ.K)GOTO 30 DO 20 J=K,M TMP=A(L,J) A(L,J)=A(K,J) A(K,J)=TMP 20 CONTINUE 30 P=1.0/A(K,K) DO 40 J=K+1,M A(K,J)=A(K,J)*P DO 40 I=K+1,N A(I,J)=A(I,J)-A(I,K)*A(K,J) 40 CONTINUE 50 CONTINUE DO 60 K=2,N I=M-K DO 60 J=I+1,N A(I,M)=A(I,M)-A(I,J)*A(J,M) 60 CONTINUE RETURN END 4.运行结果。(15 分) Regression equation is: -------------------------------------------------------------------------------------- (10 分) lnk=-669.3 + .1574E+06/T+-71.89 *lnT+ 2.695 *T+-.2696E-02*T**2+ .9940E-06*T**3 Qt= 2232.81 U= 2225.90 Qe= 6.91162 Se= 1.85898 N= .996905 R= .998451 F= 128.821 K0(673.2K)= .411973E-03 (5 分)

B 1 计算原理(化学原理和计算方法)(15分) 对于双组分简单精馏塔,其精馏段和提馏段的理论板数均可用Lewis法计 算。 N= dx 4年y-x-(x-y)/R (1) M-y-x)R dx (2) 其中N和M分别表示精馏段和提馏段的塔板数:xD、xF和xw分别表示塔 顶、进料和塔釜液的物质的量分数:R和R'分别表示精馏段和提馏段的回流比: x和y分别表示汽液平衡时液相和气相的组成。(5分) (1)、(2)式右侧的定积分值,等于积分区间内被积函数曲线与x轴之间的面积,按 1 1 题中表所列数据,计算 y-x-(o-)/R和y-x-Oy-)/R的值. (5分) 根据离散点求积的方法即:用Simpson求积方法(其中调用Lagrange插值法子程序计 算任意点的函数值)计算可得到(1)和(2)式的积分S1、S2,得到精馏段和提馏段的 塔板数N和M,然后计算总的塔板数SW SN=N+M (5分) 程序框图(20分) 开始 输入:数据点数,EPS,R1,R2,XA①,YA(I)(I=1,N),XD,XF,XW(5分) Al=XF,BI=XD,A2=XW,B2=XF, (5分) 调用Simpson法子程序计算积分Sl、S2 (用插值法计算函数值),总塔板数SW=S1+S2 (7分) 6
6 B 1. 计算原理(化学原理和计算方法)(15 分) 对于双组分简单精馏塔,其精馏段和提馏段的理论板数均可用 Lewis 法计 算。 ∫ − − − = D F ( )/ d D x x y x x y R x N (1) ∫ − − − ′ = F W ( )/ d w x x y x y x R x M (2) 其中 N 和 M 分别表示精馏段和提馏段的塔板数;xD、xF 和 xW分别表示塔 顶、进料和塔釜液的物质的量分数;R 和 R’分别表示精馏段和提馏段的回流比; x 和 y 分别表示汽液平衡时液相和气相的组成。(5 分) (1)、(2)式右侧的定积分值,等于积分区间内被积函数曲线与 x 轴之间的面积,按 题中表所列数据,计算 y x (x y)/ R 1 − − D − 和 y − x − ( y − x ) / R′ 1 w 的值。 (5 分) 根据离散点求积的方法即:用 Simpson 求积方法(其中调用 Lagrange 插值法子程序计 算任意点的函数值)计算可得到(1)和(2)式的积分 S1、S2,得到精馏段和提馏段的 塔板数 N 和 M,然后计算总的塔板数 SN SN=N+M (5 分) 2. 程序框图(20 分) 开始 输入:数据点数,EPS,R1,R2,XA (I), YA(I)(I=1,N),XD,XF,XW (5 分) A1=XF, B1= XD, A2=XW, B2= XF, (5 分) 调用 Simpson 法子程序计算积分 S1、S2 (用插值法计算函数值),总塔板数 SN=S1+S2 (7 分) )

输出:总塔板数SW (3分) 结束 3· 源程序(20分) PRogram MAIN (10分) ,A2,B2,X,Y,Y1,Y2,S1,S2,R1,R2,SN 178.0.2 00 B2-0 R1=5.0 R2=40 10 CALL SOD-XO) SN-S14S2 VRE6.20) SI S2 SN 20 FORMAT(IX.S1-.5X.F6.2.5X.'S2-,G12.6//5X,THE NUMBEROFTHEORETICALPLATES-.G12.6) END SUBROUTINE SIMPIMA BX YEPS S2) (5分) DOUBLEPRECISIONA,B.X.Y.EPS.S2.FA.FB.X0,Y0 DIMENSION X(M).Y(M) H=B-A N=I CALL LGRG2CX YMA FA) CALLLGRG2(X.Y.M.B.FB) TI=0.5*H*(FA+FB) 10 g=0 D020K=1.N X0=A4K.051*I CALLLGRG2(X.Y.M.X0.Y0) 20 =g+y0 T2=05T14H 92=T2+T2.T1V30 IF(N.EQ.D)GOTO 40 0 D=ABS(S2-S1) IF(ABS(S2)GT LO)THEN 7
7 3. 源程序(20 分) PROGRAM MAIN (10 分) DOUBLE PRECISION EPS,A1,B1,A2,B2,X,Y,Y1,Y2,S1,S2,R1,R2,SN DIMENSION X(6),Y(6), Y1(6), Y2(6) N=6 EPS=1.0E-4 OPEN(6,FILE='2008TESTB1.Txt',STATUS='UNKNOWN') DATA X/0.178,0.275,0.372,0.456,0.650,0.844/ DATA Y/0.243,0.382,0.518,0.616,0.795,0.931/ A1=0.4 B1=0.9 A2=0.15 B2=0.4 R1=5.0 R2=4.0 DO 10 I=1,N Y1(I)=1/(Y(I)-X(I)-(0.9-Y(I))/R1) 10 Y2(I)=1/(Y(I)-X(I)-(Y(I)-0.15)/R2) CALL SIMP(N,A1,B1,X,Y1,EPS,S1) CALL SIMP(N,A2,B2,X,Y2,EPS,S2) SN=S1+S2 WRITE(6,20) S1,S2,SN 20 FORMAT(1X,'S1=',5X,F6.2,5X,'S2=',G12.6,//5X,'THE NUMBER OF THEORETICAL PLATES =',G12.6) END SUBROUTINE SIMP(M,A,B,X,Y,EPS,S2) (5 分) DOUBLE PRECISION A,B,X,Y,EPS,S2,FA,FB,X0,Y0 DIMENSION X(M),Y(M) H=B-A N=1 CALL LGRG2(X,Y,M,A,FA) CALL LGRG2(X,Y,M,B,FB) T1=0.5*H*(FA+FB) 10 S=0 DO 20 K=1,N X0=A+(K-0.5)*H CALL LGRG2(X,Y,M,X0,Y0) 20 S=S+Y0 T2=0.5*(T1+H*S) S2=T2+(T2-T1)/3.0 IF(N.EQ.1)GOTO 40 30 D=ABS(S2-S1) IF(ABS(S2).GT.1.0)THEN 输出:总塔板数 SN (3 分) 结束

D=AB(S2-S1)/S2) END IF IF(D.LT.EPS)GOTO50 0 N-N+N H=0.5*H T1=T2 S1=S2 G0T010 RETURN END SUBROUTINE LGRG2(X,Y.N,T.Z) (5分) DIMENSION X(N).Y(N) DOUBLE PRECISION X.Y.TZ.S Z=0.0 IF(N.LE.0)RETURN IF(N.EQ.1)THEN Z=Y1) RETURN ENDIF IF(N.EQ.2)THEN Z=Y()(T-X(2)-Y(2)(T-X(D(X(1)-X(2)) RETURN END IF IF(T.LE.X(2))THEN K M=3 ELSE IF(T.GE.X(N-1))THEN K=N- M-N M=N 10 IF(IABS(K-M).NE.1)THEN L+MW2 IF(T.LT.X(L))THEN ELS S(T-X(K)).LT.ABS(T-X(M)))THEN ELSEK-I M+I END IE
8 D=ABS((S2-S1)/S2) END IF IF(D.LT.EPS)GOTO 50 40 N=N+N H=0.5*H T1=T2 S1=S2 GOTO 10 50 RETURN END SUBROUTINE LGRG2(X,Y,N,T,Z) (5 分) DIMENSION X(N),Y(N) DOUBLE PRECISION X,Y,T,Z,S Z=0.0 IF(N.LE.0)RETURN IF(N.EQ.1)THEN Z=Y(1) RETURN END IF IF(N.EQ.2)THEN Z=(Y(1)*(T-X(2))-Y(2)*(T-X(1)))/(X(1)-X(2)) RETURN END IF IF(T.LE.X(2))THEN K=1 M=3 ELSE IF(T.GE.X(N-1))THEN K=N-2 M=N ELSE K=1 M=N 10 IF(IABS(K-M).NE.1)THEN L=(K+M)/2 IF(T.LT.X(L))THEN M=L ELSE K=L ENDIF GOTO 10 END IF IF(ABS(T-X(K)).LT.ABS(T-X(M))) THEN K=K-1 ELSE M=M+1 END IF END IF Z=0.0 DO 30 I=K,M

D0-M 20 7- END 4.运行结果(15分) S1 4.23 S2=5.20615 (10分) THE NUMBER OF THEORETICAL PLATES=9.43671 (5分) C 1.计算原理(化学原理和计算方法)(15分) 在管式反应器中进行液相吸热反应: A→R+S 已知其管内温度(T)与反应物的转化率(xA)的关系为 dT =-650-1587-Z}K k (1) 式中,速率常数k=后 其中,A=1.17×10”min, E。=1.84×10Jmol,气体常数R=8.314Jmol-1K,反应管外油浴温度(T) 恒定为613K。T为管内反应温度,入口温度为613K,反应器出口转化率为90%。 欲计算转化率变化时,管式反应器内温度的变化,需对微分方程(1)进行 求解,这是一个常微分方程的初值问题: =-65.0-15.82yK (10分) dx T=T(x4o)=613K 9
9 S=1.0 DO 20 J=K,M IF(J.NE.I)THEN S=S*(T-X(J))/(X(I)-X(J)) END IF 20 CONTINUE Z=Z+S*Y(I) 30 CONTINUE RETURN END 4. 运行结果(15 分) S1= 4.23 S2= 5.20615 (10 分) THE NUMBER OF THEORETICAL PLATES = 9.43671 (5 分) C 1.计算原理(化学原理和计算方法)(15 分) 在管式反应器中进行液相吸热反应: A ⎯⎯→R + S 已知其管内温度(T)与反应物的转化率(xA)的关系为 { 65.0 15.8 } K d d c A k T T x T − = − − (1) 式中,速率常数 17 1 , 1.17 10 min − − k = Ae A = × RT Ea 其中, , 5 -1 = 1.84×10 J⋅ mol Ea ,气体常数 R=8.314 J·mol-1 ·K-1,反应管外油浴温度(Tc) 恒定为 613K。T 为管内反应温度,入口温度为 613K,反应器出口转化率为 90%。 欲计算转化率变化时,管式反应器内温度的变化,需对微分方程(1)进行 求解,这是一个常微分方程的初值问题: { 65.0 15.8 } K d d c A k T T x T − = − − (10 分) K T0 = T(xA0 ) = 613
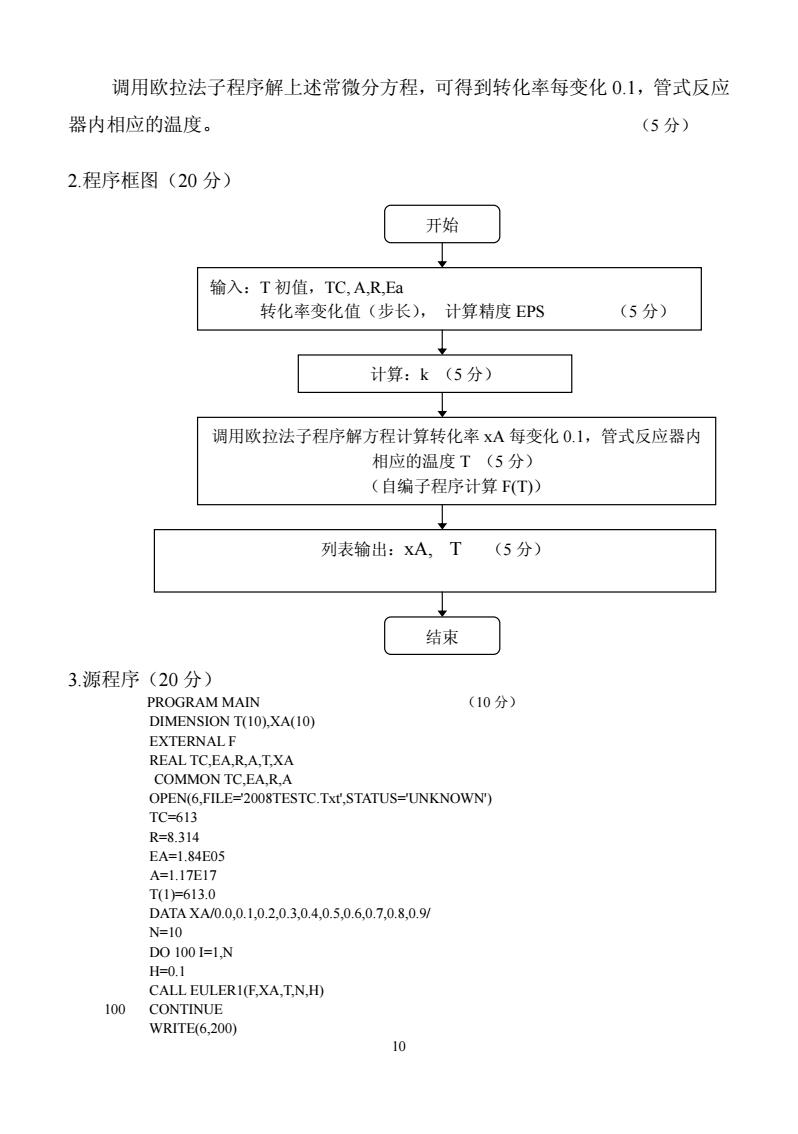
调用欧拉法子程序解上述常微分方程,可得到转化率每变化0.1,管式反应 器内相应的温度。 (5分) 2.程序框图(20分) 开始 输入:T初值,TC,A,R,Ea 转化率变化值(步长),计算精度EPS (5分) 计算:k(5分) 调用欧拉法子程序解方程计算转化率xA每变化0.1,管式反应器内 相应的温度T(5分) (自编子程序计算F(T) 列表输出:xA,T (5分) 结束 3.源程序(20分) (10分) EXTERNAL F REAL TC.EA,R A.TXA TC,EA,R,A 6.FILE-2008TESTC.Txr.STATUS-UNKNOWN) TC .314 1.84 A .17 DAAM0aou020304050607080gy 100 6,200)
10 调用欧拉法子程序解上述常微分方程,可得到转化率每变化 0.1,管式反应 器内相应的温度。 (5 分) 2.程序框图(20 分) 3.源程序(20 分) PROGRAM MAIN (10 分) DIMENSION T(10),XA(10) EXTERNAL F REAL TC,EA,R,A,T,XA COMMON TC,EA,R,A OPEN(6,FILE='2008TESTC.Txt',STATUS='UNKNOWN') TC=613 R=8.314 EA=1.84E05 A=1.17E17 T(1)=613.0 DATA XA/0.0,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9/ N=10 DO 100 I=1,N H=0.1 CALL EULER1(F,XA,T,N,H) 100 CONTINUE WRITE(6,200) 开始 输入:T 初值,TC, A,R,Ea 转化率变化值(步长), 计算精度 EPS (5 分) 计算:k (5 分) 调用欧拉法子程序解方程计算转化率 xA 每变化 0.1,管式反应器内 相应的温度 T (5 分) (自编子程序计算 F(T)) 列表输出:xA, T (5 分) 结束