
第七章化学化工中的计算机模拟简介 合店 化学物系结构和运动的模拟 Monte Carlo方法 借计算机之助取样以求高维积分数值的技术。是一种统计 模拟方法。 不要求将模型过分简化,可以基于分子(原 子、离子)的排列和运动的模拟结果直接计算求和,以实现 宏观现象中数量的估算。 分子动力学方法(Molecular dynamics method) 将系统运动方程组数值积分,得到个经典粒子系统的 相轨道,进而研究该系统的平衡热力学性质,结构动力 学性质、非平衡输运性质等。 化工过程模拟
第七章 化学化工中的计算机模拟简介 Monte Carlo方法 借计算机之助取样以求高维积分数值的技术。是一种统计 模拟方法。 不要求将模型过分简化,可以基于分子(原 子、离子)的排列和运动的模拟结果直接计算求和,以实现 宏观现象中数量的估算。 分子动力学方法(Molecular dynamics method) 将系统运动方程组数值积分,得到N个经典粒子系统的 相轨道,进而研究该系统的平衡热力学性质,结构动力 学性质、非平衡输运性质等。 化工过程模拟 化学物系结构和运动的模拟
7-1 Monte Carlo方法 应用示例 高分子热降解的Monte Carlo法模拟 为了研究耐热塑料,需要探讨塑料的高分子结构和耐热 性的关系。用双链高分子代替单链高分子即采取“梯状” 高分子结构,是提高塑料耐热性一条可能的途径。多骈 六元环或多骈四元环可以构成梯状高分子的骨架
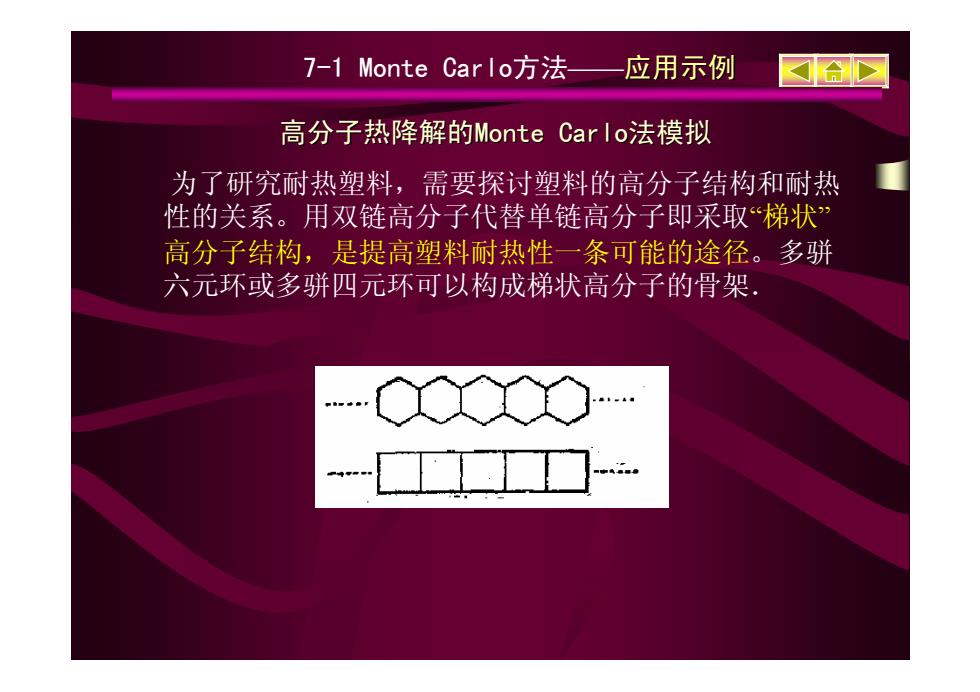
高分子热降解的 高分子热降解的Monte Carlo Monte Carlo法模拟 7-1 Monte Carlo方法——应用示例 为了研究耐热塑料,需要探讨塑料的高分子结构和耐热 性的关系。用双链高分子代替单链高分子即采取“梯状” 高分子结构,是提高塑料耐热性一条可能的途径。多骈 六元环或多骈四元环可以构成梯状高分子的骨架.
7-1 Monte Carlo方法 应用示例 合店 Tessler用Monte Carlo法研究了由六元环或四元环骈合 而成的梯状高分子的随机热降解过程。 起始 发生随机数 000 00 记录 另一测 简单机理列 架希机是列 降长高分子障解机逆 商单机理的降解棋以震图
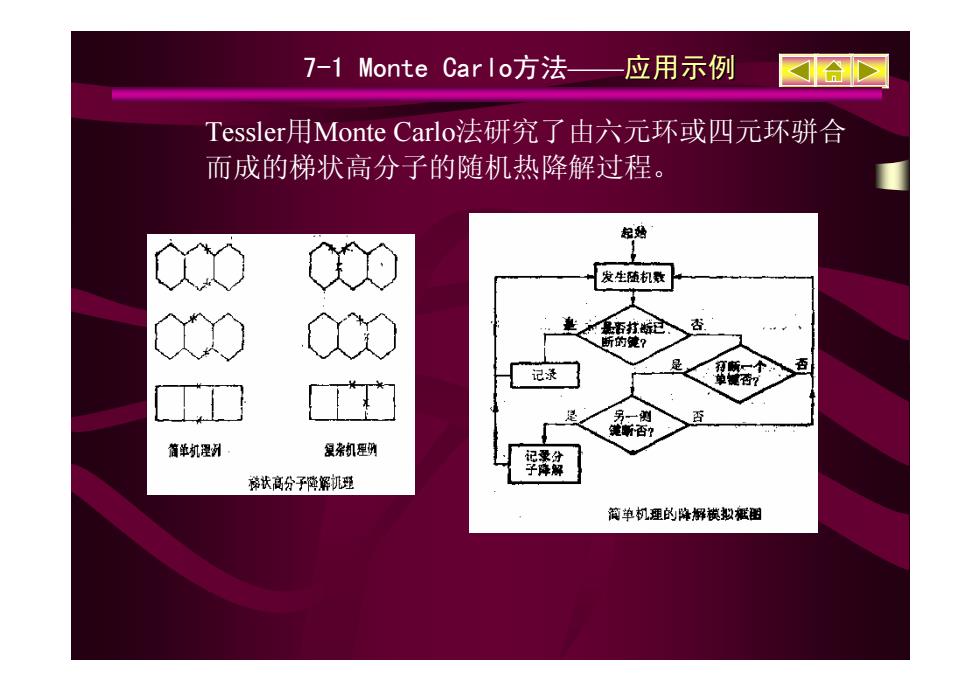
Tessler用Monte Carlo法研究了由六元环或四元环骈合 而成的梯状高分子的随机热降解过程。 7-1 Monte Carlo方法——应用示例
7-1 Monte Carlo方法 应用示例 K合区 Tessler的模拟结果表明:梯状高分子降解速率比 单键高分子小很多。无论是按简单降解机理还是复杂降解 机理,梯状高分子的热稳定性都比单链高分子好。若梯状 高分子有结构缺陷”,即某些局部有悬键的情况,则降解 的诱导期变短,降解加快。 0.1 2,0净 国6 稀状高分子的降解率与单链高分子的比较 1.简单机理2.复杂机里3,单链
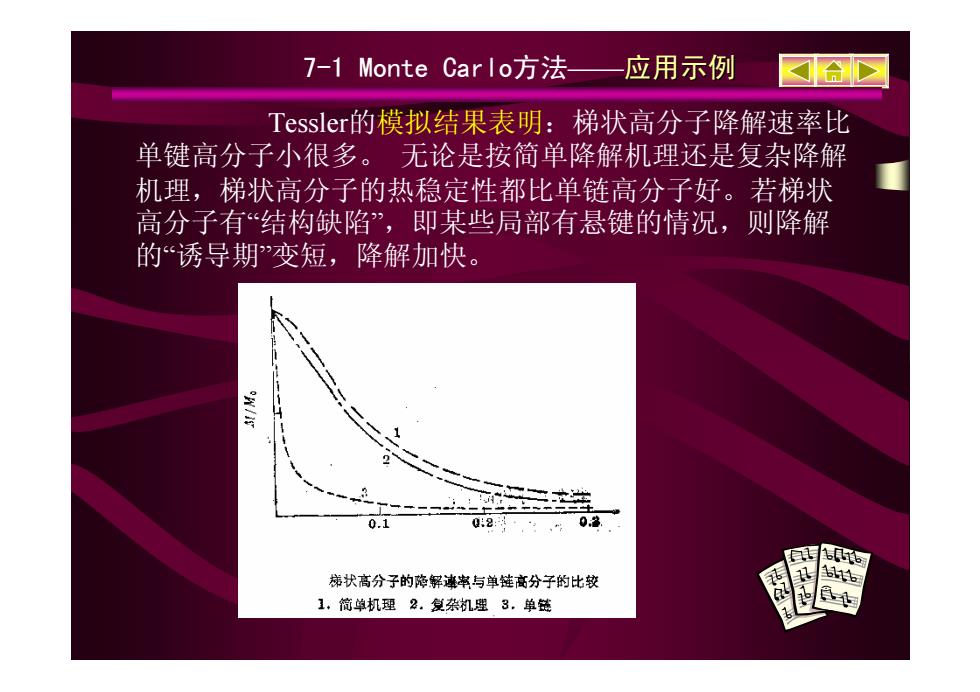
Tessler的模拟结果表明:梯状高分子降解速率比 单键高分子小很多。 无论是按简单降解机理还是复杂降解 机理,梯状高分子的热稳定性都比单链高分子好。若梯状 高分子有“结构缺陷”,即某些局部有悬键的情况,则降解 的“诱导期”变短,降解加快。 7-1 Monte Carlo方法——应用示例

合店 分子的计算机模拟 Molecular Modeling Atomic Simulation

合西 什么是分子 用计算机模拟化学体系 的微观结构和运动,并 计算机模拟? 用数值运算、统计求和 方法对系统的平衡热力 学、动力学、非平衡输 Wat飞 运等性质进行理论预测 分子模拟是化学CAD的 Molecular 重要工具之一 Modeling
What is Molecular Modeling ? • 用计算机模拟化学体系 的微观结构和运动,并 用数值运算、统计求和 方法对系统的平衡热力 学、动力学、非平衡输 运等性质进行理论预测 • 分子模拟是化学CAD 的 重要工具之一 什么是分子 计算机模拟 ? 什么是分子 计算机模拟 ?

合店 为何进行分子计算机模拟? ● 宏观化学现象是1024个分子(原孟)的集体行 为,固有统计属性 ·化学统计方学的局限性:通藏仅适用于 “理想体系 理想气体、完美品体、稀 溶液等 ·量子化学方法的局限性:对象为平衡态、 单分子或元个分子组成的本系;不适用于 动力学过程和有温度压力变化的体系
为何进行分子计算机模拟 为何进行分子计算机模拟 ? • 宏观化学现象是 ~1024个分子(原子)的集体行 为,固有统计属性 • 化学统计力学的局限性:通常仅适用于 “理想体系 ” ⎯ 理想气体、完美晶体、稀 溶液等 • 量子化学方法的局限性:对象为平衡态、 单分子或几个分子组成的体系;不适用于 动力学过程和有温度压力变化的体系

✉合 分子模拟将原子、分子按经典粒子处理, 可提供微观结构、运动过程以及它们与宏 观性质相关的数据和直观图像 结果精度取决于所采用的粒子间作用势的 合理、精确程度。又称为“计算机实验”, 是理论与真实实验之间的桥梁 两种主要的分子模拟方法: (1)分子动力学法(MD,Molecular Dynamics) 基于粒子运动的经典轨迹 (2)Monte Carloi法(MC)一基于统计力学
结果精度取决于所采用的粒子间作用势的 合理、精确程度。又称为 “计算机实验 ”, 是理论与真实实验之间的桥梁 分子模拟将原子、分子按经典粒子处理, 可提供微观结构、运动过程以及它们与宏 观性质相关的数据和直观图像 两种主要的分子模拟方法: ⑴分子动力学法 (MD, Molecular Dynamics) ⎯ 基于粒子运动的经典轨迹 ⑵ Monte Carlo 法 (MC) ⎯ 基于统计力学

合店 分子力学法 Molecular Mechanics Method 分子力学法(MM)用于预测大分子的儿何构 型,其势函数可用于分子动力学模拟(MD) 一、 原理 ● 原子视为经典粒子,原子间作用力用经验势 函数表示 ·体系的平衡几何结构由能量最低原理确定
一、原理 • 原子视为经典粒子,原子间作用力用经验势 函数表示 • 体系的平衡几何结构由能量最低原理确定 分子力学法(MM)用于预测大分子的几何构 型,其势函数可用于分子动力学模拟(MD)
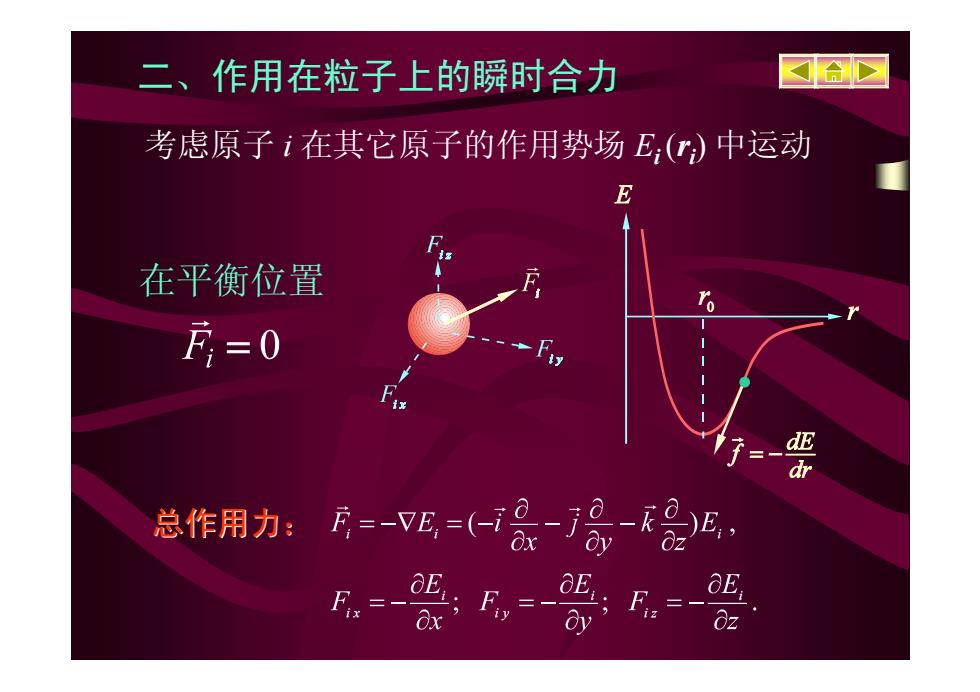
二、作用在粒子上的瞬时合力 合 考虑原子i在其它原子的作用势场E,(r)中运动 E 在平衡位置 万=0 ix d 总作用力:=-vE=(仁7品-了奇-是, 迟,器 号 E
二、作用在粒子上的瞬时合力 考虑原子 i 在其它原子的作用势场 Ei ( r i) 中运动 在平衡位置 总作用力: