
北京化工大学2011一一2012学年第二学期 《计算化学》期末考试试卷标准答案 第一部分笔试部分(共30分) 一.判断题,正确的在括号中划“√”,错误的划“×”(每题1分,共10分) 1.√2.×3.√4.×5.×6.×7.√8.×9.V10.V 二.填空题(每空1分,共20分) 1.∫(x)有明确表示式且容易计算:容易确定根的初值x0 2.差商 3.选主元、消元、回代 4.插值法:回归分析:函数:相关 5.最小二乘法 6.相关系数;1 7.复化求积;用插值程序求任意点的函数值;用Simpson2求积程序计算[a,b] 区间中离散点下的面积。 8.Euler法;Runge-Kutta法;化学动力学 9.反射、收缩、扩张 10.随机数:牛顿运动方程 第二部分上机题(共70分) A 1.计算原理(化学原理和计算方法)(15分)
1 北京化工大学 2011——2012 学年第二学期 《计算化学》期末考试试卷标准答案 第一部分 笔试部分(共 30 分) 一.判断题,正确的在括号中划“ √ ”,错误的划“ × ”(每题 1 分,共 10 分) 1.√ 2.× 3.√ 4.× 5.× 6.× 7.√ 8.× 9.√ 1 0.√ 二.填空题(每空 1 分,共 20 分) 1. f’(x)有明确表示式且容易计算;容易确定根的初值 x0 2. 差商 3. 选主元、消元、回代 4. 插值法;回归分析;函数;相关 5. 最小二乘法 6. 相关系数;1 7. 复化求积;用插值程序求任意点的函数值;用Simpson求积程序计算[a,b] 区间中离散点下的面积。 8. Euler 法;Runge-Kutta 法;化学动力学 9. 反射、收缩、扩张 10. 随机数;牛顿运动方程 第二部分 上机题(共 70 分) A 1.计算原理(化学原理和计算方法)(15 分)
根据Arrhenius公式 k=Ae-E./RT (1) (3分) (1)式两边取对数得 hkeh4是 (2) (3分) 令 y=nkx=7a=hAh=-是 (3分) 得 y=a+bx 根据k和T数据,采用一元线性回归方法,求出a,b:然后可确定指前因子 A和活化能Ea。根据相关系数判断数据的相关性。 (3分) A=exp(a,E。=-bR (3分) 2.程序框图(20分)》 [开始 输入:温度T(ID,速率常数K(I)(2分) N)(4分) 计算:Y(I)=LOG(K①) X⑩=1/T0⊥(6分) 调用一元线性回归子程序求解方程计算α,b(4分) 相关系数RR 计算定指前因子AA(I)=exp(a() 和活化能EA(I=b①)*R(4分) 输出:AA,EA,RR值(4分) 结束 3.源程序(20分) PROGRAM MAIN (15分)
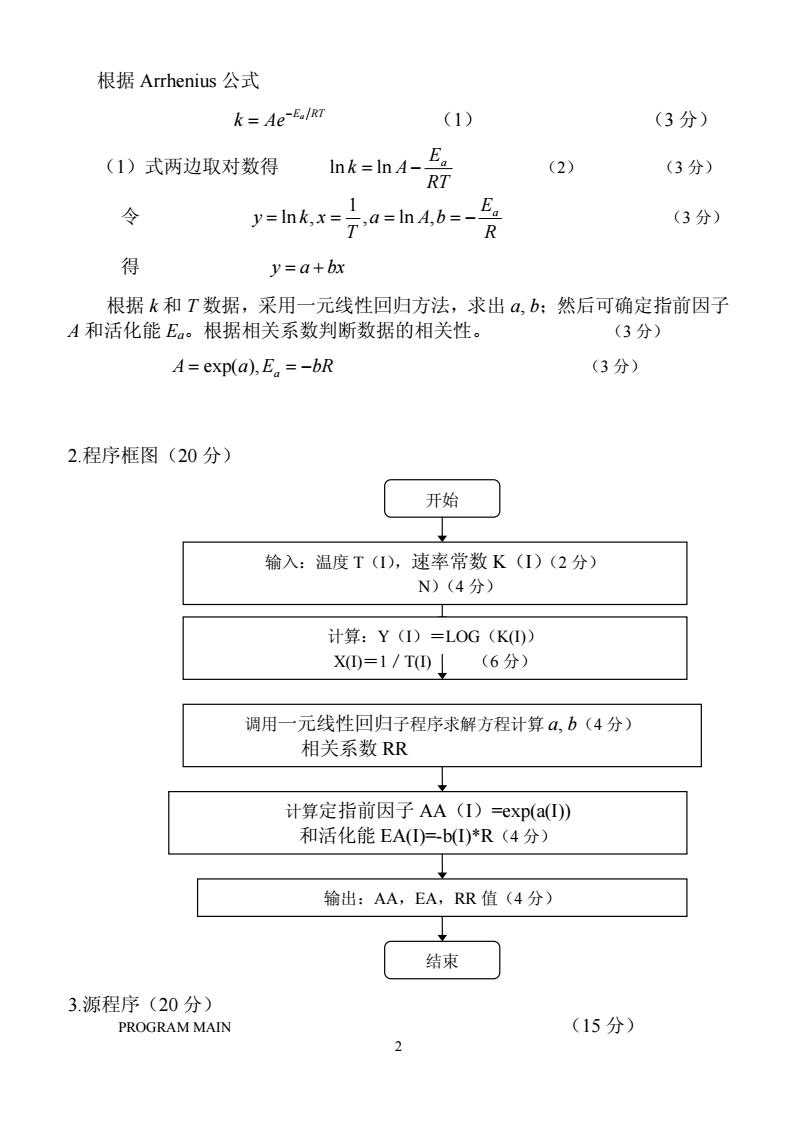
2 根据 Arrhenius 公式 Ea RT k Ae− = (1) (3 分) (1)式两边取对数得 RT E k A a ln = ln − (2) (3 分) 令 R E a A b T y k x a = = , = ln , = − 1 ln , (3 分) 得 y = a + bx 根据 k 和 T 数据,采用一元线性回归方法,求出 a, b;然后可确定指前因子 A 和活化能 Ea。根据相关系数判断数据的相关性。 (3 分) A = exp(a),Ea = −bR (3 分) 2.程序框图(20 分) 3.源程序(20 分) PROGRAM MAIN (15 分) 开始 计算:Y(I)=LOG(K(I)) X(I)=1/T(I) (6 分) 调用一元线性回归子程序求解方程计算 a, b(4 分) 相关系数 RR 输出:AA,EA,RR 值(4 分) 结束 计算定指前因子 AA(I)=exp(a(I)) 和活化能 EA(I)=-b(I)*R(4 分) 输入:温度 T(I),速率常数 K(I)(2 分) N)(4 分)

DIMENSION X(5).Y(5),T(5),K(5) DOUBLE PRECISION X,Y.A,B.R,K,T,AA,EA OPEN(6,FILE-2012TA.TXT,STATUS-UNKNOWN) N=5 DATA T/592.603.,627.,652656/ DATA K/522,755.,1700.,4020.,5030/ D0100=1,N X=/T④ Y(I)=LOG(K(D)) 100 CONTINUE CALL PK(N,X,Y,A,B,R) (5分) EA=-8.314*B AA=EXP(A) WRITE(6,11)A,B.R.EA,AA 11 FORMAT5X,'A=,D18.10/5X,'B=,D18.10,5X'R=,D18.10M& X,'EA/JMOL-I-,D18.10.5X:'A/cm3-mol-1-s-1=D18.10//) EN SUBROUTINE PK(N.X,Y,A,B,R) DOUBLE PRECISION X.YA.B.R DIMENSION X(N),Y(N) SX-0.0 SY=0.0 5XX0.0 SYY=0.0 SXY-0.0 D010I=1,N X1=X0 SX=SX+X SXX-SXX+X1*X SYY-SYY+Y1Y SXY=SXY+X1+Y 10 NTIN DX XS> YY-SYY-SY"SY/ DXY-SX B-DXY/DX R-DEB-SXYN XY RT(DXX*DYY) END 4.运行结果(15分) A 2914848931D+02 B=-1357367593D+05 R=-.9987366682D00 (5分) EA/JMOL-1= 1128515434D+06 (5分)》 A/cm3-mol-Is-1= :.4560663872D+13 (5分) 3
3 DIMENSION X(5),Y(5),T(5),K(5) DOUBLE PRECISION X,Y,A,B,R,K,T,AA,EA OPEN(6,FILE='2012TA.TXT', STATUS='UNKNOWN') N=5 DATA T/592.,603.,627.,652.,656./ DATA K/522.,755.,1700.,4020.,5030./ DO 100 I=1,N X(I)=1/T(I) Y(I)=LOG(K(I)) 100 CONTINUE CALL PK(N,X,Y,A,B,R) (5 分) EA=-8.314*B AA=EXP(A) WRITE(6,11)A,B,R,EA,AA 11 FORMAT(/5X,'A=',D18.10//5X,'B=',D18.10, 5X,'R=',D18.10// & 5X,'EA/JMOL-1=',D18.10,5X,'A/cm3·mol-1·s-1=',D18.10//) END SUBROUTINE PK(N,X,Y,A,B,R) DOUBLE PRECISION X,Y,A,B,R DIMENSION X(N),Y(N) SX=0.0 SY=0.0 SXX=0.0 SYY=0.0 SXY=0.0 DO 10 I=1,N X1=X(I) Y1=Y(I) SX=SX+X1 SY=SY+Y1 SXX=SXX+X1*X1 SYY=SYY+Y1*Y1 SXY=SXY+X1*Y1 10 CONTINUE DXX=SXX-SX*SX/N DYY=SYY-SY*SY/N DXY=SXY-SX*SY/N B=DXY/DXX A=(SY-B*SX)/N R=DXY/SQRT(DXX*DYY) RETURN END 4.运行结果(15 分) A= .2914848931D+02 B= -.1357367593D+05 R= -.9987366682D+00 (5 分) EA/JMOL-1= .1128515434D+06 (5 分) A/cm3·mol-1·s-1= .4560663872D+13 (5 分)

B 1.计算原理(化学原理和计算方法)(15分) 设平衡时C2H,生成物质的量为xmol 根据反应式 C2H2+H2=-=C2Ha 起始物质的量mol 1 1 0 平衡物质的量/mol 1-x1-x 反应达平衡时系统中总物质的量为:1-x+1-x+x=2-x 故平衡时系统中各物质的组成为: 1-x e:=2-x2 _1-x m:=2-x yCH.=2-x 式中:y为物质的量分数 (5分) 代入平衡关系式得: 「p 7- =1.000 (1) (1-x)1-x)(2-x)p° (1)式经整理后得 7-1 -1.000=0 (2) (1-x)1-x)L(2-x)p° 7 令:f(x)= (5分) (1-x1-x)(2-x)p° -1.000 调用二分法求解方程f(x)=0 取值范围:0.0~1.0 (5分) 2.程序框图(20分) 开始
4 B 1. 计算原理(化学原理和计算方法)(15 分) 设平衡时 C2H4 生成物质的量为 x mol 根据反应式 C2H2 + H2 === C2H4 起始物质的量/mol 1 1 0 平衡物质的量/mol 1- x 1- x x 反应达平衡时系统中总物质的量为: 1− x +1− x + x = 2 − x 故平衡时系统中各物质的组成为: , 2 2 1 , 2 1 2 4 2 2 2 C H C H H x x y x x y x x y − = − − = − − = 式中:y 为物质的量分数。 (5 分) 代入平衡关系式得: 1.000 (1 )(1 ) (2 ) ( ) 1 = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − − − = ∑ = − ∑ θ ν θ θ x p p x x x n p p K K B B n (1) (1) 式经整理后得 1.000 0 (1 )(1 ) (2 ) 1 − = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − − − − θ x p p x x x (2) 令: 1.000 (1 )(1 ) (2 ) ( ) 1 − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − − − = − θ x p p x x x f x (5 分) 调用二分法求解方程 f (x) = 0 取值范围 :0.0~1.0 (5 分) 2. 程序框图(20 分) 开始

输入:温度T,压力P,标准平衡常数K,EPS(4分) 输入二分区间A=0.0,B=1.0(4分) 调用二分法子程序求解方程f(x)=0(4分》 (其中调用自编子程序计算f(x)值)得C2H4的生成物质的量x 计算平衡时各组分的物质的量分数YC1,YH1,YC2(4分) 输出:T,P,x,YC1,YH1,YC2值(4分) 结束 3.源程序(20分) PROGRAM MAIN (15分) REAL TP.K,EPS,YCI,YHI,YC2,X EXTERNAL F COMMON】 OPEN(6.FILI 2012TESTB.TXT.STATUS-UNKNOWN) DATA T/1393.2 DATA EPS/IE-6/ 1.013E06 K=1.000 10 EPS=1.0E-6 CALLHALF(A,B.EPS.F.X) 2-X /2- WRITE(6 11)T.PX.YC1.YH1.YC2 END FUNCTION F(X) (5分 REAL X.P
5 3. 源程序(20 分) PROGRAM MAIN (15 分) REAL T,P,K,EPS,YC1,YH1,YC2,X EXTERNAL F COMMON P OPEN(6,FILE='2012TESTB.TXT',STATUS='UNKNOWN') DATA T/1393.2/ DATA EPS/1E-6/ P=1.013E06 K=1.000 A=0.0 B=1.0 EPS=1.0E-6 CALL HALF(A,B,EPS,F,X) YC1=(1-X)/(2-X) YH1=(1-X)/(2-X) YC2=X/(2-X) WRITE(6,11)T,P,X,YC1,YH1,YC2 11 FORMAT(/5X,'T=',F10.4,'K'/5X,'P=',G12.4,'Pa'/& /5X,'X=',F6.4//'RESULT:'/5X,'y(C2H2)=',F6.4 & /5X,'y(H2)=',F6.4 /5X,'y(C2H4)=',F6.4) END FUNCTION F(X) (5 分) REAL X,P 输入:温度 T,压力 P,标准平衡常数 K,EPS(4 分) 调用二分法子程序求解方程 f (x) = 0(4 分) (其中调用自编子程序计算 f (x) 值)得 C2H4 的生成物质的量 x 输出:T,P,x,YC1,YH1,YC2 值(4 分) 结束 输入二分区间 A=0.0,B=1.0(4 分) 计算平衡时各组分的物质的量分数 YC1,YH1,YC2(4 分)
COMMON P X1-X1-X)*(2-X)*1.013E5/Py-1.000 SUBROUTINE HALF(A.B.EPS.F.X) REALA.B.EPS Y0-F(A) AI=A BI=B K=0 10 X=(A1+B1)*0.5 Y=F(X YO GTOOAI=X IFCY*YOLE00)BI=X IF(ABS(BI-AIVX.GT.EPS)GOTO 10 IF(K.GT.50)THEN END IF X=(A1+B1)*0.5 30 RETURN END 4.运行结果(15分) 19 (3分) RESULT: y(C2H2 2317 (4 y(H2) 23 分) y(C2H4)=.5367 (4分 C 一反应按以下机理进行: →A3 +A4 己知k1=3.28×103s,k1=1.64×103s,2=6.56×103s,k3=3.28×103s, 设反应开始时只有A,A2,初始浓度分别为2.00 mol-dm,1.00 mol-dm,试计 6
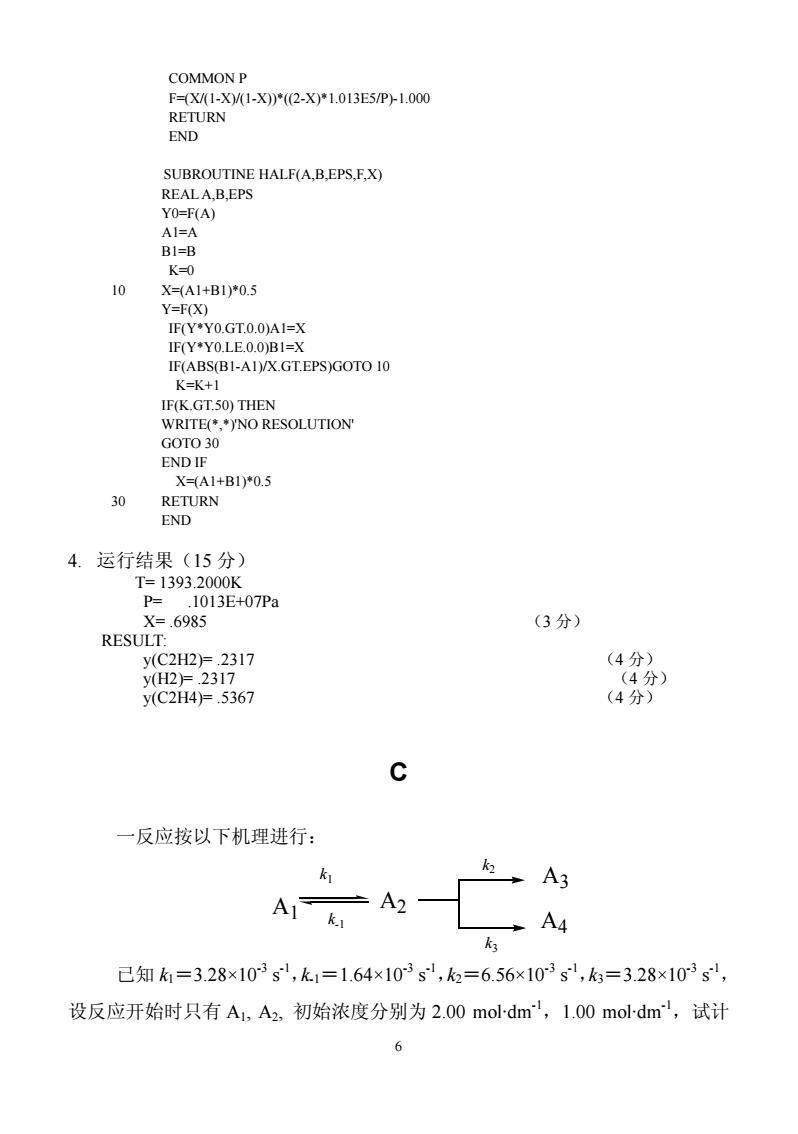
6 COMMON P F=(X/(1-X)/(1-X))*((2-X)*1.013E5/P)-1.000 RETURN END SUBROUTINE HALF(A,B,EPS,F,X) REAL A,B,EPS Y0=F(A) A1=A B1=B K=0 10 X=(A1+B1)*0.5 Y=F(X) IF(Y*Y0.GT.0.0)A1=X IF(Y*Y0.LE.0.0)B1=X IF(ABS(B1-A1)/X.GT.EPS)GOTO 10 K=K+1 IF(K.GT.50) THEN WRITE(*,*)'NO RESOLUTION' GOTO 30 END IF X=(A1+B1)*0.5 30 RETURN END 4. 运行结果(15 分) T= 1393.2000K P= .1013E+07Pa X= .6985 (3 分) RESULT: y(C2H2)= .2317 (4 分) y(H2)= .2317 (4 分) y(C2H4)= .5367 (4 分) C 一反应按以下机理进行: A1 k1 k-1 A2 k2 k3 A4 A3 已知 k1=3.28×10-3 s-1,k-1=1.64×10-3 s-1,k2=6.56×10-3 s-1,k3=3.28×10-3 s-1, 设反应开始时只有 A1, A2, 初始浓度分别为 2.00 mol·dm-1,1.00 mol·dm-1,试计
算反应经过100s后,A1,A2的转化率。 1.计算原理(化学原理和计算方法)(15分) 机理: A3 、A4 其动力学方程式为一个常微分方程组: d[A ]=-k[A.]+k[A:] dt d[A:]-[A.]-k[A:]-kIA:]-k[A:] d (8分) d[A]=ka[A:] dt d[A]=k[A:] d 利用Runge-Kutta法解此方程组,可得反应进行前100s时每隔20s[A],A],[A], [A4 (3分) 设反应经过100s后A,A2的转化率分别为x1,x2 则 x=[41-100./八410 (4分) X=[42 1-100,/[A2 l-os 2.程序框图(20分) 开始 输入:A,[A[A,[A4初值 时间间隔H,计算精度EPS (5分) 计算:积分步长H0(2分) 调用变步长Runge-Kutta法子程序解动力学方程组计算时刻t的 [A,[A],[A,[A4值 其中调用计算动力学方程组的子程序计算DY值)(5分)
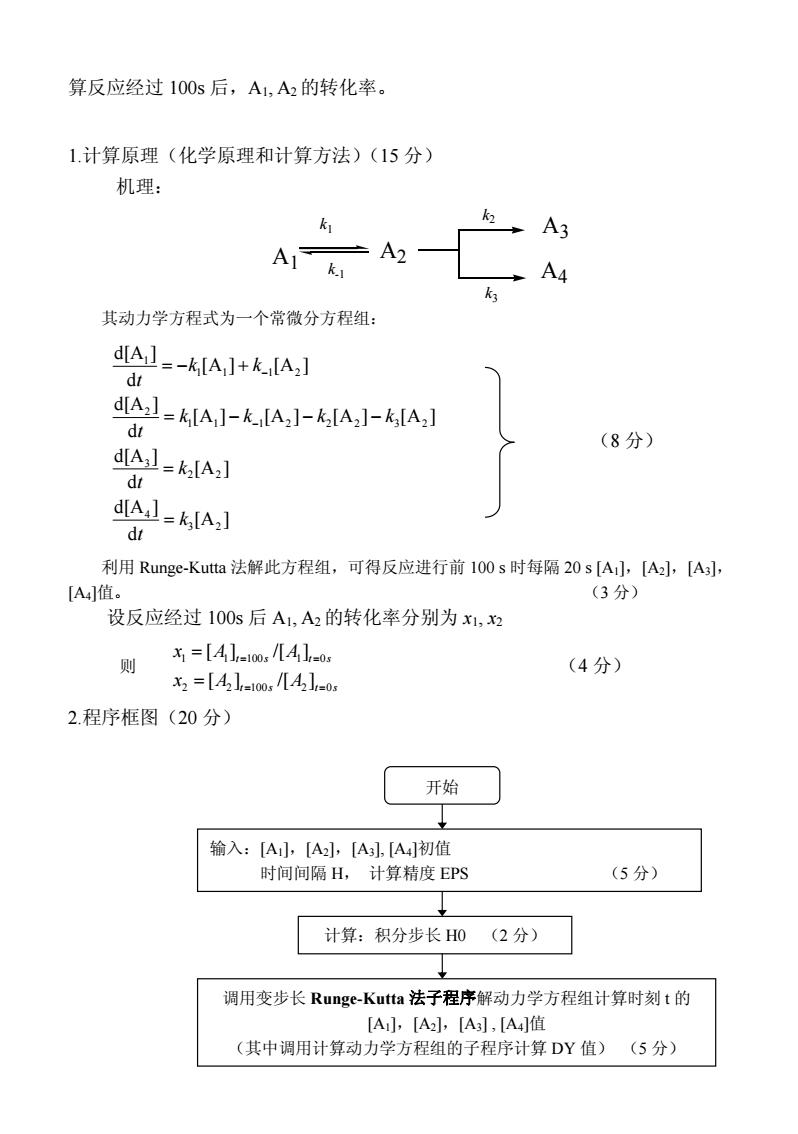
7 算反应经过 100s 后,A1, A2 的转化率。 1.计算原理(化学原理和计算方法)(15 分) 机理: A1 k1 k-1 A2 k2 k3 A4 A3 其动力学方程式为一个常微分方程组: [A ] d d[A ] [A ] d d[A ] [A ] [A ] [A ] [A ] d d[A ] [A ] [A ] d d[A ] 3 2 4 2 2 3 1 1 1 2 2 2 3 2 2 1 1 1 2 1 k t k t k k k k t k k t = = = − − − = − + − − (8 分) 利用 Runge-Kutta 法解此方程组,可得反应进行前 100 s 时每隔 20 s [A1],[A2],[A3], [A4]值。 (3 分) 设反应经过 100s 后 A1, A2 的转化率分别为 x1, x2 则 t s t s t s t s x A A x A A 2 2 100 2 0 1 1 100 1 0 [ ] /[ ] [ ] /[ ] = = = = = = (4 分) 2.程序框图(20 分) 输入:[A1],[A2],[A3], [A4]初值 时间间隔 H, 计算精度 EPS (5 分) 计算:积分步长 H0 (2 分) 调用变步长 Runge-Kutta 法子程序解动力学方程组计算时刻 t 的 [A1],[A2],[A3] , [A4]值 (其中调用计算动力学方程组的子程序计算 DY 值) (5 分) 开始

列表输出:反应进行前100s中每隔20s时所对应的 [A,[A,[A[A值 (3分) 输出:反应经过100s后A,A2的转化率分别为x,2 (5分) x=[4l=oo.儿4l-s 为3=[4l=m.爪4,]20s 结束 3.源程序(20分) PROGRAM MAIN (15分) IMPLICIT REAL *8(A-H.O-Z) DIMENSION YO(10).Y1(10).Y2(10) OPEN(6,FILE-2012TESTC.TXT,STATUS-UNKNOWN) DATA Y02.0,1.0.8*0.0/ N=4 T0=0.0 T1=100.0 H0=20.0 EPS=1.0E-6 H=HO WRITE(6.11)N.TO,TI.HO,EPS WRITE(6,22)T0,H,Y00,=1,N) M=IDINT((TI-TOYHO) D08010=1,M K=1 CALLRK4(TO.Y0.Y1.HO.N,K) D030KK=1,100 K-K+K H=HO/K CALLRK4(TO.Y0.Y2.,H.N.K) ES=0.0 D010J=1,N 10 ES=ES+ABS((Y2(J)-Y1()Y2(J)) IF(ES.LT.EPS)GOTO 50 D020J=1N Y1)=Y20 30 CONTINUE WRITE(6,33) STOP T0=T0+H0 DO 60 J=I.N 60 YO(JY2(J)
8 3.源程序(20 分) PROGRAM MAIN (15 分) IMPLICIT REAL *8(A-H,O-Z) DIMENSION Y0(10),Y1(10),Y2(10) OPEN(6,FILE='2012TESTC.TXT',STATUS='UNKNOWN') DATA Y0/2.0,1.0,8*0.0/ N=4 T0=0.0 T1=100.0 H0=20.0 EPS=1.0E-6 H=H0 WRITE(6,11)N,T0,T1,H0,EPS WRITE(6,22)T0,H,(Y0(I),I=1,N) M=IDINT((T1-T0)/H0) DO 80 I0=1,M K=1 CALL RK4(T0,Y0,Y1,H0,N,K) DO 30 KK=1,100 K=K+K H=H0/K CALL RK4(T0,Y0,Y2,H,N,K) ES=0.0 DO 10 J=1,N 10 ES=ES+ABS((Y2(J)-Y1(J))/Y2(J)) IF(ES.LT.EPS)GOTO 50 DO 20 J=1,N 20 Y1(J)=Y2(J) 30 CONTINUE WRITE(6,33) STOP 50 T0=T0+H0 DO 60 J=1,N 60 Y0(J)=Y2(J) 列表输出:反应进行前 100s 中每隔 20s 时所对应的 [A1],[A2],[A3] [A4]值 (3 分) 结束 输出:反应经过 100s 后 A1, A2 的转化率分别为 x1, x2 (5 分) t s t s A t s A t s x A A x 1 1 100 1 0 2 2 100 2 0 [ ] /[ ] [ ] /[ ] = = = = = =

WRITE(6,22)T0,H,(Y20,I=1,N) 80 CONTINUE XA1=1-Y2(1)W2.0 XA2=1-Y2(2V1.0 WRITE(6,44) WRITE(6.40)XAL.XA2 11 F0 RMAT(/1XN=,I2,2XT0=,F6.1,2X,T1=,F8.1,2X,& H0=,G8.3,1XEPS=,G10.3/20X,Y①,=1,2,3,4,N1& 1X,96(1H-Y5X.'t/min'.3X.'H/min'.6X.'[A1VmolL-I'. 6X.[A2]/molL-1',6X,'[A3]/molL-1'& /1X,96(1H-) FORMAT(IX,2F8.2.2X,3G15.6) 33 FORMAT(/IX,'FAILED TO FIND STABLE SOLUTION IN MAX IT/) FORMAT(IX.'X[AIF,F8.4.5X,'X[A2.F8.4) 44 FORMAT(IX96(1H-)》 END SUBROUTINE F(Y,DY) (5分) IMPLICIT REAL *8(A-H,O-Z) REAL *8 KI,K11,K2,K3 DIMENSION Y(10),DY(10) DATA K13.28E-3/,K11/1.64E-3,K2/6.56E-3/,K3/3.28E-3/ DYI户-KIY(1+KIIY(2) DY(2=K1*Y(I)-K11*Y(2)K2*Y(2)K3*Y(2) DY(3-K2*Y(2) DY(4=K3*Y(2) RETURN END DIMENSION Y2(20),DY(20),RK(20) X-X0 D05=l, 5 =. -DY(I) 10 D)+0.5*H*DY(I) 20 DY 30 Y①+H*DY CALL F(Y2.DY)
9 WRITE(6,22)T0,H,(Y2(I),I=1,N) 80 CONTINUE XA1=1-Y2(1)/2.0 XA2=1-Y2(2)/1.0 WRITE(6,44) WRITE(6,40) XA1,XA2 11 FORMAT(/1X,'N=',I2,2X,'T0=',F6.1,2X,'T1=',F8.1,2X, & 'H0=',G8.3,1X,'EPS=',G10.3//20X,'Y(I),I=1,2,3,4,...,N'//& 1X,96(1H-)/5X,'t/min',3X,'H/min',6X,'[A1]/molL-1', & 6X,'[A2]/molL-1',6X,'[A3]/molL-1'& /1X,96(1H-)) 22 FORMAT(1X,2F8.2,2X,3G15.6) 33 FORMAT(/1X,'FAILED TO FIND STABLE SOLUTION IN MAX IT'/) 40 FORMAT(1X,'X[A1]=',F8.4,5X,'X[A2]=',F8.4) 44 FORMAT(1X,96(1H-)) END SUBROUTINE F(Y,DY) (5 分) IMPLICIT REAL *8(A-H,O-Z) REAL *8 K1,K11,K2,K3 DIMENSION Y(10),DY(10) DATA K1/3.28E-3/,K11/1.64E-3/,K2/6.56E-3/,K3/3.28E-3/ DY(1)=-K1*Y(1)+K11*Y(2) DY(2)=K1*Y(1)-K11*Y(2)-K2*Y(2)-K3*Y(2) DY(3)=K2*Y(2) DY(4)=K3*Y(2) RETURN END SUBROUTINE RK4(X0,Y0,Y,H,N,M) IMPLICIT REAL *8(A-H,O-Z) DIMENSION Y0(N),Y(N) DIMENSION Y2(20),DY(20),RK(20) X=X0 DO 5 I=1,N 5 Y(I)=Y0(I) DO 50 L=1,M CALL F(Y,DY) DO 10 I=1,N RK(I)=DY(I) 10 Y2(I)=Y(I)+0.5*H*DY(I) CALL F(Y2,DY) DO 20 I=1,N RK(I)=RK(I)+2*DY(I) 20 Y2(I)=Y(I)+0.5*H*DY(I) CALL F(Y2,DY) DO 30 I=1,N RK(I)=RK(I)+2*DY(I) 30 Y2(I)=Y(I)+H*DY(I) CALL F(Y2,DY)

Dm思y ETURN EN 4.运行结果(15分) N=4T0= .0T1=100.0H0=20.0 EPS=.100E-05 Y①,=1,23,4N t/min H/min [AI]/molL-1 [A2]/molL-1 [A3YmolL-1 [A4]/molL-1 (5分) .0020.00 2.00000 1.00000 00000d 000000 20.00 5.00 1.90326 .909119 .125080 .625398E-01 40.00 5.00 1.81000 831317 239124 .119562 60.00 5.0 1.72036 764119 34368 ,17184 80.00 5.0 1.63443 .705565 .44000 .220003 100.00 5.00 1.55221 654100 .529130 264565 XA1]F2239 X[A2]= .3459 (10分) D 1.计算原理(化学原理和计算方法)(15分) 乙炔的摩尔热容Cp.m与温度T的经验关联式为 Cpm=a+bT+cT2 (1) 正规方程组 T105.21=8a+28b+140c 402.29=28a+140b+78c (2) C2070.29=140a+784b+467c 采用高斯消去法解方程组(2),可得到a,b,c的值。然后将a,b,c的值代 入(1),可得乙炔的摩尔热容与温度的经验关联式的具体形式。 2.程序框图(20分) 开始
10 DO 40 I=1,N RK(I)=RK(I)+DY(I) 40 Y(I)=Y(I)+RK(I)*H/6 50 CONTINUE RETURN END 4.运行结果(15 分) N= 4 T0= .0 T1= 100.0 H0=20.0 EPS= .100E-05 Y(I),I=1,2,3,4,...,N ----------------------------------------------------------------------------------------------------------------------- t/min H/min [A1]/molL-1 [A2]/molL-1 [A3]/molL-1 [A4]/molL-1 (5 分) ----------------------------------------------------------------------------------------------------------------------- .00 20.00 2.00000 1.00000 .000000 .000000 20.00 5.00 1.90326 .909119 .125080 .625398E-01 40.00 5.00 1.81000 .831317 .239124 .119562 60.00 5.00 1.72036 .764119 .343680 .171840 80.00 5.00 1.63443 .705565 .440006 .220003 100.00 5.00 1.55221 .654100 .529130 .264565 ---------------------------------------------------------------------------------------------------------------------- X[A1]= .2239 X[A2]= .3459 (10 分) D 1.计算原理(化学原理和计算方法)(15 分) 乙炔的摩尔热容 Cp,m与温度 T 的经验关联式为 2 ,m Cp = a + bT + cT (1) 正规方程组 a b c a b c a b c 2070.29 140 784 467 402.29 28 140 78 105.21 8 28 140 = + + = + + = + + (2) 采用高斯消去法解方程组(2),可得到 a,b, c 的值。然后将 a,b, c 的值代 入(1),可得乙炔的摩尔热容与温度的经验关联式的具体形式。 2.程序框图(20 分) 开始