
北京化工大学2002-2003学年第一学期 《计算化学》期末试卷答案(上机部分) 注:上机考试总分60分。 1.计算原理(化学原理和计算方法)(12分) 根据热力学知识,有 K 由上式得:KR=Kexp(S) 此题中,已知热烙与温度的关系:△H~T 可推导出识T关系,可根据离散点求积的方法即:用S1即sOn求积方法 RT2 (其中调用Lagrange插值法子程序计算任意点的函数值)计算S,然后通过S 求出773K下的平衡常数。 2.程序框图(18分) 开始 输入:热焓与温度△H~T的实验数据 X①.Y① XⅪ=X0,Y=YXI*XⅫ)=l,N 输入:积分上、下限T2,T1及KP1 两次调用Simpson积分法子程序计算面积S (其中调用Lagrange插值法子程序计算任意点的函数值) 计算KP2=KPI*EXP(S/R) 输出:KP2
北京化工大学 2002-2003 学年第一学期 《计算化学》期末试卷答案(上机部分) 注:上机考试总分 60 分。 A 1.计算原理(化学原理和计算方法)(12 分) 根据热力学知识,有 ∫ = Δ = 2 1 1 2 2 ln T T p p dT S RT H K K 由上式得: exp( ) 2 1 K p = K p ⋅ S 此题中,已知热焓与温度的关系:ΔH ~ T 可推导出 T RT H ~ 2 Δ 关系,可根据离散点求积的方法即:用 Simpson 求积方法 (其中调用 Lagrange 插值法子程序计算任意点的函数值)计算 S,然后通过 S 求出 773K 下的平衡常数。 2.程序框图(18 分) 开始 输入:热焓与温度 ΔH ~ T 的实验数据 X(I),Y(I) (I=1,N) 输入:积分上、下限 T2,T1 及 KP1 两次调用 Simpson 积分法子程序计算面积 S (其中调用 Lagrange 插值法子程序计算任意点的函数值) 计算 KP2=KP1*EXP(S/R) 输出:KP2 结束 XI=X(I),Y(I)=Y(I)/(XI*XI) (I=1,N)

3.源程序(18分) PROGRAM MAIN DOUBLE PRECISION EPS,A,B.X,Y,S,KP1,KP2 DIMENSION X(7Y(7) N=7 EPS=1.0E-5 OPEN(6,FILE=TESTA.Txt,STATUS-UNKNOWN) DATA X/623.0,648.0,673.0,698.0,723.0,748.0,773.0/ DATA Y1-50.7898,-5L.1390,-51.4738.-51.7943,-52.1006,& .52.3929-526715/ A-623 B=773 KP1-2644 D010I=1,N XI=XO 10 Y=YXI*XⅫ CALLSIMP(N.A.B.X.Y.EPS.S) R=8.314D-03 P21=DEXP(S/R) KP2=KP1*P21 WRITE(6.20)A.B.S WRITE(6.30)B.KPz F0RMAT(1X,'S,F6.2,K->',F6.2,K=,G12.6 30 FORMAT(1X.'Kp2(.F7.2.'KG12.6.'Pa-1) END SUBROUTINESIMP(M,A,B.X,Y.EPS.S2) DOUBLEPRECISIONA.B.X.Y.EPS.S2.FA.FB.X0.Y0 DIMENSION X(M).Y(MY H=B-A N=I CALLLGRG2CX YMA FAY CALLLGRG2(X.Y.M.B.FB) T1=0.5*H*(FA+FB) 10 S=0 D020K=1N X0=A+K-0.5)*H CALLLGRG2(X.Y.M.X0.Y0) 20 S=S+Y0 T2-0.5*(T1+H*S) S2=T2+T2-T1)M3.0
3.源程序(18 分) PROGRAM MAIN DOUBLE PRECISION EPS,A,B,X,Y,S,KP1,KP2 DIMENSION X(7),Y(7) N=7 EPS=1.0E-5 OPEN(6,FILE='TESTA.Txt',STATUS='UNKNOWN') DATA X/623.0,648.0,673.0,698.0,723.0,748.0,773.0/ DATA Y/-50.7898,-51.1390,-51.4738,-51.7943,-52.1006, & -52.3929,-52.6715/ A=623 B=773 KP1=2644 DO 10 I=1,N XI=X(I) 10 Y(I)=Y(I)/(XI*XI) CALL SIMP(N,A,B,X,Y,EPS,S) R=8.314D-03 P21=DEXP(S/R) KP2=KP1*P21 WRITE(6,20) A,B,S WRITE(6,30) B,KP2 20 FORMAT(1X,'S(',F6.2,'K-->',F6.2,'K)=',G12.6) 30 FORMAT(1X,'Kp2(',F7.2,'K)=',G12.6,'Pa-1') END SUBROUTINE SIMP(M,A,B,X,Y,EPS,S2) DOUBLE PRECISION A,B,X,Y,EPS,S2,FA,FB,X0,Y0 DIMENSION X(M),Y(M) H=B-A N=1 CALL LGRG2(X,Y,M,A,FA) CALL LGRG2(X,Y,M,B,FB) T1=0.5*H*(FA+FB) 10 S=0 DO 20 K=1,N X0=A+(K-0.5)*H CALL LGRG2(X,Y,M,X0,Y0) 20 S=S+Y0 T2=0.5*(T1+H*S) S2=T2+(T2-T1)/3.0

IFON.EO.DGOTO 40 30 D=ABS(S2-S1) IF(ABS(S2).GT.1.0)THEN D=ABS((S2-S1)S2) END IF IF(D.LT.EPS)GOTO 50 40 n=nin H=05*H T172 s1=S2 G0T010 50 Return END SUBROUTINE LGRG2(X.Y.N.T.Z) DIMENSION X(N)Y(N) DOUBLE PRECISION X.Y.T.Z.S 7=00 IF(N.LE.O)RETURN IF(N.EQ.1)THEN Z=Y1) RETURN END IF IF(N.EQ.2)THEN ZY1)*(TX2Y(2)*(T-X1)MX1)X2) RETURN END IF IF(T.LE.X(2))THEN K=1 M=3 ELSE IF(T.GE.X(N-1)YTHEN K=N-2 M=N ELSE 10 IF(IABS(K-M).NE.1)THEN L-K+M0/2 IF(TLTXOLDTHEN M-I ELSE K=L ENDIF G0T010
IF(N.EQ.1)GOTO 40 30 D=ABS(S2-S1) IF(ABS(S2).GT.1.0)THEN D=ABS((S2-S1)/S2) END IF IF(D.LT.EPS)GOTO 50 40 N=N+N H=0.5*H T1=T2 S1=S2 GOTO 10 50 RETURN END SUBROUTINE LGRG2(X,Y,N,T,Z) DIMENSION X(N),Y(N) DOUBLE PRECISION X,Y,T,Z,S Z=0.0 IF(N.LE.0)RETURN IF(N.EQ.1)THEN Z=Y(1) RETURN END IF IF(N.EQ.2)THEN Z=(Y(1)*(T-X(2))-Y(2)*(T-X(1)))/(X(1)-X(2)) RETURN END IF IF(T.LE.X(2))THEN K=1 M=3 ELSE IF(T.GE.X(N-1))THEN K=N-2 M=N ELSE K=1 M=N 10 IF(IABS(K-M).NE.1)THEN L=(K+M)/2 IF(T.LT.X(L))THEN M=L ELSE K=L ENDIF GOTO 10

END IF IF(ABS(T-X(K).LT.ABS(T-X(M)))THEN M=M+1 ENDIF END IF Z=00 DO30I-K.M S=1.0 DO20J-K.M IF(J.NE.I)THEN S=S*(T-X(J)Y(X(I)-X(J) END IE 20 CONTINUE Z=Z+S*Y(I) 30 CONTINUE RETurn END 4.运行结果。(12分) S623.00K>773.00K)=.161056E-01 Kp2(773.00K)=381.032 Pa-I B 1.计算原理(化学原理和计算方法)(12分) 化学反应速率方程: v=-de=ke dt 式中,y为化学反应速率,c为反应物浓度,1为时间,n为反应级数, k为反应速率常数,dcdu为反应物浓府随时间的变化率。 对气相反应 =p1 d 式中,p为反应物分压。 丙边取对数:hv=-当=h+nlhp 将实验所测得不同时间1的反应物分压P数据通过插值和差分法求出反应速率V。计算 nv和p后,用线性回归子程序计算反应级数n和反应速率常数k 2.程序框图(18分) 开始
END IF IF(ABS(T-X(K)).LT.ABS(T-X(M))) THEN K=K-1 ELSE M=M+1 END IF END IF Z=0.0 DO 30 I=K,M S=1.0 DO 20 J=K,M IF(J.NE.I)THEN S=S*(T-X(J))/(X(I)-X(J)) END IF 20 CONTINUE Z=Z+S*Y(I) 30 CONTINUE RETURN END 4.运行结果。(12 分) S(623.00K-->773.00K)=-.161056E-01 Kp2( 773.00K)= 381.032 Pa-1 B 1.计算原理(化学原理和计算方法)(12 分) 化学反应速率方程: n kc t c = − = d d ν 上式中,ν 为化学反应速率,c 为反应物浓度,t 为时间, n 为反应级数, k 为反应速率常数,dc/dt 为反应物浓度随时间的变化率。 对气相反应 n kp t p = − = d d ν 式中, p 为反应物分压。 上两边取对数: k n p t p ) ln ln d d lnν = ln(− = + 将实验所测得不同时间 t 的反应物分压 p 数据通过插值和差分法求出反应速率ν 。计算 lnν 和 lnp 后,用线性回归子程序计算反应级数 n 和反应速率常数 k。 2.程序框图(18 分) 开始
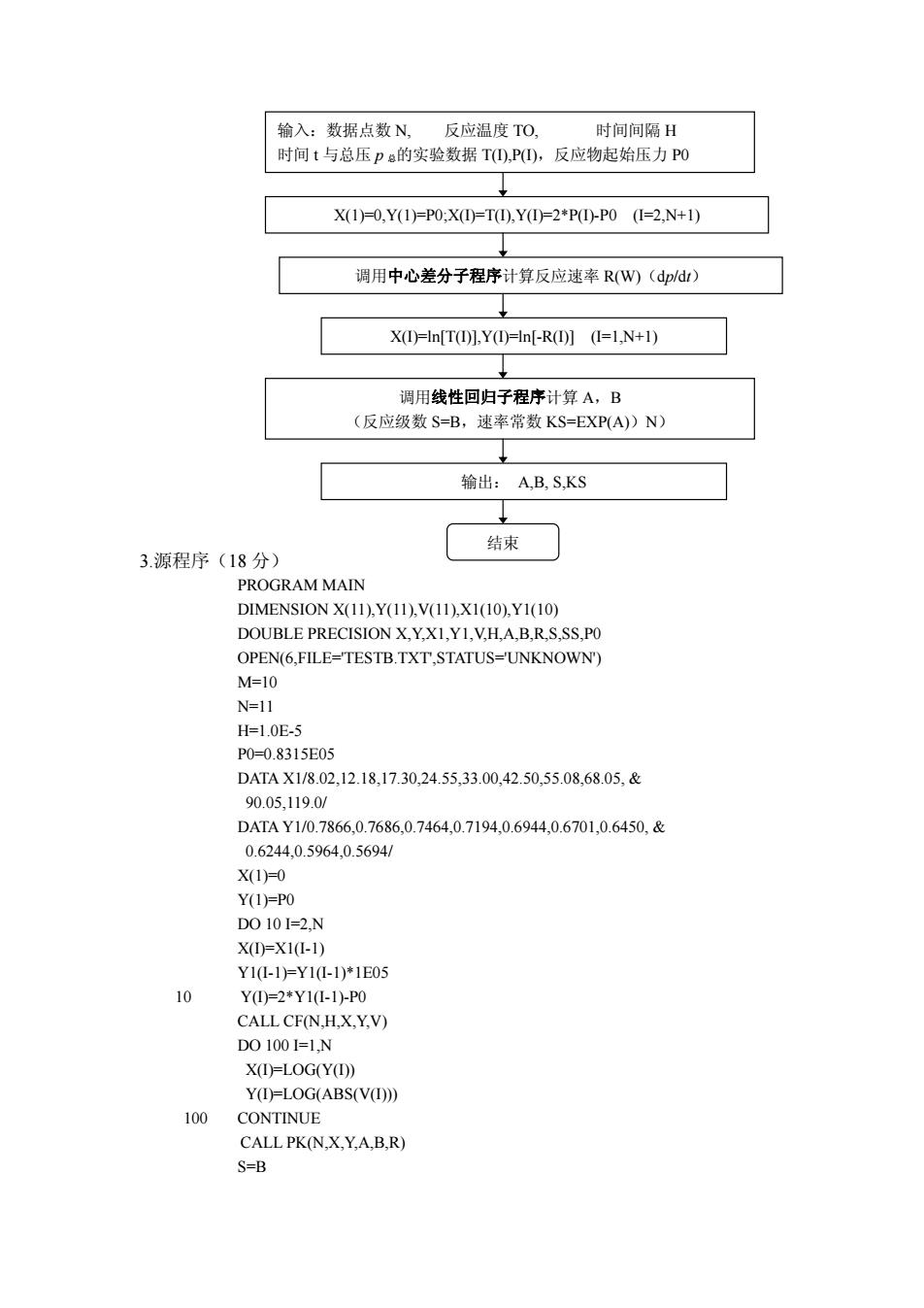
输入:数据点数N, 反应温度TO, 时间间隔H 时间t与总压P的实验数据T),P),反应物起始压力PO X1)0,Y1)=P0,X=T,Y0F2*P)-P0(I=2,N+1) 调用中心差分子程序计算反应速率R(W)(dp/dr) X(I)=ln[T(D)].Y(D)=ln[-R(D)](I=1.N+I) 调用线性回归子程序计算A,B (反应级数S=B,速率常数KS=EXP(A)N) 输出:A,BS,KS 3.源程序(18分) 结束 PROGRAM MAIN DIMENSION X(11).Y(11).V(11),XI(10),YI(10) DOUBLE PRECISIONX,Y.X1.Y1,V.H.A.B,R.S.SS.P0 OPEN(6,FILE-TESTB.TXT.STATUS-UNKNOWN) M=10 N-lI H=1.0E-5 P0=0.8315E05 DATA X1/8.02,12.18,17.30.24.55,33.00,42.50,55.08,68.05,& 90.05.1190/ DATAY1/0.78660.76860.7464,0.71940.6944,0.6701,0.6450,& 0.6244,0.5964,0.569 X(1=0 Y(1=P0 D0101=2N X0=X1-1 Y1-1)=Y1(-1)*1E05 10 YI=2*Y1L-1)-P CALLCF(N,H.X,Y.V) D01001=1N X(D-LOG(Y(D) Y(I)-LOG(ABS(V 100 CONTINUE CALLPK(N.X.Y.A.B.R) S=B
3.源程序(18 分) PROGRAM MAIN DIMENSION X(11),Y(11),V(11),X1(10),Y1(10) DOUBLE PRECISION X,Y,X1,Y1,V,H,A,B,R,S,SS,P0 OPEN(6,FILE='TESTB.TXT',STATUS='UNKNOWN') M=10 N=11 H=1.0E-5 P0=0.8315E05 DATA X1/8.02,12.18,17.30,24.55,33.00,42.50,55.08,68.05, & 90.05,119.0/ DATA Y1/0.7866,0.7686,0.7464,0.7194,0.6944,0.6701,0.6450, & 0.6244,0.5964,0.5694/ X(1)=0 Y(1)=P0 DO 10 I=2,N X(I)=X1(I-1) Y1(I-1)=Y1(I-1)*1E05 10 Y(I)=2*Y1(I-1)-P0 CALL CF(N,H,X,Y,V) DO 100 I=1,N X(I)=LOG(Y(I)) Y(I)=LOG(ABS(V(I))) 100 CONTINUE CALL PK(N,X,Y,A,B,R) S=B 输入:数据点数 N, 反应温度 TO, 时间间隔 H 时间 t 与总压 p 总的实验数据 T(I),P(I),反应物起始压力 P0(I=1, X(1)=0,Y(1)=P0;X(I)=T(I),Y(I)=2*P(I)-P0 (I=2,N+1) 调用中心差分子程序计算反应速率 R(W)(dp/dt) X(I)=ln[T(I)],Y(I)=ln[-R(I)] (I=1,N+1) 调用线性回归子程序计算 A,B (反应级数 S=B,速率常数 KS=EXP(A))N) 输出: A,B, S,KS 结束

SS=EXP(A) WRITE(6 IDA BRS SS 11 D1810/5XB=D18.10,5XR=,D18.10& D1 810,5X,k=D18.100 END SUBROUTINE CF(N,H,X,Y,Z) DIMENSION X(N),Y(N).Z(N) DOUBLEPRECISIONX.Y.Z.H.T.YA.YB T=X(1)+H CALL LGRG2(X.YN.TYAY T=X(1+2*H CALL LGRGZ(X YNTYBY Z(I)-(4-YA-3*Y(I-YBYH) D0101-2,N- T=X(I-H CALLLGRG2X YNTYAY T-XOIH CALLLGRG2(X.Y.N.T.YB) Z(D)-(YB-YA)(2*H 10 CONTINUE T-XONH CALL LGRG2CX.Y.N.TYAY T=X(N)2*H CALLLGRG2(X.Y.N.T.YB) Z(N(3*Y(N)4*YA+YB)(2*H) RETURN END SUBROUTINE PK(N.X.Y.A,B,R) DOUBLEPRECISIONX.Y.A.B.R DIMENSION X(N)Y(N) SX=0.0 8V=00 SXX=00 SYY-0.0 SXY-0.0 DO 10I=LN X1=X① Y1-Y0) SX-SX+XI SY-SY+Y1 SXX=SXX+XI*X SYY=SYY+Y1*YI
SS=EXP(A) WRITE(6,11)A,B,R,S,SS 11 FORMAT(/5X,'A=',D18.10//5X,'B=',D18.10, 5X,'R=',D18.10// & 5X,'n=',D18.10,5X,'k=',D18.10/) END SUBROUTINE CF(N,H,X,Y,Z) DIMENSION X(N),Y(N),Z(N) DOUBLE PRECISION X,Y,Z,H,T,YA,YB T=X(1)+H CALL LGRG2(X,Y,N,T,YA) T=X(1)+2*H CALL LGRG2(X,Y,N,T,YB) Z(1)=(4*YA-3*Y(1)-YB)/(2*H) DO 10 I=2,N-1 T=X(I)-H CALL LGRG2(X,Y,N,T,YA) T=X(I)+H CALL LGRG2(X,Y,N,T,YB) Z(I)=(YB-YA)/(2*H) 10 CONTINUE T=X(N)-H CALL LGRG2(X,Y,N,T,YA) T=X(N)-2*H CALL LGRG2(X,Y,N,T,YB) Z(N)=(3*Y(N)-4*YA+YB)/(2*H) RETURN END SUBROUTINE PK(N,X,Y,A,B,R) DOUBLE PRECISION X,Y,A,B,R DIMENSION X(N),Y(N) SX=0.0 SY=0.0 SXX=0.0 SYY=0.0 SXY=0.0 DO 10 I=1,N X1=X(I) Y1=Y(I) SX=SX+X1 SY=SY+Y1 SXX=SXX+X1*X1 SYY=SYY+Y1*Y1

SXY=SXY+X1*YI 10 CONTINUE DXX SXX-SX*SX/N DYY=SYY-SY+SY/N DXY=SXY-SXSY/N B=DXYDXX A=(SY-B*SXVN R=DXY/SQRT(DXX*DYY) RETURN END SUBROUTINE LGRG2(X YNTZY DIMENSION X(N).Y(N) DOUBLE PRECISIONX.Y.T.Z.S Z=0.0 IF(N.LE.0)RETURN IF(N.EO.1)THEN 7=Y1) RETURN END IF IF(N.EQ.2)THEN Z-(Y(1)*(T-X(2yY(2)*(T-X1)MX(1X2》 RETURN ENDIE IF(T.LE.X(2)YTHEN K=1 M=3 ELSE IF(T.GE.X(N-1))THEN K=N-2 ELSE K=1 M=N 10 IF(IABS(K-M).NE.I)THEN L=(K+M)2 IF(T.I T.X(L))THEN M=L ELse K=1 ENDIE G0T010 END IF IF(ABS(T-X(K)).LT.ABS(T-X(M)))THEN K=K-1
SXY=SXY+X1*Y1 10 CONTINUE DXX=SXX-SX*SX/N DYY=SYY-SY*SY/N DXY=SXY-SX*SY/N B=DXY/DXX A=(SY-B*SX)/N R=DXY/SQRT(DXX*DYY) RETURN END SUBROUTINE LGRG2(X,Y,N,T,Z) DIMENSION X(N),Y(N) DOUBLE PRECISION X,Y,T,Z,S Z=0.0 IF(N.LE.0)RETURN IF(N.EQ.1)THEN Z=Y(1) RETURN END IF IF(N.EQ.2)THEN Z=(Y(1)*(T-X(2))-Y(2)*(T-X(1)))/(X(1)-X(2)) RETURN END IF IF(T.LE.X(2))THEN K=1 M=3 ELSE IF(T.GE.X(N-1))THEN K=N-2 M=N ELSE K=1 M=N 10 IF(IABS(K-M).NE.1)THEN L=(K+M)/2 IF(T.LT.X(L))THEN M=L ELSE K=L ENDIF GOTO 10 END IF IF(ABS(T-X(K)).LT.ABS(T-X(M))) THEN K=K-1

ELSE M=M+1 DIF Z=0.0 D030=K,M g=10 DO 20 I=K M IF(.NE.I)THEN S=S*(T-X(J)(X(I)-X(J)) END IF 20 CONTINUE Z=7+S*Y1) 30 CONTINUE RETURN END 4运行结果。(12分) A=-1689023923D+02 B= .2122376481D+01 R :.9989326504D+00 n 2122376481D+01 k=4620216268D-07 动力学方程式为: v=-业=(m 2122376481D+01k= 4620216268D-07) dt C 1.计算原理(化学原理和计算方法)(12分) 反应 2A2广B A+C>D 其动力学方程式为
ELSE M=M+1 END IF END IF Z=0.0 DO 30 I=K,M S=1.0 DO 20 J=K,M IF(J.NE.I)THEN S=S*(T-X(J))/(X(I)-X(J)) END IF 20 CONTINUE Z=Z+S*Y(I) 30 CONTINUE RETURN END 4.运行结果。(12 分) A= -.1689023923D+02 B= .2122376481D+01 R= .9989326504D+00 n= .2122376481D+01 k= .4620216268D-07 动力学方程式为: n kp t p = − = d d ν (n= .2122376481D+01 k= .4620216268D-07) C 1.计算原理(化学原理和计算方法)(12 分) 反应 k1 k2 2A B A + C ⎯⎯→3 D k 其动力学方程式为:

d[A] d =-[A]+[B]-%[A]IC] d(B]-&,[A]-k;[B] C]=-k,IAJIC] D]=&,[AJIC] dt 利用Runge-Kutta法解此方程组,可得不同时刻的[A,B],[C],D]值。 2.程序框图(18分) 开始 输入:[A],B,[C],D初值 时间间隔H 计算精度EPS 计算:积分步长H0 调用变步长Runge-.Kuta积分法子程序解动力学方程组计算时刻t 的ABC,D (其中调用计算动力学方程组的子程序计算DY值)》 列表输出:0-200min内每隔10min所对应的A,B),[C,D]值 3.源程序(18分) PROGRAM MAIN IMPLICITREAL*8(A-H.O-Z) DIMENSION YO(10).Y1(10),Y2(10) OPEN(6,FILE-TESTC.TXT,STATUS-UNKNOWN) DATA Y0/2.0,0.0,1.0.0.0.6*0.0/ N=4 T0-0.0 T1=100.0 H0=10 EPS=1.0E-6 H=HO WRITE(6.11)N.T0.T1.H0.EPS WRITE(6.22)T0.H.(Y0(D).1=1.N) M=IDINT((T1-T0VHO+10) D08010=1,M K=1
[A][C] d d[D] [A][C] d d[C] [A] [B] d d[B] [A] [B] [A][C] d d[A] 3 3 2 2 1 2 3 2 1 k t k t k k t k k k t = = − = − = − + − 利用 Runge-Kutta 法解此方程组,可得不同时刻的[A],[B],[C],[D]值。 2.程序框图(18 分) 3.源程序(18 分) PROGRAM MAIN IMPLICIT REAL *8(A-H,O-Z) DIMENSION Y0(10),Y1(10),Y2(10) OPEN(6,FILE='TESTC.TXT',STATUS='UNKNOWN') DATA Y0/2.0,0.0,1.0,0.0,6*0.0/ N=4 T0=0.0 T1=100.0 H0=10 EPS=1.0E-6 H=H0 WRITE(6,11)N,T0,T1,H0,EPS WRITE(6,22)T0,H,(Y0(I),I=1,N) M=IDINT((T1-T0)/H0+10) DO 80 I0=1,M K=1 开始 输入:[A],[B],[C],[D]初值 时间间隔 H, 计算精度 EPS 计算:积分步长 H0 调用变步长 Runge-Kutta 积分法子程序解动力学方程组计算时刻 t 的[A],[B],[C],[D]值 (其中调用计算动力学方程组的子程序计算 DY 值) 列表输出:0-200min 内每隔 10min 所对应的[A],[B],[C],[D]值 结束

CALLRK4(TO.Y0.Y1.HO.N.K) D030KK=1,100 CALL RK4(TO,YO.Y2.,H.N.K) ES=0.0 DO10EIN ES=ES+ABS((Y2(J)-Y1(J)V/Y2(J) IF(ES.LT.EPS)G 0T050 D020J=1,N 20 YI(Y2() CONTINUE WRITE(6.33) STOP 50 T0=T0+H0 D060J=1.N YO(J)=Y2(J) WRITE(6 22TO HCY20DI=LN) WRITE(6.44) FORMAT(/1XN=,2,2X'T0=,F6.1,2XT1=,F8.1,2X,& H0=,G83,1XEPS=,G10.320X,Y0,=1,2,3,4,N”& 1X.66(1H-)/5X.'t/min'.3X.'H/min'.6X.'[Al/molL-1' 6X.[B/molL-I.6X.[Cl/molL-I.6X.[Dl/molL-1/1X.66(1H-)) 2 FORMAT(IX.2F822X.4GI5.6) FORMAT(/1X,'FAILED TO FIND STABLE SOLUTION IN MAX IT/) FORMAT(1X.66(1H-)) END SUBROUTINE F(Y.DY) IMPLICIT REAL *8A-H0-Z REAL8 KI.K2.K3 DIMENSION Y(10LDY(10) DATA K1/0.0138/K2/2.76E-04/K3/7.2E-04/ DY(1=K1*Y(1)*YI+K2*Y(2K3*Y(1)*Y3) DY(2-K1Y()Y()-K2-Y(2) DY(3=K3*Y(1)*Y(3) DY(4)=K3*Y(1)*Y(3) RETURN END SUBROUTINERK4(X0,Y0.Y.H.N.M IMPLICIT REAL 8(A-H.O-Z) DIMENSION YO(N).Y(N)
CALL RK4(T0,Y0,Y1,H0,N,K) DO 30 KK=1,100 K=K+K H=H0/K CALL RK4(T0,Y0,Y2,H,N,K) ES=0.0 DO 10 J=1,N 10 ES=ES+ABS((Y2(J)-Y1(J))/Y2(J)) IF(ES.LT.EPS)GOTO 50 DO 20 J=1,N 20 Y1(J)=Y2(J) 30 CONTINUE WRITE(6,33) STOP 50 T0=T0+H0 DO 60 J=1,N 60 Y0(J)=Y2(J) WRITE(6,22)T0,H,(Y2(I),I=1,N) 80 CONTINUE WRITE(6,44) 11 FORMAT(/1X,'N=',I2,2X,'T0=',F6.1,2X,'T1=',F8.1,2X, & 'H0=',G8.3,1X,'EPS=',G10.3//20X,'Y(I),I=1,2,3,4,...,N' & 1X,66(1H-)/5X,'t/min',3X,'H/min',6X,'[A]/molL-1', & 6X,'[B]/molL-1',6X,'[C]/molL-1',6X,'[D]/molL-1'/1X,66(1H-)) 22 FORMAT(1X,2F8.2,2X,4G15.6) 33 FORMAT(/1X,'FAILED TO FIND STABLE SOLUTION IN MAX IT'/) 44 FORMAT(1X,66(1H-)) END SUBROUTINE F(Y,DY) IMPLICIT REAL *8(A-H,O-Z) REAL *8 K1,K2,K3 DIMENSION Y(10),DY(10) DATA K1/0.0138/,K2/2.76E-04/,K3/7.2E-04/ DY(1)=-K1*Y(1)*Y(1)+K2*Y(2)-K3*Y(1)*Y(3) DY(2)=K1*Y(1)*Y(1)-K2*Y(2) DY(3)=-K3*Y(1)*Y(3) DY(4)=K3*Y(1)*Y(3) RETURN END SUBROUTINE RK4(X0,Y0,Y,H,N,M) IMPLICIT REAL *8(A-H,O-Z) DIMENSION Y0(N),Y(N)