
《空间解析几何》课程教学大纲 一、课程基本信息 课程代码:16110802 课程名称:空间解析几何 英文名称: Analytic Geometry 课程类别:专业基础课 学 时:30 分:2 适用对象:数学类本科 考核方式:考试 先修课程:无 二、课程简介 《空间解析几何》是数学类专业的一门专业基础课程,是用代数的方法研究几何 图形的一门学科,是初等数学进入高等数学的转折点,是沟通几何形式与数学关系的 一座桥梁。线性代数、数学分析、微分方程、高等几何等课程的学习都离不开空间解 析几何的基本知识及研究方法。《空间解析几何》内容包括:空间直角坐标、平面和 直线,向量代数, 二次曲面等。通过空间解析几何课程的学习,不仅可以使学生理解 解析几何的基本概念和基本理论,树立空间的概念,掌握运用代数方法讨论一些简单 的图形和变形的性质,加深对中学几何理论与方法的理解。更重要的是培养学生的几 何直观能力、逻辑推理能力、空间想象能力、认识事物的能力、综合运用所学的知识 来分析和解决实际问题的能力,为进一步学习其他课程打下基础。另一方面,空间解 析几何在代数、分析、力学、物理和一些工程技术中都有广泛的应用,是解决某些实 际问题的基础。 Analytic Geometry is a professional basic course for mathematics majors.It is a subject to study geometric figures by means of algebra.It is a tuming point for elementary mathematics to enter higher mathematics and a bridge between geometric forms and mathematics.Linear algebra,mathematical analysis,differential equations,advanced geometry and other courses are inseparable from the basic knowledge and research methods of analytic geometry.Analytic geometry includes:space rectangular coordinates,plane and line,vector algebra,quadric surface,etc.Through the study of this course,students can not only understand the basic concepts and theories of analytic geometry,establish the concep of space,master the use of algebraic methods to discuss some simple graphics and deformation properties,and deepen the understanding of middle school geometry theory
1 《空间解析几何》课程教学大纲 一、课程基本信息 课程代码: 16110802 课程名称: 空间解析几何 英文名称: Analytic Geometry 课程类别: 专业基础课 学 时: 30 学 分: 2 适用对象: 数学类本科 考核方式:考试 先修课程:无 二、课程简介 《空间解析几何》是数学类专业的一门专业基础课程,是用代数的方法研究几何 图形的一门学科,是初等数学进入高等数学的转折点,是沟通几何形式与数学关系的 一座桥梁。线性代数、数学分析、微分方程、高等几何等课程的学习都离不开空间解 析几何的基本知识及研究方法。《空间解析几何》内容包括:空间直角坐标、平面和 直线,向量代数,二次曲面等。通过空间解析几何课程的学习,不仅可以使学生理解 解析几何的基本概念和基本理论,树立空间的概念,掌握运用代数方法讨论一些简单 的图形和变形的性质,加深对中学几何理论与方法的理解。更重要的是培养学生的几 何直观能力、逻辑推理能力、空间想象能力、认识事物的能力、综合运用所学的知识 来分析和解决实际问题的能力,为进一步学习其他课程打下基础。另一方面,空间解 析几何在代数、分析、力学、物理和一些工程技术中都有广泛的应用,是解决某些实 际问题的基础。 Analytic Geometry is a professional basic course for mathematics majors. It is a subject to study geometric figures by means of algebra. It is a turning point for elementary mathematics to enter higher mathematics and a bridge between geometric forms and mathematics. Linear algebra, mathematical analysis, differential equations, advanced geometry and other courses are inseparable from the basic knowledge and research methods of analytic geometry. Analytic geometry includes: space rectangular coordinates, plane and line, vector algebra, quadric surface, etc. Through the study of this course, students can not only understand the basic concepts and theories of analytic geometry, establish the concept of space, master the use of algebraic methods to discuss some simple graphics and deformation properties, and deepen the understanding of middle school geometry theory

and methods.What's more important is to cultivate students'ability of geometric intuition, logical reasoning,spatial imagination,understanding things,and comprehensive use of knowledge to analyze and solve practical problems,so as to lay a foundation for further study of other courses.On the other hand.analytic geometry is widely used in algebra. analysis.mechanics.physics and some engineering technologies.and it is also the basis of solving some practical problems. 三、课程性质与教学目的 课程性质:专业基础课 教学目的:掌握解析几何的基本思想、内容和方法,较熟练地掌握树立起空间的 概念,受到几何直观和逻辑推理等方面的训练。扩大知识领域,培养想象能力以 及运用代数方法讨论一些简单的图形和变形的性质,为进一步学习其他课程打下 基础。另一方面,加深对中学几何理论与方法的理解,从而获得在比较高的观点 下处理几何问题的能力,借助解析几何所具有的较强的直观效果提高学生认识事 物的能力。通过介绍空间解析几何在现代桥梁设计、动漫游戏,星际飞行、自动 目标识别与导航等领域所发挥的重要作用以及我国所取得的巨大成就,让学生感 受到民族的自豪感和对中因文化的认同感,激起强烈的民族责任感,让学生在课 堂上不仅可以学到知识,还可以开拓境界,熏陶心灵,引导学生树立正确的世界 观、人生观和价值观,更好地为学生成长服务。 四、教学内容及要求 第一章向量 (一)目的与要求 1.正确理解向量的有关概念,并掌握向量的线性运算及其运算规律。 2.理解向量内积、外积运算的定义,掌握它们的运算规律和熟悉它们的几 何性质。 3.熟练进行向量的各种运算,并能利用向量的坐标来解决一些几何问题。 〖重点与难点】 1.本章的重点内容:内积、外积与混合积的定义、运算规律及几何性质 2.本章的难点内容:混合积与双重外积的运算规律与性质。 (二)教学内容 第一节向量及其线性运算 1.主要内容
2 and methods. What's more important is to cultivate students' ability of geometric intuition, logical reasoning, spatial imagination, understanding things, and comprehensive use of knowledge to analyze and solve practical problems, so as to lay a foundation for further study of other courses. On the other hand, analytic geometry is widely used in algebra, analysis, mechanics, physics and some engineering technologies, and it is also the basis of solving some practical problems. 三、课程性质与教学目的 课程性质:专业基础课 教学目的:掌握解析几何的基本思想、内容和方法,较熟练地掌握树立起空间的 概念,受到几何直观和逻辑推理等方面的训练。扩大知识领域,培养想象能力以 及运用代数方法讨论一些简单的图形和变形的性质,为进一步学习其他课程打下 基础。另一方面,加深对中学几何理论与方法的理解,从而获得在比较高的观点 下处理几何问题的能力,借助解析几何所具有的较强的直观效果提高学生认识事 物的能力。通过介绍空间解析几何在现代桥梁设计、动漫游戏,星际飞行、自动 目标识别与导航等领域所发挥的重要作用以及我国所取得的巨大成就,让学生感 受到民族的自豪感和对中国文化的认同感,激起强烈的民族责任感,让学生在课 堂上不仅可以学到知识,还可以开拓境界,熏陶心灵,引导学生树立正确的世界 观、人生观和价值观,更好地为学生成长服务。 四、教学内容及要求 第一章 向量 (一)目的与要求 1.正确理解向量的有关概念,并掌握向量的线性运算及其运算规律。 2.理解向量内积、外积运算的定义,掌握它们的运算规律和熟悉它们的几 何性质。 3.熟练进行向量的各种运算,并能利用向量的坐标来解决一些几何问题。 〖重点与难点〗 1.本章的重点内容:内积、外积与混合积的定义、运算规律及几何性质。 2.本章的难点内容:混合积与双重外积的运算规律与性质。 (二)教学内容 第一节 向量及其线性运算 1.主要内容

向量的定义及表示 2.基本概念和知识点 基本概念:数量,向量,有向线段,反向量 知识点:向量平移不变性 3.问题与应用 第二节向量加法 1.主要内容 向量的加法和减法运算 2.基本概念和知识点 基本概念:向量的和,零向量,向量差 知识点:三角形法则,平行四边形法则,多边形法则,三角形不等式 3.问题与应用 第三节数乘向量 1.主要内容 数乘向量的定义及运算规律 2.基本概念和知识点 基本概念:共线向量,共面向量,数乘向量 知识点:数乘向量的运算规律 3.问题与应用 第四节向量的坐标 1.主要内容 向量的坐标表示及计算 2.基本概念和知识点 基本概念:基本向量,定位向量,线性组合,向量的坐标, 知识点:向量运算的坐标表示 3.问题与应用 第二节内积 1.主要内容 内积的定义、性质及运算规律,点到平面的距离 2.基本概念和知识点 基本概念:夹角,内积,投影,水平支量,垂直支量,内支量,外支量
3 向量的定义及表示 2.基本概念和知识点 基本概念:数量,向量,有向线段,反向量 知识点:向量平移不变性 3.问题与应用 第二节 向量加法 1.主要内容 向量的加法和减法运算 2.基本概念和知识点 基本概念:向量的和,零向量,向量差, 知识点:三角形法则,平行四边形法则,多边形法则,三角形不等式 3.问题与应用 第三节 数乘向量 1.主要内容 数乘向量的定义及运算规律 2.基本概念和知识点 基本概念:共线向量,共面向量,数乘向量 知识点:数乘向量的运算规律 3.问题与应用 第四节 向量的坐标 1.主要内容 向量的坐标表示及计算 2.基本概念和知识点 基本概念:基本向量,定位向量,线性组合,向量的坐标, 知识点:向量运算的坐标表示 3.问题与应用 第二节 内积 1.主要内容 内积的定义、性质及运算规律,点到平面的距离 2.基本概念和知识点 基本概念:夹角,内积,投影,水平支量,垂直支量,内支量,外支量

知识点:夹角的性质,内积的交换律、结合律、分配律 3.问题与应用 应用:掌握内积的运算并能利用内积解决一些几何问题。 第三节外积 1.主要内容 外积的定义、运算规律及其几何意义 2.基本概念和知识点 概念:向量组的左手系、右手系,外积, 知识点:外积的运算规律,外积的几何意义 3.问题与应用 应用:点到直线的距离,两平行直线间的距离 第四节混合积与双重外积 1.主要内容 利用向量坐标计算体积 2.基本概念和知识点 基本概念:体积,平行坐标系,对偶坐标系 知识点:体积的性质,三向量共面的充要条件,双重外积的展开定理 3.问题与应用 应用:利用体积公式计算四面体或平行六面体的体积。 (三)思考与实践 勤学多练。 (四)教学方法与手段 课堂讲授为主,学生复习、辅导为辅。 第二章平面与直线 (一)目的与要求 1.理解平面与空间直线的各种形式的方程以及方程中的系数或常数项的 几何意义 2.掌握平面方程和直线方程各种形式的相互转换。 3.充分理解空间直线可以看成两个平面的交线,并用这两平面方程构成 的方程组来表示。 4.熟练地根据平面和空间直线以及点的坐标判别有关点,平面,直线之 4
4 知识点:夹角的性质,内积的交换律、结合律、分配律 3.问题与应用 应用:掌握内积的运算并能利用内积解决一些几何问题。 第三节 外积 1.主要内容 外积的定义、运算规律及其几何意义 2.基本概念和知识点 概念:向量组的左手系、右手系,外积, 知识点:外积的运算规律,外积的几何意义 3.问题与应用 应用:点到直线的距离,两平行直线间的距离 第四节 混合积与双重外积 1.主要内容 利用向量坐标计算体积 2.基本概念和知识点 基本概念:体积,平行坐标系,对偶坐标系 知识点:体积的性质,三向量共面的充要条件,双重外积的展开定理 3.问题与应用 应用:利用体积公式计算四面体或平行六面体的体积。 (三)思考与实践 勤学多练。 (四)教学方法与手段 课堂讲授为主,学生复习、辅导为辅。 第二章 平面与直线 (一)目的与要求 1. 理解平面与空间直线的各种形式的方程以及方程中的系数或常数项的 几何意义。 2. 掌握平面方程和直线方程各种形式的相互转换。 3. 充分理解空间直线可以看成两个平面的交线,并用这两平面方程构成 的方程组来表示。 4. 熟练地根据平面和空间直线以及点的坐标判别有关点,平面,直线之

间的位置关系和计算它们之间的距离与交角。 〖重点与难点】 1.本章的重点内容:直线的点向方程和一般方程,平面方程和直线方程 各种形式的相互转换。 2.本章的难点内容:平面方程和直线方程的位置关系。 (二)教学内容 第一节空间直角坐标 1.主要内容 坐标系的建立,点的坐标,向量的坐标表示及计算 2.基本极念和知识点 基本概念:坐标轴、坐标平面, 知识点:坐标系的平移,两点间的距离公式 3.问题与应用 第二节平面方程 1.主要内容 平面的点法式方程和一般方程 2.基本概念和知识点 基本概念:法向,平面的点法式方程,平面的一般方程 知识点:两平面的的位置关系 3.问题与应用 问题:抹掉平面方程的一个一次项,对平面的位置有什么影响? 第三节空间直线方程 1.主要内容 直线的参数方程、点向(标准)方程与一般方程,两直线间的夹角 2.基本概念和知识点 基本概念:参数方程,点向方程,一般方程 知识点:三种直线方程之间的相互转化,两直线间的夹角公式 3.问题与应用 问题:如何求直线在一般平面(非坐标平面)上的投影?
5 间的位置关系和计算它们之间的距离与交角。 〖重点与难点〗 1. 本章的重点内容:直线的点向方程和一般方程,平面方程和直线方程 各种形式的相互转换。 2. 本章的难点内容:平面方程和直线方程的位置关系。 (二)教学内容 第一节 空间直角坐标 1.主要内容 坐标系的建立,点的坐标,向量的坐标表示及计算 2.基本概念和知识点 基本概念:坐标轴、坐标平面, 知识点:坐标系的平移,两点间的距离公式 3.问题与应用 第二节 平面方程 1. 主要内容 平面的点法式方程和一般方程 2.基本概念和知识点 基本概念:法向,平面的点法式方程,平面的一般方程 知识点:两平面的的位置关系 3.问题与应用 问题:抹掉平面方程的一个一次项,对平面的位置有什么影响? 第三节 空间直线方程 1.主要内容 直线的参数方程、点向(标准)方程与一般方程,两直线间的夹角 2.基本概念和知识点 基本概念:参数方程,点向方程,一般方程 知识点:三种直线方程之间的相互转化,两直线间的夹角公式 3.问题与应用 问题:如何求直线在一般平面(非坐标平面)上的投影?

第四节直线与平面的有关问题 1.主要内容 平面与直线之间的位置关系以及它们之间的交角,两直线间的位置关系 2.基本概念和知识点 基本概念:直线与平面平行、相交,两直线共面与异面 知识点:直线与平面,直线与直线的位置关系 3.问题与应用 应用:判断空间中两条直线的位置关系 第五节距离 1.主要内容 点到平面的距离,点到直线的距离,两异面直线间的距离 2.基本概念和知识点 基本概念:公垂线 知识点:点到平面的距离公式,点到直线的距离公式,两异面直线间的 距离公式 3.问题与应用 应用:求空间中两条异面直线之间的距离以及公垂线方程 (三)思考与实践 勤学多练。 (四)教学方法与手段 课堂讲授为主,学生复习、辅导为辅。 第三章特殊曲面与二次曲面 (一)目的与要求 1.掌握求柱面、锥面与旋转面的方程的一般方法与步骤。 2.能熟练地从曲面的方程来识别满足柱面、锥面、旋转面的几何特征。 3.掌握椭球面、双曲面与抛物面的主要性质,并能从它们的标准方程画出 它们的图形。 〖重点与难点】 1.本章的重点内容:熟练地从曲面的方程来识别满足柱面、锥面、旋转面 6
6 第四节 直线与平面的有关问题 1.主要内容 平面与直线之间的位置关系以及它们之间的交角,两直线间的位置关系 2.基本概念和知识点 基本概念:直线与平面平行、相交,两直线共面与异面 知识点:直线与平面,直线与直线的位置关系 3.问题与应用 应用:判断空间中两条直线的位置关系 第五节 距离 1.主要内容 点到平面的距离,点到直线的距离,两异面直线间的距离 2.基本概念和知识点 基本概念:公垂线 知识点:点到平面的距离公式,点到直线的距离公式,两异面直线间的 距离公式 3.问题与应用 应用:求空间中两条异面直线之间的距离以及公垂线方程 (三)思考与实践 勤学多练。 (四)教学方法与手段 课堂讲授为主,学生复习、辅导为辅。 第三章 特殊曲面与二次曲面 (一)目的与要求 1.掌握求柱面、锥面与旋转面的方程的一般方法与步骤。 2.能熟练地从曲面的方程来识别满足柱面、锥面、旋转面的几何特征。 3.掌握椭球面、双曲面与抛物面的主要性质,并能从它们的标准方程画出 它们的图形。 〖重点与难点〗 1. 本章的重点内容:熟练地从曲面的方程来识别满足柱面、锥面、旋转面

的几何特征,掌握椭球面、双曲面与抛物面的主要性质,并能从它们的 标准方程画出它们的图形 2.本章的难点内容:掌握椭球面、双曲面与抛物面的主要性质,并能从它 们的标准方程画出它们的图形。 (二)教学内容 第一节曲面与方程球面、直圆柱面和直圆锥面的方程 1.主要内容 球面方程、直圆柱面方程与直锥面方程的表示 2.基本概念和知识点 基本概念:空间中曲面和曲线的一般方程 知识点:空间中圆的表示 3.问题与应用 问题:如果两条直线平行,相交以及异面(不垂直),其中一条直线绕着 外一条直线旋转,得到的旋转曲面分别是什么? 第二节曲线族产生曲面的理论柱面、锥面及旋转曲面的方程 1.主要内容 柱面、锥面、旋转曲面方程的建立以及曲线在坐标平面上的投影 2.基本概念和知识点 基本概念:投影,投影柱面,中心二次曲面,无心二次曲面 知识点:椭球面、双曲面与抛物面的标准方程及几何性质 3.问题与应用 问题1:在典型二次曲面中,哪些曲面是由直线族生成的? 问题2:如何求空间曲线在一般平面(非坐标平面)上的投影? 应用1:熟练利用消元法求曲线在坐标平面的投影。 应用2:熟练利用“平行截割法”来认识空间曲面的大致形状。 (三)思考与实践 勤学多练。 (四)教学方法与手段 课堂讲授为主,学生复习、辅导为辅
7 的几何特征,掌握椭球面、双曲面与抛物面的主要性质,并能从它们的 标准方程画出它们的图形。 2. 本章的难点内容:掌握椭球面、双曲面与抛物面的主要性质,并能从它 们的标准方程画出它们的图形。 (二)教学内容 第一节 曲面与方程球面、直圆柱面和直圆锥面的方程 1.主要内容 球面方程、直圆柱面方程与直锥面方程的表示 2.基本概念和知识点 基本概念:空间中曲面和曲线的一般方程 知识点: 空间中圆的表示 3.问题与应用 问题:如果两条直线平行,相交以及异面(不垂直),其中一条直线绕着另 外一条直线旋转,得到的旋转曲面分别是什么? 第二节 曲线族产生曲面的理论柱面、锥面及旋转曲面的方程 1.主要内容 柱面、锥面、旋转曲面方程的建立以及曲线在坐标平面上的投影 2.基本概念和知识点 基本概念:投影,投影柱面,中心二次曲面,无心二次曲面 知识点:椭球面、双曲面与抛物面的标准方程及几何性质 3.问题与应用 问题 1:在典型二次曲面中,哪些曲面是由直线族生成的? 问题 2:如何求空间曲线在一般平面(非坐标平面)上的投影? 应用 1:熟练利用消元法求曲线在坐标平面的投影。 应用 2:熟练利用“平行截割法”来认识空间曲面的大致形状。 (三)思考与实践 勤学多练。 (四)教学方法与手段 课堂讲授为主,学生复习、辅导为辅
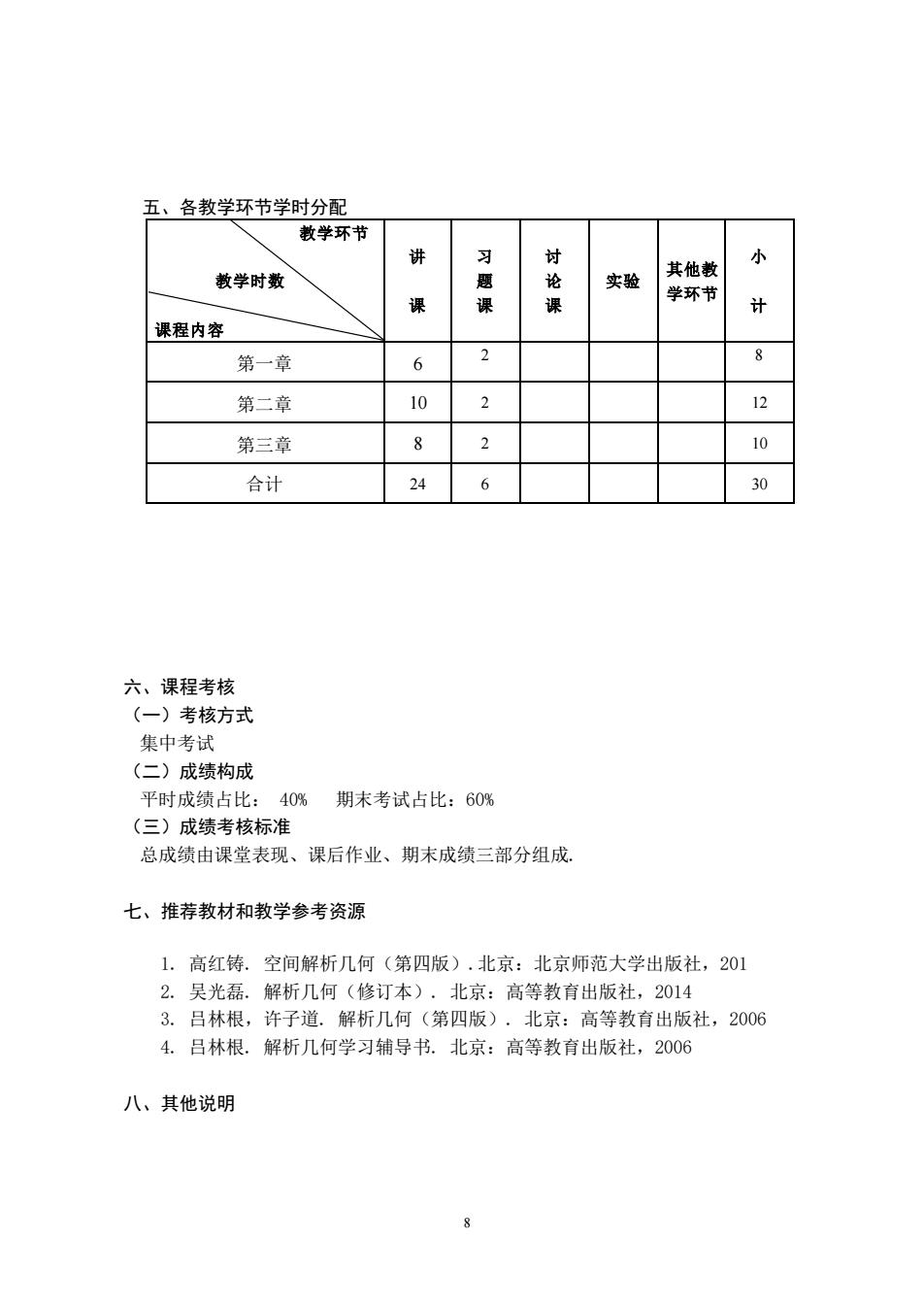
五、各教学环节学时分配 教学环节 的 习 讨 小 教学时数 实验 其他教 课 学环节 课程内容 第一章 6 8 第二章 10 2 12 第三章 2 10 合计 24 6 30 六、课程考核 (一)考核方式 集中考试 (二)成绩构成 平时成绩占比:40% 期末考试占比:60% (三)成绩考核标准 总成绩由课堂表现、课后作业、期末成绩三部分组成。 七、推荐教材和教学参考资源 1.高红铸.空间解析几何(第四版).北京:北京师范大学出版社,201 2.吴光磊.解析几何(修订本).北京:高等教育出版社,2014 3.吕林根,许子道.解析几何(第四版),北京:高等教育出版社,2006 4.吕林根.解析几何学习辅导书.北京:高等教育出版社,2006 八、其他说明 8
8 五、各教学环节学时分配 教学环节 教学时数 课程内容 讲 课 习 题 课 讨 论 课 实验 其他教 学环节 小 计 第一章 6 2 8 第二章 10 2 12 第三章 8 2 10 合计 24 6 30 六、课程考核 (一)考核方式 集中考试 (二)成绩构成 平时成绩占比: 40% 期末考试占比:60% (三)成绩考核标准 总成绩由课堂表现、课后作业、期末成绩三部分组成. 七、推荐教材和教学参考资源 1. 高红铸. 空间解析几何(第四版).北京:北京师范大学出版社,201 2. 吴光磊. 解析几何(修订本). 北京:高等教育出版社,2014 3. 吕林根,许子道. 解析几何(第四版). 北京:高等教育出版社,2006 4. 吕林根. 解析几何学习辅导书. 北京:高等教育出版社,2006 八、其他说明

大纲修订人:彭小明 修订日期:2022年9月 大纲审定人:刘国刚 审定日期:2022年9月 9
9 大纲修订人: 彭小明 修订日期:2022 年 9 月 大纲审定人: 刘国刚 审定日期:2022 年 9 月