
《复变函数》课程教学大纲◆ 一、课程基本信息 课程代码:16183703 课程名称:复变函数 英文名称:Complex Variables 课程类别:专业课 时:48 学分:3 适用对象:数学与应用数学 考核方式:考查 先修课程:《数学分析》、《解析几何》、《高等代数》 二、课程简介 本课程是数学与应用数学专业的一门专业选修课.课程主要讲授单复变函数的 些基本知识,分别从导数、积分、级数、留数、映射五个方面来刻画解析函数的性 质及其应用。首先从复数域开始,引入复变函数,再给出解析函数的概念,再以它为 研究对象,介绍解析函数的导数、积分、解析函数的幂级数表示法,解析函数的罗朗 展式与孤立奇点,留数理论及其应用。《复变函数论》主要讲单复变中的解析函数理 论:内容包括解析函数的概念、性质、柯西一黎曼条件。柯西积分定理及柯西积分公 式。解析函数的泰勒展式和罗朗展式。利用留数理论求积分,保形映射等内容。 This course is a specialized elective course in mathematics an applied mathematics.The course mainly introduces some basic knowledge of single complex functions describing the properties and applications of analytical functions from five aspects:derivative,integral,series,residue and mapping respectively.First of all,from the complex domain,the complex variable function is introduced,and then the concept of analytic function is given. Taking it as the research object,we introduce the derivative,integral,power series representation,Laurent expansions,isolated singularity,residue theory of analytic function and its application.The theory of complex variable mainly focuses on the analytic function theory of simple complex variables: the content includes the concept and property of analytic function, Cauchy-Riemann condition.Cauchy integral theorem and Cauchy integral formula
1 《复变函数》课程教学大纲◆ 一、课程基本信息 课程代码:16183703 课程名称:复变函数 英文名称:Complex Variables 课程类别:专业课 学 时:48 学 分:3 适用对象: 数学与应用数学 考核方式:考查 先修课程:《数学分析》、《解析几何》、《高等代数》 二、课程简介 本课程是数学与应用数学专业的一门专业选修课. 课程主要讲授单复变函数的 一些基本知识,分别从导数、积分、级数、留数、映射五个方面来刻画解析函数的性 质及其应用。首先从复数域开始,引入复变函数,再给出解析函数的概念,再以它为 研究对象,介绍解析函数的导数、积分、解析函数的幂级数表示法,解析函数的罗朗 展式与孤立奇点,留数理论及其应用。《复变函数论》主要讲单复变中的解析函数理 论:内容包括解析函数的概念、性质、柯西一黎曼条件。柯西积分定理及柯西积分公 式。解析函数的泰勒展式和罗朗展式。利用留数理论求积分,保形映射等内容。 This course is a specialized elective course in mathematics an applied mathematics. The course mainly introduces some basic knowledge of single complex functions describing the properties and applications of analytical functions from five aspects: derivative, integral, series, residue and mapping, respectively. First of all, from the complex domain, the complex variable function is introduced, and then the concept of analytic function is given. Taking it as the research object, we introduce the derivative, integral, power series representation, Laurent expansions, isolated singularity, residue theory of analytic function and its application. The theory of complex variable mainly focuses on the analytic function theory of simple complex variables: the content includes the concept and property of analytic function, Cauchy-Riemann condition. Cauchy integral theorem and Cauchy integral formula

Taylor Expansion and Roland Expansion of Analytic Functions.Using the theory of residue for integration,conformal mapping and other contents. 三、课程性质与教学目的 复变函数论是数学系各专业的一门重要课程,同时又是数学分析的后继课。从数 学理论角度看,它是数学的重要分支之一,内容丰富而完美。同时,它在力学、电学 及理论物理等学科中有着重要的应用。复变函数理论起源和发展于16世纪的欧洲, 此后四百多年经历了大量的中西方学者的研究和推动,获得深刻发展。同时,复变函 数也是我国数学工作者从事研究最早也最有成效的数学分支之一。我国老一辈的数学 家在单复变函数及多复变函数方面做过许多重要工作。 本课程旨在使学生初步掌握复变函数的基本理论和方法,为学习有关后继课程和 进一步扩大数学知识面奠定必要的基础:了解国内外学者在复变理论科学研究的思想 和方法,发现科学研究的规律性、长期性和趣味性:了解国内数学家所做的重要工作, 以及老一辈数学家为复变函数理论的普及、应用,尤其结合当时社会经济发展,国防 发展的需要,克服很多困难所做的持续不断的努力。引导学生树立正确的价值观,坚 定“四个自信”,从思想上、政治上、行动上热爱祖国,积极响应党的号召,把个 人的前途和命运同国家和民族的前途和命运紧密联系起来,为中国特色社会主义伟大 事业培养合格的建设者和接班人。 四、教学内容及要求 第一章复变与复变函数 (一)目的与要求 1.了解复数的由来,复变函数学科诞生的学术问题背景,一些重要学者 做出的关键性进步贡献。理解复变函数学科发展的长期性、曲折性和 内在科学规律,以及在其他学科的广泛应用。 2。理解复数的概念,掌握复数的四则运算和共轭运算,会求非零复数的 模与辐角。 3.理解复平面、非零复数模与辐角的概念:了解无穷远点以及扩充复平 面的概念。 4.掌握区域、简单曲线、单连通区域与多连通区域等概念。 5.掌握用复变函数的方程来表示常用曲线以及用不等式表示区域。 6.掌握复变函数的概念,理解复变函数的极限与连续性。 2
2 Taylor Expansion and Roland Expansion of Analytic Functions. Using the theory of residue for integration, conformal mapping and other contents. 三、课程性质与教学目的 复变函数论是数学系各专业的一门重要课程,同时又是数学分析的后继课。从数 学理论角度看,它是数学的重要分支之一,内容丰富而完美。同时,它在力学、电学 及理论物理等学科中有着重要的应用。复变函数理论起源和发展于 16 世纪的欧洲, 此后四百多年经历了大量的中西方学者的研究和推动,获得深刻发展。同时,复变函 数也是我国数学工作者从事研究最早也最有成效的数学分支之一。我国老一辈的数学 家在单复变函数及多复变函数方面做过许多重要工作。 本课程旨在使学生初步掌握复变函数的基本理论和方法,为学习有关后继课程和 进一步扩大数学知识面奠定必要的基础;了解国内外学者在复变理论科学研究的思想 和方法,发现科学研究的规律性、长期性和趣味性;了解国内数学家所做的重要工作, 以及老一辈数学家为复变函数理论的普及、应用,尤其结合当时社会经济发展,国防 发展的需要,克服很多困难所做的持续不断的努力。引导学生树立正确的价值观,坚 定“四个自信”, 从思想上、政治上、行动上热爱祖国,积极响应党的号召,把个 人的前途和命运同国家和民族的前途和命运紧密联系起来,为中国特色社会主义伟大 事业培养合格的建设者和接班人。 四、教学内容及要求 第一章 复变与复变函数 (一)目的与要求 1. 了解复数的由来,复变函数学科诞生的学术问题背景,一些重要学者 做出的关键性进步贡献。理解复变函数学科发展的长期性、曲折性和 内在科学规律,以及在其他学科的广泛应用。 2. 理解复数的概念,掌握复数的四则运算和共轭运算,会求非零复数的 模与辐角。 3. 理解复平面、非零复数模与辐角的概念;了解无穷远点以及扩充复平 面的概念。 4. 掌握区域、简单曲线、单连通区域与多连通区域等概念。 5. 掌握用复变函数的方程来表示常用曲线以及用不等式表示区域。 6. 掌握复变函数的概念,理解复变函数的极限与连续性

(二)教学内容 第一节 1.复数集产生的历史背景(虚数的艰难被承认) 一真理性的东西一定可以经得住时间和空间的考验,最终占有自己的一席之地, 2.复数的定义。 3.复数域、复平面、复数的模与辐角、复数的乘幂与方根、共轭复数、 复数在几何上的应用举例 4.掌握复数的四则运算和共轭运算,模与辐角的概念及其运算性质:以 及复平面概念:掌握复数在几何上的应用(主要是灵活运用复数的向 量表示,并记住一些复曲线的参数方程,如连接两点云及E的线段、 直线的参数方程及圆的参数方程等)。 第二节 1.复平面上的点集 2.平面点集的几个基本概念、区域与若尔当曲线。 3.理解复平面点集的几个基本概念:掌握区域、单连通区域和多连通区 域,简单曲线等概念:理解约当曲线的概念并了解约当定理。 第三节 1.复变函数。 2.复变函数的概念、复变函数的极限与连续。 3.理解复变函数极限的概念,掌握极限等价的刻画定理1.2:理解复变 函数连续性的概念,掌握连续性等价的刻画定理1.3:理解有界闭集 上连续函数的三个性质。 第四节 1.复球面与无穷远点。 2.复球面、扩充复平面上的几个概念。 3.了解无穷远点以及扩充复平面的概念 (三)思老与实践 1.思考:复变函数的极限与连续性与实空间中函数极限、连续性的相同 点、不同点 2.实践:复数、复平面、复变函数的运用,具体问题的求解 (四)教学方法与手段 本章教学主要采用课堂讲授、多媒体教学、课堂讨论。 第二章解析函数 (一)目的与要求 3
3 (二)教学内容 第一节 1. 复数集产生的历史背景(虚数的艰难被承认) —真理性的东西一定可以经得住时间和空间的考验,最终占有自己的一席之地. 2. 复数的定义。 3. 复数域、复平面、复数的模与辐角、复数的乘幂与方根、共轭复数、 复数在几何上的应用举例。 4. 掌握复数的四则运算和共轭运算,模与辐角的概念及其运算性质;以 及复平面概念;掌握复数在几何上的应用(主要是灵活运用复数的向 量表示,并记住一些复曲线的参数方程,如连接两点 及 的线段、 直线的参数方程及圆的参数方程等)。 第二节 1.复平面上的点集。 2.平面点集的几个基本概念、区域与若尔当曲线。 3.理解复平面点集的几个基本概念;掌握区域、单连通区域和多连通区 域,简单曲线等概念;理解约当曲线的概念并了解约当定理。 第三节 1.复变函数。 2.复变函数的概念、复变函数的极限与连续。 3. 理解复变函数极限的概念,掌握极限等价的刻画定理 1.2;理解复变 函数连续性的概念,掌握连续性等价的刻画定理 1.3;理解有界闭集 上连续函数的三个性质。 第四节 1. 复球面与无穷远点。 2. 复球面、扩充复平面上的几个概念。 3. 了解无穷远点以及扩充复平面的概念 (三)思考与实践 1.思考:复变函数的极限与连续性与实空间中函数极限、连续性的相同 点、不同点。 2.实践:复数、复平面、复变函数的运用,具体问题的求解。 (四)教学方法与手段 本章教学主要采用课堂讲授、多媒体教学、课堂讨论。 第二章 解析函数 (一)目的与要求

1.简单了解数学家柯西勤奋多产、黎曼短暂辉煌的学术人生。让我们知 道并去努力学习伟大学者不但有天分更重要的是对数学事业的热爱和 一生的勤奋坚持、努力:学习他们青年时代就有勇气有魄力挑战学术 前沿难题,推动数学发展,留下人生遗产 2.理解复变函数的导数与微分以及解析函数的概念。 3.掌握连续、可导、解析之间的关系以及求导方法。 4.灵活运用柯西-黎曼条件。 5.理解指数函数、三角函数、双曲函数、根式函数、对数函数、一般幂 函数、一般指数函数以及反三角函数的定义,了解它们的主要性质。 (二)教学内容 第一节 1.解析函数的概念与柯西-黎曼方程。 2.复变函数的导数与微分、解析函数及其简单性质、柯西-黎曼方程。 3.了解数学家柯西将一生奉献于数学事业:数学家黎曼年轻有为,有勇 气有魄力解决学术前沿难题。 4.理解复变函数的导数与微分以及解析函数的概念;掌握连续、可导、 解析之间的关系以及求导方法。 第二节 1.初等解析函数 2.指数函数、三角函数与双曲函数。 3.理解指数函数、三角函数与双曲函数的概念:掌握指数函数、三角函 数的主要性质。 第三节 1.初等多值函数。 2.根式函数、对数函数、一般幂函数与一般指数函数、具有多个有限支 点的情形、反三角函数与反双曲函数。 3.掌握分出根式函数、对数函数的解析分支的方法:理解一般幂函数、 一般指数函数以及反三角函数的定义。 (三)思考与实践 1.思考:复变函数可导与解析的充要调价、充分条件、必要条件是什么? 2.实践:初等函数的求导、复合函数的求导。 (四)教学方法与手段 本章教学主要采用课堂讲授、多媒体教学、课堂讨论。 第三章复变函数的积分 (一)目的与要求
4 1. 简单了解数学家柯西勤奋多产、黎曼短暂辉煌的学术人生。让我们知 道并去努力学习伟大学者不但有天分更重要的是对数学事业的热爱和 一生的勤奋坚持、努力;学习他们青年时代就有勇气有魄力挑战学术 前沿难题,推动数学发展,留下人生遗产。 2. 理解复变函数的导数与微分以及解析函数的概念。 3. 掌握连续、可导、解析之间的关系以及求导方法。 4. 灵活运用柯西-黎曼条件。 5. 理解指数函数、三角函数、双曲函数、根式函数、对数函数、一般幂 函数、一般指数函数以及反三角函数的定义,了解它们的主要性质。 (二)教学内容 第一节 1.解析函数的概念与柯西-黎曼方程。 2.复变函数的导数与微分、解析函数及其简单性质、柯西-黎曼方程。 3.了解数学家柯西将一生奉献于数学事业;数学家黎曼年轻有为,有勇 气有魄力解决学术前沿难题。 4.理解复变函数的导数与微分以及解析函数的概念;掌握连续、可导、 解析之间的关系以及求导方法。 第二节 1.初等解析函数。 2.指数函数、三角函数与双曲函数。 3.理解指数函数、三角函数与双曲函数的概念;掌握指数函数、三角函 数的主要性质。 第三节 1.初等多值函数。 2.根式函数、对数函数、一般幂函数与一般指数函数、具有多个有限支 点的情形、反三角函数与反双曲函数。 3.掌握分出根式函数、对数函数的解析分支的方法;理解一般幂函数、 一般指数函数以及反三角函数的定义。 (三)思考与实践 1.思考:复变函数可导与解析的充要调价、充分条件、必要条件是什么? 2.实践:初等函数的求导、复合函数的求导。 (四)教学方法与手段 本章教学主要采用课堂讲授、多媒体教学、课堂讨论。 第三章 复变函数的积分 (一) 目的与要求

1.了解国内学者王见定教授首次提出半解析函数,共轭解析函数理论, 并发展成双解析函数,复调和函数等新的系统理论。 2.理解复积分的概念及其简单性质,掌握复积分计算的一般方法。 3. 掌握柯西积分定理 4.灵活运用复周线的柯西积分定理。 5.灵活运用柯西积分公式与高阶导数公式。 6.理解解析函数的平均值定理与解析函数的几个等价定理。 7.理解调和函数和共轭调和函数的概念。 8。堂据解析函数与调和函数的关系,堂据共矩调和函数的求法 (二)教学内容 第一节 1.复积分的概念及其简单性质。 2.复变函数积分的定义、复变函数积分的计算问题、复变函数积分的基 本性质。 3.理解复积分的概念及其简单性质、掌握复积分计算的一般方法(参数 法)。 第二节 1.柯西积分定理。 2.柯西积分定理、柯西积分定理得古莎证明、不定积分、柯西积分定理 的推广、柯西积分定理推广到复周线的情形。 3.理解不定积分与原函数的概念,掌握牛顿-莱布尼茨公式 第三节 1.柯西积分公式及其推论。 2.柯西积分公式、解析函数的无穷可微性、柯西不等式与刘维尔定理、 摩勒拉定理、柯西型积分。 3.了解老一辈国内学者王见定教授在世界上首次提出半解析函数理论, 首次提出并系统建立了共轭解析函数理论等,在复变函数领域做了大 范围的原创工作。 4.掌握柯西不等式、刘维尔定理和摩勒拉定理及解析函数的又一个等价 刻画。 第四节 1,解析函数与调和函数的关系 2.拉普拉斯算子、调和函数、共扼调和函数。 3。掌握解析函数与调和函数的关系、掌握共轭调和函数的求法 (三)思考与实践
5 1. 了解国内学者王见定教授首次提出半解析函数,共轭解析函数理论, 并发展成双解析函数,复调和函数等新的系统理论。 2. 理解复积分的概念及其简单性质,掌握复积分计算的一般方法。 3. 掌握柯西积分定理。 4. 灵活运用复周线的柯西积分定理。 5. 灵活运用柯西积分公式与高阶导数公式。 6. 理解解析函数的平均值定理与解析函数的几个等价定理。 7. 理解调和函数和共轭调和函数的概念。 8. 掌握解析函数与调和函数的关系,掌握共轭调和函数的求法。 (二) 教学内容 第一节 1.复积分的概念及其简单性质。 2.复变函数积分的定义、复变函数积分的计算问题、复变函数积分的基 本性质。 3.理解复积分的概念及其简单性质、掌握复积分计算的一般方法(参数 法)。 第二节 1.柯西积分定理。 2.柯西积分定理、柯西积分定理得古莎证明、不定积分、柯西积分定理 的推广、柯西积分定理推广到复周线的情形。 3.理解不定积分与原函数的概念,掌握牛顿-莱布尼茨公式。 第三节 1.柯西积分公式及其推论。 2.柯西积分公式、解析函数的无穷可微性、柯西不等式与刘维尔定理、 摩勒拉定理、柯西型积分。 3.了解老一辈国内学者王见定教授在世界上首次提出半解析函数理论, 首次提出并系统建立了共轭解析函数理论等,在复变函数领域做了大 范围的原创工作。 4.掌握柯西不等式、刘维尔定理和摩勒拉定理及解析函数的又一个等价 刻画。 第四节 1.解析函数与调和函数的关系。 2.拉普拉斯算子、调和函数、共轭调和函数。 3.掌握解析函数与调和函数的关系、掌握共轭调和函数的求法。 (三) 思考与实践

1.思考:复变函数积分的性质、特点。 2.实践:复变函数是否可积分的判定与复积分的求解计算 (四)教学方法与手段 本章教学主要采用课堂讲授、多媒体教学、课堂讨论 第四章解析函数的幂级数表示法 (一) 目的与要求 1.理解复数项级数收敛、发散、绝对收敛与条件收敛的概念与性质。 2.掌握复函数项级数收敛与绝对收敛的充分必要条件。 3.理解幂级数的概念,掌握幂级数收敛半径的求法。 掌握把一些解析函数展开成泰勒级数的方法。 5.掌握解析函数零点的孤立性以及具有零点的解析函数的表达式。 6。理解解析函数零点的孤立性及内部唯一性定理。 7.理解解析函数的最大模原理。 (二)教学内容 第一节 1.复级数的基本性质。 2.复数项级数、一致收敛的复函数项级数、解析函数项级数 3.理解复数项级数收敛、发散、和的概念,并学握收敛性的刻画:掌握 柯西一致收敛准则和优级数准则:掌握复函数项级数的性质,了解复 函数项级数的内闭一致收敛性。 第二 1.幂级数。 2.幂级数的敛散性、收敛半径R的求法、柯西-阿达马公式、幂级数和的 解析性。 3.掌握幂级数的敛散性:理解幂级数的收敛半径,了解收敛圆及收敛圆 周的意义:掌握幂级数和函数的解析性。 第三节 1.解析函数的泰勒展式。 2.泰勒定理、幂级数的和函数在其收敛圆周上的状况、一些初等函数的 泰勤展式。 3.掌握泰勒定理、泰勒系数公式及解析函数的又一等价刻画定理:掌握 把一些解析函数展开成泰勒级数。 第四节 1.解析函数零点的孤立性及唯一性定理。 2.解析函数零点的孤立性、唯一性定理、最大模原理。 6
6 1.思考:复变函数积分的性质、特点。 2.实践:复变函数是否可积分的判定与复积分的求解计算。 (四) 教学方法与手段 本章教学主要采用课堂讲授、多媒体教学、课堂讨论。 第四章 解析函数的幂级数表示法 (一) 目的与要求 1. 理解复数项级数收敛、发散、绝对收敛与条件收敛的概念与性质。 2. 掌握复函数项级数收敛与绝对收敛的充分必要条件。 3. 理解幂级数的概念,掌握幂级数收敛半径的求法。 4. 掌握把一些解析函数展开成泰勒级数的方法。 5. 掌握解析函数零点的孤立性以及具有零点的解析函数的表达式。 6. 理解解析函数零点的孤立性及内部唯一性定理。 7. 理解解析函数的最大模原理。 (二) 教学内容 第一节 1.复级数的基本性质。 2.复数项级数、一致收敛的复函数项级数、解析函数项级数。 3.理解复数项级数收敛、发散、和的概念,并掌握收敛性的刻画;掌握 柯西一致收敛准则和优级数准则;掌握复函数项级数的性质,了解复 函数项级数的内闭一致收敛性。 第二节 1.幂级数。 2.幂级数的敛散性、收敛半径 R 的求法、柯西-阿达马公式、幂级数和的 解析性。 3.掌握幂级数的敛散性;理解幂级数的收敛半径,了解收敛圆及收敛圆 周的意义;掌握幂级数和函数的解析性。 第三节 1.解析函数的泰勒展式。 2.泰勒定理、幂级数的和函数在其收敛圆周上的状况、一些初等函数的 泰勒展式。 3.掌握泰勒定理、泰勒系数公式及解析函数的又一等价刻画定理;掌握 把一些解析函数展开成泰勒级数。 第四节 1.解析函数零点的孤立性及唯一性定理。 2.解析函数零点的孤立性、唯一性定理、最大模原理
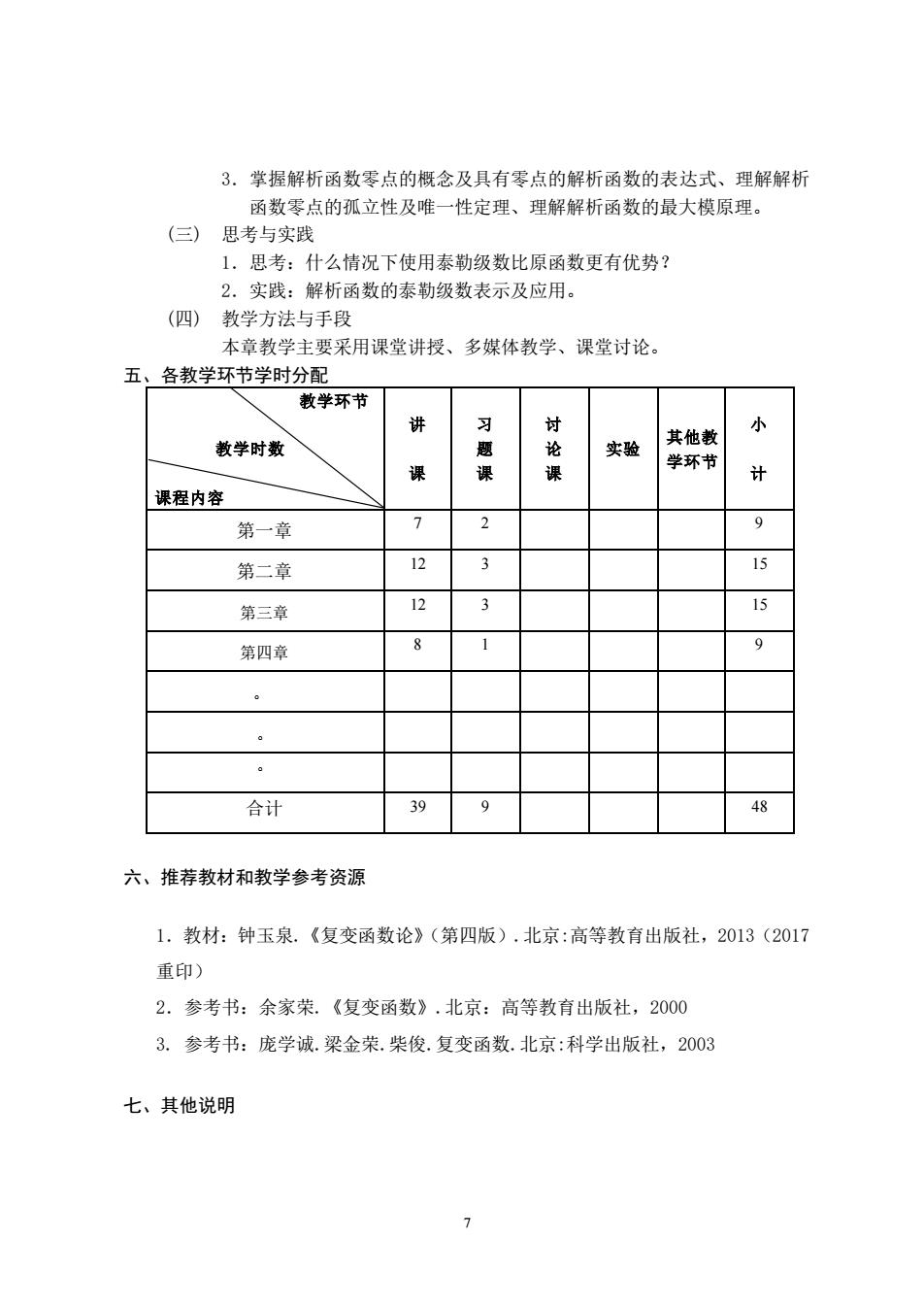
3.掌握解析函数零点的概念及具有秀点的解析函数的表达式、理解解析 函数零点的孤立性及唯一性定理、理解解析函数的最大模原理。 (三)思考与实践 1.思考:什么情况下使用泰勒级数比原函数更有优势? 2.实践:解析函数的泰勒级数表示及应用。 (四)教学方法与手段 本章教学主要采用课堂讲授、多媒体教学、课堂讨论。 五、各教学环节学时分配 学环节 讨 小 其他刺 教学时数 题课 实验 课 学环书 计 课程内容 第一章 7 9 第二章 2 3 15 第三章 12 3 15 第四章 1 9 。 合计 48 六、推荐教材和教学参考资源 1.教材:钟玉泉.《复变函数论》(第四版).北京:高等教育出版社,2013(2017 重印 2.参考书:余家荣.《复变函数》.北京:高等教育出版社,2000 3.参考书:庞学诚.梁金荣.柴俊.复变函数.北京:科学出版社,2003 七、其他说明 7
7 3.掌握解析函数零点的概念及具有零点的解析函数的表达式、理解解析 函数零点的孤立性及唯一性定理、理解解析函数的最大模原理。 (三) 思考与实践 1.思考:什么情况下使用泰勒级数比原函数更有优势? 2.实践:解析函数的泰勒级数表示及应用。 (四) 教学方法与手段 本章教学主要采用课堂讲授、多媒体教学、课堂讨论。 五、各教学环节学时分配 教学环节 教学时数 课程内容 讲 课 习 题 课 讨 论 课 实验 其他教 学环节 小 计 第一章 7 2 9 第二章 12 3 15 第三章 12 3 15 第四章 8 1 9 。 。 。 合计 39 9 48 六、推荐教材和教学参考资源 1.教材:钟玉泉.《复变函数论》(第四版).北京:高等教育出版社,2013(2017 重印) 2.参考书:余家荣.《复变函数》.北京:高等教育出版社,2000 3. 参考书:庞学诚.梁金荣.柴俊.复变函数.北京:科学出版社,2003 七、其他说明

大纲修订人:张登朋 修订日期:2020.12 大纲审定人: 审定日期:
8 大纲修订人:张登朋 修订日期:2020.12 大纲审定人: 审定日期: