
《近世代数》课程教学大纲 一、课程基本信息 课程代码:18100273 课程名称:近世代数 英文名称:Modem Algebra 课程类别:专业课 时:32 学分:2 适用对象:数学与应用数学专业 考核方式:考试 先修课程:高等代数 二、课程简介 中文简介 近世代数主要内容为抽象代数,其中研究各种代数结构,也就是具有代数运算的集合,以及 在这些结构中保持运算的映射(称为态射)。抽象代数为现代数学、现代物理学、现代化学、计算 机科学、信息科学以及密码学等提供了语言、思想与研究方法。在信息时代,析世代数的应用日 趋广泛。本课程将主要介绍近世代数的重要结构如群、环和域等的相关概念与基础理论。 英文简介 The main content of modern algebra is abstract algebra.in which various algebraic structures.ie. sets with algebraic operations,and the mappings(called morphisms)that maintain operations in these structures,are studied.Abstract algebra provides language,ideas and research methods for modern mathematics modern physics,modemn chemistry,computer scienc information science,and cryptography.In the information era the application of modern algebra has become increasingly widespread.This will mainly introduce the related conepts and basic theories of importan algebraic structures of modern algebra such as groups,rings and fields. 三、课程性质与教学目的 近世代数是介绍以群、环和域为代表的代数结构,代数结构之间的态射,结构的分析构造及 其应用等的一门学科。是数学与应用数学专业选修课。 通过本课程的教学,应使得学生了解近世代数的发展历史、主要研究对象以及其应用。理解 重要的几类代数结构的相关概念和理论,掌握基础的代数结构分析、分解和性质证明的思想方法, 尤其是态射的运用,提高学生的数学修养和数学技巧,培养学生的数学成熟度。同时,了解我国 古代的相关成就,如中国剩余定理,以及近代数学家对代数结构的研究和代数结构在各学科的应
1 《近世代数》课程教学大纲 一、课程基本信息 课程代码:18100273 课程名称:近世代数 英文名称:Modern Algebra 课程类别:专业课 学 时:32 学 分:2 适用对象:数学与应用数学专业 考核方式:考试 先修课程:高等代数 二、课程简介 中文简介 近世代数主要内容为抽象代数,其中研究各种代数结构,也就是具有代数运算的集合,以及 在这些结构中保持运算的映射(称为态射)。抽象代数为现代数学、现代物理学、现代化学、计算 机科学、信息科学以及密码学等提供了语言、思想与研究方法。在信息时代,近世代数的应用日 趋广泛。本课程将主要介绍近世代数的重要结构如群、环和域等的相关概念与基础理论。 英文简介 The main content of modern algebra is abstract algebra, in which various algebraic structures, i.e. sets with algebraic operations, and the mappings (called morphisms) that maintain operations in these structures, are studied. Abstract algebra provides language, ideas and research methods for modern mathematics, modern physics, modern chemistry, computer science, information science, and cryptography. In the information era, the application of modern algebra has become increasingly widespread. This course will mainly introduce the related concepts and basic theories of important algebraic structures of modern algebra such as groups, rings and fields. 三、课程性质与教学目的 近世代数是介绍以群、环和域为代表的代数结构,代数结构之间的态射,结构的分析构造及 其应用等的一门学科。是数学与应用数学专业选修课。 通过本课程的教学,应使得学生了解近世代数的发展历史、主要研究对象以及其应用。理解 重要的几类代数结构的相关概念和理论,掌握基础的代数结构分析、分解和性质证明的思想方法, 尤其是态射的运用,提高学生的数学修养和数学技巧,培养学生的数学成熟度。同时,了解我国 古代的相关成就,如中国剩余定理,以及近代数学家对代数结构的研究和代数结构在各学科的应

用所作出的贡献。 四、教学内容及要求 第一模块引言 (一)目的与要求 1.了解近世代数的发展历史 2.了解几类代数结构的基本概念 3.了解代数结构的应用 (二)教学内容 第一节 1.主要内容:群、环、域的概念介绍,群、环、域的实例,群论的应用。 2.基本概念和知识点:代数结构、群、环、域、态射。 3.问题与应用(能力要求):了解理论和应用中可以用代数结构来建模和 求解的众多问题。 (三)思老与实践 调查了解代数在国民生产和日常生活中的应用。思政内容:我国代数学家 王小云转攻密码学后设计了MD5碰撞算法(但不是破解)。 (四)教学方法与手段 本章教学主要采用的方法和手段包括课堂讲授、多媒体教学、网络辅助教 学和课堂讨论。 第二模块群 (一)目的与要求 1.了解群论发展历史及其意义 2.掌握群论中重要的基本概念 3.理解群论的同构和同态定理、Sylow定理 4.理解群在集合上的作用 (二)教学内容 1.主要内容: (1)群的概念、群的实例、对称群和置换群;(2)子群、陪集、Lagrange 定理:(3)群的同构与直积:(4)群同态、正规子群、商群和可解群:(⑤) 群在集合上的作用:(6)Sv1ow定理:(7)有限Abe1群的结构。 2.基本概念和知识点: 群、n元对称群、置换群、子群、陪集、指数、Lagrange定理、同构 映射、群的直积、群同态、同态的核、正规子群、商群、群同态基本 2
2 用所作出的贡献。 四、教学内容及要求 第一模块 引言 (一)目的与要求 1.了解近世代数的发展历史 2.了解几类代数结构的基本概念 3.了解代数结构的应用 (二)教学内容 第一节 1.主要内容:群、环、域的概念介绍,群、环、域的实例,群论的应用。 2.基本概念和知识点:代数结构、群、环、域、态射。 3.问题与应用(能力要求):了解理论和应用中可以用代数结构来建模和 求解的众多问题。 (三)思考与实践 调查了解代数在国民生产和日常生活中的应用。思政内容:我国代数学家 王小云转攻密码学后设计了 MD5 碰撞算法(但不是破解)。 (四)教学方法与手段 本章教学主要采用的方法和手段包括课堂讲授、多媒体教学、网络辅助教 学和课堂讨论。 第二模块 群 (一)目的与要求 1.了解群论发展历史及其意义 2.掌握群论中重要的基本概念 3.理解群论的同构和同态定理、Sylow 定理 4.理解群在集合上的作用 (二)教学内容 1.主要内容: (1)群的概念、群的实例、对称群和置换群; (2)子群、陪集、Lagrange 定理; (3)群的同构与直积; (4)群同态、正规子群、商群和可解群; (5) 群在集合上的作用; (6) Sylow 定理; (7)有限 Abel 群的结构。 2.基本概念和知识点: 群、n 元对称群、置换群、子群、陪集、指数、Lagrange 定理、同构 映射、群的直积、群同态、同态的核、正规子群、商群、群同态基本

定理、第一同构定理、第二同构定理、单群、可解群、群在集合上的 作用、群自同构、轨道、轨道-稳定子定理、Sylow定理、有限Abe】 群的分解。 3.问题与应用(能力要求): 能够使用若干基本定理进行群结构分析工作,如懂得分析循环群、有 限Abl群、阶数较小的群的结构。懂得运用群在集合上的作用进行组 合计数 (三)思考与实践 可以确定阶数较小的群的结构作为一个小项目去完成。思政内容:中国数 学在“最长的数学证明”有限单群分类问题中的贡献。 (四)教学方法与手段 本章教学主要采用的方法和手段包括课堂讲授、多媒体教学、网络辅助教 学、团队合作和课堂讨论。 第三模块环 (一)目的与要求 1.理解环论的相关概念 2.理解环的同态、同构定理 3.掌握环和域的构造 (二)教学内容 1.主要内容: ()环、整环、交换环、除环、域的概念及若干实例;(②)理想、商环、 陪集的概念,环同态与核,同余和中国剩余定理:(③)素理想、极大 理想、有限域的构造:(4)代数数域和Galois环的构造. 2.基本概念和知识点: 环、整环、交换环、除环、域、理想、商环、陪集、环同态、核、素 理想、极大理想、代数数、超越数、代数数域、Galois环. 3.问题与应用(能力要求): 懂得构造指定大小的有限域, (三)思考与实践 了解5次以上方程求解问题的研究历史。思政内容:由中国剩余定理看古 代中国数学成就。 (四)教学方法与手段 本章教学主要采用的方法和手段,如课堂讲授、多媒体教学、网络辅助教 学、团队合作和课堂讨论等。 3
3 定理、第一同构定理、第二同构定理、单群、可解群、群在集合上的 作用、群自同构、轨道、轨道-稳定子定理、Sylow 定理、有限 Abel 群的分解。 3.问题与应用(能力要求): 能够使用若干基本定理进行群结构分析工作,如懂得分析循环群、有 限 Abel 群、阶数较小的群的结构。懂得运用群在集合上的作用进行组 合计数。 (三)思考与实践 可以确定阶数较小的群的结构作为一个小项目去完成。思政内容:中国数 学在“最长的数学证明”有限单群分类问题中的贡献。 (四)教学方法与手段 本章教学主要采用的方法和手段包括课堂讲授、多媒体教学、网络辅助教 学、团队合作和课堂讨论。 第三模块 环 (一)目的与要求 1.理解环论的相关概念 2.理解环的同态、同构定理 3.掌握环和域的构造 (二)教学内容 1.主要内容: (1)环、整环、交换环、除环、域的概念及若干实例; (2)理想、商环、 陪集的概念,环同态与核,同余和中国剩余定理; (3) 素理想、极大 理想、有限域的构造; (4) 代数数域和 Galois 环的构造. 2.基本概念和知识点: 环、整环、交换环、除环、域、理想、商环、陪集、环同态、核、素 理想、极大理想、代数数、超越数、代数数域、Galois 环. 3.问题与应用(能力要求): 懂得构造指定大小的有限域. (三)思考与实践 了解 5 次以上方程求解问题的研究历史。思政内容:由中国剩余定理看古 代中国数学成就。 (四)教学方法与手段 本章教学主要采用的方法和手段,如课堂讲授、多媒体教学、网络辅助教 学、团队合作和课堂讨论等

第四模块域扩张 (一)目的与要求 1.理解域扩张等理论 2.掌握Galois扩张和Galois基本定理 3.理解Galois理论及其关于代数方程可解性的工作 (二)教学内容 1,主要内容: (1)域扩张、分裂域、正规扩张、可分扩张:(2)域扩张的自同构群、 Galois扩张、Galois基本定理 2.基本概念和知识点: 分裂域、正规扩张、可分扩张、Galois扩张、Galois基本定理、 Abel-Ruffini定理 3.问题与应用(能力要求): 理解Galois理论的证明,即5次以上方程的可解性问题的解答. (三)思考与实践 思政内容:华罗庚成名作《苏家驹之代数的五次方程式解法不能成立之理 由》的启迪意义。 (四)教学方法与手段 本章教学主要采用的方法和手段,如课堂讲授、多媒体教学、网络辅助教 学、团队合作和课堂讨论等。 4
4 第四模块 域扩张 (一)目的与要求 1.理解域扩张等理论 2.掌握 Galois 扩张和 Galois 基本定理 3.理解 Galois 理论及其关于代数方程可解性的工作 (二)教学内容 1.主要内容: (1) 域扩张、分裂域、正规扩张、可分扩张; (2) 域扩张的自同构群、 Galois 扩张、Galois 基本定理 2.基本概念和知识点: 分裂域、正规扩张、可分扩张、Galois 扩张、Galois 基本定理、 Abel-Ruffini 定理 3.问题与应用(能力要求): 理解 Galois 理论的证明,即 5 次以上方程的可解性问题的解答. (三)思考与实践 思政内容:华罗庚成名作《苏家驹之代数的五次方程式解法不能成立之理 由》的启迪意义。 (四)教学方法与手段 本章教学主要采用的方法和手段,如课堂讲授、多媒体教学、网络辅助教 学、团队合作和课堂讨论等
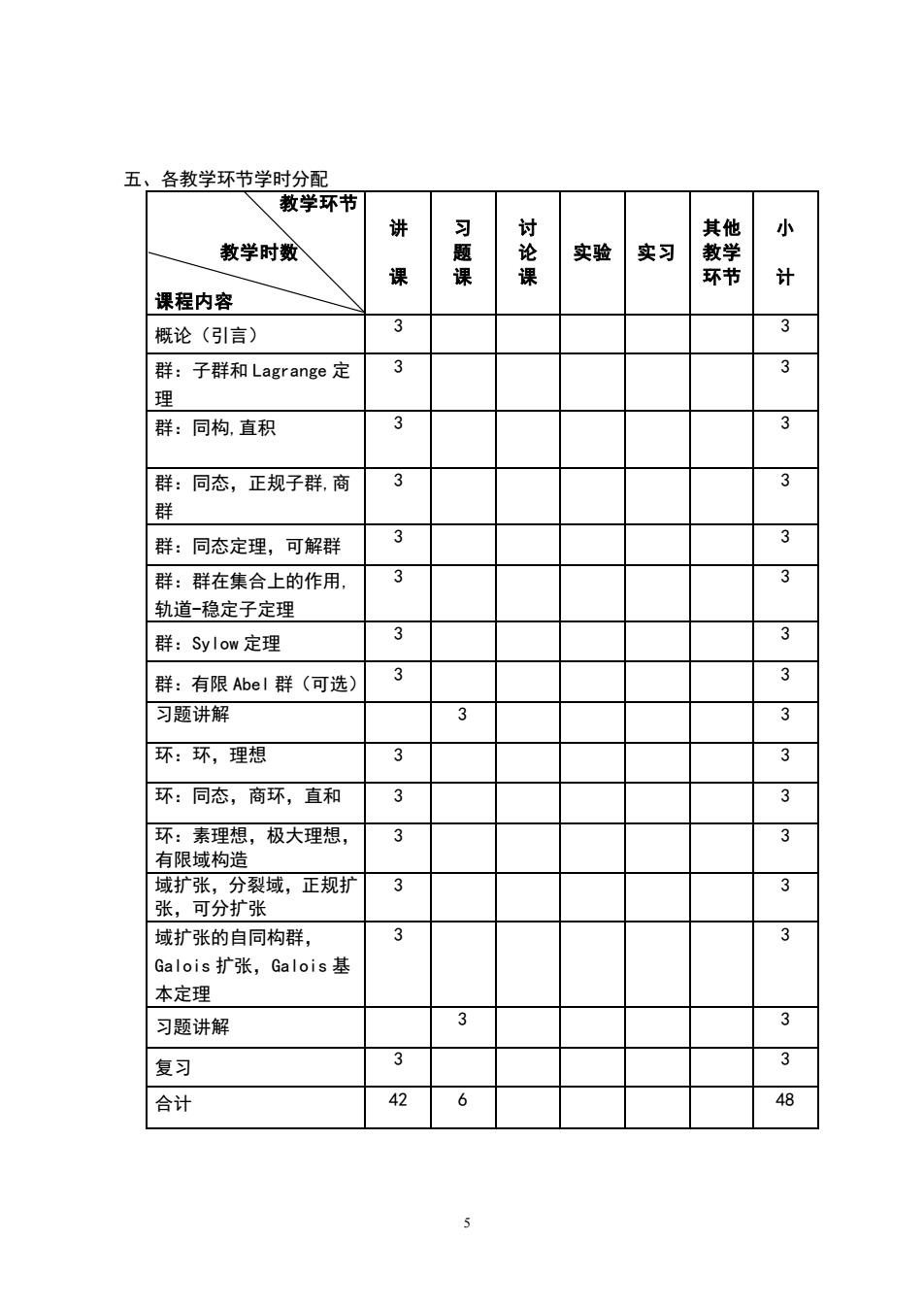
五、各教学环节学时分配 教学环节 讲 其他 小 教学时数 罩 谁 实验实习 课 环节 计 课程内容 概论(引言) 3 群:子群和Lagrange定 理 群:同构,直积 33 群:同态,正规子群商 群 群:同态定理,可解群 3 群:群在集合上的作用, 轨道-稳定子定理 群:Sylow定理 3 3 群:有限Abel群(可选) 3 习题讲解 3 3 环:环,理想 3 环:同态,商环,直和 3 环:素理想,极大理想, 3 3 有限域构造 域扩张,分裂域,正规打 3 3 张,可分扩张 域扩张的自同构群, 3 3 Galois扩张,Galois基 本定理 习题讲解 3 3 复习 3 合计 48 5
5 五、各教学环节学时分配 教学环节 教学时数 课程内容 讲 课 习 题 课 讨 论 课 实验 实习 其他 教学 环节 小 计 概论(引言) 3 3 群:子群和 Lagrange 定 理 3 3 群:同构,直积 3 3 群:同态,正规子群,商 群 3 3 群:同态定理,可解群 3 3 群:群在集合上的作用, 轨道-稳定子定理 3 3 群:Sylow 定理 3 3 群:有限 Abel 群(可选) 3 3 习题讲解 3 3 环:环,理想 3 3 环:同态,商环,直和 3 3 环:素理想,极大理想, 有限域构造 3 3 域扩张,分裂域,正规扩 张,可分扩张 3 3 域扩张的自同构群, Galois 扩张,Galois 基 本定理 3 3 习题讲解 3 3 复习 3 3 合计 42 6 48

六、课程考核 (一)考核方式:考试 (二)成绩构成 平时成绩占比:50%期末考试占比:50% (三)成绩考核标准 课堂考勤:准时到达课堂,不迟到,不早退,占10%;课堂表现:遵守课堂秩序, 认真听讲,积极参与课堂互动,占10%;平时作业:按时,高质量完成平时作业,占%30; 期末考试:占50%。 七、推荐教材和教学参考资源 1.丘维声.抽象代数基础。高等教有出版社,2015. 2.丘维声.近世代数.北京大学出版社,2015. 3.刘绍学,章璞.近世代数导.高等教育出版社,2011. 4.Lederman.Introduction to Group Theory.Oliver and Boyd,1973. 5.膜沛,邓少强.简明抽象代数.高等教有出版社,2003. 6。Carter著,郭小强,罗翠玲译.群论彩图版.机械工业出版社,2019 7.Jacobson.Basic Algebra I,II.Dover,1985. 8.Artin.Algebra.Pearson College Div,1991. 八、其他说明 无 大纲修订人:张赞波 修订日期:2020.12 大纲审定人: 审定日期: 6
6 六、课程考核 (一)考核方式:考试 (二)成绩构成 平时成绩占比:50% 期末考试占比:50% (三)成绩考核标准 课堂考勤:准时到达课堂,不迟到,不早退,占 10%;课堂表现:遵守课堂秩序, 认真听讲,积极参与课堂互动,占 10%;平时作业:按时,高质量完成平时作业,占%30; 期末考试:占 50%。 七、推荐教材和教学参考资源 1. 丘维声. 抽象代数基础. 高等教育出版社, 2015. 2. 丘维声. 近世代数. 北京大学出版社, 2015. 3. 刘绍学, 章璞. 近世代数导引. 高等教育出版社, 2011. 4. Lederman. Introduction to Group Theory. Oliver and Boyd, 1973. 5. 顾沛, 邓少强. 简明抽象代数. 高等教育出版社, 2003. 6. Carter 著, 郭小强, 罗翠玲译. 群论彩图版. 机械工业出版社, 2019. 7. Jacobson. Basic Algebra I, II. Dover, 1985. 8. Artin. Algebra. Pearson College Div, 1991. 八、其他说明 无 大纲修订人:张赞波 修订日期:2020.12 大纲审定人: 审定日期: