
商知京大竖 NANJING UNIVERSITY 第6章赋权图 第7章有向图 程龚 2023/4/10
第6章 赋权图 第7章 有向图 程龚 2023/4/10 1
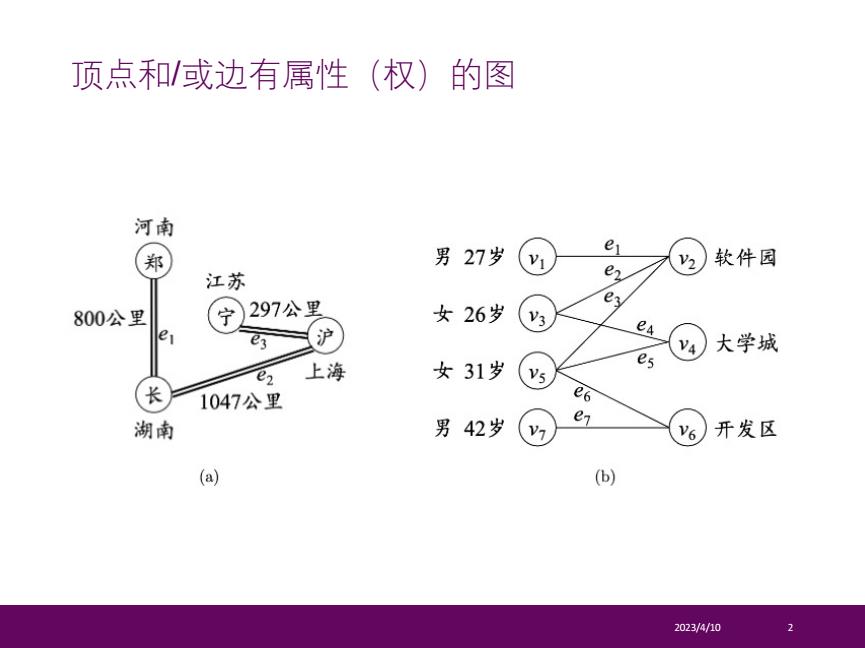
顶点和/或边有属性(权) 的图 河南 郑 男27岁 el 软件园 江苏 e 2 800公里 宁 297公里 女26岁 V3 e es 沪 ex 大学城 上海 女31岁 es e 长 1047公里 e6 湖南 男42岁 e V6 开发区 (a) (b) 2023/4/10
2023/4/10 2 顶点和/或边有属性(权)的图

边有方向(和权) 的图 限4人 a e es a 05 限3人 a as 限4人 e a6 V4 V2 a3/ as a4 限3人 4限4 限3人4 e a v3 V3 限5人 2023/4/10 3
2023/4/10 3 边有方向(和权)的图

本次课的主要内容 6.1赋权图和距离 6.2最小生成树 6.3赋权欧拉图 6.4赋权哈密尔顿图 7.1有向图的定义 72有向图的表示 7.3有向图的连通 7.4有向图的距离 7.5流网络和最大流 2023/4/10
6.1 赋权图和距离 6.2 最小生成树 6.3 赋权欧拉图 6.4 赋权哈密尔顿图 7.1 有向图的定义 7.2 有向图的表示 7.3 有向图的连通 7.4 有向图的距离 7.5 流网络和最大流 2023/4/10 4 本次课的主要内容

本次课的主要内容 6.1赋权图和距离 6.2最小生成树 6.3赋权欧拉图 6.4赋权哈密尔顿图 7.1有向图的定义 7.2有向图的表示 7.3有向图的连通 7.4有向图的距离 7.5流网络和最大流 2023/4/10
6.1 赋权图和距离 6.2 最小生成树 6.3 赋权欧拉图 6.4 赋权哈密尔顿图 7.1 有向图的定义 7.2 有向图的表示 7.3 有向图的连通 7.4 有向图的距离 7.5 流网络和最大流 2023/4/10 5 本次课的主要内容

赋权图和距离 ■赋权图:G= 3 ●V:顶点的有限集合 VS ●E:边的有限集合 ●w:赋权函数,E→ -w(e):边e的权 2023/4/10
n 赋权图:G = l V:顶点的有限集合 l E:边的有限集合 l w:赋权函数, E à R – w(e):边e的权 2023/4/10 6 赋权图和距离
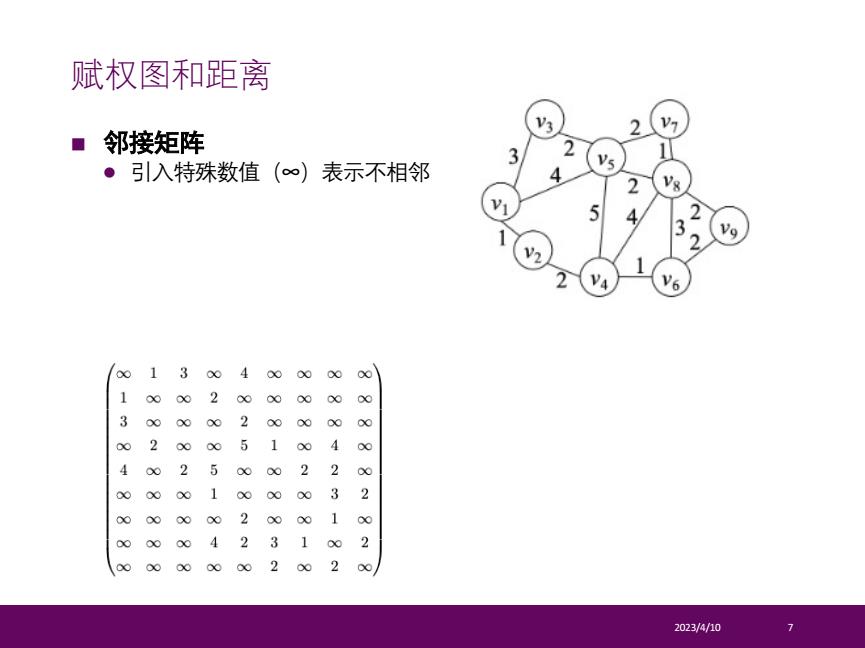
赋权图和距离 ■邻接矩阵 ·引入特殊数值(∞)表示不相邻 3 2 9 V6 013004 0000 1 00 2 0 3 2 2 6 00 1 40∞ 2 00 0 00 0 33 P 1 6 2 3 202 00000 200200 2023/4/10
n 邻接矩阵 l 引入特殊数值(∞)表示不相邻 2023/4/10 7 赋权图和距离
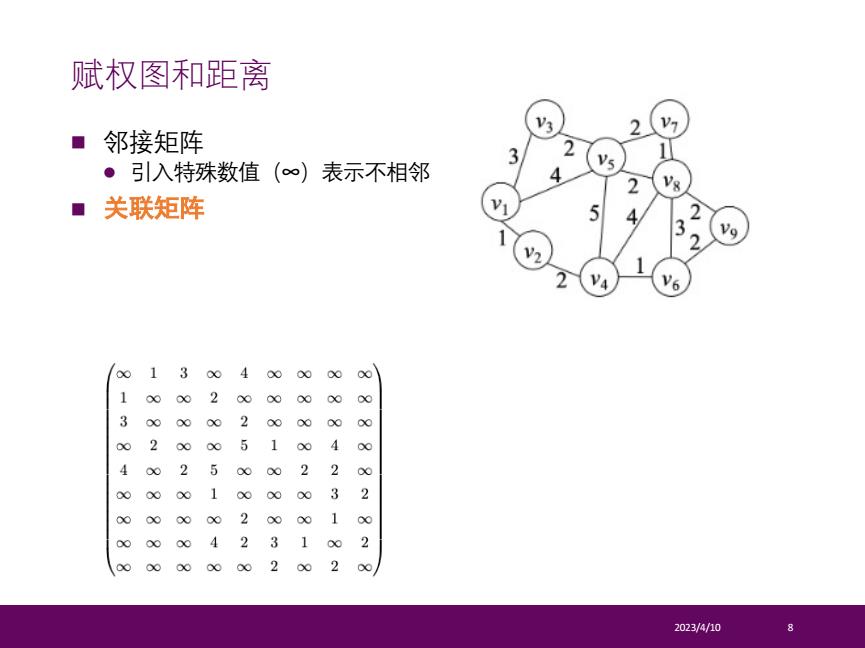
赋权图和距离 ■邻接矩阵 ·引入特殊数值(∞)表示不相邻 ■关联矩阵 13004 0∞ 1 6 200 3 00 2 00 2 00 4 1 4 00 2 P % 0 88 6 6 22 3 1 88 88 8 P 4 1 00 2 00 2023/4/10
n 邻接矩阵 l 引入特殊数值(∞)表示不相邻 n 关联矩阵 2023/4/10 8 赋权图和距离
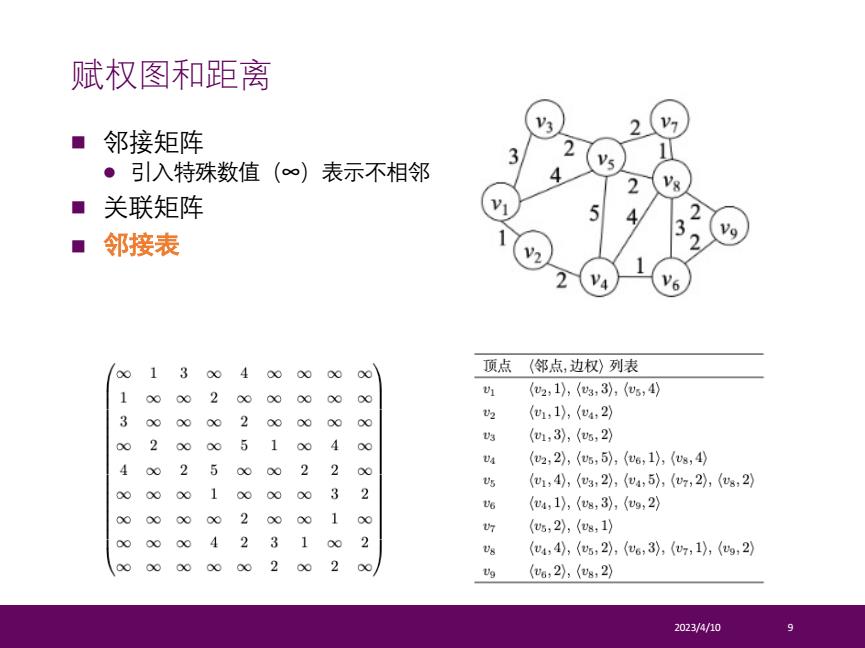
赋权图和距离 ■邻接矩阵 ·引入特殊数值(∞)表示不相邻 ■关联矩阵 ■邻接表 13 004 0000 顶点(邻点,边权)列表 1 2 0 6 00 U (2,1,(g,3),(5,4) 3 的 (1,1,(e4,2) 2 1 88 内 (,3,(6,2) 00 3 (2,2),(5,5),(6,1),(v8,4 00 2 (1,4,(,2),(4,5),(,2,(g,2) b 3 2 (4,1),(g,3),(g,2) 88 6 9 (,2,(8,1) 6 2 3 P 2 g (U4,4,(,2),(6,3),(7,1),(g,2 00 00 2 2 g (6,2,(g,2) 2023/4/10
n 邻接矩阵 l 引入特殊数值(∞)表示不相邻 n 关联矩阵 n 邻接表 2023/4/10 9 赋权图和距离

赋权图和距离 ■(赋权)长度 ● 经过的边的权和 2023/4/10 10
n (赋权)长度 l 经过的边的权和 2023/4/10 10 赋权图和距离