西安电子科技大学：《概率论与数理统计》课程教学资源（课件讲稿）第七章 参数估计（习题课）

2019/12/22 第七 参数估计 一、重点与难点 习题课 1重点 最大似然估计. 一、重点与难点 一个正态总体参数的区间估计 二、主要内容 2.难点 三、典型例愿 显着性水平a与量信区间 ⊙⊙@ 二、主要内容 一.填空题： 1)设总体X-U[0,小，(X,X,X)是来自X的样 本，则的极大拟松估计量是} J月sxs0 6其它 ④⊙0 。非色本起作保酒 2)设总体X-N(4,0.9)容量为9的简单随即变量 即0- 0其它 均未智参数“的I信度为如为的直倍区 解：2=0.9已知， ,0=小 而=5，n=9,a=09.a=L05,5g==1.96 故名发-g信区间为5测） 0⑧0 ④⊙0

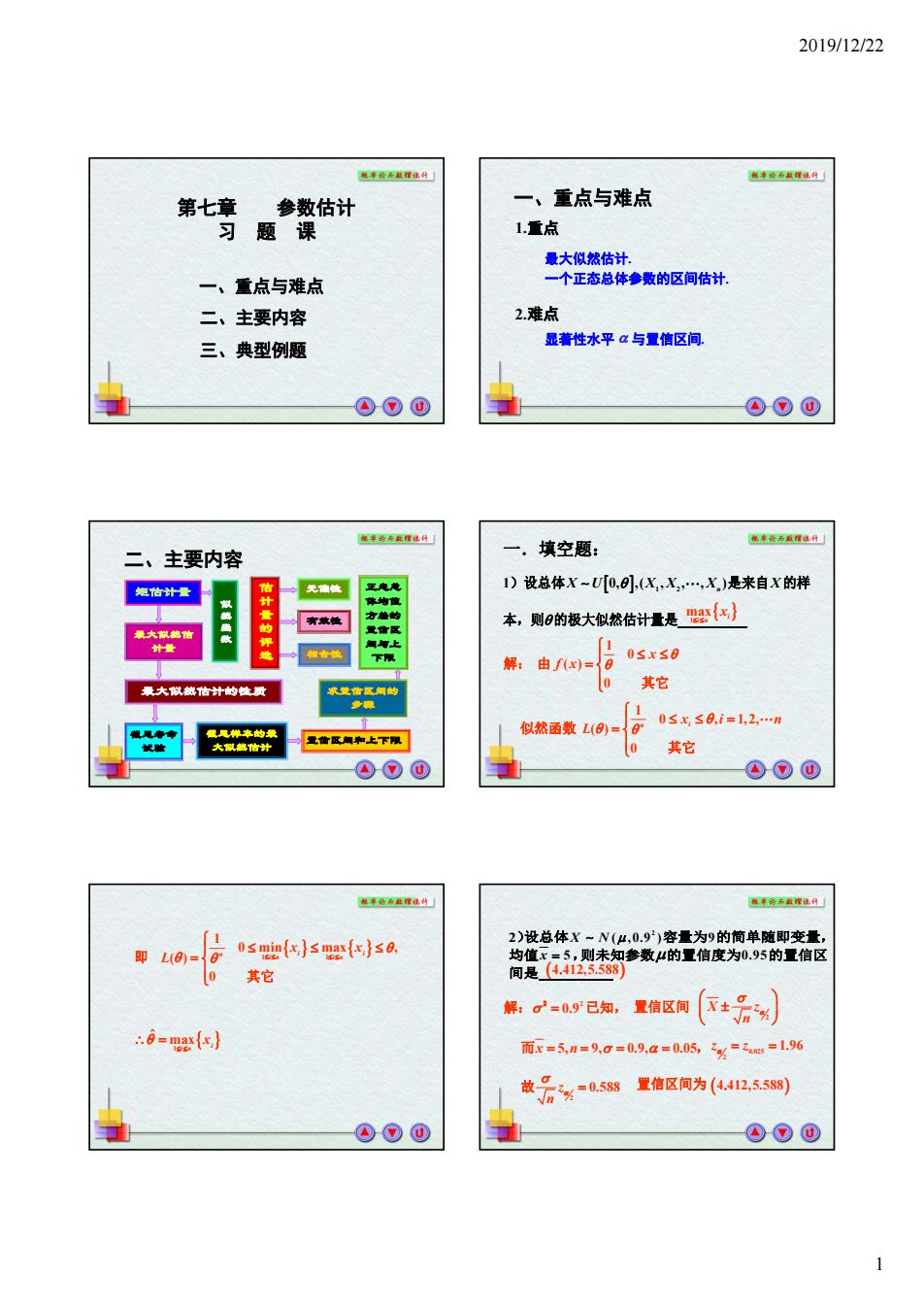
2019/12/22 1 第七章 参数估计 习题课 一、重点与难点 三、典型例题 二、主要内容 一、重点与难点 1.重点 最大似然估计. 一个正态总体参数的区间估计. 2.难点 显著性水平 与置信区间  . 矩估计量 估计量的评选 截尾样本的最 大似然估计 截尾寿命 试验 二、主要内容 最大似然估 计量 最大似然估计的性质 似然函数 无偏性 正态总 体均值 方差的 置信区 间与上 下限 有效性 置信区间和上下限 求置信区间的 步骤 相合性 一．填空题： 1）设总体   1 2 0, ,( , , , ) X U XX X  n   是来自X 的样 本，则 的极大似然估计量是 1 0 ( ) 0 x f x           解： 由 其它 1 0 , 1,2, ( ) 0 n i xi n L             似然函数 其它   1 max i i n x     1 1 1 0 min max , ( ) 0 n i i i n i n x x L              即   其它   1 ˆ max i i n  x     2   0.9 解： 已知， 2 2 X z n          2）设总体 2 X N  ( ,0.9 )  容量为9的简单随即变量， 均值x  5，则未知参数的置信度为0.95的置信区 间是 置信区间 而 ， x n    5, 9, 0.9, 0.05   0.025 2 z z 1.96    2 z 0.588 n   故  置信区间为   4 412,5.588 . 4 412,5.588 . 

2019/12/22 二、选择题： 意来长动来得银用 2的计是自位体X的一个样本，则 2总体X 时 拉是品的向染 心： 81g: 836s4o7e, (D)+ 解：由%=X敬=4=2X 解：重信区间为下±号为依题意，区间长度 面4名-2- 0⊙@ 所以≥-1364 3)设XXX为总体X的一个随机样苯， 三、证明题 E(X)=H,DX)=g,6=C2(X-X)为g的 对一受计其率，质机取 ”若先让求最大似然估计？ 无偏估计，则C= (C) (A)I x-取 解：E()=c(x-x月 试证明p=R= X是P的无偏估计量。 -:)-C(EX-2EXE 正明：X-B1.p,所以EX)=P,EX)=P c2g+r2w）小-2a-icg-g 散E-EG=E艺X小P 因而P是P的无偏估计 ⊙ ©⊙0 四设解答题 为总体X的一个样本的密度菌 数f(x) ,0,>0求参数B的矩告计 和大估 其他 n(()=niB+(B-)2n B 求导教得行+公加0 解E(-x在= :矩估量日。 A=-4 制松函数为 大心速后钠广 4=n-0a.%<u 其他 当当x2n时O00 ④⊙@

2019/12/22 2 1)设 1 2 , ,, X X Xn  是取自总体 X 的一个简单样本，则 2 E( ) X 的矩估计是 （A） 2 2 1 1 1 ( ) 1 n i i S X X n      （B） 2 2 2 1 1 ( ) n i i S X X n     （C） 2 2 S1  X （D） 2 2 S2  X 二、 选择题： 2 解：由2  E( ) X D 2 2 2 1 1 ( ) n i i E XA X n  故    n n i i i i n i i S X XX X X X X n n X n 2 2 22 2 22 2 1 1 2 1 1 1 ( ) 1            而 2）总体 2 X N  (, )   ， 2  已知，n  时， 才能使总体均值 的置信度为0.95的置信区间长不大 于 L （A）15 2  / 2 L ; （B）15.3664 2  / 2 L ; （C）16 2  / 2 L ; （D）16 解： ( ) B 2 X z n          置信区间为 依题意，区间长度   2 2 2 2 2 2 4 n z 15.3664 L L    所以   2 0.05, 1.96 z 而由    2 2 z L n    ( ) C 3）设 1 2 , ,, XX Xn  为总体 X 的一个随机样本， 2 EX DX () ,()     ，  1 2 2 1 1 ( ) n i i i  CX X       为 2  的 无偏估计，则 C＝ （A）1 n （B） 1 n  1 （C）   1 2 1 n  （D） 1 n  2 解：   ˆ 2 E    1 2 1 1 n i i i EC X X                n n i ii i i i C E X X X X C EX EX EX 1 1 2 22 1 1 1 1 2 22                  1 22 2 1 2 2 n i C         2 2   2( 1) n C  1 2( 1) C n    三、证明题 证明：XBp ~ (1, )，所以 E() , X p  ( ) E X p i   故 E() ( ) p EX  1 1 n i i E X n           p  因而 是p p的无偏估计. 为了对一批产品估计其废品率 p ，随机取一 样本 X1, X2 ,…, Xn ,其中 1 0 i i=1,2, ,n , X ,      取得次品 （ ） 取得合格品 试证明 是 p 的无偏估计量 .  1 1 n i i pX X n     若先让求最大似然估计？ (书P239) 四、 解答题 1）设 1 2 , ,, XX Xn  为总体X 的一个样本, X 的密度函 数 1 ,0 1 ( ) 0 , x x f x          其他 ,   0求参数 的矩估计 量和极大似然估计量。 解：   1 0 1 0 1 E X x x dx      1 1       1 1 1     1  ˆ 1 X     矩估量 0 2 似然函数为 1 () () n i i L  f x    1 1 , 0 1, 1,2, 0 , n i i i x xi n               其他 0 1, 1, 2, i 当 时   xi n    1 ln ( ) ln 1 ln n i i Ln x       求导数得 1 ln 0 n i i n x      1 ˆ ln n i i n x      最大似然估计值为 1 ˆ ln n i i n X      最大似然估计量为

2019/12/22 爬丰轮兵融维线研 能本能品盐维证研 2)随机地从一批零件中抽取16个，测得长度(cm) 为：2.14,2.10,2.13,2.15,2.13,2.12,2.13,2.10， 解：(2)σ未知，则置信区间为 ±4- 2.15,2.12,2.14,2.10,2.13,2.11,2.14,2.11,设 零件长度分布为正态分布，试求总体4的90%的置信 而r=2125,n=16,。L004 a=0.10, 区间：(1)若a=0.01(cm),(2)若c未知。 15 解：(1)g=0.01已知置信区间为 'gw-0=1e15)=1.7531 而r=2125n=16,g=0.01,a=0.10,g=乙s=1645 故多-小=购】 g=0.00 故 置信区间为(2.121,2.129) 置信区间为(2.1175,2.1325) ④⊙⑩ ④⊙① 整丰色示款维线件 怎车铃布数像保行 3)设某异常区磁场强度服从正态分布N(4,σ)， 4)某厂利用两条自动化流水线灌装番茄酱，分别以两 现对该区进行磁测，按仪器规定其方差不得超过 条流水线上抽取样本：X,X…X及，Y,Y, 0.01,今抽测16个点，算得x=12.7,s2=0.0025, 算出灭=10.6(g,7=9.5(g),S2=2.4,S2=4.7,假设这两 问此仪器工作是否稳定(a=0.05)? 条流水线上灌装的番茄酱的重量都服从正态分布，且相 互独立，其均值分别为4，，(1)设两总体方差c=σ， 解n=16,a=0.05,X2s15)=27.5, 求4，一4，置信度为5%的置信区间：(2)求σ/σ的置信 2Xs(15)=6.26,σ2的1-a置信区间为 度为95%的置信区间。（书P293,习题16） n-1S2n-1)S 解：()置信区间为 =(0.00136,0.00599), xan(n-1)'Zi-an(n-1)) 11 由于方差σ2不超过0.01，故此仪器工作稳定. x-T±S。 (m+%-2) ④⊙⊙ ⊙⊙ 款单伦务盖作谈饼 解：(2②)置信区间为 卷半伦布点维丝研 其中S。= (m-1)S+(B-1S 1 S (n+u-2) Fgm-1%-SFg4-1%-0 =10.6(g),7=9.5g,S=24,S=4.7 S=2.4S=4.7a=0.05, n=12,m2=17,4+月-2=27，a=0.05 %=12,%2=17,4-1=11,n-1=16, gm+%-2)=1(27刃=2.0518 F,(4-1,%-1)=Fs01,16)=2.94 + 4-14-1)= 1 1 ·x(m+-2)=1501 n,-1,4-1)-r16,1m33 里信区间为（0.401,2.601) 置信区间为(0.1737,1.7004) ①⊙⊙ 区备用制愿面 ④⊙⊙ 3

2019/12/22 3 2）随机地从一批零件中抽取 16 个，测得长度( ) cm 为：2.14，2.10，2.13，2.15，2.13，2.12，2.13，2.10， 2.15，2.12，2.14，2.10，2.13，2.11，2.14，2.11，设 零件长度分布为正态分布，试求总体的 90％的置信 区间：（1）若  0.01( ) cm ，（2）若 未知。 解： (1)   0.01已知 置信区间为 2 X z n          而 ， x n    2.125, 16, 0.01, 0.10   0.05 2 z z 1.645    2 z 0.004 n   故  置信区间为   2.121,2.129 解： (2) 未知，则 置信区间为 2 ( 1) S X tn n          2 0.0044 2.125, 16, , 0.10 15 而 ， x nS     0.05 2 tn t ( 1) (15) 1.7531     2 ( 1) 0.0075 S t n n 故    置信区间为 2.1175, 2.1325 解 ( 0.05) ? 0.01, 16 , 12.7, 0.0025 , , ( , ), 2 2       问此仪器工作是否稳定 今抽测 个点 算得 现对该区进行磁测 按仪器规定其方差不得 超过 设某异常区磁场强度服 从正态分布 x s N n  16,   0.05, (15) 27.5, 2  0.025   0 2 .975 (15)  6.26, 2 的1 置信区间为              ( 1) ( 1) , ( 1) ( 1) 2 1 / 2 2 2 / 2 2 n n S n n S      (0.00136, 0.00599), 0.01, . 由于方差 2 不超过 故此仪器工作稳定 3) 3）某厂利用两条自动化流水线灌装番茄酱，分别以两 条流水线上抽取样本： 1 2 12 XX X , ,,  及 1 2 17 YY Y ,,,  算出 2 2 1 2 X gY gS S    10.6( ), 9.5( ), 2.4, 4.7，假设这两 条流水线上灌装的番茄酱的重量都服从正态分布，且相 互独立，其均值分别为 1 2  , ,  （1）设两总体方差 2 2  1 2   ， 求1 2   置信度为95％的置信区间；（2）求 2  1 / 2  2的置信 度为95％的置信区间。 解： (1) 置信区间为 1 2 2 1 2 1 1 XY S t n n ( 2) n n               4) (书P293，习题16)   0.05， 1 2 0.025 2 tnn t ( 2) (27) 2.0518,    置信区间为   0.401, 2.601 2 2 1 12 2 1 2 ( 1) ( 1) ( 2) n Sn S S n n       其中 2 2 1 2 X gY g S S    10.6( ), 9.5( ), 2.4, 4.7 1 2 12 n n nn     12, 17, 2 27, X Y  1.1, 1 2 2 1 2 1 1 S tnn ( 2) 1.501 n n       解： (2) 置信区间为 2 2 1 1 2 2 2 12 2 12 1 2 2 1 1 , ( 1, 1) ( 1, 1) S S SFn n SF n n                 0.05， 1 2 0.025 2 F ( 1, 1) (11,16) 2.94 nn F    2 2 1 2 S S  2.4, 4.7  12 1 2 nn n n  12, 17, 1 11, 1 16,    1 2 1 2 2 1 0.025 2 1 11 ( 1, 1) ( 1, 1) (16,11) 3.33 Fn n Fn n F          置信区间为 0.1737, 1.7004 备用例题