
稳定性模型 1捕鱼业的持续收获 2种群的相巨竞争 3种群的相巨依存 4种群的弱肉强食 教学建模
稳定性模型 1 捕鱼业的持续收获 2 种群的相互竞争 3 种群的相互依存 4 种群的弱肉强食

稳定性模型 ·对象仍是动态过程,而建模目的是研究时 间充分长以后过程的变化趋势—平衡状 态是否稳定。 ·不求解微分方程,而是用微分方程稳定性 理论研究平衡状态的稳定性。 款学建模
稳定性模型 • 对象仍是动态过程,而建模目的是研究时 间充分长以后过程的变化趋势 ——平衡状 态是否稳定。 • 不求解微分方程,而是用微分方程稳定性 理论研究平衡状态的稳定性

捕鱼业的持续收获 背景 ·再生资源(渔业、林业等)与 非再生资源(矿业等) ·再生资源应适度开发—在持续稳 产前提下实现最大产量或最佳效益。 问题 。在捕捞量稳定的条件下,如何控制捕捞 及穷 使产量最大或效益最佳。 ·如果使捕捞量等于自然增长量,渔场鱼量 将保持不变,则捕捞量稳定。 数学建模
1 捕鱼业的持续收获 • 再生资源(渔业、林业等)与 非再生资源(矿业等) • 再生资源应适度开发——在持续稳 产前提下实现最大产量或最佳效益。 问题 及 分 析 • 在捕捞量稳定的条件下,如何控制捕捞 使产量最大或效益最佳。 • 如果使捕捞量等于自然增长量,渔场鱼量 将保持不变,则捕捞量稳定。 背景

产量模型 x()~渔场鱼量 假设 ·无捕捞时鱼的自然增长服从Logistic规律 ()=(w=xl-表) r~固有增长率,N~最大鱼量 ·单位时间捕捞量与渔场鱼量成正比 hc)=Ex,E捕捞强度 建模 记F(x)=f(x)-h(x) 捕捞情况下 渔场鱼量满足 )=F()=ml-3-E ,不需要求解0,只需知道x0稳定的条得 数学建模
Ex N x x(t) = F(x) = rx(1− ) − ( ) ( ) (1 ) N x x t = f x = rx − 记 F(x) = f (x) − h(x) 产量模型 假设 • 无捕捞时鱼的自然增长服从 Logistic规律 • 单位时间捕捞量与渔场鱼量成正比 建模 捕捞情况下 渔场鱼量满足 • 不需要求解x(t), 只需知道x(t)稳定的条件 r~固有增长率, N~最大鱼量 h(x)=Ex, E~捕捞强度 x(t) ~ 渔场鱼量

复习:一阶微分方程的平衡点及其稳定性 =F(x) 一阶非线性(自治)方程 Fx)=0的根x,微分方程的平衡点 =0xx 设x(①)是方程的解,若从x某邻域的任一初值出发, 都有1imx(t)=x,称x是方程(1)的稳定平衡点 不求x(①,判断x,稳定性的方法—直接法 (1)的近似线性方程 文=F'(x)x-x) (2) F'(x,)0→x,不稳定(对(2),(1) 教学建模
复习:一阶微分方程的平衡点及其稳定性 x = F(x) (1) 一阶非线性(自治)方程 F(x)=0的根x0 ~微分方程的平衡点 0 0 0 x x x x=x = 设x(t)是方程的解,若从x0 某邻域的任一初值出发, 都有 lim ( ) , 0 x t x t = → 称x0是方程(1)的稳定平衡点 不求x(t), 判断x0稳定性的方法——直接法 ( )( ) (2) 0 0 (1)的近似线性方程 x = F x x − x ( ) 0 ( (2),(1)) F x0 x0 稳定 对 ( ) 0 ( (2),(1)) F x0 x0 不稳定 对

产量模型 0=F()=x0-文)- F(x)=0 子宽这x=-台.x=0 平衡点 稳定性判断 F()=E-r,F(x)=r-E E0,稳定,x不稳定 E>r→F(x)>0,F(x)<0x不稳定,x稳定 E~捕捞强度 固有增长率 x稳定,可得到稳定产量 x1稳定,渔场干枯 数学建棋
F(x) = 0 0 = (1− ), x1 = 0 r E x N F(x0 ) = E − r, F(x1 ) = r − E 产量模型 Ex N x x(t) = F(x) = rx(1− ) − 平衡点 E r F(x0 ) 0,F(x1 ) 0 E r F(x0 ) 0,F(x1 ) 0 x0 稳定, 可得到稳定产量 x1 稳定, 渔场干枯 E~捕捞强度 r~固有增长率 x0 稳定, x1 不稳定 x0 不稳定, x1 稳定 稳定性判断
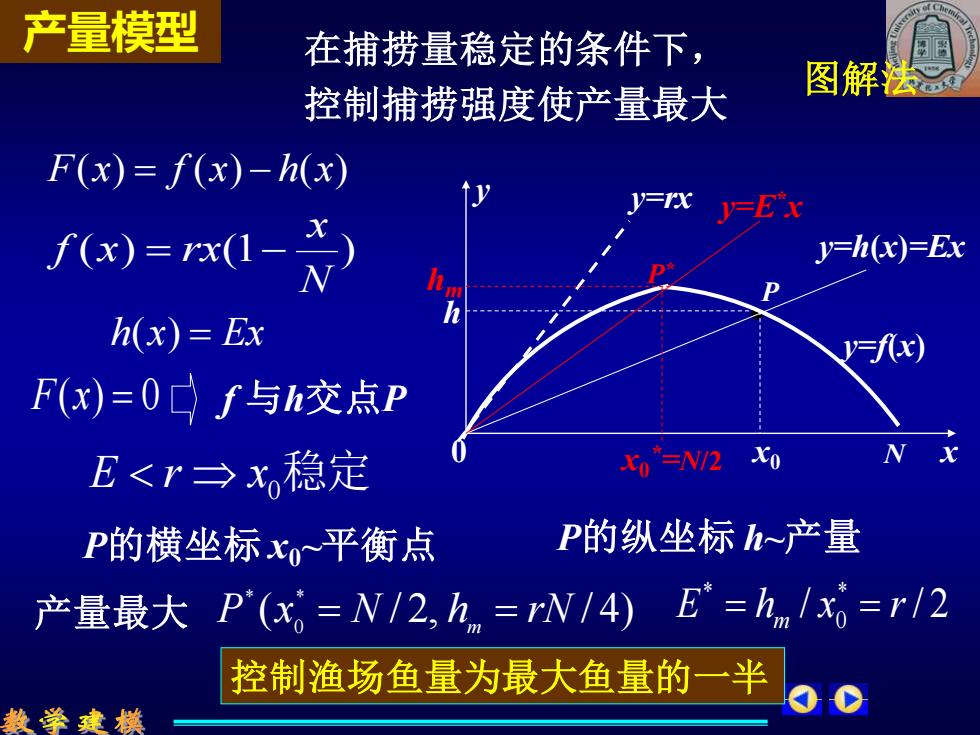
产量模型 在捕捞量稳定的条件下, 控制捕捞强度使产量最大 图解法 F(x)=f(x)-h(x) y-E'x f)=I-) y=h(x)=Ex h(x)=Ex y=fx) F(x)=0口f与h交点P E<r→x稳定 X=N/2 X0 P的横坐标x平衡点 P的纵坐标h~产量 产量最大P(x,=N/2,h=rW/4)E=hn/x=r/2 控制渔场鱼量为最大鱼量的一半 数学建模
产量模型 在捕捞量稳定的条件下, 控制捕捞强度使产量最大 图解法 F(x) = f (x) − h(x) ( ) (1 ) N x f x = rx − h(x) = Ex F(x) = 0 P的横坐标 x0~平衡点 / / 2 * 0 * E h x r = m = y=rx h P x0 y 0 y=h(x)=Ex N x y=f(x) P的纵坐标 h~产量 ( / 2, / 4) * 0 * 产量最大 P x = N h m = rN f 与h交点P E r x0 稳定 hm x0 * =N/2 P* y=E* x 控制渔场鱼量为最大鱼量的一半

效益模型 在捕捞量稳定的条件下,控制捕捞 强度使效益最大 假设 ·鱼销售价格p ·单位捕捞强度费用c 收入T=phc)=pEx 支出S=cE 单位时间利润R=T-S=pEx一cE 稳定平衡点x,=N(1-E/r) R(E)=T(E)-S(E)=pNE(-E)-cE 求E使Rub最大E:=50-六)<E=2 渔场 鱼量 (1 数学建模 8W
cE r E R(E) = T(E) − S(E) = pNE(1− ) − (1 ) 4 2 2 2 p N rN c hR = − R = T − S = pEx − cE 效益模型 假设 • 鱼销售价格p • 单位捕捞强度费用c 单位时间利润 在捕捞量稳定的条件下,控制捕捞 强度使效益最大. (1 / ) 0 稳定平衡点 x = N − E r 求E使R(E)最大 (1 ) 2 pN r c ER = − p N c 2 2 (1 ) = + r E x N R 渔场 R = − 鱼量 2 * r E = 收入 T = ph(x) = pEx 支出 S = cE

捕捞 ·封闭式捕捞追求利润R(E)最大 过 ER ·开放式捕捞只求利润R(E)>0 R(E)=T(E)-S(E)=pNE(1- R(E)=0时的捕捞强度(临界强度)E,=2ER 临界强度下的渔场鱼量 x,=N0-) S(E) p↑,c↓dE,↑,x T(E) 捕捞过度 ER E* E 数学建模
Es S(E) T(E) 0 r E 捕捞 过度 • 封闭式捕捞追求利润R(E)最大 • 开放式捕捞只求利润R(E) > 0 cE r E R(E) = T(E) − S(E) = pNE(1− ) − R(E)=0时的捕捞强度(临界强度) Es=2ER (1 ) r E x N s s = − p c = 临界强度下的渔场鱼量 p ,c 捕捞过度 ER (1 ) 2 pN r c ER = − E* 令 ==0 (1 ) pN c E r s = − Es , xs

2种群的相互竞争 ·一个自然环境中有两个种群生存,它们之间的 关系:相互竞争;相互依存;弱肉强食。 ·当两个种群为争夺同一食物来源和生存空间相 互竞争时,常见的结局是,竞争力弱的灭绝, 竞争力强的达到环境容许的最大容量。 ·建立数学模型描述两个种群相互竞争的过程, 分析产生这种结局的条件。 数学建棋
2 种群的相互竞争 • 一个自然环境中有两个种群生存,它们之间的 关系:相互竞争;相互依存;弱肉强食。 • 当两个种群为争夺同一食物来源和生存空间相 互竞争时,常见的结局是,竞争力弱的灭绝, 竞争力强的达到环境容许的最大容量。 • 建立数学模型描述两个种群相互竞争的过程, 分析产生这种结局的条件