
第三节 建模示例
第三节 建模示例

雨中行走问题:天将下雨,从寝 里到教室有一段约一公里的路程。没 拿雨具就下了楼,出了宿舍门,可刚走几 步,天就下起大雨来。由于时间紧急,决 定冒雨行走,问你将被淋得多湿? 问题看起来很简单,只要跑得越快被淋 湿的程度越低。果真如此吗?
雨中行走问题:天将下雨,从寝 室到教室有一段约一公里的路程。没 拿雨具就下了楼,出了宿舍门,可刚走几 步,天就下起大雨来。由于时间紧急,决 定冒雨行走,问你将被淋得多湿? 问题看起来很简单,只要跑得越快被淋 湿的程度越低。 果真如此吗?

☐模型准备与假设 建模目的:给定特定的降雨条件,能否设 计一个方案使你被雨淋得最少? 为简化问题,假设人所走的路线是直线,将 人体视为长方体,设走速、雨速均为常数
为简化问题,假设人所走的路线是直线,将 人体视为长方体,设走速、雨速均为常数。 q模型准备与假设 建模目的:给定特定的降雨条件,能否设 计一个方案使你被雨淋得最少?

与此问题有关的因素: 因素 符号 单位 淋雨时间 雨速 +L 秒 米/秒 雨的角度(由于有风) 6 走速 米/秒 人的高度 h 人的宽度 人的厚度 淋雨量 雨的强度 300-0 行走的距离 米
q与此问题有关的因素: 因素 淋雨时间 雨速 雨的角度(由于有风) 走速 人的高度 人的宽度 人的厚度 淋雨量 雨的强度 行走的距离 符号 t r θ v h w d C I D 单位 秒 米/秒 度 米/秒 米 米 米 升 米

口通过查资料、调查后,选取一组比较典 型的数据:雨速=4米/秒;走速=2米/秒; 跑速=6米/秒;降雨量=2厘米/小时
q通过查资料、调查后,选取一组比较典 型的数据:雨速=4米/秒;走速=2米/秒; 跑速=6米/秒; 降雨量= 2厘米/小时

口建立模型 看先建一个尽可能简单的模型。 不考虑雨向,即认为雨是垂直而下。若 在整个过程中你的跑速均为6米/秒 ■淋雨时间=1000÷6≈167(秒)=2分47秒 当降雨量为每小时2厘米,则2分47秒中的 降雨量为 2×0.01×167÷3600(米)
q建立模型 首先建一个尽可能简单的模型。 不考虑雨向,即认为雨是垂直而下。若 在整个过程中你的跑速均为6米/秒 §淋雨时间=1000÷6≈167(秒)=2分47秒 当降雨量为每小时2厘米,则2分47秒中的 降雨量为 2×0.01×167÷3600(米)

取入高为15米、宽为0.5米、厚为 02米,则人体可能淋到雨的总表面 积为2.2米2 ■淋雨量=降雨量X淋到雨的总表面积 ≈2.041升) 为较接近实际情况,去掉雨是垂直而下的假设 雨速和雨量是有区别的,引入雨的强度概念 来描述雨量的大小
若取人高为1.5米、宽为0.5米、厚为 0.2米,则人体可能淋到雨的总表面 积为2.2 米2 §淋雨量=降雨量×淋到雨的总表面积 ≈2.041(升) 为较接近实际情况,去掉雨是垂直而下的假设 雨速和雨量是有区别的 ,引入雨的强度概念 来描述雨量的大小

口定义: 雨的强度[= 降雨量 雨速 雨速为4米/秒,降雨量为2厘米/小、附, 则 1 7.2×10 雨的强度反映了雨的大小: 1=0,说明没有雨 1=1,是暴雨
q定义: 雨的强度 雨速 降雨量 I = 雨速为4米/秒,降雨量为2厘米/小时,则 5 7.2 10 1 ´ I = 雨的强度反映了雨的大小: 说明没有雨 , I=1, I=0, 是暴雨
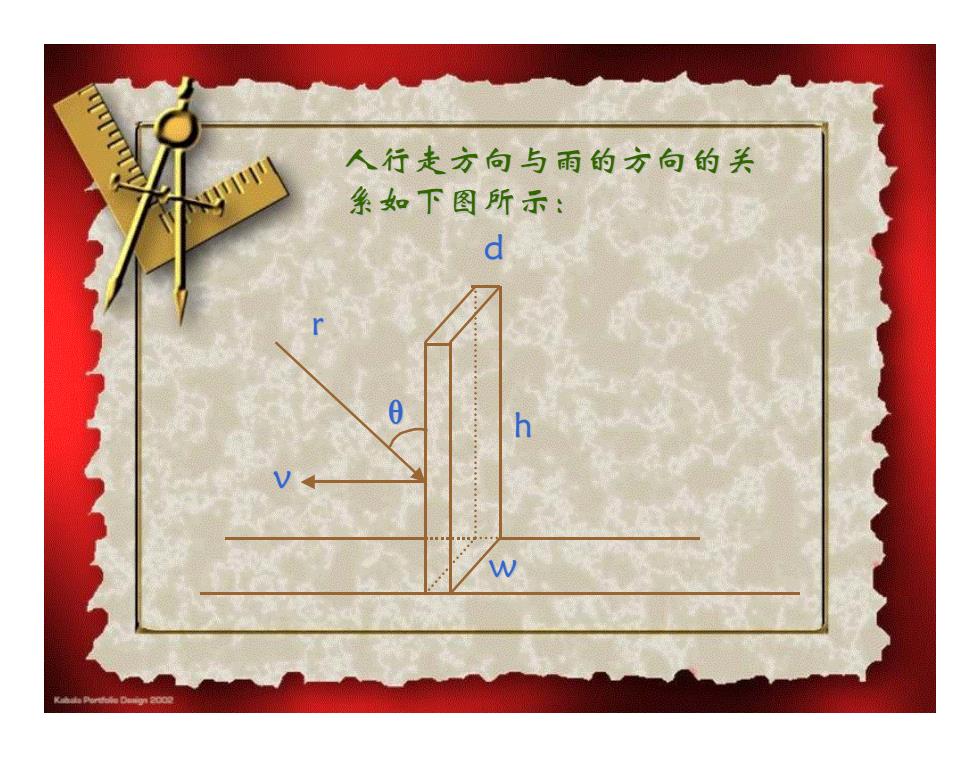
人行走方向与雨的方向的关 象如下图所示: d h W
人行走方向与雨的方向的关 系如下图所示: d h w v r θ

于雨是呈一个角度下来的,在这种 情况下受雨面仅为人体的顶部和前 部。故淋在人身上的雨量可以分两种 情况来计算: 考虑人的顶部顶部的表面积=wd米2 雨速的竖直分量=rcos0米/秒 单位时间内的淋雨量,即 淋雨率=强度×面积×雨速=wdr cos米3/秒 在时间t=D/y中的淋雨量-Dhvdrcos (米) (1.3.1)
由于雨是呈一个角度下来的,在这种 情况下受雨面仅为人体的顶部和前 部。故淋在人身上的雨量可以分两种 情况来计算: 顶部的表面积 = 米2 wd 雨速的竖直分量= r cosq 米 秒 单位时间内的淋雨量,即 在时间 t = D v 中的 淋雨量 ( ) cos 米3 v DIwdr q = (1.3.1) 淋雨率 = 强度´面积´雨速 = Iwdr cosq米3 /秒 (1)考虑人的顶部