
20 第五章 微分方程模型 第一讲传染病模型 款学建模
第五章 微分方程模型 第一讲 传染病模型

·描述对象特征随时间(空间)的演变过程 动态 棋型 ·分析对象特征的变化规律 ·预报对象特征的未来性态 ·研究控制对象特征的手段 微分 ·根据函数及其变化率之间的关系确定函数 方程 •根据建模目的和问题分析作出简化假设 建棋 ·按照内在规律或用类比法建立微分方程 数学建模
动态 模型 • 描述对象特征随时间(空间)的演变过程 • 分析对象特征的变化规律 • 预报对象特征的未来性态 • 研究控制对象特征的手段 微分 • 根据函数及其变化率之间的关系确定函数 方程 建模 • 根据建模目的和问题分析作出简化假设 • 按照内在规律或用类比法建立微分方程

模型1 传染病模型 问题 ·描述传染病的传播过程 ·分析受感染人数的变化规律 ·预报传染病高潮到来的时刻 ·预防传染病蔓延的手段 ·按照传播过程的一般规律, 用机理分析方法建立模型 数学建模
模型1 传染病模型 问题 • 描述传染病的传播过程 • 分析受感染人数的变化规律 • 预报传染病高潮到来的时刻 • 预防传染病蔓延的手段 • 按照传播过程的一般规律, 用机理分析方法建立模型

传染病模型 模型1 已感染人数(病人)) 假设 ·每个病人每天有效接触 (足以使人致病)人数为入 建模 i(t+△t)-i(t=2i(t)△ di =八i i(t)=i,e“ dt i(0)=0 0t>0→i->0? 若有效接触的是病人, 必须区分已感染者(病 则不能使病人数增加 人)和未感染者(健康人) 教学建模
已感染人数 (病人) i(t) • 每个病人每天有效接触 (足以使人致病)人数为 模型1 假设 i(t + t) −i(t) = i(t)t 若有效接触的是病人, 则不能使病人数增加 必须区分已感染者(病 人)和未感染者(健康人) 建模 0 i(0) i i dt di = = t → i → t i t i e 0 ( ) = ? 传染病模型

传染病模型 模型2 区分已感染者(病人)和未感染者(健康人) 假设 1)总人数N不变,病人和健康 人的比例分别为i(t),s(t) SI模型 2)每个病人每天有效接触人数 2~日 为几,且使接触的健康人致病 接触率 建模 N[i(t+△t)-i(t)]=[2s(t)]Ni(t)△t di Asi di dt dt =2(1-) s(t)+i(t)=1 i(0)=i。 数学建模
si dt di = s(t) + i(t) =1 模型2 区分已感染者(病人)和未感染者(健康人) 假设 1)总人数N不变,病人和健康 人的 比例分别为 i(t),s(t) 2)每个病人每天有效接触人数 为, 且使接触的健康人致病 建模 N[i(t + t) −i(t)] =[s(t)]Ni(t)t = = − 0 (0) (1 ) i i i i dt di ~ 日 接触率 SI 模型 传染病模型
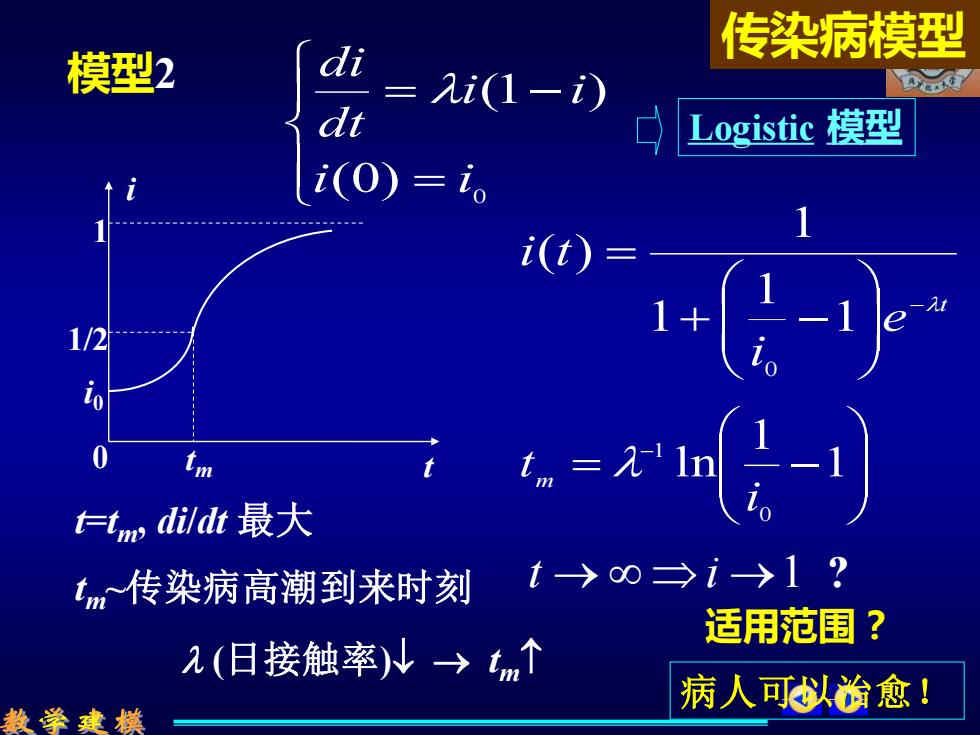
传染病模型 模型2 di =入i(1-) Logistic模型 i(0)=。 i(t) 1/2 1+ tm n=元'lm t dildt最大 tm传染病高潮到来时刻 t→0→i→1? 适用范围? 2(日接触率)N→tm个 病人可以治愈! 数学建模
t e i i t − + − = 1 1 1 1 ( ) 0 = = − 0 (0) (1 ) i i i i dt di 模型 2 1/2 tm i i0 1 0 t = − − 1 1 ln 0 1 i t m tm~传染病高潮到来时刻 (日接触率) → tm t → i →1 Logistic 模型 病人可以治愈! ? t=tm, di/dt 最大 传染病模型 适用范围?

传染病模型 模型3 传染病无免疫性—病人治愈成 为健康人,健康人可再次被感染 SIS模型 增加假设 3)病人每天治愈的比例为4 4~日治愈率 建模 W[i(t+△t)-i(t)]=2Ns(t)i(t)△t-Ni(t)△i di =入i(1-)-10 入~日接触率 i(0)=i。 1/4~感染期 o=λ/4 。~一个感染期内每个病人的 有效接触人数,称为接触数。 数学建模
模型3 传染病无免疫性——病人治愈成 为健康人,健康人可再次被感染 增加假设 SIS 模型 3)病人每天治愈的比例为 ~日治愈率 建模 N[i(t + t) −i(t)] = Ns(t)i(t)t − Ni(t)t = / ~ 日接触率 1/ ~感染期 ~ 一个感染期内每个病人的 有效接触人数,称为接触数。 = = − − 0 (0) (1 ) i i i i i dt di 传染病模型
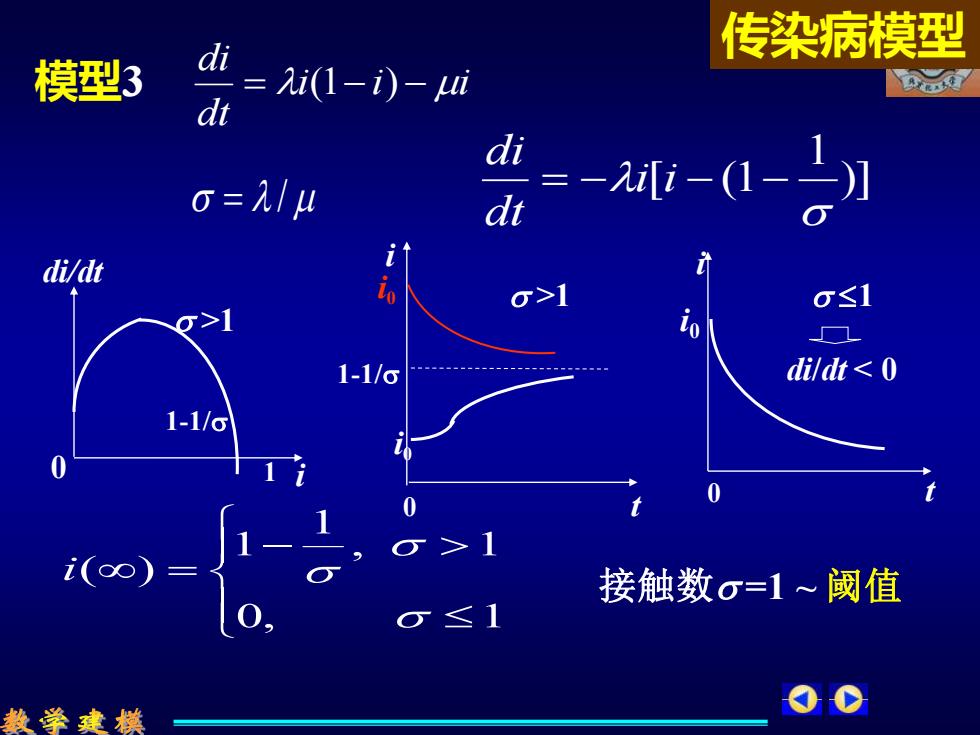
传染病模型 模型3 0-9Fn o=214 台-0-刘 di/dt o>1 o≤1 1-1/o dildt 0 1-1/o i(oo) 接触数σ=1~阈值 o≤1 数学建模
− = 0, 1 , 1 1 1 ( ) i )] 1 [ (1 = −i i − − dt di 模型3 i0 i0 接触数 =1 ~ 阈值 = / 1-1/ i0 i i i dt di = (1− ) − i di/dt 0 1 >1 0 t i >1 1-1/ i 0 t 1 di/dt < 0 传染病模型

0=214 传染病模型 o>1 小 →(t)按S形曲线增长 感染期内有效接触感染的 o≤1 →(t)↓ 健康者人数不超过病人数 2~日接触率 -反映地区的卫生水平 4~日治愈率 -反映地区的医疗水平 结果解释:提高卫生水平和医疗水平都可以 有效控制传染病的蔓延! 模型2(SI模型如何看作模型3(SIS模型)的特例? 数学建模
0小 1 i i(t)按S形曲线增长 感染期内有效接触感染的 健康者人数不超过病人数 模型2(SI模型)如何看作模型3(SIS模型)的特例? 传染病模型 1 i(t) ~ 日接触率 = / ~日治愈率 --反映地区的卫生水平 --反映地区的医疗水平 结果解释:提高卫生水平和医疗水平都可以 有效控制传染病的蔓延!

模型4 传染病模型 传染病有免疫性—病人治愈 后即移出感染系统,称移出者 SR模型 假设 1)总人数N不变,病人、健康人和移 出者的比例分别为i(t),s(t),r(t) 2)病人的日接触率孔,日治愈率山, 接触数σ=见/4 建模 s(t)+i(t)+r(t)=1 需建立i(t),s(t),r(t)的两个方程 数学建模
模型4 传染病有免疫性——病人治愈 后即移出感染系统,称移出者 SIR模型 假设 1)总人数N不变,病人、健康人和移 出者的比例分别为 i(t),s(t),r(t) 2)病人的日接触率 , 日治愈率, 接触数 = / 建模 s(t) + i(t) + r(t) =1 需建立 i(t),s(t),r(t) 的两个方程 传染病模型