
第五章 微分方程模型 1经济增长模型 2正规战与游击战 3药物在体内的分布与排除 4香烟过滤嘴的作用 教学建模
第五章 微分方程模型 1 经济增长模型 2 正规战与游击战 3 药物在体内的分布与排除 4 香烟过滤嘴的作用

20 经济增长模型 增加投资 增加生产 增加劳动力 发展经济 提高技术 建立产值与资金、劳动力之间的关系 研究资金与劳动力的最佳分配,使投资效益最大 ·调节资金与劳动力的增长率,使经济(生产率)增长 款学建模
经济增长模型 增加生产 发展经济 增加投资 增加劳动力 提高技术 • 建立产值与资金、劳动力之间的关系 • 研究资金与劳动力的最佳分配,使投资效益最大 • 调节资金与劳动力的增长率,使经济(生产率)增长 目 标

1.道格拉斯(Douglas)生产函数 产值 资金K() 劳动力L() 2) 技术)=0 (t)=fF(K(t),L(t)) F为待定函数 静态模型 (K,L)=fF(K,L) 每个劳动 每个劳动 K 力的产值 y= 力的投资 数学建模
1. 道格拉斯(Douglas)生产函数 产值 Q(t) ( ) ( ( ), ( )) 0 Q t = f F K t L t 资金 K(t) 劳动力 L(t) 技术 f(t) = f0 F为待定函数 每个劳动 力的产值 L Q z = 每个劳动 力的投资 L K y = 静态模型 ( , ) ( , ) Q K L = f 0 F K L
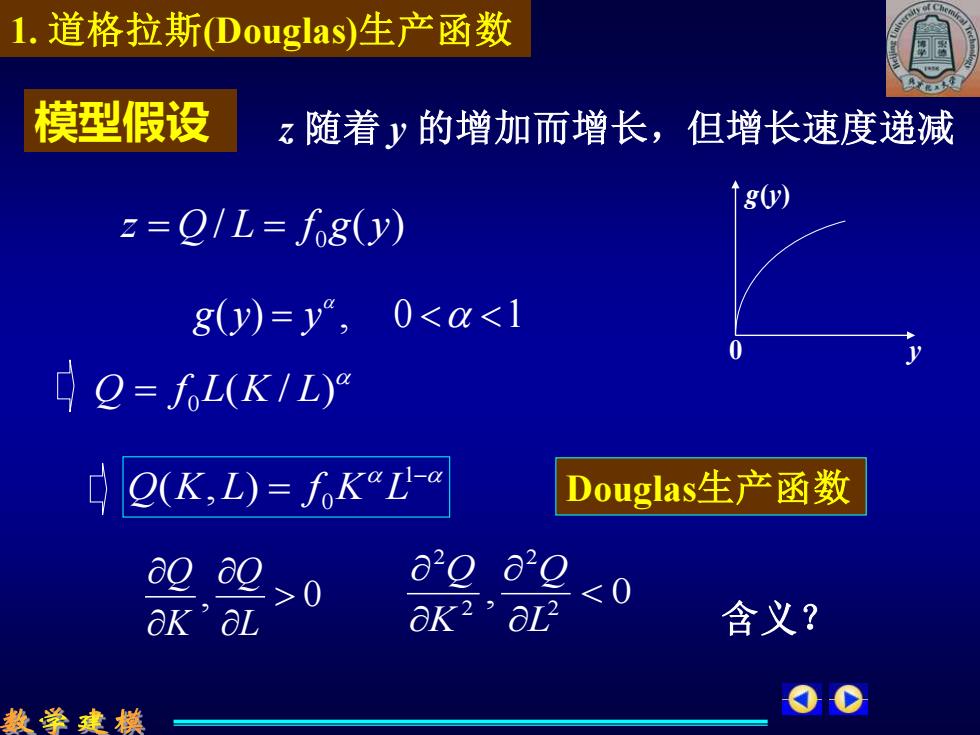
1.道格拉斯Douglas)生产函数 模型假设 z随着y的增加而增长,但增长速度递减 g(v) z=0/L=fg(y) gy)=y,0o .<0 ok'aL 含义? 数学建模
/ ( ) 0 z = Q L = f g y ( ) = , 0 1 g y y , 0 L Q K Q 模型假设 z 随着 y 的增加而增长,但增长速度递减 y g(y) 0 1. 道格拉斯(Douglas)生产函数 含义? , 0 2 2 2 2 L Q K Q ( / ) Q = f 0 L K L Q(K,L) = f 0 K L 1− Douglas生产函数

1.Douglas生产函数 O(K,L=fK“Z- Qx~单位资金创造的产值 =0, L0=1-0 Q~单位劳动力创造的产值 KOk +LOL=O α~资金在产值中的份额1-a~劳动力在产值中的份额 更一般的道格拉斯①ouglas)生产函数 Q(K,L)=fK,00 数学建模
− = 1 0 Q(K,L) f K L QK ~ 单位资金创造的产值 QL ~ 单位劳动力创造的产值 ~ 资金在产值中的份额 1- ~劳动力在产值中的份额 更一般的道格拉斯(Douglas)生产函数 ( , ) , 0 , 1, 0 Q K L = f 0 K L f 0 1. Douglas生产函数 =, =1− Q LQ Q KQK L KQK + LQL = Q

2) 资金与劳动力的最佳分配(静态模型) 资金来自贷款,利率r 劳动力付工资 资金和劳动力创造的效益 S=Q-rK-WL 求资金与劳动力的分配比例KL(每个 劳动力占有的资金),使效益$最大 as as aK 0 W 号a号8-长 1-a r w个,r↓,a↑ 数学建棋 KL
0, = 0 = L S K S =, =1− Q LQ Q KQK L r w L K − = 1 w , r , K/L 求资金与劳动力的分配比例K/L(每个 劳动力占有的资金) ,使效益S最大 资金和劳动力创造的效益 S = Q − rK − wL 资金来自贷款,利率 r 劳动力付工资 w 2)资金与劳动力的最佳分配(静态模型) − = K 1 L Q Q L K w r Q Q L K =

3)经济(生产率)增长的条件(动态模型 要使Q(0或Z(0=0L(①增长,K(),L(0应满足的案裤 模型 ·投资增长率与产值成正比 假设 (用一定比例扩大再生产) dK dt =20,元>0 •劳动力相对增长率为常数 L(t)=Le" 数学建模
3) 经济(生产率)增长的条件 (动态模型) 要使 Q(t) 或 Z(t)=Q(t)/L(t) 增长, K(t), L(t)应满足的条件 模型 假设 • 投资增长率与产值成正比 (用一定比例扩大再生产) • 劳动力相对增长率为常数 = Q, 0 dt dK L dt dL = t L t L e 0 ( ) =

3)经济(生产率)增长的条件(动态模型 国 dK dt =20,元>0 e=fLg(y)g(y)=y" dK dt =AfoLy" K y= K=Ly dt dyuly 数学建模
( ) 0 Q = f Lg y g(y) = y f Ly dt dK = 0 K Ly L K y = , = Ly dt dy L dt dK = + 3) 经济(生产率)增长的条件 (动态模型) = Q, 0 dt dK L dt dL =

3)经济(生产率)增长的条件(动态模型 dK dt =f Ly" y +0y=f02y d =+ dt Bernoulli方程 dt dt w-(2w 。=K,/L,Q=fKgL,K。=20 =f刘 数学建模
f Ly dt dK = 0 Ly dt dy L dt dK = + y f y dt dy + = 0 Bernoulli方程 − − − − = + − 1 1 1 0 (1 ) 0 0 ( ) ( ) t e f y f y t 0 0 1 0 0 0 0 0 0 0 y K / L , Q f K L , K Q = = = − 0 0 0 1 0 K K y f = − 3) 经济(生产率)增长的条件 (动态模型)

3)经济(生产率)增长的条件(动态模型 0-{-0-} 产值Q0增长 日doh>0 O=fLg(y) 品-eo岛*/s 8(y)=y foLy2 [foan+u(1-a)y#] 款学建模
− − − = − − 1 1 (1 ) 0 0 0 ( ) [1 (1 ) ] t e K f K y t 3) 经济(生产率)增长的条件 (动态模型) 产值Q(t)增长 dQ/dt > 0 g y y Q f Lg y = = ( ) ( ) 0 dt dL f g y dt dy f Lg y dt dQ ( ) ( ) 0 + 0 = [ (1 ) ] 1 0 2 1 0 − − = f Ly f + − y