
第八节利用自由曲面建模 款学建模
第八节 利用自由曲面建模

自由曲面的建模也是从构造曲线开始的,当所需的 由曲线构造完毕后,就可利用这些曲线来构造自由曲 面了,最后将得到的各曲面片进行拼接、光滑处理, 从而构造出所要的模型。整个构造过程如下: 用自由曲线的生成工具描绘U方向曲线 用自由曲线的生成工具描绘V方向曲线 (3) 定义U方向曲线的顺序 (4) 定义V方向曲线的顺序 ) 构造初始曲面片 进行曲面的拼接、光滑处理 曲面后处理 数学建模
自由曲面的建模也是从构造曲线开始的,当所需的自 由曲线构造完毕后,就可利用这些曲线来构造自由曲 面了,最后将得到的各曲面片进行拼接、光滑处理, 从而构造出所要的模型。整个构造过程如下: 用自由曲线的生成工具描绘 方向曲线 用自由曲线的生成工具描绘 方向曲线 (3) 定义 方向曲线的顺序 (4) 定义 方向曲线的顺序 (5) 构造初始曲面片 (6) 进行曲面的拼接、光滑处理 (7) 曲面后处理 U V V U
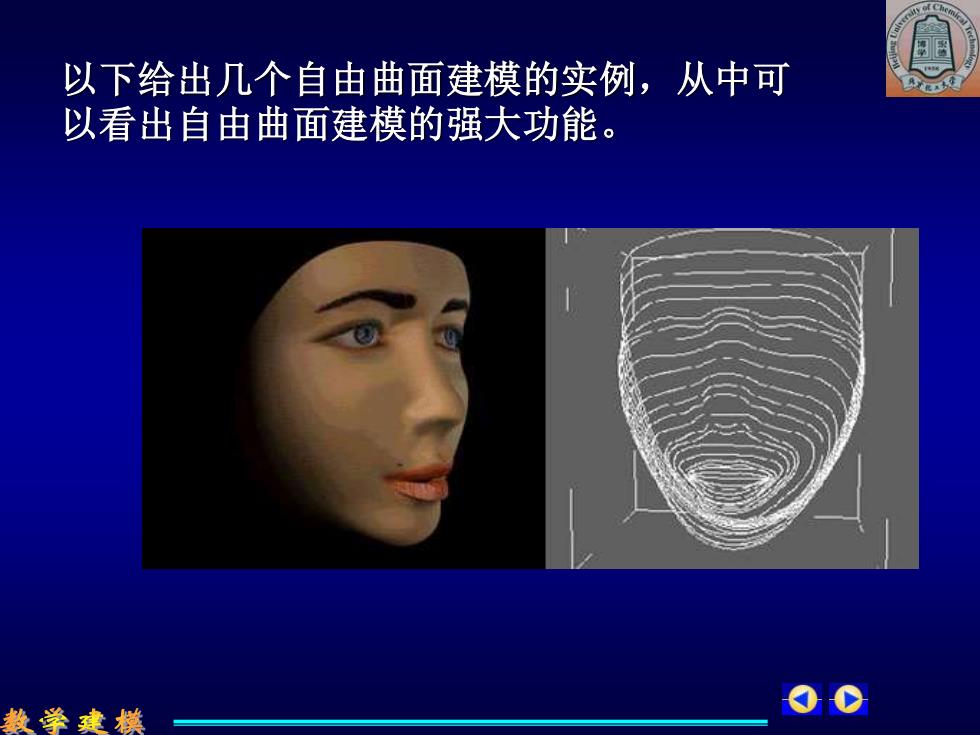
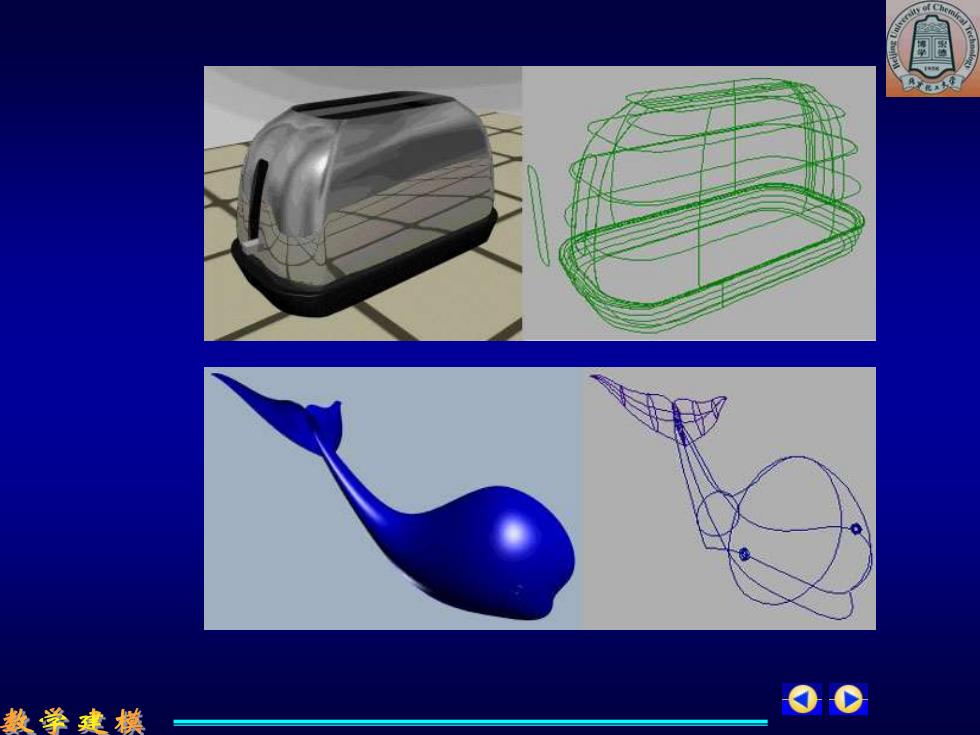
以下给出几个自由曲面建模的实例,从中可 以看出自由曲面建模的强大功能。 数学建模一 O
以下给出几个自由曲面建模的实例,从中可 以看出自由曲面建模的强大功能

00 数学建模
20 款学建模

自由形体变换示例 在某些场合下,模型的形状用前面的方法难以实 现,我们称这种形态为自由型物体。要建立这种 模型是十分耗时的,因为它的生成过程就象雕塑 家完成一个雕塑作品一样,需要在简单的模型表 面上进行许多局部的拉压与揉和等多种变换,最 终得到所需的形态。自由型物体的建模在第六节 有较详细的叙述,现在仅介绍几种自由型物体的 变换方法。 教学建模
自由形体变换示例 在某些场合下,模型的形状用前面的方法难以实 现,我们称这种形态为自由型物体。要建立这种 模型是十分耗时的,因为它的生成过程就象雕塑 家完成一个雕塑作品一样,需要在简单的模型表 面上进行许多局部的拉压与揉和等多种变换,最 终得到所需的形态。自由型物体的建模在第六节 有较详细的叙述,现在仅介绍几种自由型物体的 变换方法

例6.7.1直接点操作 最常见、最容易的创建三维自由型物体的方法是从 现有的三维结构(多边形或基于样条)开始,这些结 构可以被雕刻或转换成希望的物体。这个虚拟的雕 刻过程非常类似于用手塑造新粘土的过程。粘土的 最初形状对于期望的最后三维形状来说是不重要的。 随着手的推拿、压、拉和磨平,不成形的胶泥最终 变成有意义的结构。 款学建模
例6.7.1 直接点操作 最常见、最容易的创建三维自由型物体的方法是从 现有的三维结构(多边形或基于样条)开始,这些结 构可以被雕刻或转换成希望的物体。这个虚拟的雕 刻过程非常类似于用手塑造新粘土的过程。粘土的 最初形状对于期望的最后三维形状来说是不重要的。 随着手的推拿、压、拉和磨平,不成形的胶泥最终 变成有意义的结构

例6.7.2变形网络FFT 还有另一种比直接点操作更适用于任务的自由模 型技术,特别在需要统一的总体变形,或用户没有技 术或时间一次处理大量的点时使用。这一技术被称作 网格变形技术FFT(free form transforma)。网格有时 也被称为边界框。 网格是一个点和线的结构,它控制模型中的点。可 以将网格考虑成一个格子结构,这些格子用想象中的 弹簧连接到模型中的点上。因此,当移动格子或格子 上的点时,也拖动物体中的点随它们一起移动。 数学建模
例 6.7.2 变形网络FFT 还有另一种比直接点操作更适用于任务的自由模 型技术,特别在需要统一的总体变形,或用户没有技 术或时间一次处理大量的点时使用。这一技术被称作 网格变形技术FFT(free form transforma)。网格有时 也被称为边界框。 网格是一个点和线的结构,它控制模型中的点。可 以将网格考虑成一个格子结构,这些格子用想象中的 弹簧连接到模型中的点上。因此,当移动格子或格子 上的点时,也拖动物体中的点随它们一起移动
例6.7.3地形函数 有许多技术可用于创作地形,它们模拟或再现自 然的或想象的大地表面。也有许多技术用于变形这些 地形,而这些技术使用数学函数。生成一个地形的最 简单的技术是使用一个带XY分量的二维平面。若希望 的形状像一个自然地形,则使用这些技术中的任何 个都是合适的;若设法创作一个更迷人的地形,则基 本平面可用数学函数变形。产生地形的另一项技术 是构造一个三维网格,它是以定义一个想象的或实际 的地形的二维轮廓为基础的。构造地形的这种技术对 数据非常敏感,而且对产生地形的精确模型也非常有 效。由于它们的拓扑细节,用这种技术产生的地形很 少用数学函数变形
例 6.7.3 地形函数 有许多技术可用于创作地形,它们模拟或再现自 然的或想象的大地表面。也有许多技术用于变形这些 地形,而这些技术使用数学函数。生成一个地形的最 简单的技术是使用一个带XY分量的二维平面。若希望 的形状像一个自然地形,则使用这些技术中的任何一 个都是合适的;若设法创作一个更迷人的地形,则基 本平面可用数学函数变形。 产生地形的另一项技术 是构造一个三维网格,它是以定义一个想象的或实际 的地形的二维轮廓为基础的。构造地形的这种技术对 数据非常敏感,而且对产生地形的精确模型也非常有 效。由于它们的拓扑细节,用这种技术产生的地形很 少用数学函数变形