
第三节插值与拟合 数学建模 00
第三节 插值与拟合

工程中,常有这样的问题:给一批数据点,需确 定满足特定要求的曲线或曲面。如果要求所求曲线(面) 通过所给所以数据点,这就是插值问题 当数据较多,插值函数是一个次数很高的函数,比较 复杂,同时,给定的数据一般是由观察测量所得,往 往带有随机误差,因而,求曲线(面)通过所有数据点 就既不现实也不必要。如果不要求曲线(面)通过所有 数据点,而是要求它反映对象整体的变化趋势,可得 到更简单实用的近似函数,这就是数据拟合 数学建模
工程中,常有这样的问题:给一批数据点,需确 定满足特定要求的曲线或曲面。如果要求所求曲线(面) 通过所给所以数据点,这就是插值问题 当数据较多,插值函数是一个次数很高的函数,比较 复杂,同时,给定的数据一般是由观察测量所得,往 往带有随机误差,因而,求曲线(面)通过所有数据点 就既不现实也不必要。如果不要求曲线(面)通过所有 数据点,而是要求它反映对象整体的变化趋势,可得 到更简单实用的近似函数,这就是数据拟合

一。 一 维插值 InterpI,y,cx,'method) Nearest: 最邻近点插值 Linear: 线性插值 Spline: 线性样条插值 cubic ,三次插值 x,一数据点的横纵坐标,x必须单调 x一需要插值的横坐标数据(或数组) cx不能超出x的范围 nethod--可选参数 教学建模
一. 一维插值 x,y—数据点的横纵坐标,x必须单调 cx—需要插值的横坐标数据(或数组), cx不能超出x的范围 method—可选参数 Interp1(x,y,cx,’method’) Nearest: 最邻近点插值 Linear: 线性插值 Spline: 线性样条插值 cubic : 三次插值
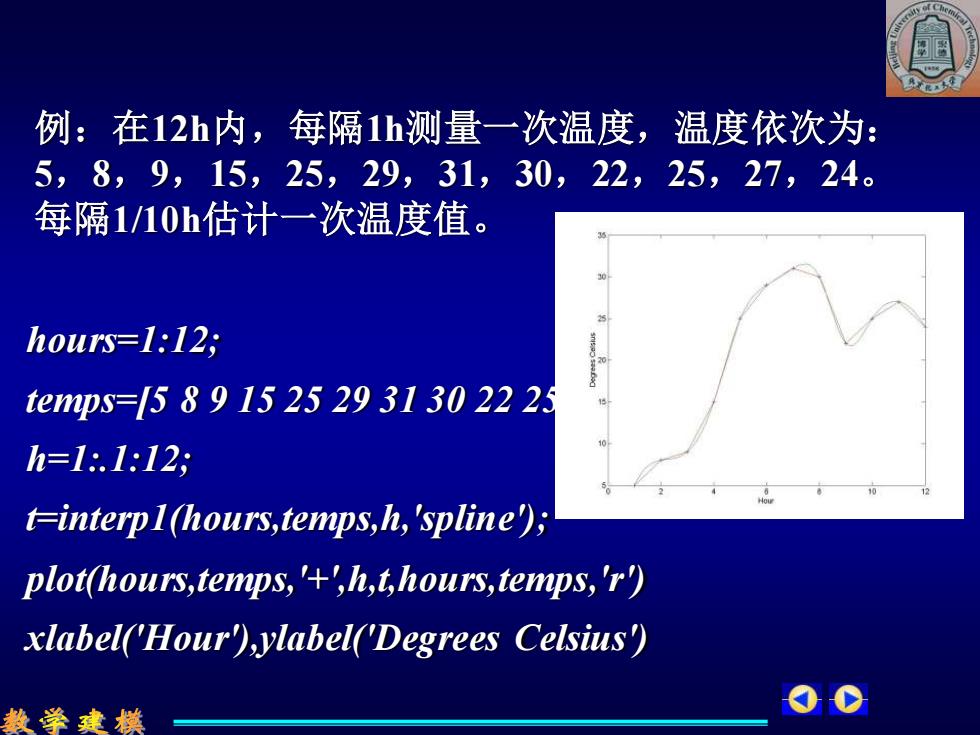
例:在12h内,每隔1h测量一次温度,温度依次为: 5,8,9,15,25,29,31,30,22,25,27,24。 每隔1/10h估计一次温度值。 hous=1:12; temps=-/58915252931302225 h=1:.1:l2; t-interpI(hours,temps,h,'spline); plot(hours,temps,',h,t,hours,temps,'r) xlabel(Hour),ylabel(Degrees Celsius) 数学建模
例:在12h内,每隔1h测量一次温度,温度依次为: 5,8,9,15,25,29,31,30,22,25,27,24。 每隔1/10h估计一次温度值。 hours=1:12; temps=[5 8 9 15 25 29 31 30 22 25 27 24]; h=1:.1:12; t=interp1(hours,temps,h,'spline'); plot(hours,temps,'+',h,t,hours,temps,'r') xlabel('Hour'),ylabel('Degrees Celsius')

二.二维插值 1.插值基点为网格节点 cz-interp2(x,y,3,cx,cy,'method') x一自变量,x,y必须单调递增 此,给定网格点的横坐标、纵坐标数据(或数组),一个 行向量,一个列向量Z是mXn维矩阵nethod一可选参数 Vearest:最邻近点插值 Linear:线性插值 Spline:三次样条插值 cubic:三次插值 教学建模
二. 二维插值 1.插值基点为网格节点 cz=interp2(x,y,z,cx,cy,’method’) x,y—自变量,x,y必须单调递增 cx,cy—给定网格点的横坐标、纵坐标数据(或数组),一个 行向量,一个列向量Z是m×n维矩阵method—可选参数 Nearest:最邻近点插值 Linear:线性插值 Spline:三次样条插值 cubic :三次插值

20 2.插值基点为散乱节点 c=griddata(x,y,,cx,cy,'method') Vearest:最邻近点插值 Linear: 线性插值 cubic 三次插值 V4: MATLAB:提供的方法 xy,Z是n维向量一指明所给数据点的横、纵、竖坐标 x,少一给定网格点的横坐标、纵坐标,一个行向量,一个列向量 method一可选参数 数学建模
2. 插值基点为散乱节点 cz=griddata(x,y,z,cx,cy,’method’) x,y, Z是n维向量—指明所给数据点的横、纵、竖坐标 cx,cy—给定网格点的横坐标、纵坐标,一个行向量,一个列向量 method—可选参数 Nearest: 最邻近点插值 Linear:线性插值 cubic : 三次插值 V4: MATLAB提供的方法

例:测得平板5×3网格点处的温度依次为: 8281808284 7963616581 8484828586 作出平板表面温度分布曲面。 教学建模
例:测得平板5×3网格点处的温度依次为: 82 81 80 82 84 79 63 61 65 81 84 84 82 85 86 作出平板表面温度分布曲面
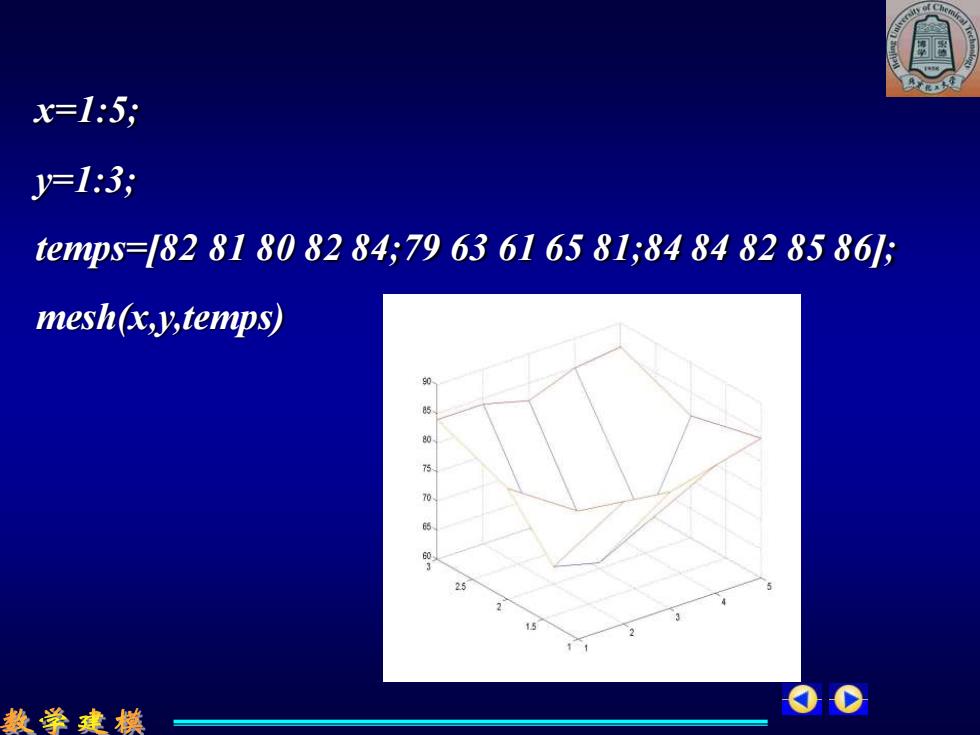
x=1:5; J=1:3; teps=82818082847963616581;8484828586]5 mesh(x,y,temps) 款学建模
x=1:5; y=1:3; temps=[82 81 80 82 84;79 63 61 65 81;84 84 82 85 86]; mesh(x,y,temps)
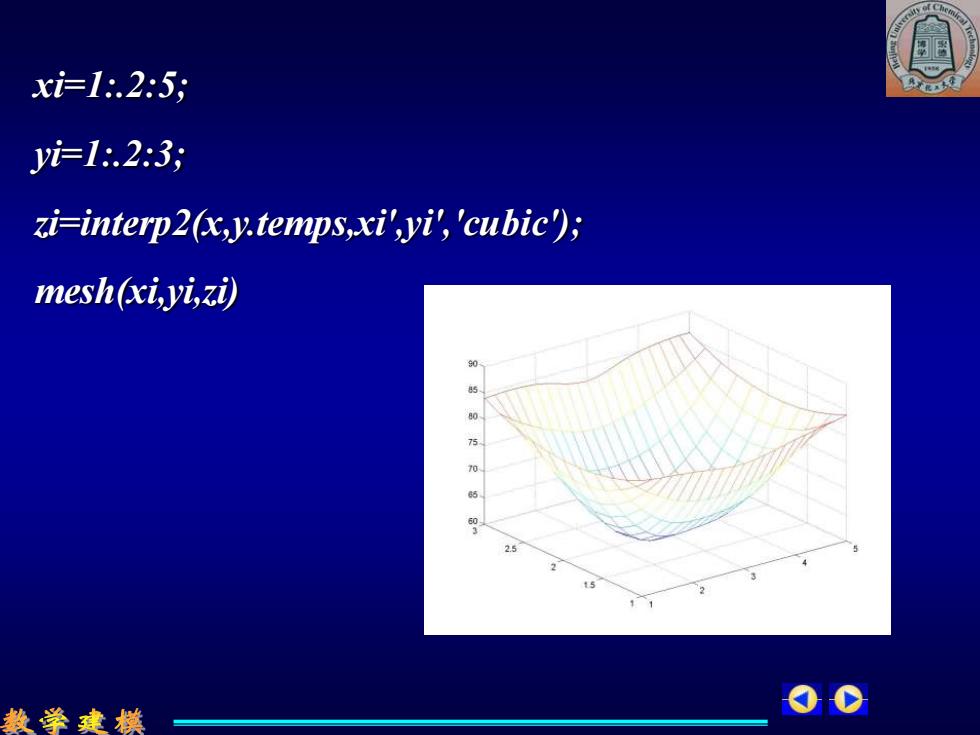
xi=1.25; Jyi12:3; zi=interp2(x,y.temps,xi,yi,'cubic); mesh(xi,yi,zi) 数学建模 00
xi=1:.2:5; yi=1:.2:3; zi=interp2(x,y.temps,xi',yi','cubic'); mesh(xi,yi,zi)

例:在某海域测得一些点(x,y)处的水深z,由下表给 出,在矩形区域(75,200)X(一50,150)内画出海 迪曲面的图形。 129 140 103.5 88 185.5 195 105.5 157.5 107.577 81 162 162 117.5 7.5 141.5 23 147 22.5 137.5 85.5 -6.5 -81 3 56.5 -66.5 84 -33.5 6 6 8 0 9 款学建模
例:在某海域测得一些点(x,y)处的水深z,由下表给 出,在矩形区域(75,200)×(-50,150)内画出海 迪曲面的图形。 x 129 140 103.5 88 185.5 195 105.5 157.5 107.5 77 81 162 162 117.5 Y 7.5 141.5 23 147 22.5 137.5 85.5 -6.5 -81 3 56.5 -66.5 84 -33.5 z 4 8 6 8 6 8 8 9 9 8 8 9 4 9