
北京化工大学2007—2008学年第二学期 《高等数学(下)》(经管类)期末考试试卷 课程代码MAT1381T 班级: 姓名: 学号: 分数: 题号 三 四 五 总分 得分 一、填空(3分×6=18分) 器 2.与向量à={2,-1,2}共线且满足a.子=-18的向量产= 3.交换积分次序d,f,r= 4.己知级数 白2n- x,则收敛半径为R 5.微分方程cos2ydr+cos2xy=0的通解是 6.差分方程2ym+1-yn=n+2满足初始条件%=4的特解为_ 二、计算题(20分) 1.(7分)计算由曲线y=x2+1,直线x+y=3以及二坐标轴所围图形面积。 经管类第1页
经管类 第 1 页 北京化工大学 2007——2008 学年第二学期 《高等数学(下)》(经管类)期末考试试卷 课程代码 M A T 1 3 8 1 T 班级: 姓名: 学号: 分数: 题号 一 二 三 四 五 总分 得分 一、填空(3 分×6=18 分) 1. 2 0 d 1 x x + = + 。 2.与向量 a 2 , 1, 2 → = − 共线且满足 a r 18 → → = − 的向量 r → = 。 3.交换积分次序 1 0 d ( , )d y y y f x y x = 。 4.已知级数 ( ) 1 1 2 1 n n n x n = − − ,则收敛半径为 R = 。 5.微分方程 2 2 cos d cos d 0 y x x y + = 的通解是 。 6.差分方程 1 2 2 n n y y n + − = + 满足初始条件 0 y = 4 的特解为 。 二、计算题(20 分) 1.(7 分)计算由曲线 2 y x = +1 ,直线 x y + = 3 以及二坐标轴所围图形面积

之6分》求极限吗aed 3.(7分)己知两点M(4,√2,1和M2(3,0,2),求向量MM2的模、方向余弦以 及与M,M,平行的单位向量。 三、计算题(7分×4=28分) 1.己知隐函数z=f(x,y)是由方程e=xyz确定的,求dz。 经管类第2页
经管类 第 2 页 2.(6 分)求极限 2 0 0 1 lim arctg d x x t t → x 3.(7 分)已知两点 M1 (4 , 2 ,1) 和 M2 (3 , 0 , 2) ,求向量 M M1 2 ⎯⎯⎯⎯→ 的模、方向余弦以 及与 M M1 2 ⎯⎯⎯⎯→ 平行的单位向量。 三、计算题(7 分×4=28 分) 1.已知隐函数 z f x y = ( , ) 是由方程 e z = x yz 确定的,求 dz

2.函数:=fxy,x+),且f具有二阶连续偏导数,求,”。 3.设函数f(x,y)=xy-x2-y2-2x-2y+4定义在整个实平面上,求f(x,y)的极值。 4.计算二重积分x-1drdy,其中D由四条直线x=0,x=2,y=l,y=0所 围成的平面区域。 经管类第3页
经管类 第 3 页 2.函数 z f x y x y = + ( , ) ,且 f 具有二阶连续偏导数,求 ' x z , '' xy z 。 3.设函数 2 2 f x y x y x y x y ( , ) 2 2 4 = − − − − + 定义在整个实平面上,求 f x y ( , ) 的极值。 4.计算二重积分 1 d d D x y x y − ,其中 D 由四条直线 x = 0 ,x = 2, y = 1, y = 0 所 围成的平面区域

四、解答题(6分×4=24分) 1.讨论级数元00的敛散性. n 2.求级数∑(+)x的收敛域以及它在收敛域内的和函数。 经管类第4页
经管类 第 4 页 四、解答题(6 分×4=24 分) 1.讨论级数 1 cosn n n = 的敛散性。 2.求级数 ( ) 1 0 1 n n n x + = + 的收敛域以及它在收敛域内的和函数
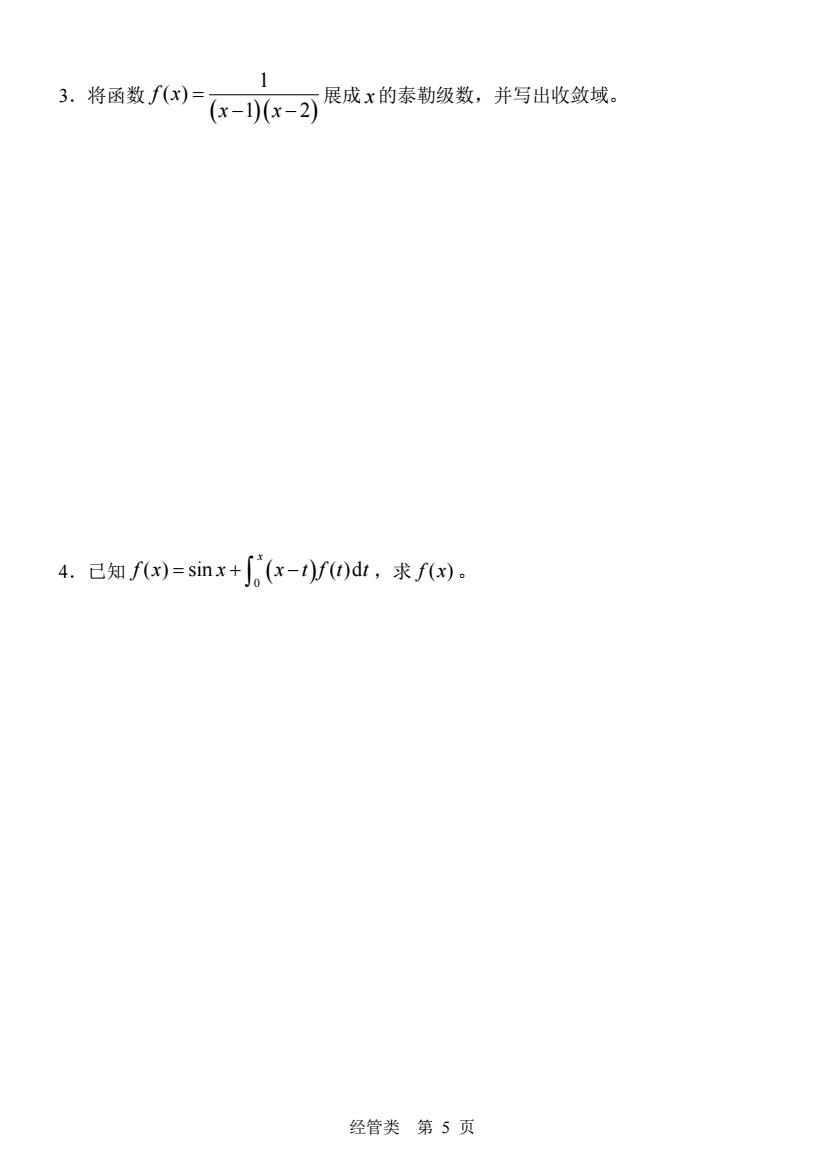
3。将画函数心)K-g-2展成x的泰勒级数,并写出收敛线。 4.已知fx)=sinx+∫(x-tf0)d,求fx)。 经管类第5页
经管类 第 5 页 3.将函数 ( )( ) 1 ( ) 1 2 f x x x = − − 展成 x 的泰勒级数,并写出收敛域。 4.已知 ( ) 0 ( ) sin ( )d x f x x x t f t t = + − ,求 f x( )

五、(5分×2=10分) 1.某公司每年工资总额在比前一年增加20%的基础上再追加200万元。若以y,表示 第n年的工资总额(单位:百万元),求y,满足的方程:若2000年该公司的工资总额 1000万元,则4年后工资总额将是多少? 2.设fx)在[0,上可导,且∫x)dr=0。 试证:(1)在(0,)内至少有一点5,使∫。f(x)dx=-5∫(5): (2)在(0,1)内至少有一点n,使2f()+nf'(7=0。 经管类第6页
经管类 第 6 页 五、(5 分×2=10 分) 1.某公司每年工资总额在比前一年增加 20%的基础上再追加 200 万元。若以 n y 表示 第 n 年的工资总额(单位:百万元),求 n y 满足的方程;若 2000 年该公司的工资总额 1000 万元,则 4 年后工资总额将是多少? 2.设 f x( ) 在 0 ,1 上可导,且 1 0 f x x ( )d 0 = 。 试证:(1)在 (0 ,1) 内至少有一点 ,使 ( ) 0 f x x f ( )d = − ; (2)在 (0 ,1) 内至少有一点 ,使 2 0 f f ( ) + = '( )