
北京化工大学2008—2009学年第二学期 《高等数学》(经管类)期末考试试卷 课程代码MAT13801T 班级: 姓名: 学号: 分数: 题号 二 三 多 总分 得分 一、填空(3分×618分》 2.设a=+3k,方=j+3呢,则(-2à)36= 3.交换二次积分顺序:∫d,f,列d= 4.已知级数2”,其收敛半径R=」 el 3% 5.已知二阶线性常系数齐次常微分方程的特征根为-2和3,则此常微分方程是 6.差分方程y+2+5y41+6y=0的通解为 二、解答题(6分X7=42分) x-∫efd 1.求osin2x 第1页
第 1 页 北京化工大学 2008——2009 学年第二学期 《高等数学》(经管类)期末考试试卷 课程代码 M A T 1 3 8 0 1 T 班级: 姓名: 学号: 分数: 题号 一 二 三 四 总分 得分 一、填空(3 分×6=18 分) 1. 2 0 d 1 x x + = + 。 2.设 a i k 3 → → → = + , b j k 3 → → → = + ,则 ( 2 ) 3 a b → → − = 。 3.交换二次积分顺序: ( ) 1 0 d , d y y y f x y x = 。 4.已知级数 1 1 3 n n n n x − = ,其收敛半径 R = 。 5.已知二阶线性常系数齐次常微分方程的特征根为-2 和 3,则此常微分方程是 。 6.差分方程 2 1 5 6 0 x x x y y y + + + + = 的通解为 。 二、解答题(6 分×7= 42 分) 1.求 2 0 2 0 e d lim sin 2 x t x x t → x x −
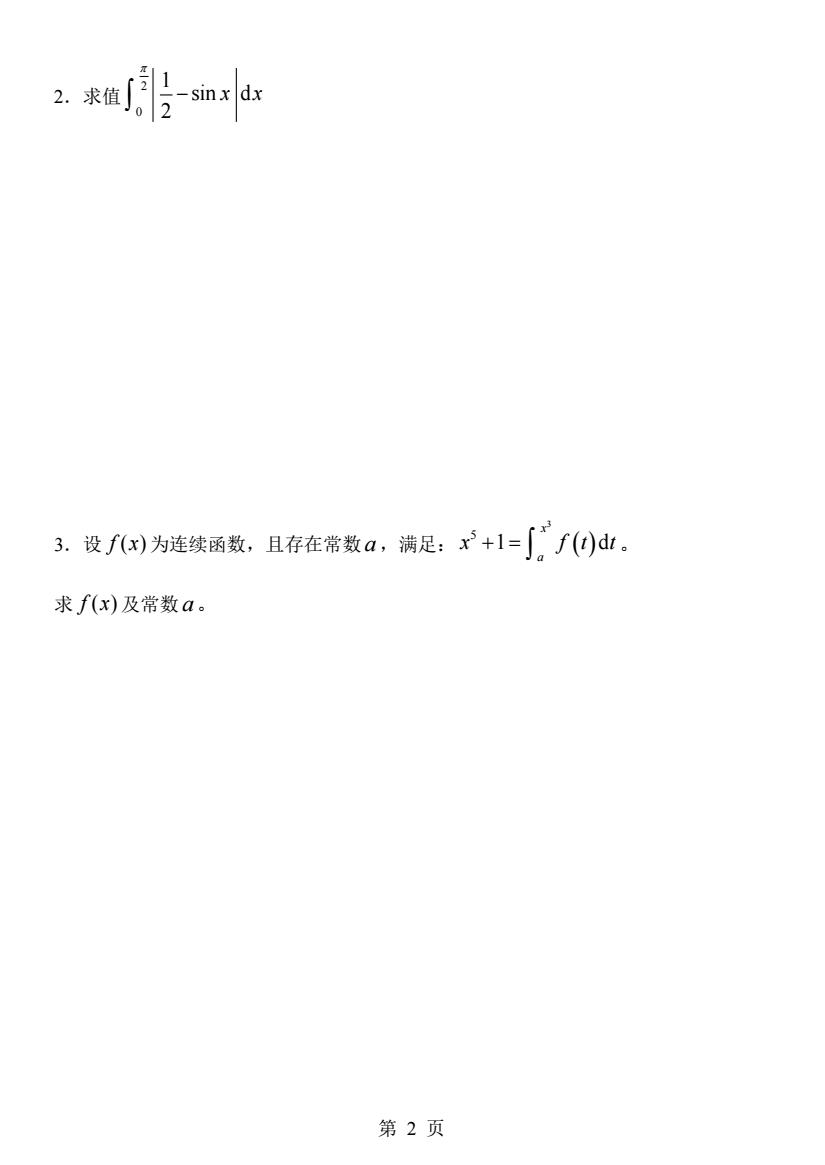
2.求值}mxdr 3.设f)为连续函数,且存在常数a,满足:x+l=∫f)d。 求f(x)及常数a。 第2页
第 2 页 2.求值 2 0 1 sin d 2 x x − 3.设 f x( ) 为连续函数,且存在常数 a ,满足: ( ) 3 5 1 d x a x f t t + = 。 求 f x( ) 及常数 a

4.设可微商数:=收,列上-加能,求积。 5.设z=f(xy,x+y),f具有二阶连续导数,求,”· 第3页
第 3 页 4.设可微函数 z z x y = ( , ) 由 ln y z z x = 确定,求 z x 。 5.设 z f x y x y = + ( , ) , f 具有二阶连续导数,求 ' x z , '' xy z

6.计算二重积分∬sin+ydo,其中D={《x,y川x2≤x+y≤4π}。 7.求函数f(x,y)=-x3+y3-3y的极值。 第4页
第 4 页 6.计算二重积分 2 2 sin d D x y + ,其中 ( ) 2 2 2 2 D x y x y = + , 4 。 7.求函数 ( ) 3 3 f x y x y xy , 3 = − + − 的极值

三、解答题(6分×5=30分) 5ncos2r 1.判断级数 2” 的敛散性。 2.将/闭)一2x一3展开成x的幂级数,并写出展开式的成立区间。 第5页
第 5 页 三、解答题(6 分×5=30 分) 1.判断级数 2 1 cos 3 2 n n n n = 的敛散性。 2.将 2 1 ( ) 2 3 f x x x = − − 展开成 x 的幂级数,并写出展开式的成立区间

3.设级数为 n ,求其收敛域及其在收敛域上的和函数。 第6页
第 6 页 3.设级数为 1 n n x n = ,求其收敛域及其在收敛域上的和函数

4.求y"-6y'+9y=e的通解。 5.在某产品的生产中,1时期产品的价格P决定着生产者在下一时期愿意提供给市场 的供给量S,还决定着本期该产品的需求量D,因此有: D,=1-4P,S,=-3+2P- 求供需平衡(即D,=S,)时价格P,随时间的变化规律。(设t=0时,==1) 第7页
第 7 页 4.求 '' ' 6 9 ex y y y − + = 的通解。 5.在某产品的生产中, t 时期产品的价格 Pt 决定着生产者在下一时期愿意提供给市场 的供给量 t 1 S + ,还决定着本期该产品的需求量 Dt ,因此有: 1 4 D P t t = − , 1 3 2 t t S P = − + − 求供需平衡(即 D S t t = )时价格 Pt 随时间的变化规律。(设 t = 0 时, 0 0 1 t t P P = = = )

四、(5分×2=10分) 1.设n为正整数,证明方程x”+nx-1=0存在唯一正实根xm,并证明当a>1时, 三女收敛 2.设F(x)=f(x)g(x),其中可微函数f(x)、g(x)在(-o0,+∞)内满足以下条件 f(x)=g(x),g'(x)=f(x),且f(0)=0,f(x)+g(x)=2e (1)求F(x)所满足的一阶微分方程: (2)求出F(x)的表达式。 第8页
第 8 页 四、(5 分×2=10 分) 1.设 n 为正整数,证明方程 1 0 n x nx + − = 存在唯一正实根 n x ,并证明当 1 时, 1 n n x = 收敛。 2.设 F x f x g x ( ) ( ) ( ) = ,其中可微函数 f x( ) 、 g x( ) 在 (− + , ) 内满足以下条件: f x g x '( ) ( ) = , g x f x '( ) ( ) = ,且 f (0 0 ) = , ( ) ( ) 2ex f x g x + = (1)求 F x( ) 所满足的一阶微分方程; (2)求出 F x( ) 的表达式