
北京化工大学2009—2010学年第一学期 《高等数学(I)》期末考试试卷 课程代码MAT13900T 班级: 姓名: 学号: 分数: 题号 二 5 总分 4 得分 一、填空(3分×6=18分) 1<1 1.设f(x)= 0其他 gx)=e,则f[g(x= 2.设y=enm6,则d 3.求曲面x2+)y2+2=1与曲面:=√2+y的交线在x0y面上的投影曲线方程为 dx 1 4.已知d,则n 5.过原点和点(3,-1,2)的直线方程为 6.由点A1,1,1),B(-1,1,2)和C(1,0,2)所构成的三角形的面积 第1页
第 1 页 北京化工大学 2009——2010 学年第一学期 《高等数学(I)》期末考试试卷 课程代码 M A T 1 3 9 0 0 T 班级: 姓名: 学号: 分数: 题号 一 二 三 总分 1 2 3 4 5 得分 一、填空(3 分×6=18 分) 1.设 1 1 ( ) 0 x f x = 其他 , ( ) ex g x = ,则 f g x ( ) = 。 2.设 arctan e x y = ,则 1 d x y = = 。 3.求曲面 2 2 2 x y z + + =1 与曲面 2 2 z x y = + 的交线在 xO y 面上的投影曲线方程为 。 4.已知 d 1 d ' x y y = ,则 2 2 d d x y = 。 5.过原点和点 (3, 1, 2 − ) 的直线方程为 。 6.由点 A(1,1,1), B(−1,1, 2) 和 C(1, 0 2, ) 所构成的三角形的面积
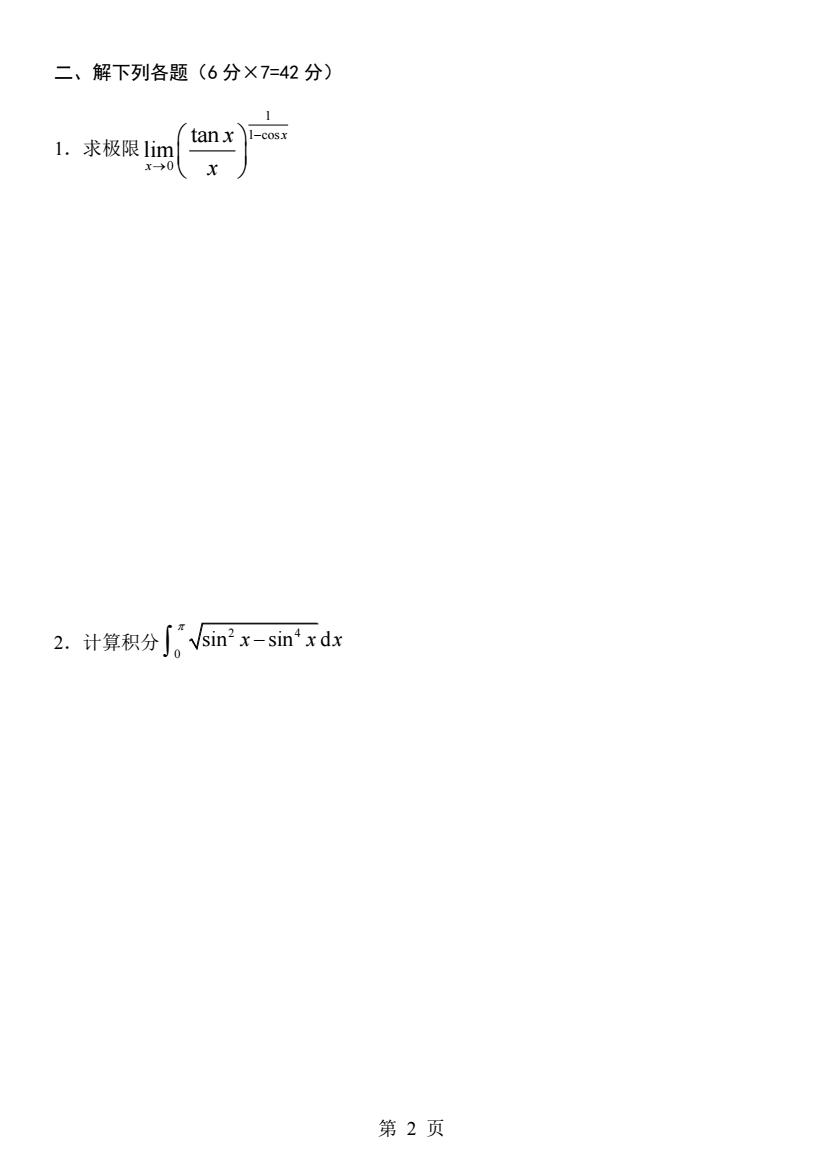
二、解下列各题(6分×7=42分) 1求极限 tanxi-cosx 2.计算积分∫。VSin'x-sin'xdx 第2页
第 2 页 二、解下列各题(6 分×7=42 分) 1.求极限 1 1 cos 0 tan lim x x x x − → 2.计算积分 2 4 0 sin sin d x x x −

3.证明:∫。x(-x)”dr=∫。x(-x)”dr 4.设曲线方程为y=∫sVB-Fd山 求:(1)曲线方程的定义域:(2)求曲线在定义域内的全长。 第3页
第 3 页 3.证明: ( ) ( ) 1 1 0 0 1 d d 1 m n n m x x x x − x = − x 4.设曲线方程为 2 3 3 d x y t t − = − , 求:(1)曲线方程的定义域;(2)求曲线在定义域内的全长

r+2x+号 -1≤x<0 5.设f(x)= ex 0≤x≤1 (e'+1) 求F(x)=∫f()dl的表达式,并讨论F(x)在定义域上的连续性。 6.造一圆柱形封闭油罐,已知体积为100m3,问油罐半径为多少时,所用材料最省。 第4页
第 4 页 5.设 ( ) 2 2 3 1 2 , 1 0 2 4 ( ) e , 0 1 e 1 x x x x x f x x + + − = + 求 ( ) 1 ( ) d x F x f t t − = 的表达式,并讨论 F x( ) 在定义域上的连续性。 6.造一圆柱形封闭油罐,已知体积为 100m3,问油罐半径为多少时,所用材料最省
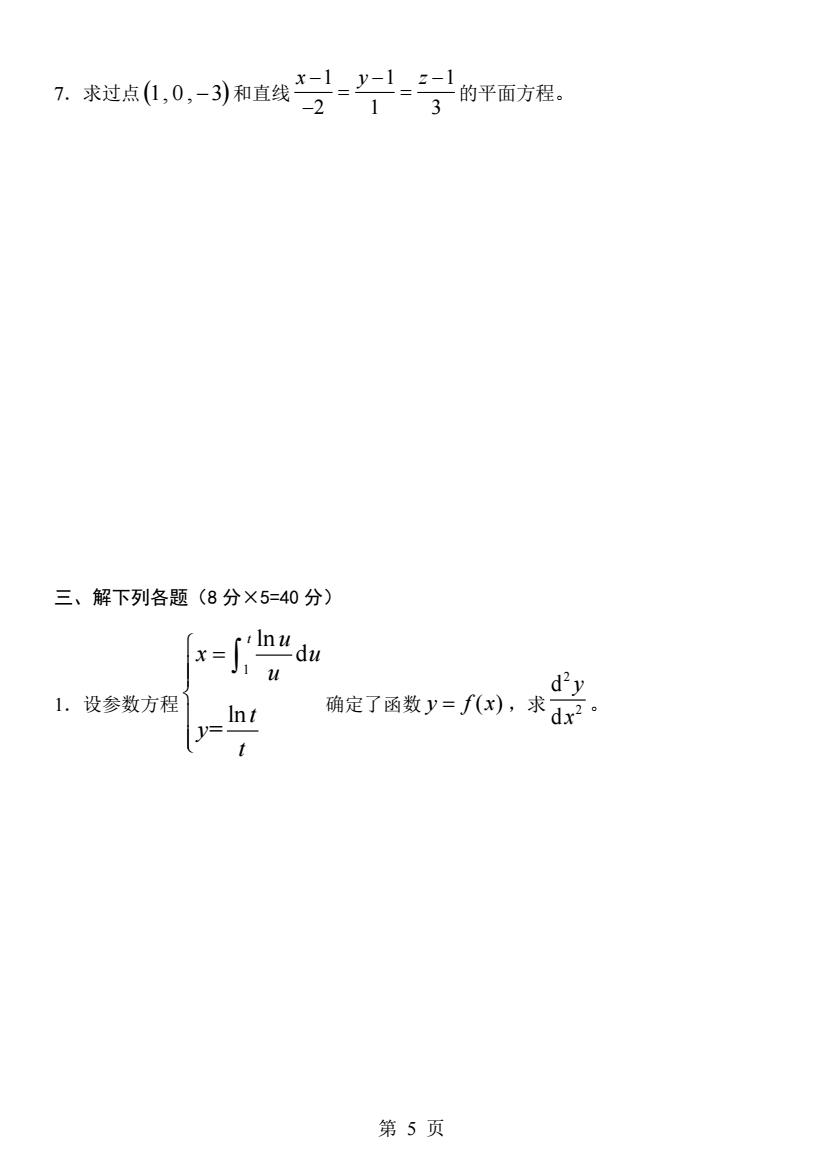
1求滋点,0,)和直袋号的平面方视。 三、解下列各题(8分×5=40分) 手-g d2y 1.设参数方程】 Int 确定了函数y=fx),求d, t 第5页
第 5 页 7.求过点 (1, 0 , 3 − ) 和直线 1 1 1 2 1 3 x y z − − − = = − 的平面方程。 三、解下列各题(8 分×5=40 分) 1.设参数方程 1 ln d ln = t u x u u t y t = 确定了函数 y f x = ( ) ,求 2 2 d d y x

2.证明:当x>0时,x2+1>nx 3.求曲线y=lnx,y=0,x=1,x=e所围成图形绕y轴旋转一周所形成的旋转体 的体积。 第6页
第 6 页 2.证明:当 x 0 时, 2 x x + 1 ln 。 3.求曲线 y x = ln ,y = 0, x =1,x = e 所围成图形绕 y 轴旋转一周所形成的旋转体 的体积

4.设一等腰梯形水闸,上底为4米,下底为10米,高为10米,下底与水面持平,水 的密度为P,重力加速度为g。求水闸每一面承受的水的压力。(不必写出压力单位》 第7页
第 7 页 4.设一等腰梯形水闸,上底为 4 米,下底为 10 米,高为 10 米,下底与水面持平,水 的密度为 ,重力加速度为 g 。求水闸每一面承受的水的压力。(不必写出压力单位)

5.设f(x)在-a,ad上有四阶连续导数(即f(x)在[-a,a上存在且连续)。求: (1)将f(x)展成带拉格朗日余项的麦克劳林公式。 2)当f(O)=f"(0)=0时,至少存在一点n∈[-a,d,使af()=60“f(x)dr。 第8页
第 8 页 5.设 f x( ) 在 −a a, 上有四阶连续导数(即 (4) f x( ) 在 −a a, 上存在且连续)。求: (1)将 f x( ) 展成带拉格朗日余项的麦克劳林公式。 (2)当 ( ) ( ) f f 0 0 = = '' 0 时,至少存在一点 − a a, ,使 ( ) 5 (4) 60 ( )d a a a f f x x − =