
09-10高数(上)期末试题 一、填空(3分×6=18分) ha时-头a时=geen 其他 2.设y=ec,则d w=2
09-10高数(上)期末试题 1 1 ( ) ( ) , ( ( )) 0 x x f x g x e f g x = = = 1.已知 , 则 其他 arctan 1 2. , x x y e dy 设 = = 则 = 一 、填空(3 6 分 =18分) 1 ( ) 1 1 0 ( ( )) 0 0 0 g x x f g x x = = 其他 arctan 1 1 1 2 x dy e dx x x = + 4 1 1 4 x dy e dx = =

3.求曲面x2+y2+2=1与曲面2=√x2+y2的交线在 xOy面上的投影曲线方程为 =+y 消去Ξ得x2+y2+x2+y2=1 x2+y2+z2=1 投影方程为:
2 2 2 2 2 3. 1 x y z z x y xOy 求曲面 + + = = + 与曲面 的交线在 面上的投影曲线方程为 2 2 1 2 0 x y z + = = 投影方程为: 2 2 2 2 2 2 2 2 2 1 1 z x y z x y x y x y z = + + + + = + + = 消去 得

4.已知 d'x d'x=-yd=-y 5.过原点和点(3,-1,2)的直线方程为 所求直线的方向向量为3,-1,2) 所求直线方程为行子月
2 2 1 4 dx d x dy y dy = = .已知 ,则 5.过原点和点(3,-1,2)的直线方程为 2 2 2 3 ( ) d x y dx y dy y y dy − = = − 所求直线的方向向量为(3, 1,2) − 3 1 2 x y z = = − 所求直线方程为

6.由点A1,1,1),B(-1,1,2)和C1,0,2)所构成的三角形面积 ABx AC= -201=i+2j+2元 0-11 w2+3-月
6.由点A B C (1,1,1), ( 1,1,2) (1,0,2) − 和 所构成的三角形面积 2 0 1 2 2 0 1 1 i j k AB AC i j k = − = + + − 1 3 222 1 2 2 2 2 ABC S = + + =
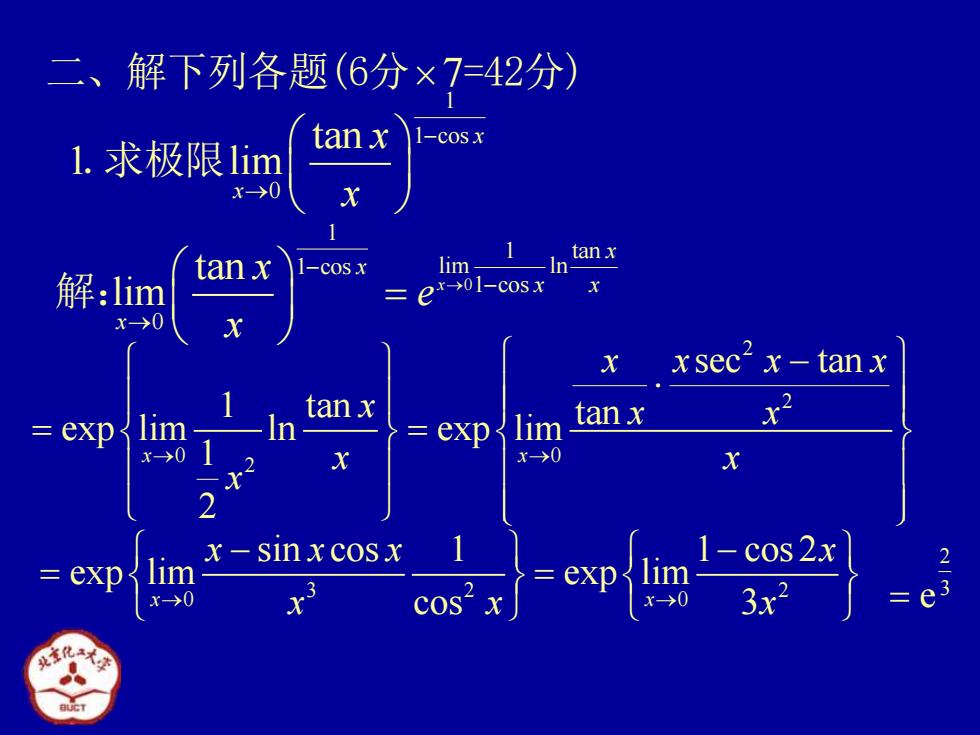
二、解下列各题(6分×7=42分) 1.求极限1im tan x x-→0 1-cosx lim- tanx In 解:lim ex-01-cosx x-→0 xsec2 x-tanx tan x explim tan x =exp lim x-→0 X→0 x-sinxcosx 1-cos2x exp 2- x→0 cos 0 3x2 =e3
二、解下列各题(6分7=42分) 1 1 cos 0 tan 1 lim x x x x − → .求极限 0 1 1 tan 1 cos lim ln 1 cos 0 tan lim x x x x x x x e x → − − → = 解: 2 2 0 0 2 sec tan 1 tan tan exp lim ln exp lim 1 2 x x x x x x x x x x x x → → − = = 3 2 0 sin cos 1 exp lim cos x x x x → x x − = 2 0 1 cos 2 exp lim x 3 x → x − = 2 3 = e

2.计算积分Vsin2x-sinxdx :sin x-sin'xd sinxeos -sinxcossinxeos
2 4 0 sin sin x xdx − 2.计算积分 2 4 0 0 sin sin sin cos x xdx x x dx − = 解: 2 0 2 sin cos sin cos x xdx x xdx = − 2 2 2 0 2 1 1 sin sin 1 2 2 x x =−=
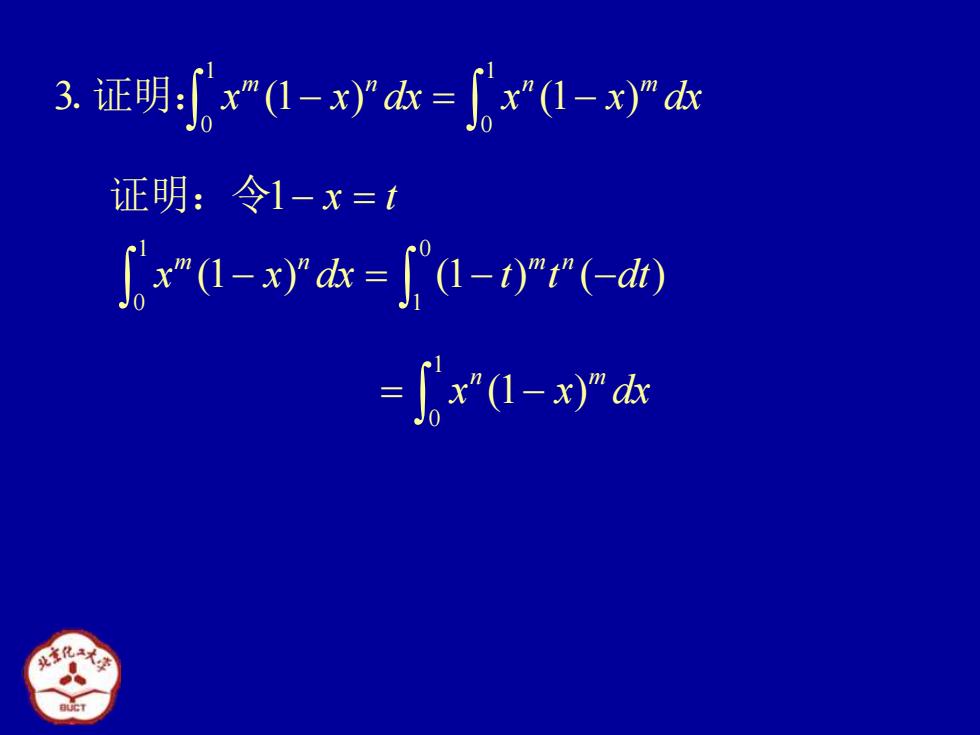
3.证明x0-xr本=x0-xk 证明:令1-x=t [x"(-x)"&=f"A-P(-d) =∫x-x
1 1 0 0 3 (1 ) (1 ) m n n m x x dx x x dx − = − .证明: 证明:令1− = x t 1 0 (1 ) n m = − x x dx 1 0 0 1 (1 ) (1 ) ( ) m n m n x x dx t t dt − = − −

4.设曲线方程为y=6V3-iFd山,求(1)曲线方程的 定义域:(2)求曲线在定义域内的全长 解3-2≥0,定义域为-√3V]y'=V3-x L=+y产&=+3-x =2sinl 22cos12cosid -40+os2a=40+5n2 4π 3
2 3 3 , 1 2 x y t dt − = − 4.设曲线方程为 求( )曲线方程的 定义域;( )求曲线在定义域内的全长 2 解:3 0, − t 定义域为[ 3 3] − , 3 2 3 L y dx 1 − = + 3 2 3 1 3 x dx − = + − 3 0 x t t tdt 2sin 2 2cos 2cos = 3 0 4 (1 cos 2 )t dt = + 3 0 1 4( sin 2 ) 2 t t = + 4 3 3 = + 2 y x = −3

+2x -1≤x<0 5.设f(x) 三 ,求F(x)=J/)d 0≤x≤1 的表达式,并讨论F(x)在定义域上的连续性。 解:当-1≤x<0时, Po=0t--2a+3=++ 当0≤x≤时, 四=r*2w+ein-g
2 1 2 3 1 2 , 1 0 2 4 ( ) , ( ) ( ) , 0 1 ( 1) ( ) x x x x x x f x F x f t dt e x e F x − + + − = = + 5.设 求 的表达式,并讨论 在定义域上的连续性。 解:当− 1 0 x 时, 2 1 1 3 1 ( ) ( ) ( 2 ) 2 4 x x F x f t dt t t dt − − = = + + 1 1 1 3 2 2 4 4 = + + − x x x 当0 x 1时, 0 2 2 1 0 3 1 ( ) ( 2 ) 2 4 ( 1) t x t e F x t t dt dt e − = + + + + 1 1 4 1 x e = − +

+x2+ 4 0≤x≤1 ex +1 在x=0处 F)=F=FO=-子 x->0 x->0 F(x)在[-1,1]连续
在x = 0处 - 0 0 1 lim ( ) lim ( ) (0) x x 4 F x F x F → → + = = = − F x( )在[-1,1]连续 1 1 1 3 2 , 1 0 2 4 4 ( ) 1 1 , 0 1 4 1 x x x x x F x x e + + − − = − +