
09-10高数(上) 期中试题 一、填空(3分×26=78分) 1.设f(x)的定义域D=[0,1],函数f(x)+f(x-a) (0<a<1)的定义域为 [a,1] a≤x≤1+a 2.设f(x)=e,fo(x】=1-x,则p(x)= f[o(x)]=e""()=1-x p3(x)=ln(1-x) p(x)=1n1-x)x<1
09-10高数(上)期中试题 2 [0,1], ( ) ( ) (0 1) f x D = f x f x - a a + 1.设 ( )的定义域 函数 的定义域为 ( ) 3 ( ) , [ ( )] 1 , x 2.设f x e f x x x = = − = 则 一 、填空(3 26 8 分 =7 分) 2 0 1 0 1 x a x − 1 + , 1 1 a x a x − [ 1] a, 3 ( ) [ ( )] 1 x f x e x = = − 3 ( ) ln(1 ) x x = − 3 ( ) ln(1 ) 1 x x x = −
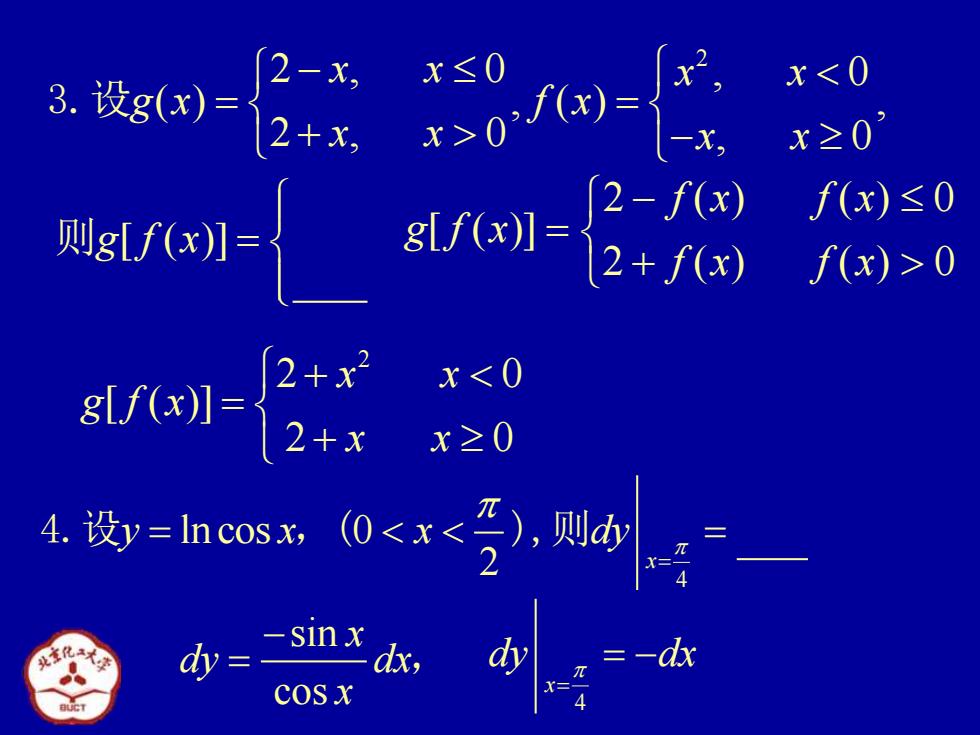
3.设g(x)= 2-x, x≤0 x0 x<0 x≥0 4.设y=ncas0<x<孕.则 X= -sinx dy dx, dy =-d COSx
4 ln cos 0 2 x y x x dy = 4.设 = = ,( ),则 2 2 , 0 , 0 ( ) , ( ) , 2 , 0 , 0 x x x x g x f x x x x x − = = + − 3.设 g f x [ ( )] = 则 2 ( ) ( ) 0 [ ( )] 2 ( ) ( ) 0 f x f x g f x f x f x − = + 2 2 0 [ ( )] 2 0 x x g f x x x + = + sin cos x dy dx x − = , 4 x dy dx = = −

5.设y=arctan(e),则y"(O)= y'= e=e0+e-2ee e y(0)=0 (1+e2x)2 8已知方西=1+心确定函数=则会。- e2 y=e'+xe'yy= 1-xe" 当x=0时,y=1 y'(0)=e
5 arctan( ) (0) x .设y e y = = ,则 2 2 2 2 2 (1 ) 2 , 1 (1 ) x x x x x x x e e e e e y y e e + − = = + + y (0) 0 = 0 1 ( ), y x dy y xe y y x dx = + = = = 6.已知方程 确定函数 则 当x y = = 0 , 1 时 y y y e xe y = + y e (0) = 1 y y e y xe = −
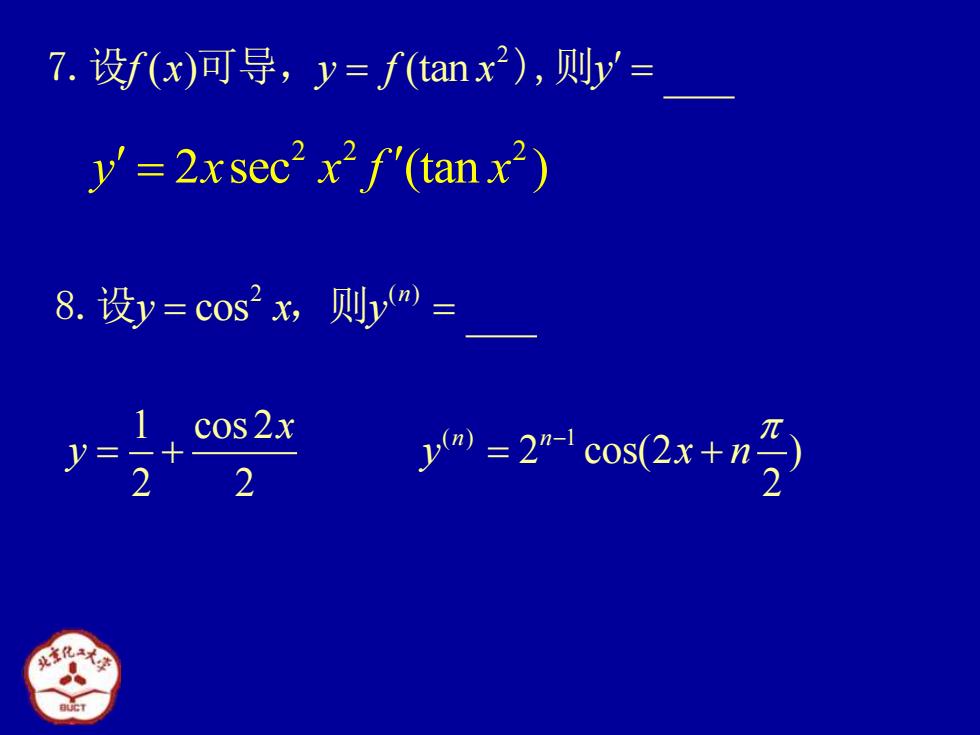
7.设fx)可导,y=fanx),则y= y'=2xsec2 x2f(tanx2) 8.设y=cos则y网= 1,cos2x 2 2cos(x
2 ( ) cos n 8.设y x y = = ,则 2 7.设f x y f x y ( ) (tan 可导, = = ),则 2 2 2 y x x f x = 2 sec (tan ) 1 cos 2 2 2 x y = + ( ) 1 2 cos(2 ) 2 n n y x n − = +

9.曲线 二co2布=处的切线方程 y=sint dx dt =-2sin 2t, dt dy cost dx -2sin 2t 4sint 2 4 (x-0 √W2x+4y-22=0
2x y + − = 4 2 2 0 cos 2 sin 4 x t t y t = = = 9.曲线 在 处的切线方程 2sin 2 , cos , dx dy t t dt dt = − = 4 2 t 4 dy dx = = − cos 1 , 2sin 2 4sin dy t dx t t = = − − 2 , 0, 2 t = x y 4 = = 2 2 ( 0) 2 4 y x − = − −
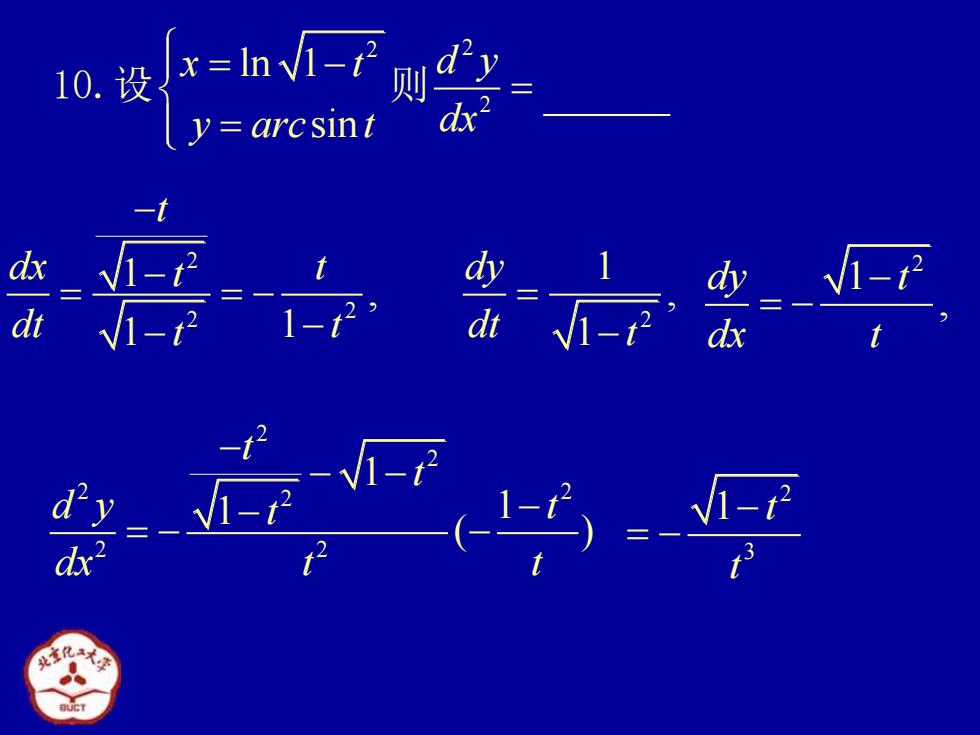
dx d 2
2 3 1 t t − = − 2 2 2 ln 1 sin x t d y y arc t dx = − = = 10.设 则 2 2 2 2 1 1 , , 1 1 1 t dx t dy t dt t dt t t − − = = − = − − − 2 2 2 2 2 2 2 1 1 1 ( ) t t d y t t dx t t − − − − − = − − 2 1 , dy t dx t − = −

1.设断)=如xa=,则= du -西.-道.1 xsec2x-tanx 1 du dx du dx du x2 2x dx xsec-x-tan x 2x3 12.极限1 msinx·arctan上=0 x→0 X 有界变量与无穷小的乘积为无穷小
2 tan ( ) , x df f x u x x du 11.设 = = ,则 = df df dx df 1 du dx du dx du dx = = 0 1 limsin arctan x x → x 12.极限 = 有界变量与无穷小的乘积为无穷小 2 2 sec tan 1 2 x x x x x − = 2 3 sec tan 2 x x x x − = 0
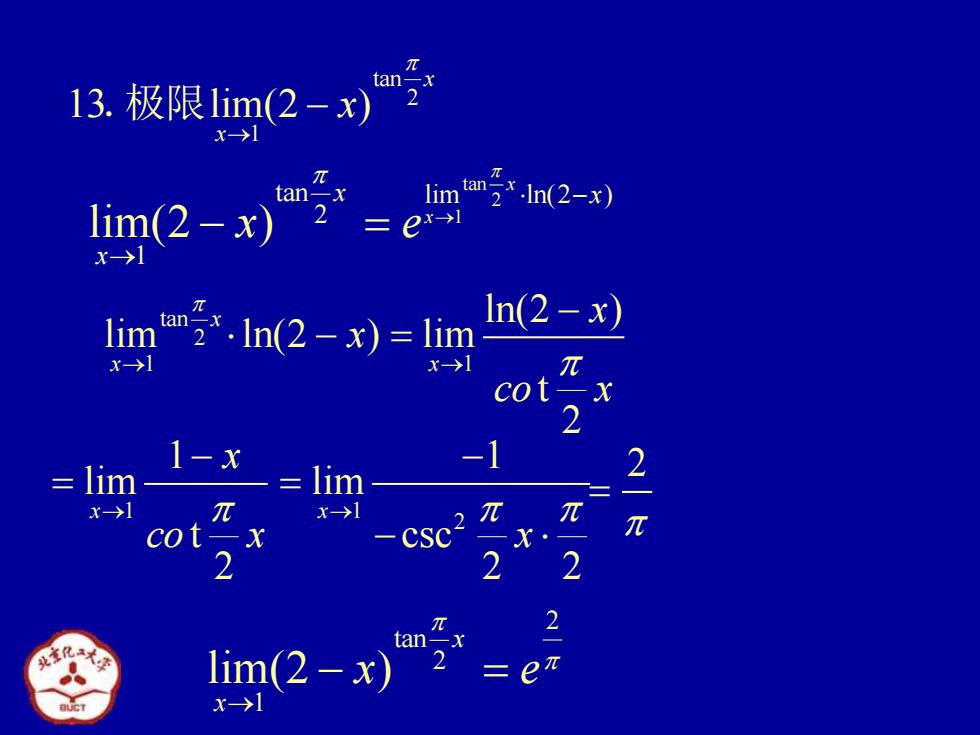
π 13.极限1im(2-x) x→1 π tan X 2-x) limtan2*.In(2-x) 2”=e limm吃x-ln(2-x)=lim n(2-x) x>1 x→1 π cotx 2 1-x -1 lim lim x-→1 x>] 2 cot-x 一X· π 2 π 2 tan lim(2-x) 2 =eπ x→1
tan 2 1 13 lim(2 ) x x x → .极限 − tan 2 1 tan lim ln(2 ) 2 1 lim(2 ) x x x x x x e → − → − = tan 2 1 1 ln(2 ) lim ln(2 ) lim t 2 x x x x x co x → → − − = 1 1 2 1 1 lim lim t csc 2 2 2 x x x co x x → → − − = = − 2 = 2 tan 2 1 lim(2 ) x x x e → − =

14.极限1im 0+x2-1 x→0 1-cosx lim 1+x2-1 1x2 lim n 2 x→0 1-cosx →0 n 2 15.极限lim x-sinx *In(1+x).tanx x-sInx lim x-sInx 1-cosx lim =lim x In(1+x).tanx x-→0 x.x2 x→0 3x2 sin x lim x>0 6x 6
1 2 0 (1 ) 1 14 lim 1 cos n x x → x + − = − .极限 1 2 2 0 0 2 1 (1 ) 1 lim lim 1 cos 1 2 n x x x x n x x → → + − = − 2 n = 2 0 sin 15 lim x ln(1 ) tan x x → x x − = + .极限 2 2 0 0 sin sin lim lim x x ln(1 ) tan x x x x → → x x x x − − = + 2 0 1 cos lim x 3 x → x − = 0 sin 1 lim x 6 6 x → x = =

16.设y=f(x)在x=0处可导,f(0)=0,则1im f(x) )=lim(()=(0) x→0 x-0 17极限1im arctan x arctanx lim xIn arctan x lim π =e x-→+o∞ arctan x mxn arctanx lim 元 元 x→+o∞ 2 1 X 2 2 arctan xπl+x2 2 lim X→+00 元 原式=e月
0 ( ) ( ) 0 (0) 0, lim x f x y f x x f → x 16.设 = = = = 在 处可导, 则 0 0 ( ) ( ) (0) lim lim (0) x x 0 f x f x f f → → x x − = = − 2 17. lim arctan x x x →+ = 极限 2 2 lim ln arctan lim arctan x x x x x x e →+ →+ = 2 ln arctan 2 lim ln arctan lim x x 1 x x x x →+ →+ = 2 2 2 1 2arctan 1 limx 1 x x x →+ + = − 2 = − 2 e − 原式 =