
08-09高数(上)期末试题 一、填空(3分×7=21分) 1.已w)=十x则V) 1+x ff(x)=1+f) x+1 1 x+2 1+x 2.设f(x)=(arctanx)2,则f'(①=
08-09高数(上)期末试题 1 ( ) , ( ( )) 1 f x f f x x = = + 1.已知 则 2 2. ( ) (arctan ) , (1) 设f x x f = = 则 一 、填空(3 7 1 分 =2 分) 1 1 1 ( ( )) 1 ( ) 2 1 1 1 x f f x f x x x + = = = + + + + 2 1 ( ) 2arctan , 1 f x x x = + (1) 4 f =

3.过点(2,0,-3)且与直线 x+y+2z-7=0 垂直的 3x+y+z=0 平面方程 所求平面方程的法向量n=1 12={-1,5,-2 311 所求平面方程为:-(x-2)+5y-0)-2(z+3)=0 即:x-5y+2z+4=0
2 - 7 0 2 0 3 3 0 x y z x y z + + = + + = 3.过点( ,,- )且与直线 垂直的 平面方程 1 1 2 { 1,5, 2} 3 1 1 i j k 所求平面方程的法向量n = = − − 即:x y z − + + = 5 2 4 0 所求平面方程为:-( 2) 5( 0) 2( 3) 0 x y z − + − − + =

4.曲面z=x2+y2与平面x+y+z=1的交线在xOy面上的 投影方程 z=x2+y2 消去z得x2+y2-1+x+y=0 X+y+2=1 拟影方为++0+分- 2=0 s)月 x→0 { -1-x lim e-1-x x(e-1) x->0 x2 ex-11 lim x-→0 2x 2
2 2 4 1 .曲面z x y x y z xOy = + + + = 与平面 的交线在 面上的 投影方程 0 1 1 5 lim 1 x x→ x e − = − . 2 2 2 2 1 0 1 z x y z x y x y x y z = + + − + + = + + = 消去 得 1 1 3 2 2 ( ) ( ) 2 2 2 0 x y z + + + = = 投影方程为 2 0 0 0 1 1 1 1 lim lim lim 1 ( 1) x x x x x x x e x e x → → → x e x e x − − − − − = = − − 0 1 1 lim 2 2 x x e → x − = =
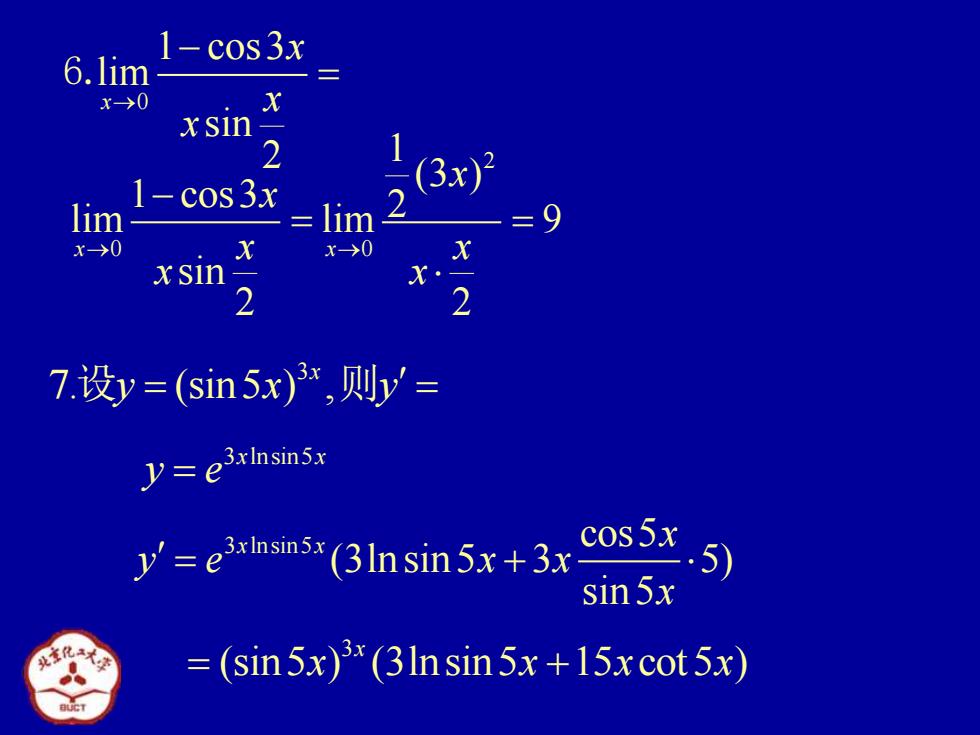
6.lim 1-cos3x x-→>0 xsin- 1-cos3x (3x)月 lim lim -→0 x→0 xsin 2 7设y=(sin5x),则y'= =e3xInsin5x =exnsins*(3In sin5x+3x cos5x 5 sin5x =(sin5x)*(3Insin5x+15xcot 5x)
0 1 cos3 lim sin 2 x x x x → − 6. = 3 7. (sin5 ) , x 设y x y = = 则 2 0 0 1 (3 ) 1 cos3 2 lim lim 9 sin 2 2 x x x x x x x x → → − = = 3 lnsin5 x x y e = 3 lnsin5 cos5 (3ln sin 5 3 5) sin 5 x x x y e x x x = + 3 (sin5 ) (3lnsin5 15 cot 5 ) x = + x x x x

二、解下列各题(6分×6=36分) 1.设y=cos”xsinn,求d 解:y=ncosx(-sinx)sinx+cos”xcosnxn ncos"x.cos(n+1)x dy =[ncos"x.cos(n+1)x]dx
二、解下列各题(6分6=36分) 1 cos sin , n .设y x nx dy = 求 1 cos ( sin ) sin cos cos n n y n x x nx x nx n − 解: = − + 1 cos cos( 1) n n x n x − = + 1 [ cos cos( 1) ] n dy n x n x dx − = +

2.已知f(x)=5-2,求f(x)的间断点,并对间断点作出分类 x=2是间断点 1im5-2=0 lim 5*-2 +oo 2 x-→2 x=2是第二类间断点,无穷型
1 2 ( ) 5 , ( ) , . x f x f x − 2.已知 = 求 的间断点 并对间断点作出分类 x = 2是间断点 1 2 2 lim 5 0 x x − − → = 1 2 2 lim 5x x + − → = + x = 2是第二类间断点,无穷型

rcco 3.求极限1im lim xIn -arccotx 小 arccotx X ≥lim arc cot xπ X→-0 原式=e
1 3 lim cot x x arc x →− .求极限 1 1 lim ln cot lim cot x x x arc x x arc x e →− →− = 1 ln cot 1 lim ln cot lim x x 1 arc x x arc x x →− →− = 2 2 1 1 ( ) cot 1 limx 1 arc x x x →− − + = − 1 = 1 e 原式 =

In xdx 1+Inx =t,x e"-,dx e"-.2tdt 篇房- -+ = -+lnx)2-21+nx+C
ln 1 ln xdx x x + 4. 2 2 1 1 1 ln , , 2 t t x t x e dx e tdt − − 设 + = = = 2 2 2 1 2 1 ln 1 2 2 ( 1) 1 ln t t xdx t e tdt t dt x x e t − − − = = − + 2 3 2 3 = − + t t C 3 2 2 (1 ln ) 2 1 ln 3 = + − + + x x C

5.计算[x2e2dk 2xk --咖-。-x*ea e-3+3-
1 2 2 0 x x e dx − 5.计算 1 1 1 2 2 2 2 2 2 1 2 0 0 0 0 1 1 1 2 2 2 2 x x x x x e dx x de x e e xdx − − − − = − = − + 1 1 2 2 2 2 1 2 0 0 0 1 1 1 1 1 2 2 2 2 2 x x x e xde e xe e dx − − − − − = − − = − − + 2 2 2 1 0 1 1 1 1 ( ) 2 2 2 2 x e e e − − − = − − + − 2 2 1 1 4 4 e e − − = − − + 1 5 2 4 4 e − = −

6.求曲线0=2asn20≤0≤号a>0所围成平面 图形的面积。 解: do-2asn 30d0 1=2wsm30=2如1g0
2 sin 3 , 0 , 0 3 a a = 6.求曲线 所围成平面 图形的面积。 解: 1 2 2 2 2 sin 3 2 dA d a d = = 2 2 2 3 3 0 0 1 cos6 2 sin 3 2 2 A a d a d − = = 3 2 2 0 1 1 1 2 sin 6 2 12 3 a a = − =