
北京化工大学2008—2009学年第一学期 《高等数学》(经管类)期末考试试卷 课程代码MAT13800T 班级: 姓名: 学号: 分数: 题号 三 四 总分 得分 一、填空(3分×618分) 1.已知fx)=x2,f[o(x=1-x2(xs1),则p(x)= In(cosx+v1-x2) 2.m e*+sin 2x +(1+x) 3.若曲线y=x2+x-2的一条切线与直线x+y=3平行,则该切线方程是 4设函数)y=e0,其中f)=阶可导,则 2 5.设f'(sin2x)=cos2x,f(0)=1,则f(x)=」 6.设商品的需求函数为Q=400-100P(P为价格),则P=1时的需求价格弹性是 二、计算(6分×8) 1.计算1im1+3x)面。 第1页共6页
第 1 页 共 6 页 北京化工大学 2008——2009 学年第一学期 《高等数学》(经管类)期末考试试卷 课程代码 M A T 1 3 8 0 0 T 班级: 姓名: 学号: 分数: 题号 一 二 三 四 总分 得分 一、填空(3 分×6=18 分) 1.已知 2 f x x ( ) = , 2 f x x ( ) 1= − ( x 1) ,则 ( ) x = 。 2. ( ) ( ) 2 2 1 0 ln cos 1 lim 1 e sin 2 x x x x x x x → + − + + + = 。 3.若曲线 2 y x x = + − 2 的一条切线与直线 x y + = 3 平行,则该切线方程是 。 4.设函数 ( ) e f x y − = ,其中 f x( ) 二阶可导,则 2 2 d d y x = 。 5.设 ( ) 2 2 f x ' sin x = cos , f (0) =1 ,则 f x( ) = 。 6.设商品的需求函数为 Q P = − 400 100 ( P 为价格),则 P =1 时的需求价格弹性是 。 二、计算(6 分×8) 1.计算 ( ) 2 sin 0 lim 1 3 x x x → +

2求位》 3.计算∫x+3x+2 dx 4.设可微函数y=)由方程。=23y确定,试求 的值。 xl=o 第2页共6页
第 2 页 共 6 页 2.求 1 1 1 lim x→ ln 1 x x − − 。 3.计算 4 2 d 3 2 x x x + + 。 4.设可微函数 y y x = ( ) 由方程 e 2 3 x y x y = 确定,试求 0 d d x y x = 的值
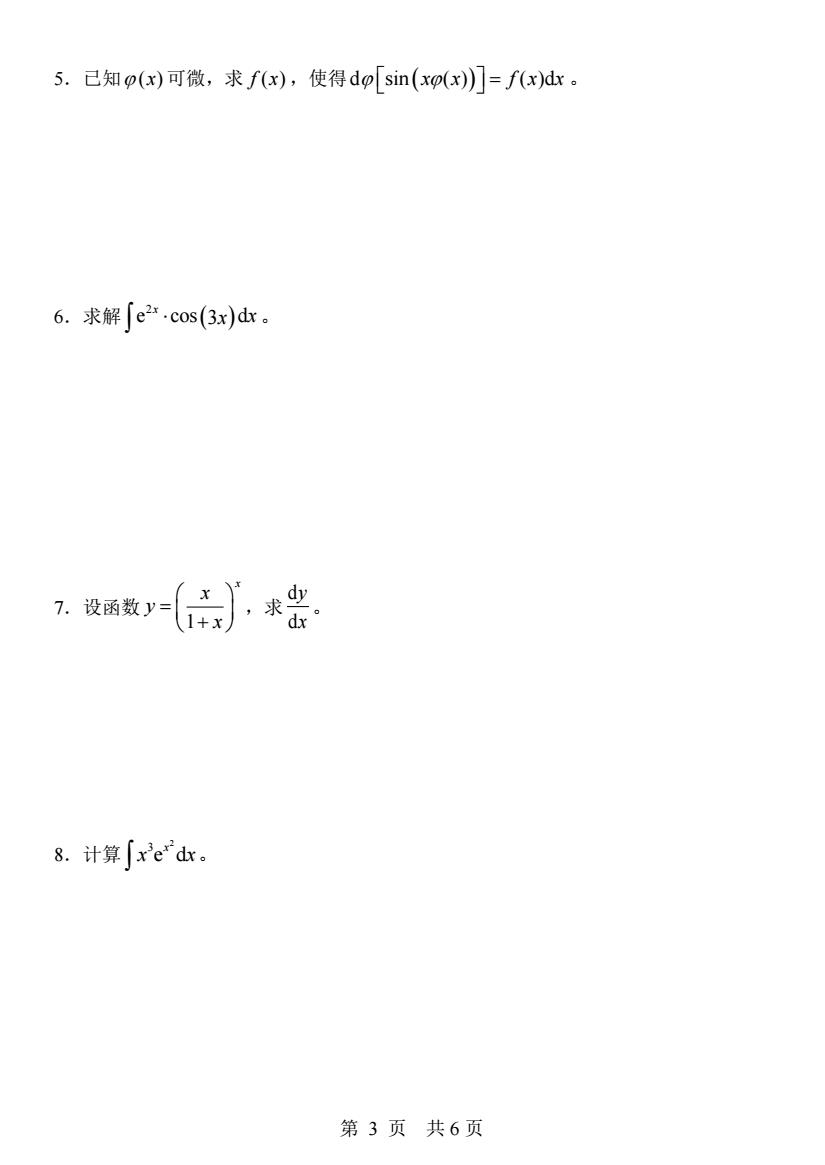
5.已知p(x)可微,求fx),使得do sin(xp(x)]=f(x)dr。 6.求解[e2xcos(3x)dr。 7.设函数y= 8.计算∫xedc。 第3页共6页
第 3 页 共 6 页 5.已知 ( ) x 可微,求 f x( ) ,使得 d sin ( ) ( )d ( x x f x x ) = 。 6.求解 ( ) 2 e cos d 3 x x x 。 7.设函数 1 x x y x = + ,求 d d y x 。 8.计算 2 3 e dx x x

三、解答题(24分) Fx,x≤-1 1.(4分)设函数f(x)= 树 ,-1<x<2 ,x22 确定f(x)的连续区间。若有间断点,判别间断点类型。 2.(5分)求函数f(x)=:按(x-8)的幂展开的带有拉格朗日型余项的2阶泰勒公式。 第4页共6页
第 4 页 共 6 页 三、解答题(24 分) 1.(4 分)设函数 2 , 1 1 ( ) , 1 2 1 , 2 x x f x x x x x − − = − 确定 f x( ) 的连续区间。若有间断点,判别间断点类型。 2.(5 分)求函数 3 f x x ( ) = 按 ( x −8) 的幂展开的带有拉格朗日型余项的 2 阶泰勒公式

3.(10分)列表讨论函数f(x)=e的单调区间、极值、凹凸区间、拐点,并求出其 渐近线。 4.(5分)一商家销售某种商品的价格满足关系式P=7-0.2x(单位:万元/吨),x为 销售量(单位:吨)。商品的成本函数是C(x)=3x+1(单位:万元),若每销售一吨产 品,政府要征税t(万元),试计算: (1)商家获最大利润时的销售量: (2)1为何值时,政府税收总额最大? 第5页共6页
第 5 页 共 6 页 3.(10 分)列表讨论函数 2 ( ) e x f x − = 的单调区间、极值、凹凸区间、拐点,并求出其 渐近线。 4.(5 分)一商家销售某种商品的价格满足关系式 P x = −7 0.2 (单位:万元/吨), x 为 销售量(单位:吨)。商品的成本函数是 C x x ( ) 3 1 = + (单位:万元),若每销售一吨产 品,政府要征税 t (万元),试计算: (1)商家获最大利润时的销售量; (2) t 为何值时,政府税收总额最大?

四、证明题(5分×2) 1.求证当x≤1,时arctanx--h+r)小晋-h2。 A 2.设f(x)在[a,b]上连续,在(a,b)内二阶可导,且f(a=f(b)=0, f"()0(r∈(a,b)。 第6页共6页
第 6 页 共 6 页 四、证明题(5 分×2) 1.求证当 1 1 2 x 时, ( ) 2 arctan ln ln 2 1 4 x x − − + ; 2.设 f x( ) 在 a b, 上连续,在 (a b, ) 内二阶可导,且 f a f ( ) = = (b) 0, f x ''( ) 0 ( x a b ( , )) ,求证: f x( ) 0 ( x a b ( , ))