
北京化工大学2008—2009学年第二学期 《高等数学》(下)期末考试试卷 课程代码MAT13901T 班级: 姓名: 学号: 分数: 题号 二 总分 得分 一、填空(3分×618分) 1.函数z=√n(x)的定义域 2.设=,则份 x2+y2=8 3.曲线 :=F+了在点2,222)处的切线方程 4.设2由不等式x2+y2+:2≤z,z2√2+少所确定,川f(x,y,2)dv在球坐标 系下的三次积分为 5.设方程D(cx-az,cy-bz)=0确定了函数:=f(x,y),(u,)有连续一阶偏 导数,则6x 6.设Σ为曲面x2+y2+22=R的下半部分(2≤0)的上侧,将对坐标的曲面积分 ∬P(x,y,)ddz+O(x,y,)ddx+Rx,y,)dxdy化成对面积的曲面 积分为 第1页
第 1 页 北京化工大学 2008——2009 学年第二学期 《高等数学》(下)期末考试试卷 课程代码 M A T 1 3 9 0 1 T 班级: 姓名: 学号: 分数: 题号 一 二 三 总分 得分 一、填空(3 分×6=18 分) 1.函数 z x y = ln( ) 的定义域 。 2.设 y u zx = ,则 1 1 1 d x y z u = = = = 。 3.曲线 2 2 2 2 x y 8 z x y + = = + 在点 (2 , 2 , 2 2 ) 处的切线方程 。 4.设 由不等式 2 2 2 x y z z + + , 2 2 z x y + 所确定, f x y z v ( , , d) 在球坐标 系下的三次积分为 。 5.设方程 − − = (cx az cy bz , 0 ) 确定了函数 z f x y = ( , ) ,(u v, ) 有连续一阶偏 导数,则 z x = 。 6.设 为曲面 2 2 2 2 x y z R + + = 的下半部分 (z 0) 的上侧,将对坐标的曲面积分 P x y z y z Q x y z z x R x y z x y ( , , d d , , d d , , d d ) ( ) ( ) + + 化成对面积的曲面 积分为
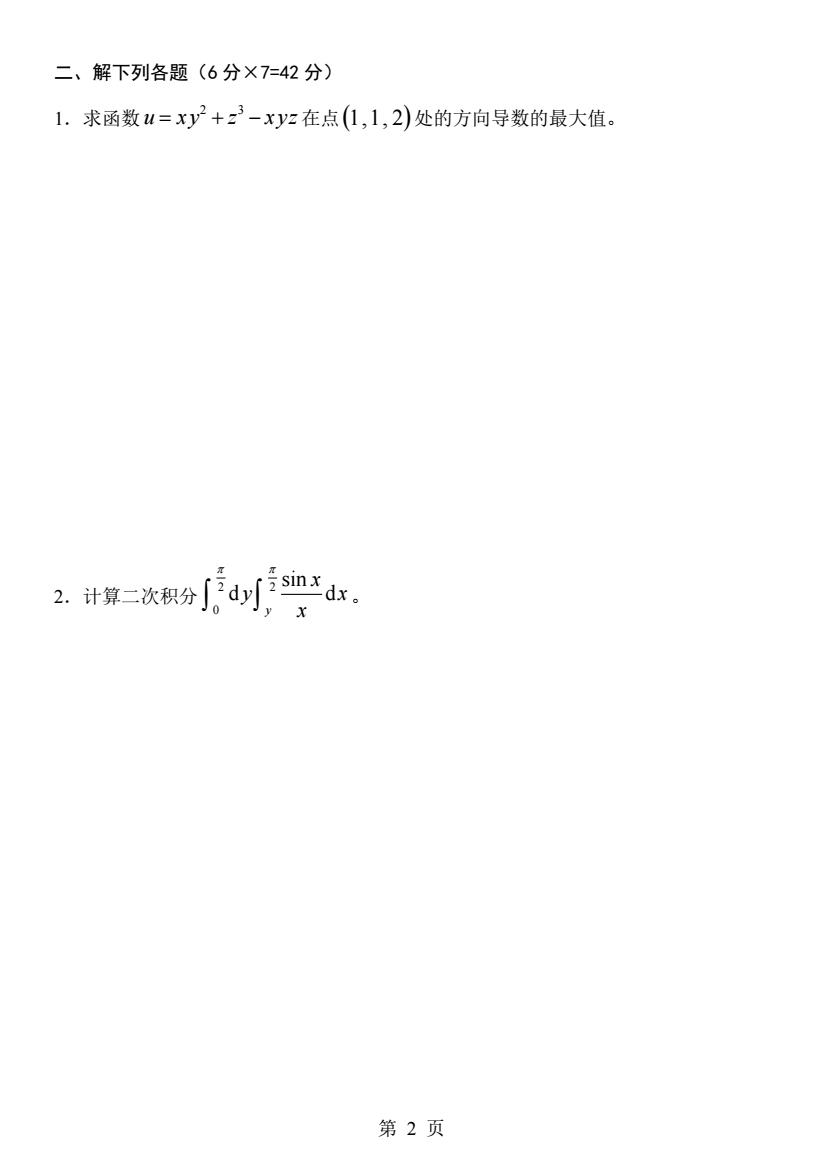
二、解下列各题(6分×7=42分) 1.求函数u=xy+z3-xyz在点(1,1,2)处的方向导数的最大值。 2.计第二次积分dndx。 y x 第2页
第 2 页 二、解下列各题(6 分×7=42 分) 1.求函数 2 3 u x y z x yz = + − 在点 (1,1, 2) 处的方向导数的最大值。 2.计算二次积分 2 2 0 sin d d y x y x x

3.设某种物质的质量在化学反应中随时间变化的速率与该物质当时的质量成正比,若 初始时刻为100克的该物质,在1小时后质量减少为50克,问3小时后该物质还剩多 少克? 4.求曲面z=x2+y被x2+y2+z2=6所截出的有限部分的面积。 第3页
第 3 页 3.设某种物质的质量在化学反应中随时间变化的速率与该物质当时的质量成正比,若 初始时刻为 100 克的该物质,在 1 小时后质量减少为 50 克,问 3 小时后该物质还剩多 少克? 4.求曲面 2 2 z x y = + 被 2 2 2 x y z + + = 6 所截出的有限部分的面积

5.设曲线L:y=x+1(0≤x≤1),L上任一点处的线密度为该点到原点距离的平 方,求曲线L质心的横坐标x。 6.计算三重积分∬d,2由x2+y2+2≤1与+1≥V2+y确定。 第4页
第 4 页 5.设曲线 L : y x = +1 ( 0 1 x ), L 上任一点处的线密度为该点到原点距离的平 方,求曲线 L 质心的横坐标 x 。 6.计算三重积分 z vd , 由 2 2 2 x y z + + 1 与 2 2 z x y + + 1 确定

7.设曲面Σ:2=x2+y2(0≤z≤1),其法向量与:轴正方向夹角为锐角,求 J(2x+z)ddz+zd=dx。 三、解下列各题(8分×5=40分) 1设:=(+少,引了具有=阶选续偏导数,求 第5页
第 5 页 7.设曲面 : 2 2 z x y = + ( 0 1 z ),其法向量与 z 轴正方向夹角为锐角,求 (2 d d d d x z y z z z x ) + + 。 三、解下列各题(8 分×5=40 分) 1.设 2 2 , y z y f x y x = + , f 具有二阶连续偏导数,求 2 z x y

2.求都级数2-广任+的收数装.和晒数。以及数项级数 的和。 后n 第6页
第 6 页 2.求幂级数 ( ) ( ) 2 1 1 1 n n n x n = + − 的收敛域,和函数,以及数项级数 ( ) 1 1 n n n = − 的和

10≤x≤1 3.将函数f(x)= {x+11≤S元在0,网上展成余弦级数,并指出展开式成立的范 围。 4.在平面x+y-4z=1上求一点,使它与点A1,1,1),B(1,0,2)的距离平方之和 最小。 第7页
第 7 页 3.将函数 1 0 1 ( ) 1 1 x f x x x = + 在 0, 上展成余弦级数,并指出展开式成立的范 围。 4.在平面 x y z + − = 4 1 上求一点,使它与点 A(1,1,1), B(1, 0 , 2) 的距离平方之和 最小

5.设函数p(x)二阶可导,p(m)=0,'()=-,曲线积分 ∫e【eosx-odr+p'xdy 与路径无关。 求:(1)p(x)的表达式:(2)从A1,0)到B(π,π)的积分值。 第8页
第 8 页 5.设函数 ( ) x 二阶可导, ( ) 0 = , '( ) 2 = − ,曲线积分 cos ( ) d '( )d AB x x y x x y − + 与路径无关。 求:(1) ( ) x 的表达式;(2)从 A(1, 0) 到 B( , ) 的积分值